TIMSS 2015高中數學評價框架

曾小平+洪小輝

國際數學與科學教育成就趨勢研究（The Trends in International Mathematics and Science Study，簡稱TIMSS），是由國際教育成就評價協會（The International Association for the Evaluation of Educational Achievement，簡稱IEA）組織的大型國際教育評價研究項目.該研究的目的在于，評價各國中小學數學與科學教育成就的發展趨勢，研究各國數學與科學教育成就同文化背景、教育制度等影響因素的關系，幫助各國提升數學和科學教育質量.

TIMSS的數學評價主要針對四年級、八年級和高中階段進行. 其中，首次TIMSS高中數學評價于1995年進行，第二次于2008年進行，第三次將于2015年進行. 2014年3月，國際教育成就評價協會的官方網站上發布了TIMSS 2015高中數學評價框架（TIMSS Advanced 2015 Mathematics Framework[1]）. 下面我們對此框架進行詳細介紹.

一、TIMSS高中數學評價概要

TIMSS認為，高中階段的數學學習應當為大學學習做充分的準備，而大學學習又是為學生將來從事科學、技術、工程和數學等職業做準備的.今天的高中學生，將會成為明天的科學家與工程師，將會成為經濟社會中科學創新與技術發展的重要力量.因此，國家和社會都應該高度關注高中畢業生的數學水平，以確保其為富有挑戰的大學學習做好充分的準備.

因此TIMSS特別針對各國高中數學教育進行評價，主要針對十二年級學生進行.評價框架盡量貼近各參與國家和地區的數學課程標準與教育改革，比如，美國的“共同核心數學標準”（Common Core State Standards for Mathematics[2]，2010）、新加坡的“高中數學教學大綱”（Mathematics Higher 2 Syllabus）、中國香港的“高中數學課程”（Mathematics Curriculum Secondary 4-6）和美國大學理事會的《微積分》（AP Calculus Course Description，2012）.

TIMSS高中數學教育評價重點評價學生數學基礎知識的掌握和數學思考的過程. 評價框架包括“知識”和“認知”兩個領域，“知識領域”（Content Domains）包括代數、微積分和幾何，“認知領域”（Cognitive Domains）包括知道、運用和推理.TIMSS評價結果將有助于各國評價其自身的教育政策與教學策略，優化自身的課程結構，為學生在大學學習科學、技術、工程和數學做好充分準備.

二、評價框架的知識領域

TIMSS 2015高中數學評價框架的“知識領域”包含“代數”、“微積分”和“幾何”三個區域，各區域所占比重分別為35%、35%和30%.

（一）代數

代數是進一步學習數學和其他學科的基礎，包括“表達式與運算”、“方程與不等式”和“函數”三個主題.

1.代數式與運算

進行指數式、對數式、多項式、有理式、無理式的運算，進行復數的運算;對代數式進行評價;算術級數與幾何級數的通項公式，數列的前n項和公式和各項和公式.

2.方程與不等式

求解一元二次方程與不等式;求解指數式、對數式、多項式、有理式和無理式方程;用一元二次方程與不等式解決問題.

3.函數

進行函數的等價表征，比如圖象、文字、公式和復合函數等之間的轉換;識別和比較指數函數、對數函數、多項式函數、有理函數和無理函數的特征.

（二）微積分

微積分是理解物質世界運行原則的重要手段，也是絕大多數以數學為基礎的科學類學科的中心思想.微積分的內容包括極限、微分和積分.重點是極限概念和函數極限、函數的導數與微分，并用這些技能解決問題.

1.極限

求函數的極限（包括無理函數）;確定和描述函數連續與可導的條件.

2.微分

求多項式函數、指數函數、對數函數、三角函數、有理函數、無理函數和復合函數的導數，積與商的導數;利用導數解決最優化和變化率問題;利用一次和二次導數來確定斜率、極值和多項式函數與有理函數的拐點;使用一次和二次導數來繪制和描述函數圖象.

3.積分

求多項式函數、指數函數、三角函數和簡單無理函數的積分;計算定積分，并利用積分來求面積與體積.

（三）幾何

幾何被直接用于解決許多現實問題，被廣泛用于科學中.同時，源于研究測量問題的三角學，也是幾何學的重要元素.幾何包括坐標幾何與非坐標幾何和三角學兩個板塊.

1.坐標幾何與非坐標幾何

利用非坐標幾何解決平面和立體圖形的問題;用坐標幾何解決平面幾何問題;使用向量解決幾何問題.

2.三角學

使用三角學解決涉及三角形的問題;識別、描述和繪制正弦、余弦和正切函數的圖象.

三、評價框架的認知領域

TIMSS 2015高中數學評價的“認知領域”包含“知道”、“運用”和“推理”三個區域，各區域所占比重分別為35%、35%和30%.

（一）知道

“知道”是指學生需要知道的數學事實、概念和程序.該區域包含“回憶”、“辨認”、“計算”和“提取”四個層級，各層級的含義見表1.

表1 “知道”的四個層級

（二）運用

“應用”區域，著重于評價學生運用知識和概念的理解來創造表征和解決問題的能力.問題可能來源于現實生活，也可能來源于數學內部，比如數字或代數表達式、函數、方程和幾何圖形.該區域包含“確定”、“表征、建模”和“實施”三個層級，各層級的含義見表2.endprint

表2 “運用”的三個層級

（三）推理

“推理”需要邏輯性和系統性思維.推理包括形成猜想、基于預先假設與已有規則進行邏輯演繹推理和證明結果.該區域包括“分析”、“整合、綜合”、“評價”、“結論”、“概括”和“辯護”六個層級，各層級的含義見表3.

表3 “推理”的六個層級

四、高中數學的評價樣題

在TIMSS 2015評價框架的“附錄”中，給出了一些評價樣題.通過這些樣題，我們可以更好地了解TIMSS 2015高中數學評價的形式、理念與重點.

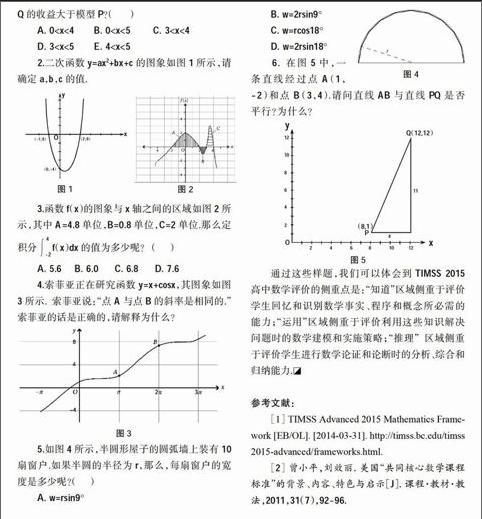
1.下面兩個函數模型預測了收益y（美元）與銷量x（千件）之間的關系，其中x的范圍是0

A. 0

D. 3

2.二次函數y=ax2+bx+c的圖象如圖1所示，請確定a，b，c的值.

3.函數f（x）的圖象與x軸之間的區域如圖2所示，其中A=4.8單位，B=0.8單位，C=2單位.那么定積分f（x）dx的值為多少呢？ ?（ ? ?）

A. 5.6 ? ?B. 6.0 ? ? C. 6.8 ? ? D. 7.6

4.索菲亞正在研究函數y=x+cosx，其圖象如圖3所示.索菲亞說：“點A與點B的斜率是相同的.”索菲亞的話是正確的，請解釋為什么？

5.如圖4所示，半圓形屋子的圓弧墻上裝有10扇窗戶.如果半圓的半徑為r，那么，每扇窗戶的寬度是多少呢？（ ? ?）

A. w=rsin9°

B. w=2rsin9°

C. w=rcos18°

D. w=2rsin18°

6.在圖5中，一條直線經過點A（1，-2）和點B（3，4）.請問直線AB與直線PQ是否平行？為什么？

通過這些樣題，我們可以體會到TIMSS 2015高中數學評價的側重點是：“知道”區域側重于評價學生回憶和識別數學事實、程序和概念所必需的能力;“運用”區域側重于評價利用這些知識解決問題時的數學建模和實施策略;“推理”區域側重于評價學生進行數學論證和論斷時的分析、綜合和歸納能力.

參考文獻：

[1] TIMSS Advanced 2015 Mathematics Framework [EB/OL]. [2014-03-31]. http：//timss.bc.edu/timss

2015-advanced/frameworks.html.

[2] 曾小平，劉效麗. 美國“共同核心數學課程標準”的背景、內容、特色與啟示[J]. 課程·教材·教法，2011，31（7），92-96.