基于降階ESO的電動舵機非奇異終端滑模控制
(北京理工大學 宇航學院,北京 100081)
線性比例電動舵機是導彈、無人機等飛行器的飛行控制系統中重要的組成部件,同時也是高精度位置跟蹤伺服系統。電動舵機的負載會隨著飛行條件的變化而變化,呈現出強時變的特性[1]。舵機系統內部摩擦和間隙是影響舵機系統靜、動態性能的重要因素[2],其非線性特性將導致系統跟蹤誤差增大,嚴重制約了舵機控制系統性能的提高。因此,必須采用適當的補償方法抑制系統內部參數時變和外部負載擾動的影響,以提高系統的跟蹤性能。
通過2種途徑可以提高電動舵機系統的抗干擾能力:一種是從反饋控制器的角度,設計非奇異終端滑模控制器,系統將在有限時間內穩定,特別是在平衡點具有更好的收斂性能且不抖振;另一種是從前饋主動補償的角度,設計觀測器將干擾直接觀測出來,并進行前饋補償。文獻[3]采用自適應非奇異終端滑模實現對電動舵機的控制,收斂性能較好,但只能估計出有界的參數攝動;文獻[4-5]采用擴張狀態觀測器ESO觀測系統狀態及外部干擾,獲得了良好的跟蹤性能,但未提高跟蹤誤差的收斂速度。
本文將降階ESO前饋補償和非奇異終端滑模控制相結合,應用在線性電動舵機的控制中。不僅提高了系統的抗擾動能力,并實現了電動舵機的角度穩定控制和跟蹤誤差的有限時間收斂,提高了系統的動態性能。
1 電動舵機的模型
由于彈上空間和沖擊過載的限制,線性電動舵機采用如圖1所示的傳動機構。同時,電動舵機一般由直流無刷電機、傳動機構、位置傳感器、驅動器和控制器組成。
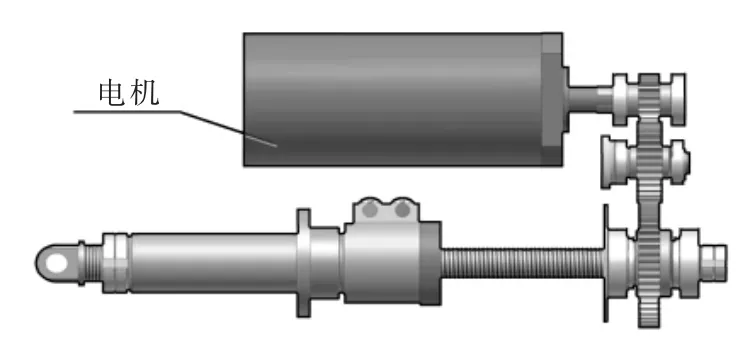
圖1 電動舵機傳動機構Fig.1 Structure diagram of EMA
電動舵機力矩平衡方程為
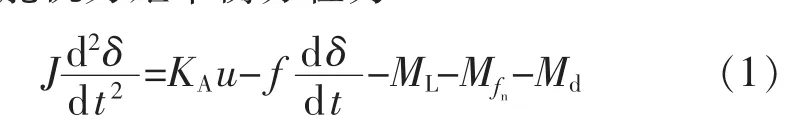
式中:J,f,KA分別為系統等效到舵機輸出軸的轉動慣量、系統總的阻尼系數、力矩系數;ML,Mfn分別為負載力矩、非線性摩擦力矩;Md為系統總的干擾力矩;δ為舵偏角。
系統負載力矩中包括彈性負載和常值負載:

系統中的非線性摩擦力矩Mfn可以采用Stribeck模型描述,在這里采用連續函數去逼近[6]:
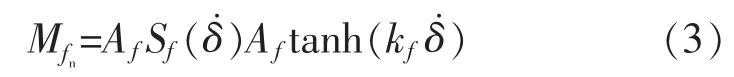
式中:kf>0,當kf足夠大時能以足夠高的精度逼近Mfn。
對模型進行變換,令x1=δ,x2=δ˙,則由式(1)~式
(3)可得:
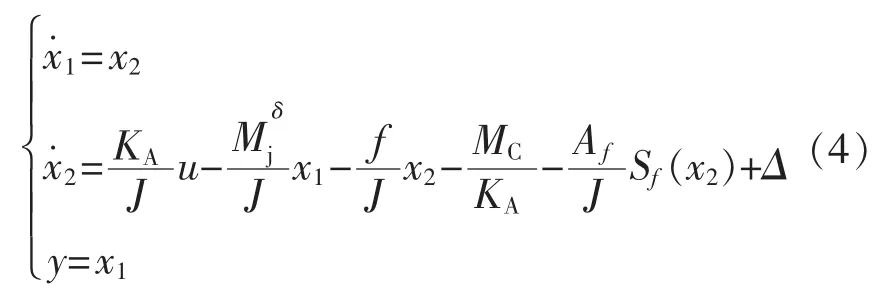
式中:Δ為系統干擾及未建模動態。
將式(4)轉換為如下的標準形式:
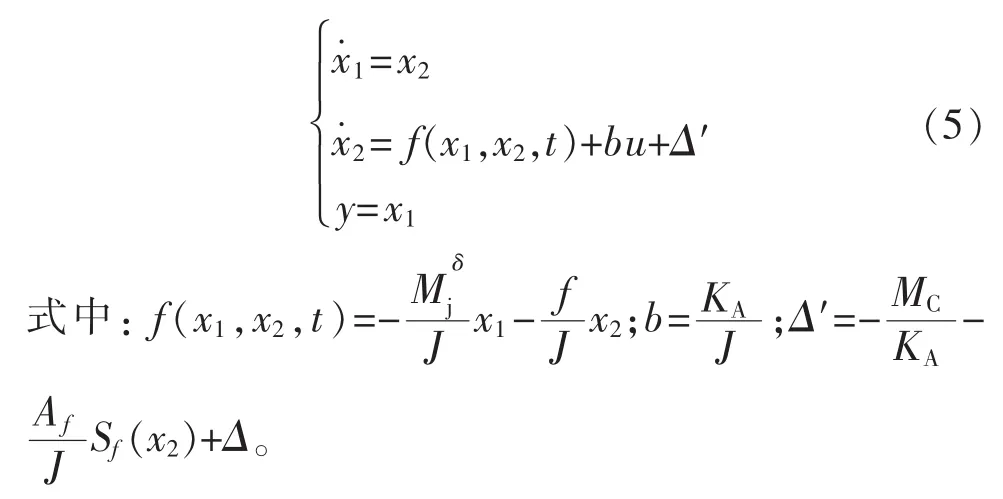
本文研究的問題為設計一個控制器,使得系統(4)的輸出y對有界期望軌跡xd的跟蹤誤差有限時間收斂,并實現對外部干擾及未建模動態的實時估計。
2 復合控制器的設計
2.1 非奇異終端滑模控制器設計
定義系統的跟蹤位置誤差和速度誤差分別為e1
設計如下的滑模面為
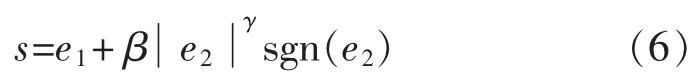
對式(5)求導可得:
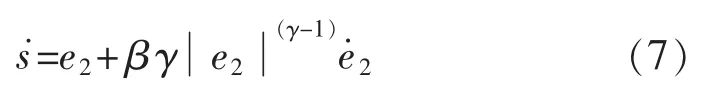
根據如下滑模到達條件:

選取如下的趨近律:
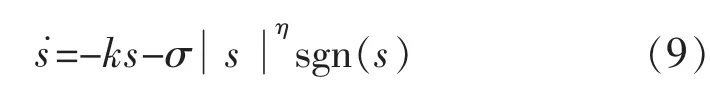
式中:k>0,σ>0,0<η<1。該趨近律能夠保證系統(4)的跟蹤誤差以有限時間收斂到滑模面s的鄰域內。
由式(5)、(7)和(9)可以知控制律為

由式(10)可以看出:負載力矩、慣性擾動、摩擦阻尼和未建模動態所造成的擾動都可以在d(t)中得到體現。把擾動觀測出來并加以補償后,電動舵機系統就變為二階積分串聯系統。因此,如何快速估算出d(t)的值是控制器設計的關鍵。
2.2 降階ESO的設計
根據文獻[7]提出的線性擴張觀測器LESO的思想,由于x1可以直接測量,可以采用如下形式的降階ESO估計出式(5)中干擾及不確定項:
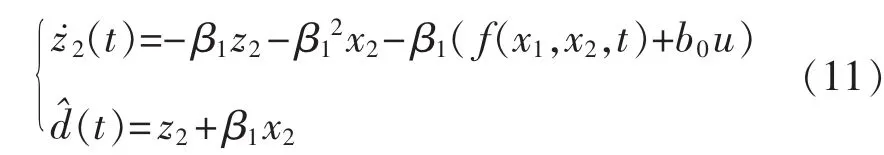
式中:β1為觀測器的增益,可以采用帶寬配置的方法選擇觀測器增益;b0為b的估計值。
上述觀測器可以看作為基于模型的降階ESO,當把系統模型f(x1,x2,t)和Δ′看作系統的總干擾時,降階ESO的形式和文獻[8]是一致的。
此時,將系統“總干擾”估計值代入控制量(10)中可得:
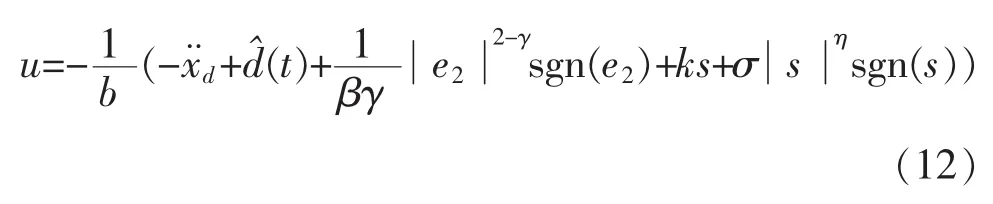
3 閉環系統穩定性分析
為了說明閉環系統的穩定性,首先給出如下的假設和定理。
假設1假設d(t)是有界的并存在一個常數M>0,則有:

定理1若假設1滿足,且合理選取觀測器增益β1,那么觀測器誤差e0指數收斂并有界,且收斂域為[8]
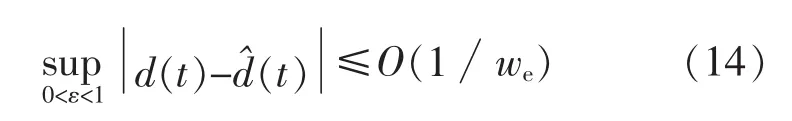
式中:we為觀測器帶寬。
接下來考慮在降階ESO(11),滑模面(6)與控制律(12)作用下的閉環系統的收斂特性。
針對系統(5)構造如下的正定Lyapunov函數:

對式(15)按時間t求導可得:
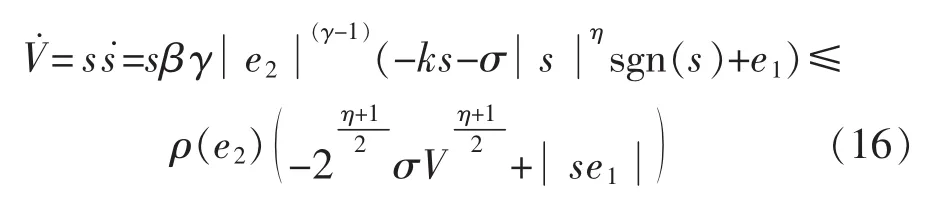
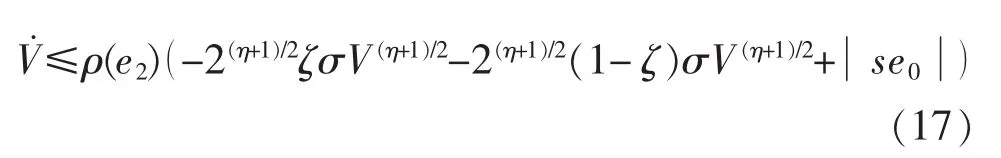

式中:0<ζ0<1。同時,有限收斂時間可以表示為
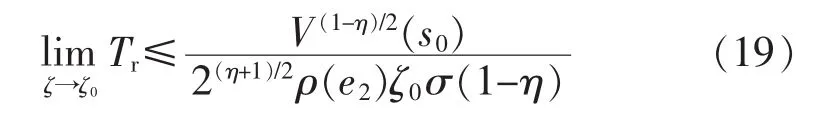
綜上所述,在觀測器穩定的前提下,通過調節控制律(12)中的參數k,σ,可以保證系統的軌跡有限時間收斂于s=0的鄰域p內,即狀態量x1將在有限時間內跟蹤上期望值x1d,但是存在穩態收斂誤差。穩態收斂誤差的收斂域與系統觀測器的觀測誤差成正比。但是,觀測器的帶寬將增大,引入的觀測噪聲會降低觀測器的估計能力,應合理的選取觀測器及控制器參數。
4 仿真結果與分析
為了驗證所提電動舵機復合控制方法的有效性,對2種控制方法:自適應非奇異終端滑模控制(CANTSMC)和基于降階ESO的非奇異終端滑模控制(TSMC+RESO)在電動舵機系統的應用做仿真比較。仿真時電動舵機的參數為Nm/rad;Mc=4.12 Nm;f=9.12 Nm(rad/s)-1;KA=28.23 Nm/V,系統干擾可以表示為
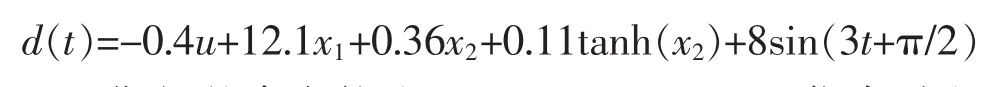
期望的參考軌跡x1d=0.2sin(2πt)rad,仿真時電流限幅-20 A~20 A,采用ODE4仿真算法,仿真時長為10 s,仿真步長為0.001 s。控制器參數分別為
1)CANTSMC控制器參數為

2)TSMC+RESO控制器參數為

采用TSMC+RESO控制方法時電動舵機舵偏角跟蹤曲線如圖2所示。由圖2可知,系統舵偏角輸出具有良好的跟蹤性能,同時具有良好的抗干擾能力。
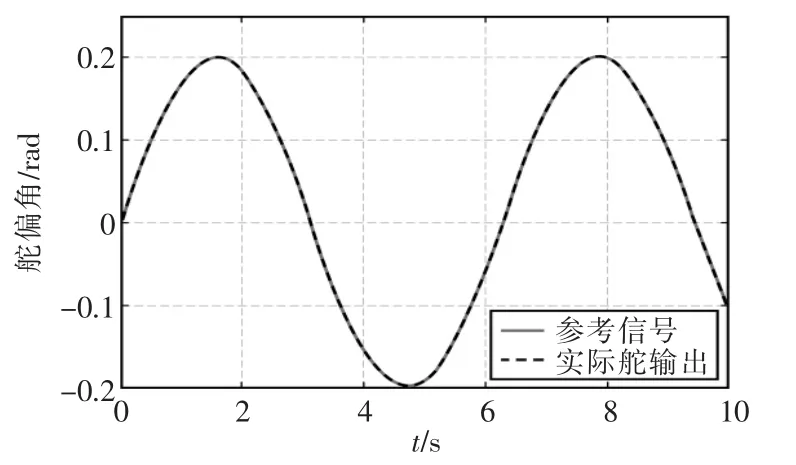
圖2 舵偏角跟蹤曲線Fig.2 Output x1follows desired trajectory yd
同時2種控制方法對比,舵偏角跟蹤誤差曲線如圖3所示。由圖3可知,本文提出的控制方法具有更小的跟蹤誤差,且誤差收斂速度接近。但是,采用觀測器估計系統不確定性,進一步降低了控制器設計的保守性,并減少了控制參數。在圖4中,TSMC+RESO具有更小的控制量,同時消除了抖振。
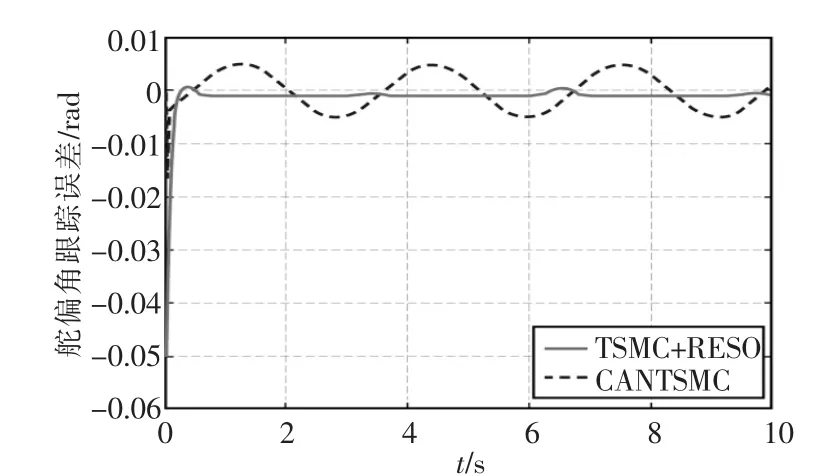
圖3 系統跟蹤誤差曲線Fig.3 Tracking error of the system
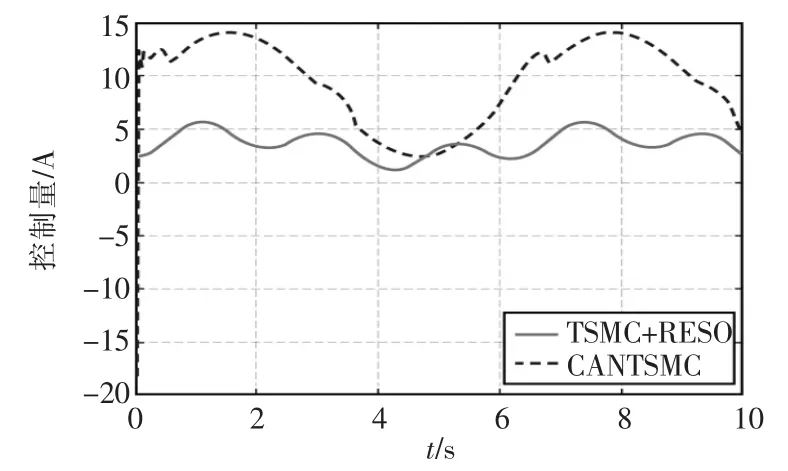
圖4 系統輸出控制量曲線Fig.4 Control effort of the system
根據文獻[3]中的定義和方法,采用自適應方法估計系統參數的攝動,而本文采用觀測器不僅估計了系統內部的參數攝動,同時也估計了系統的干擾以及未建模動態。下面考察觀測器的估計能力,觀測器增益β分別為10和20,觀測器的觀測誤差曲線如圖5所示。
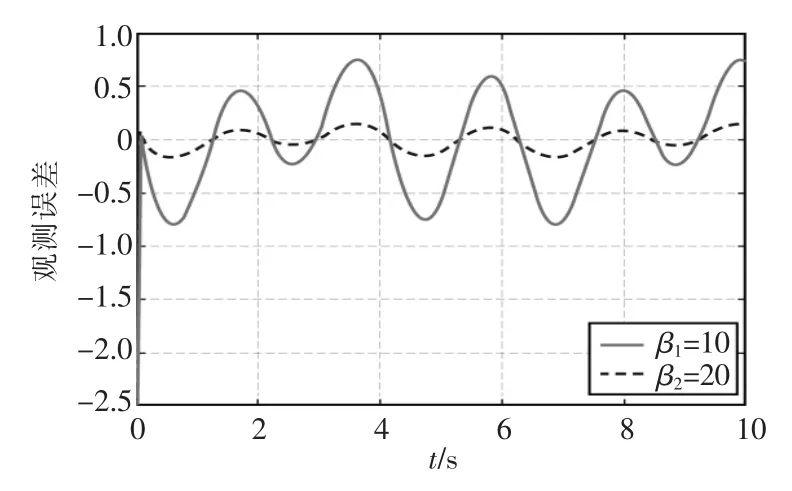
圖5 觀測器觀測誤差曲線Fig.5 Estimated error of the RESO
由圖5可知,隨著觀測增益的增大,觀測誤差減小,與定理1中的結論是一致的。同時,觀測器的增益不能任意增大,當觀測器增益增大會引入觀測器噪聲,降低觀測器的性能。
5 結語
本文針對線性電動舵機的精確跟蹤問題,設計了基于降階ESO的非奇異終端滑模控制方法。首先,降階ESO用來估計系統“總干擾”,并將估計值主動補償到輸入端;其次,非奇異終端滑模控制保證系統跟蹤誤差有限時間收斂。此外,對閉環系統的穩定性進行了分析,給出了誤差收斂域,為控制參數選取提供了理論參考。最后,通過對比仿真驗證了該方法的有效性。
[1] 吳森堂,費玉華.飛行控制系統[M].北京:北京航空航天大學出版社,2005.
[2] 彭書華,李華德,蘇中.非線性摩擦干擾下的電動舵機滑模變結構控制[J].信息與控制,2008,37(5):127-130.
[3] 李浩,竇麗華,蘇中.電動舵機的復合自適應非奇異終端滑模控制[J].控制理論與應用,2011,28(8):75-79.
[4] 夏長亮,劉均華,俞衛,等.基于擴張狀態觀測器的永磁無刷直流電機滑模變結構控制[J].中國電機工程學報,2006,26(20):139-143.
[5] 熊官送,那學智,曹東海.自抗擾控制技術在電動舵系統中的應用[J].導航定位與授時,2014,1(3):42-46.
[6] H.Olsson,K.J.Astrom,et al.Friction models and friction compensation[J].European Journal of Control,1999,10(2):1243-1254.
[7] Gao Z Q.Scaling and bandwidth-parameterization based controller-tuning[C]//Proceedings of the 2003 American Control Conference,Denver,IEEE 2003:4989-4996.
[8] 薛文超.自抗擾控制的理論研究[D].北京:中國科學院數學與系統科學研究院,2012.

