基于位置測量的機電系統(tǒng)建模及其控制

杜紅彬，康小明，楊克濁

（華東理工大學 自動化系，上海200237）

機電運動系統(tǒng)常常是受未知轉(zhuǎn)動慣量和摩擦力影響的非線性系統(tǒng)。在高精度的機電運動控制中，控制超調(diào)通常會引起不必要的調(diào)節(jié)誤差，特別是在軌跡跟蹤的控制要求中[1]，超調(diào)引起的調(diào)節(jié)誤差不僅會對跟蹤精度造成很大的破壞，同時也會浪費控制能量。因此，為了提高跟蹤的精度以及抗干擾能力，在設(shè)計前饋控制器或干擾估計器[1-2]之前，往往需要辨識出比較準確的模型參數(shù)[3-4]。但是在實際應用中，速度的測量通常是通過編碼器的定時后向差分[4]來獲得的，如何選擇合適的采樣周期來實現(xiàn)差分測速是一個很棘手的問題。若定時采樣周期太小，就有可能出現(xiàn)編碼器差分為零的情況，或速度變化緩慢，不能反映快速的速度變化；若定時采樣周期太大，就可能出現(xiàn)編碼器差分過大，速度變化劇烈，從而漏掉某些低速的變化信息。不僅辨識，控制器設(shè)計往往也需要速度測量。由于后向差分的這種缺點，勢必會對辨識和控制造成一定的誤差。

針對上述問題，并根據(jù)摩擦力具有局部性非線性的特點，本文提出了一種新穎的辨識方法來解決上述難點，該方法能夠快速地完成辨識計算，而且僅需要位置反饋而不需要速度測量。同時設(shè)計了動態(tài)尺度化觀測器及相應的輸出反饋控制器，以避免上述分析中的差分誤差，并證明了閉環(huán)系統(tǒng)的穩(wěn)定性。

1 運動系統(tǒng)模型及辨識算法

由于電磁轉(zhuǎn)換時間常數(shù)非常小，因此可將單自由度機電運動控制系統(tǒng)表達為

其中：m為未知的轉(zhuǎn)動慣量；p為位置；v為轉(zhuǎn)速；u為控制輸入；b為未知的控制增益；f（v）為摩擦力。如果考慮用機理模型表達摩擦力，通常采用Lugre模型[7]：

其中：σ0～σ1，a0～a2，v0是待定的參數(shù)。

盡管在文獻中基于Lugre的模型常常被采用，但是這類機理模型存在著以下缺陷使得其實際應用并不理想：

1）機理模型中有許多待定的參數(shù)，并且很難估計這些參數(shù)值。

2）在模型（2）中采用動態(tài)方程描述摩擦力，其中的狀態(tài)變量無法直接測得。

3）摩擦力模型往往只針對在特定的實驗條件，而這些條件不具備普適性。

近來，一些學者采用神經(jīng)網(wǎng)絡(luò)等逼近的方法對摩擦力建模[4-5]，而文獻[6]提出用3個正切神經(jīng)元基函數(shù)靜態(tài)描述摩擦力的非線性現(xiàn)象，摩擦力模型給出如下：

其中：靜摩擦力系數(shù)是 r1，r4，r6；Stribeck 現(xiàn)象由 tanh（r2v）-tanh（r3h）表示；Coulomb 摩擦力是由 r4tanh（r5v）表示；Viscous摩擦力是由r6v表示。注意在文獻[7]中，Coulomb摩擦力一般表達為符號函數(shù)，即：r4sgn（v）表達式。

用符號函數(shù)表達Coulomb摩擦力的缺點是：其不連續(xù)性會導致最終設(shè)計的控制器不連續(xù)。為了消除不連續(xù)性，可以用光滑的雙曲正切函數(shù)tanh（·）來替代符號函數(shù) sgn（·）。

將式（4）替代式（1）中的 Lugre 摩擦力模型，并且兩邊同時除以b，即：

式中：m，b，r1～r6都是未知的參數(shù)；tanh（r5v）=sgn（v）。

為了能有效地辨識出式（5）中的未知參數(shù)，可以看到式（4）中的Stribeck現(xiàn)象具有局部性的特點。簡單地說，摩擦力的非線性現(xiàn)象在低速時表現(xiàn)為Stribeck現(xiàn)象，而當速度v大于一個特定的速度v*時，摩擦力的非線性現(xiàn)象消失為0，根據(jù)以上情況，可以設(shè)想：當用適當大的控制輸入使得速度由0變大，并保證速度大于Stribeck區(qū)的閾值v*（該閾值對應著時間t*），使得摩擦力非線性現(xiàn)象消失，當t≥t*時，有如下公式成立：

常數(shù)k5是由于Stribeck現(xiàn)象的局部性產(chǎn)生的；由于直接利用編碼器測量出的速度值會存在一定的差分誤差，因此直接用來進行辨識會造成辨識參數(shù)值不準確，而事實上編碼器測出位置的準確度通常比速度測量的準確度要高很多，并且不容易受采樣周期選擇的困擾，所以如果能夠利用位置測量值來完成辨識顯然會提高辨識的質(zhì)量。基于此，對式（6）兩邊再進行積分，并且假設(shè)控制電機朝單個方向運動，即速度為正，有：

定義：

由式（8）及

可以得到：

這樣，應用最小二乘可計算出θ估計值：

但最小二乘的缺點是：當N選得很大時，式（10）的計算量太大，通常會出現(xiàn)過擬合問題而且需要離線計算才能獲得，也不利于在芯片上在線實施。針對系統(tǒng)（5），求解式（10）最小的N定為4個一定時間間隔的數(shù)據(jù)點，即：

上邊的式子中含有4個未知參數(shù)對應4個方程。這樣在保證最少是4個點的采樣數(shù)據(jù)下，可采用全主元高斯消去法快速求出4個未知參數(shù)值，從而簡化了計算量并大大節(jié)省了計算時間。為保證上述4個方程有解，4個控制輸入應該互不相同。通常采用不同的控制輸入來獲得不同的速度值，這也是辨識中常見的持續(xù)激勵PE（persistently exciting）條件的要求[8]。例如，可采用斜坡函數(shù)作為控制輸入來激發(fā)系統(tǒng)，這樣容易獲得4個不同的速度值。為方便于實際使用，在此舉例對辨識過程進行詳細地說明。控制輸入采用斜坡函數(shù)作為激勵信號，令u=k1+k2t，由式（7）并且離散化得到結(jié)果，在實施中，由于使用定時中斷實現(xiàn)采樣周期，采樣周期可單位化，即 Ts=1。 根據(jù)式（7）得到離散化結(jié)果，式（11）也可離散化，值得說明的是，盡管上述辨識方法能直接辨識出未知參數(shù)但式（4）中的參數(shù) r1～r3仍然是未知的，因此接下來將在控制器設(shè)計中對這些未知參數(shù)進行自適應補償。

2 基于動態(tài)尺度化觀測器的輸出反饋設(shè)計及閉環(huán)穩(wěn)定性分析

一般來說，速度通過定時后向差分獲得，常見的有M法、T法或M/T法測量速度。這些方法要么是對低速或高速測量有效，要么就是實現(xiàn)起來非常困難，因此很難滿足高精度控制算法的要求。受文獻[9]啟發(fā)，本文提出采用動態(tài)尺度化的高增益觀測器來對速度進行估計，以提高速度估計的精度。假設(shè)要跟蹤的位置、速度和加速度曲線分別是：pr，vr=

則跟蹤誤差為e1=p-pr，e2=v-vr

動態(tài)跟蹤系統(tǒng)變成為

采用如下動態(tài)尺度化的高增益觀測器和控制器：

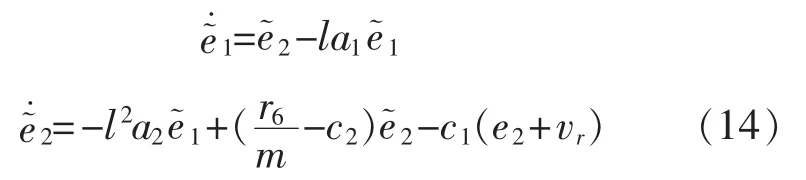
考慮下面的坐標尺度變換：

由式（13）、式（14）可以整理成以下矩陣形式：

可以選擇合適的參數(shù)使得矩陣滿足如下關(guān)系：

定義常數(shù) m0=‖PkC1‖2，m1=‖PaC2‖2，m2=‖PaC3‖2，m3=‖PaC4‖2，。 下面給出主要結(jié)論。

定理1 考慮跟蹤系統(tǒng)（12），若采用動態(tài)尺度化的高增益觀測器和控制器（13），則閉環(huán)系統(tǒng)收斂且有界的。

證明：

考慮如下Lyapunov函數(shù)：

對式（18）求導并且利用不等式關(guān)系可以得到：

對式（19）積分得到：

對式（20）兩邊除以t，并對兩邊求極限并根據(jù)洛比達法則得到：

3 仿真

采用常見的Lugre模型來驗證本文提出的辨識和控制算法，模型如式（1）～（3）所示，其中 m=0.0022（kg·m-2），b=0.152，摩擦力模型的參數(shù)如下（參數(shù)意義見參考文獻[5]）。

為了保證在4個不同的時刻分別獲得4個不同的速度值，辨識采用時間的斜坡函數(shù)，即u=18t，對應式（11），辨識的結(jié)果如下：

為了驗證辨識的效果，將上面的參數(shù)代入到觀測器和控制器中，式（13），其中參數(shù)為

要設(shè)定跟蹤的軌跡為

仿真結(jié)果如圖1所示。

圖1 實際位置和期望位置Fig.1 Actual position and anticipant position

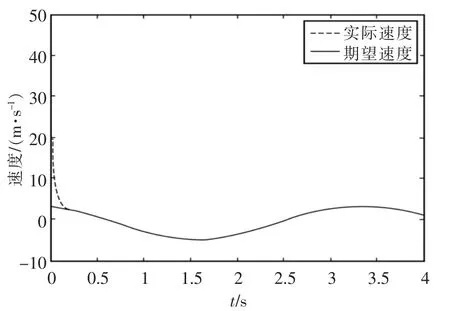
圖2 實際速度和期望速度Fig.2 Actual velocity and anticipant velocity

4 結(jié)語

機電運動系統(tǒng)常常是受未知轉(zhuǎn)動慣量和摩擦力影響的非線性系統(tǒng)，如何對這類系統(tǒng)進行快速準確的建模是當前研究的一個難點。另外，在實際應用中，電機的轉(zhuǎn)速測量通常是通過編碼器的定時后向差分來獲得的，如何選擇合適的采樣周期來實現(xiàn)差分測速常常是一個很棘手的問題。本文針對摩擦力局部性的特點，提出了一種新穎的基于位置測量的快速辨識算法，并設(shè)計了基于動態(tài)尺度化的觀測器的輸出反饋控制，證明了閉環(huán)系統(tǒng)的收斂性。從仿真結(jié)果可以看出，本方法具有良好的性能。

[1]Tomizuka M.Zero phase error tracking algorithm for digital control[J].Journal of Dynamic Systems Measurement and Control—Transactions of the ASME，1987，109：65-68.

[2]Lee HS，Tomizuka M.Robust motion controller design for highaccuracy positioning systems[J].IEEE Transactions on Industrial Electronics，1996，43（1）：48-55.

[3]Kim SJ，Ha IJ.A frequency-domain approach to the identification ofmechanicalsystems[J].IEEE Transactionson Automatic Control，2001，46：888-893.

[4]Selmic RR，Lewis FL.Neural-network approximation of piecewise continuousfunctions：application to friction compensation[J].IEEE Transactions on Neural Networks，2002，13（3）：745-751.

[5]Canudas de Wit C，Olsson H，Astrom KJ，et al.A new model for control of systems with friction[J].IEEE Transactions on Automatic Control，1995，40：419-425.

[6]Makkar C，Hu G，Sawyer WG，et al.Lyapunov-based tracking control in the presence of uncertain nonlinear parameterizable friction[J].IEEE Transactions on Automatic Control，2007，52（10）：1988-1994.

[7]Bona B，Indri M.Friction compensation in robotics：an overview[C]//44th IEEE Conference on Decision and Controland European Control Conference，2005：4360-4367.

[8]Ljung L.System Identification：Theory for the User[M].2nd ed.Englewood Cliffs，N J：Prentice-Hall，1999.

[9]Lei H，Lin W.Universal adaptive control of nonlinear systems with unknown growth rate by output feedback[J].Automatica，2006，42：1783-1789.