帶泊松跳分數市場的歐式冪期權定價

易小蘭，張慶華，閆理坦

（東華大學理學院，上海201620）

帶泊松跳分數市場的歐式冪期權定價

易小蘭，張慶華，閆理坦*

（東華大學理學院，上海201620）

假設標的股票價格服從分數布朗運動環境下帶泊松跳的過程，通過測度變換的方法，選取不同的概率測度，給出冪式期權一種定價公式。

分數布朗運動；泊松跳過程；歐式冪式期權

期權定價問題是金融工程中一個重要的問題，多年來諸多學者對此問題進行了研究。其中最為著名的是1973年Black-Scholes公式，而后期權定價的研究便是在此基礎上作出推廣。該公式有一個很重要的前提條件：原生資產價格演化遵循布朗運動。但是，隨著近年來學者們研究發現，金融資產收益的分布具有“尖峰厚尾”的特征，且股價變化也不是隨機游走，而是不同時間呈現不同程度的長期相關性和自相似性，即未來某時刻股票的價格不僅與現在價格有關，還與過去相當一段時間的價格有關。這些特征與標準的布朗運動存在一定的差距，而分數布朗運動正好具備這些特征。因此，以更為一般的分數布朗運動代替標準布朗運動來進行期權定價問題的研究已成為當前研究的一個主要方向。

近年來，分數布朗運動環境下期權的定價，國內外的學者已經進行了廣泛的研究。其中2003年Hu和B.?ksenda[1]仿照傳統的期權定價的鞅方法理論，建立了關于分數白噪聲的理論體系，證明了分數布朗運動的等價鞅測度定理，并用等價鞅方法得出了歐式看漲期權公式。并證明了基于Wick乘積和白噪聲分析的分數型It?積分下，分數布朗運動市場不存在套利。2004年，劉韶躍，楊向群[2]在標的資產價格服從幾何分數布朗運動且有紅利支付下的假設下，給出了歐式雙向期權定價公式。同年11月，劉韶躍，楊向群在相同的模型下給出了歐式未定權益的一般定價公式及幾種奇異期權的年定價公式。

2007年，趙佃立[3]討論了標的資產受多個分數布朗運動影響的歐式冪期權定價問題。基于風險中性測度，給出了在有紅利支付下且無風險利率及紅利率為隨機函數的情況下的兩類歐式冪期權定價公式。筆者在此基礎上做進一步的研究。

1 理論準備

1.1 分數布朗運動

定義1若一連續的高斯過程稱為分數布朗運動，須滿足以下條件：

（1）BH（0）=0；

（2）EBH（t）=0，t∈R；

（3）EBH（t）BH（s）=（1/2）（|t|2H+|s|2H-|t-s|2H）。

分數布朗運動具有如下性質：

（1）EBH（t）=0，?t≥0；

（2）當H=1時，有BH（t）=B1（t）=tξ，其中ξ是標準正態隨機變量；

（3）BH具有平穩增量：對于s＞0，隨機過程{BH（t+s）-BH（t），t≥0}與隨機過程{BH（t），t≥0}有相同的有限維分布；

（4）軌道連續性：對α＜H，BH有幾乎處處α-階H?lder連續的樣本軌道；

（5）時齊性：對任意s＞0，{BH（t+s）-BH（t），t≥0}也是指標為H的分數布朗運動；

（6）對稱性：隨機過程{-BH（t），t≥0}也是指標為H的分數布朗運動；

（7）自相似性：對任意α＞0，BH（αt）與αHBH（t）有相同的有限維分布；

（8）長期依賴性：H＞1/2時，且當r（n）=cov（BH（1），BH（n+1）-BH（n）），則有；

（9）當H≠1/2時，分數布朗運動既不是半鞅也不是Markov過程。

下面給出分數布朗運動積分的積分表現。

分數布朗運動{BH（t），t≥0}可表示成隨機積分

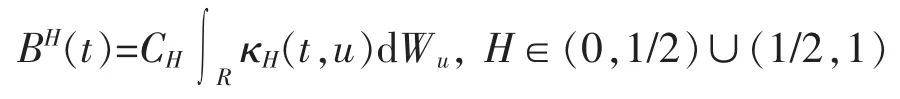
1.2 Wick-It?積分

關于分數布朗運動的積分有軌道積分、Wick積分、散度積分等，但Y.Hu和B.?ksendal在文獻[1]中已證明了不帶跳時，Wick積分應用到金融市場模型時是完備且無套利的，該節主要介紹此種積分[4，5]。

先引進一個分數核函數φ：R2→R，其定義如下

定義2（f范數）設f：R→R是可測的。如果

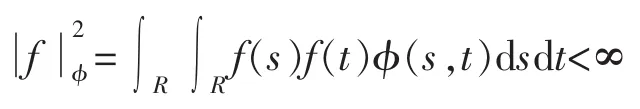
下面介紹Wick積，為了行文簡潔對于下列定義、定理不再證明。

首先，引進Hermite多項式

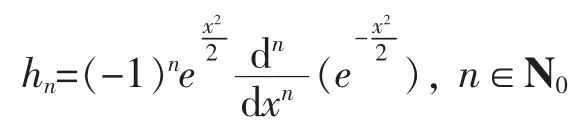
定理1設L∈L2（P），則存在唯一的一組常數cα∈R，其中α∈I，使得

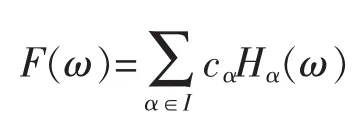
下面介紹兩個對偶空間：

（2）F∈S*，對于F的負范數。對于，定義。

有了以上準備，可以給出S*中的積分。

定義3設函數Z是R到S*中一個給定的映射，并且對任意F∈S，t∈R，有《Z（t），G》∈L1（R），那么存在S*中的唯一元素，滿足

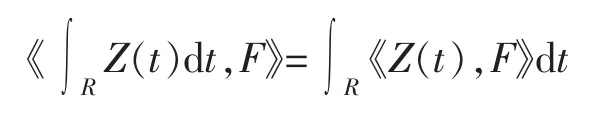
如果上述等式成立，則稱Z是S*可積的。

定理2分數次白噪聲WH（t）是S*可積的，并且

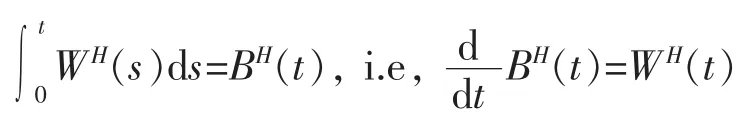
下面可以給出Wick積的定義。

定義4（S*中的Wick積）令以及，則Wick積的定義為

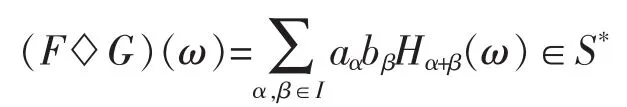
定義5中的Wick積）設，則這兩個函數的Wick積定義成

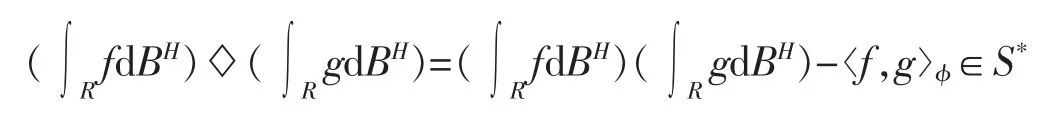
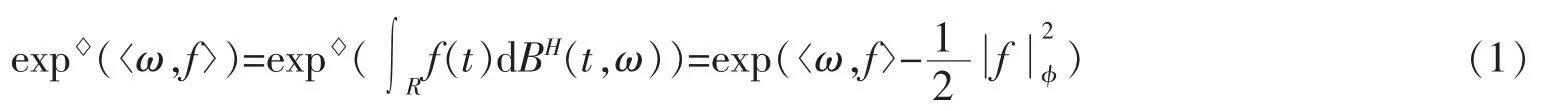
定義6（分數Wick-It?型積分）令函數Y：R→S*，如果Y（t）◇WH（t）在S*中可積，那么稱

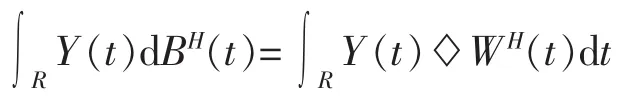
為函數Y的分數Wick-It?型積分。

為了介紹分數布朗環境下的It?法則，下面引進方向導數的概念。

定義7（方向導數）給定一個函數F：S（R）→R，并且γ∈S（R），如果

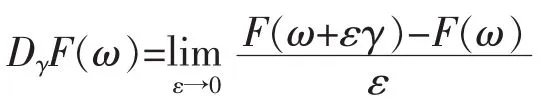
在S*中存在，那么稱F在γ方向上有一個方向導數，記為DγF。

定理3如果f（t）是一個適應過程，

定理4（分數It?法則）如果f∈C2（R×R），并且

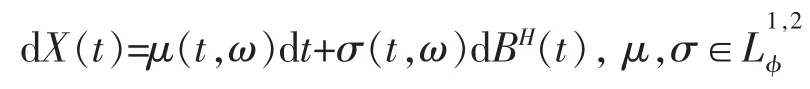
那么

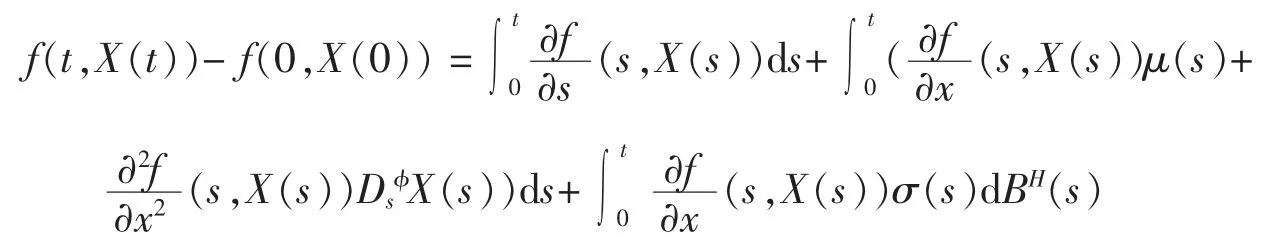
將分數布朗運動的It?法則與標準布朗運動的It?法則比較可知，原先It?法則中項的系數被Malliavin導數代替了。

定理5（分數Girsanov定理）設γ是一個連續函數，并且suppγ?[0，T]，K是一個函數，suppK?[0，T]并且滿足

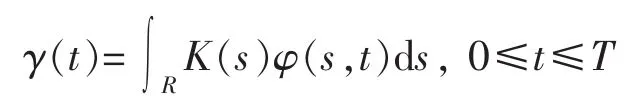
定義一個由{BH（t）：0≤t≤T}生成的新概率測度?滿足

在新的概率測度P?下

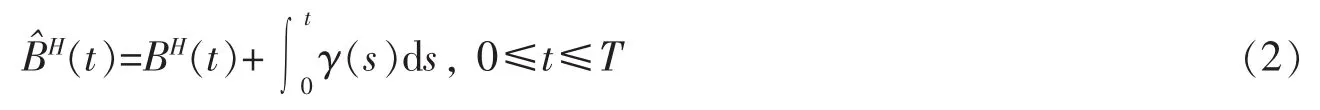
是一個分數布朗運動。

1.3 擬條件期望和擬鞅

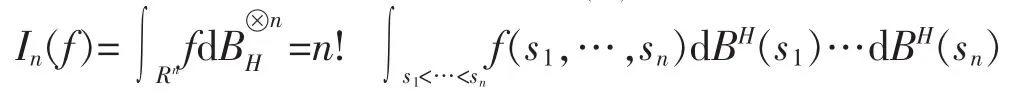
定理6（分數Wiener-It?混沌分解定理）令X∈L2（μ），則存在，使得

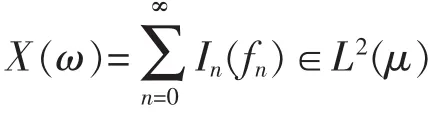
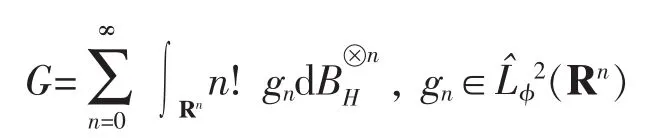
屬于空間G-q，q∈N，如果有。

定義8（擬條件期望）令，定義G中關于的擬條件期望為

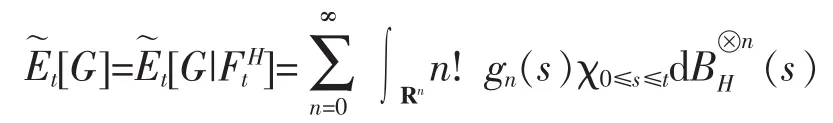
定義9（擬鞅）若隨機過程M（t，ω）是關于FtH適應的，如果M（t）∈G，?t，滿足，?t≥s，則稱M（t，ω）為擬鞅。

關于擬鞅，有下列三個重要性質：

（1）BH（t）是擬鞅；

有了擬條件期望，下面給出一對期權定價很重要的定理：

定理7函數f滿足E（f（BH（t）））＜∞，則對于任意t≤T，有

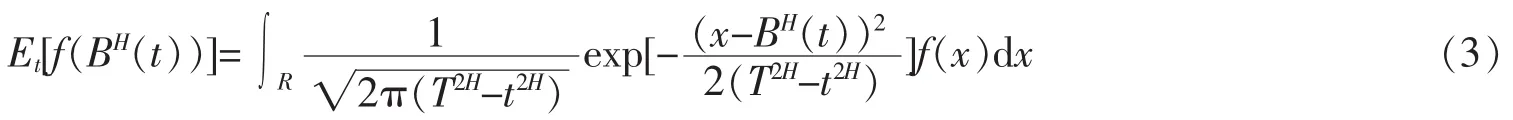
具體證明過程詳見文獻[7]。

最后，給出分數Clark-Ocone定理：

定理8（分數Clark-Ocone定理）

（1）令F∈G*且為FTH可測，則并且；

（2）令F∈L2（P）且為FTH可測，則并且。

1.4 泊松過程

泊松過程是一類時間連續、狀態離散的隨機過程。在實際問題的應用中，一般用泊松過程來研究一定時間間隔內某隨機事件出現的統計規律[8]。

定義10（泊松過程）計數過程{N（t），t≥0}稱為強度為λ泊松過程，如果滿足：

（1）在不相重疊的區間上的增量具有獨立性；

（2）$N（0）=0；

（3）對于充分小的Δt，P{N（t，t+Δt）=1}=λΔt+o（Δt），即在充分小的時間間隔中事件出現一次的概率與時間間隔的長度成正比；

由上述定義的泊松過程，給出其分布：

定理9（強度為λ泊松過程的分布）強度為λ泊松過程N（t）具有分布

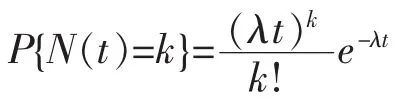
定理10（強度為λ泊松過程的鞅性）設N（t）是強度為λ＞0的泊松過程。定義補償泊松過程為M（t）= N（t）-λ是鞅。

金融市場中一般用泊松過程N（t）來表示突發事件發生的次數，用一個隨機變量Y（i）來表示每次事件發生時帶來的影響。若考慮總的影響，則有，這一新的隨機過程就是接下來要介紹的復合泊松過程。

定義11（復合泊松過程）{Y（i），i=1，2，…}是一列獨立同分布的隨機變量序列，N（t）是強度為λ＞0的泊松過程，Y（1），Y（2），…兩兩獨立，并且也獨立于N（t）。令，則稱{Y（i），i=1，2，…}為復合泊松過程。

下面給出復合泊松過程的兩個性質：

（1）Q（t）是一個獨立增量過程；

（2）Q（t）的特征函數為gQ（t）（u）=exp{λt[gY（u）-1]}，其中gY（u）是隨機變量Y的特征函數。

下面給出帶跳擴散過程的It?法則：

定理11（帶跳擴散過程的It?公式）若一過程滿足下列表達式[9]

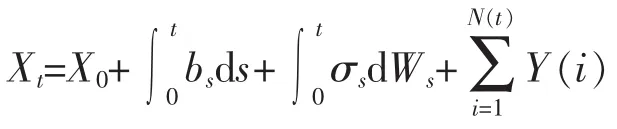
其中bs和σs是確定性過程，且，則有

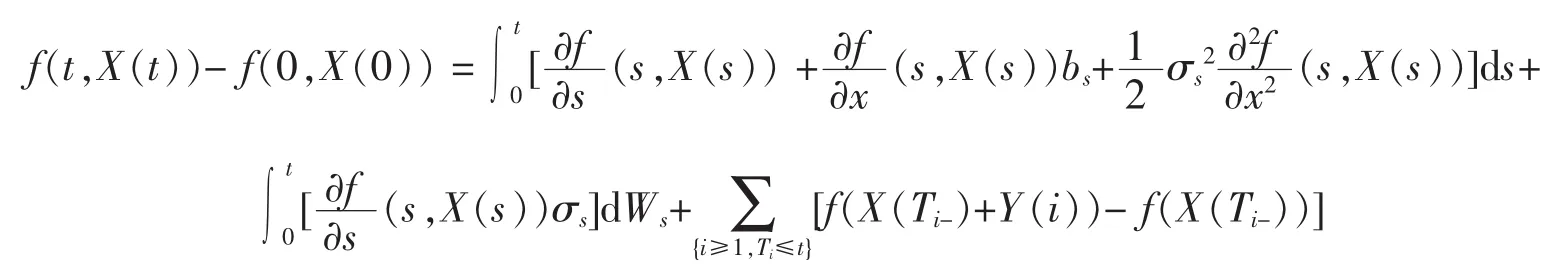
2 期權定價公式的推導

上節討論了分數布朗運動及其積分的有關內容。該節主要討論其在金融方面上的應用。與經典的Black-Scholes模型所作的基本假設相似，做如下假設：

（1）無風險利率r已知，且為常數。

（2）金融市場上只存在兩種資產，一種是股票（標的資產），其價格運動過程滿足

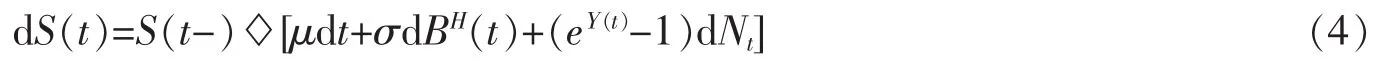
這里積分表示Wick型積分，μ表示預期收益率，σ表示股票價格的波動率。

該模型還考慮了市場的突發風險，即用上式的第三項表示，其中Nt表示影響股票價格突發事件發生的次數，假設其服從強度為λ的泊松分布；eY（t）-1表示股票價格跳躍的幅度，假設Y（t）服從正態分布N（m，δ2）。還假設以上三種分布均獨立。

另一種是無風險利率，即銀行存款，它的價格過程為dA（t）=rA（t）其中r是無風險利率。

（3）在衍生證券的有效期內，標的股票沒有紅利支付。

（4）期權為歐式期權。

（5）對于股票市場、期權市場和資金借貸市場來說，不存在交易費用和稅收等。

（6）投資者可以自由借入和貸出資金，借入利率和貸出利率相等，均為無風險利率。而且所有資產都是高度可分的，即投資者可以購買任意數量的標的股票和債券。

（7）對賣空沒有任何限制（如不設保證金），允許使用全部所得賣空衍生證券。

有了上述的假設，下面來求得期權的價格。

下面先考慮文中股價模型（4）[10]

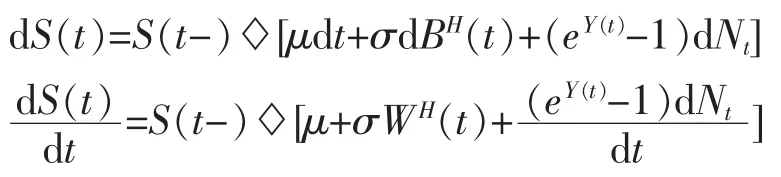
由Wick積分的定義5或（1）式得

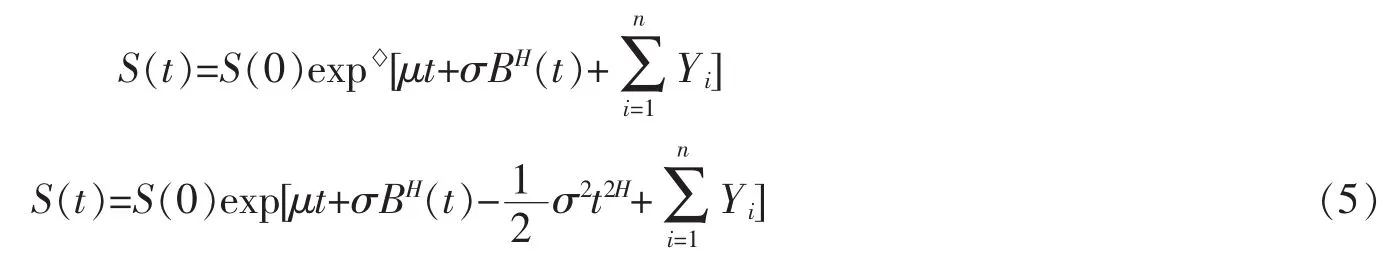
由于帶跳的股票模型是不完備的，下面利用測度變換的辦法給出其風險中性定價公式[1，11]。

定理12在股票服從上述公式時，期權的價格為Z（0）=e-rtE[Z（t）]，其中r是無風險利率。

證明設存在一可復制策略（u（t），v（t））；A（t）代表債券的價格過程；S（t）代表股票的價格過程。則

設該過程是自融資過程，則有

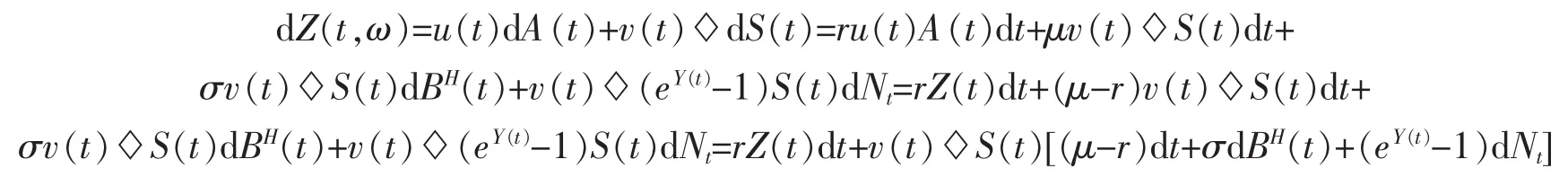
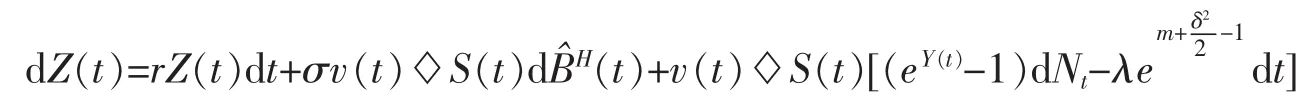
兩邊乘以e-rt并積分得

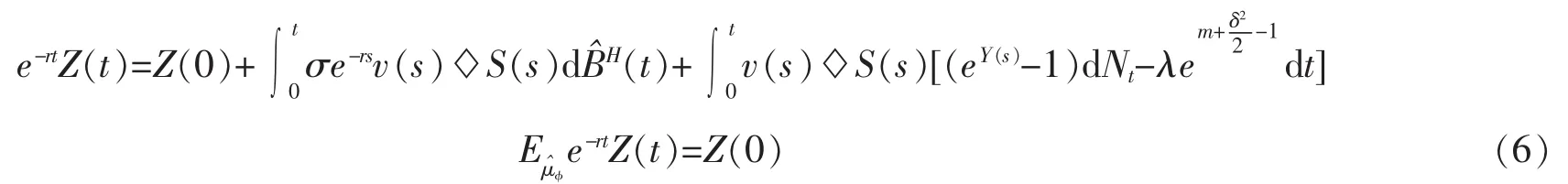
已有標的股價模型（4）及其具體表達式（5），接下來來考慮由此衍生出來的一類新型期權-冪期權的定價。冪式期權是一種新型期權。它與一般期權的不同之處在于執行時標的資產的價值被提高到某次冪。根據到期日的執行條件不同，冪期權可分為兩類：

定理13第一類歐式冪式期權：C（T）=（Sn（T）-K）+的價格為

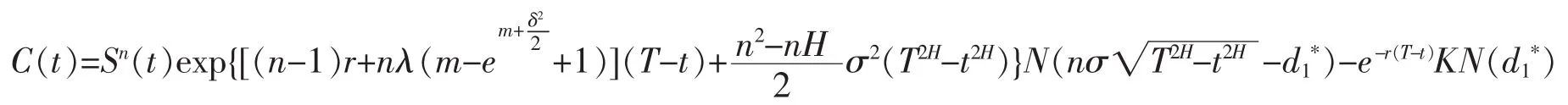
證明將股價模型（5）代入（6）得

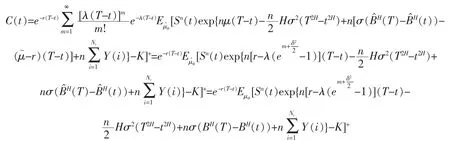
由定理7及公式（3）得

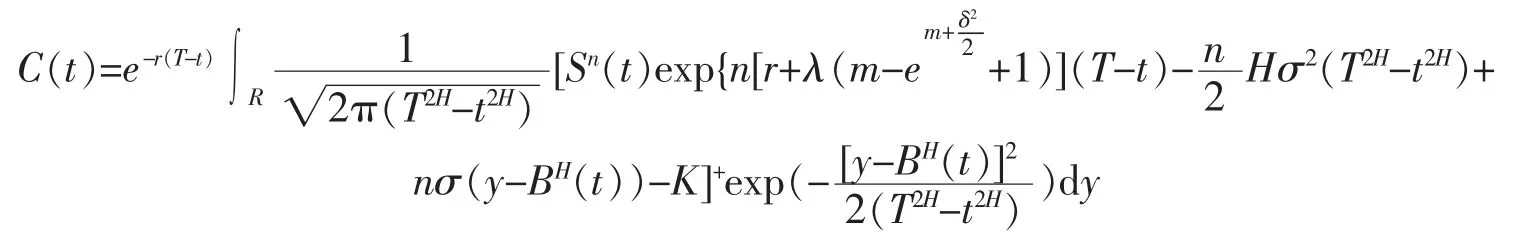
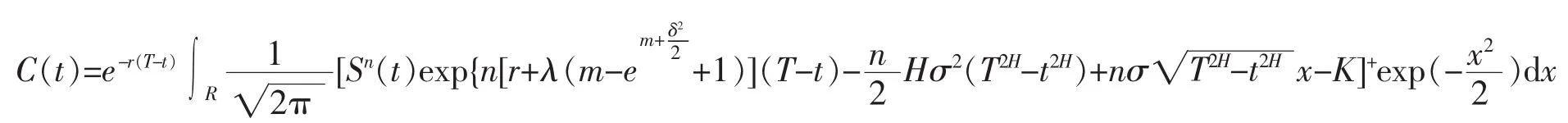
考慮定義域，對于

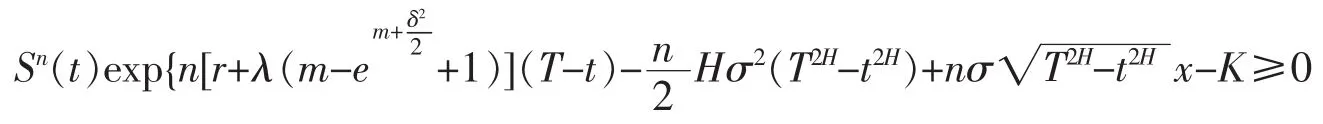
時，有

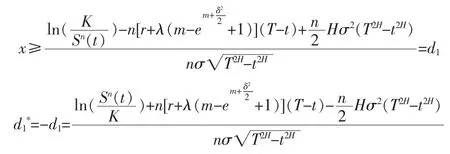
此時期權定價公式可以繼續簡化得

得結論。

定理14第二類歐式冪式期權：的價格為

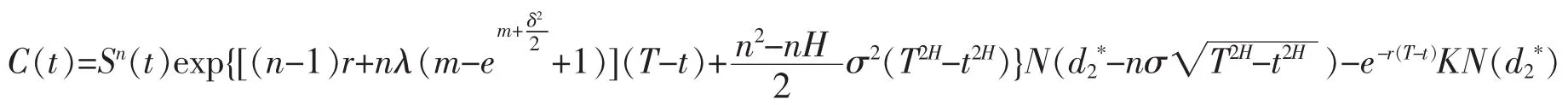
證明先考慮定義域，當

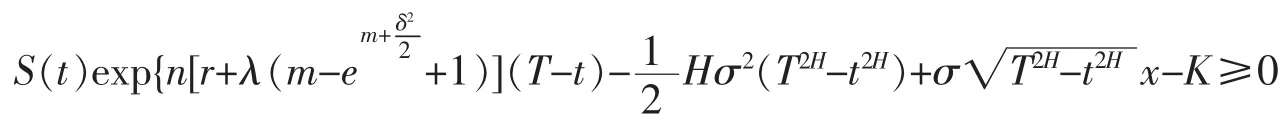
時，有

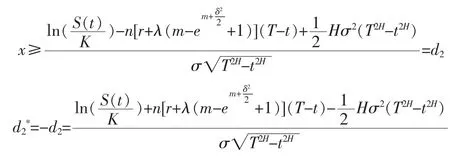
其他解答過程與定理2類似，此處便不累述了。

3 結語

筆者主要研究了分數布朗運動環境下帶泊松跳的期權的定價問題。由于價格模型帶跳時是有套利的，文中便利用測度變換的辦法，給出其定價的公式并解出了具體的冪式期權定價表達式。在今后的研究中還可以進一步考慮波動率和期望收益率是隨機時的冪式期權的定價，還可以用其他函數來刻畫突發事件的影響。

[1]Hu Y，?ksendal B.Fractional white noise caculus and applications to finance[J].J Inf Dim Anal Quantum Probab Rel Top，2003，6：1-32.

[2]劉韶躍，楊向群.標的資產價格服從幾何分數布朗運動的歐式雙向期權定價[J].湘潭大學學報：自然科學版，2004，26（2）：1-4.

[3]趙佃立.分數布朗運動環境下歐式冪期權的定價[J].經濟數學，2007，24（1）：22-26.

[4]Mishura Y.Stochastic Calculus for Fractional Brownian Motion and Related Processes[M].Berlin and Heidelberg：Springer-Verlag，2008.

[5]Dunean T E，Hu Y，Pasik-Duncan B.Stochastic caleulus for fractional Brownian motion[J].I Theory SIAM J Control Optim，2000，38：582-612.

[6]Aase K，?ksendal B，Privault N，et al.White noise generalizations of the Clark-Haussmann-Ocone theorem with application to mathematical finance[J].Finance and Stochastic，2000，4：465-496.

[7]Neeula C.Option pricing in a fractional brownian motion environment[J].Academy of Economic Studies，2002，1：1-50.

[8]黃文禮.基于分數布朗運動模型的金融衍生品定價[D].杭州：浙江大學，2011.

[9]Cont R，Tankov P.Financial Modelling with Jump Processes[M].Boca Raton：Chapman and Hall/CRC，2004.

[10]Sattayatham P，Intarasit A，Chaiyasena A P.A fracitonal Black-Scholes model with jump[J].Vietnam J Math，2007，2：1-15.

[11]Merton R C.Option pricing when underlying stock returns are discontinuous[J].J Financial Economics,1976，3：125-144.

European power option pricing under the environment of Fractional Brownian Motion with Poisson jump

YI Xiaolan，ZHANG Qinghua，YAN Litan
（College of Science，Donghua University，Shanghai 201620，China）

In this paper we assume that the underlying stock price is subject to the Poisson jump process under the Fractional Brownian Motion environment.By the measure transformation method，we have selected different probability measures and successfully given the power option pricing.

Fractional Brownian Motion（FBM）；Poisson jump process；European power option

O211.6MR（2000）Subject Classification：60G15；60H05

A

1672-0687（2015）02-0010-09

責任編輯：謝金春

2013-09-28

國家自然科學基金資助項目（11171062）；上海教委重點資助項目（12ZZ063）

易小蘭（1988-），女，湖北宜昌人，碩士研究生，研究方向：隨機分析及金融應用。

*通信聯系人：閆理坦（1961-），男，教授，博士，博士生導師，E-mail：litanyan@dhu.edu.cn。