形如Δ2u=f1(x)f2(y)的泊松方程齊次化判定方法

馬春蘭，臧濤成，葛麗娟

（蘇州科技學院數理學院，江蘇蘇州215009）

形如Δ2u=f1(x)f2(y)的泊松方程齊次化判定方法

馬春蘭，臧濤成，葛麗娟

（蘇州科技學院數理學院，江蘇蘇州215009）

討論了形如Δ2u=f1(x)f2(y)的泊松方程齊次化問題，給出了判定該類型泊松方程是否能夠進行齊次化的判別式以及求解其特解的方程。

泊松方程；非齊次項；定解問題；特解

泊松方程Δ2u=f在靜電場電勢、穩定溫度分布等許多數學物理及工程技術領域中都會涉及。理論上該方程可采用格林函數積分法進行求解[1-2]，但該法積分運算比較復雜，一般難以得到直接的解析解。另一種解法為齊次化方法[1-8]，即將原關于u的泊松方程通過某種方式（如找特解）轉化為可采用分離變量法求解的拉普拉斯方程，采用的方法基本是羅列方程非齊次項f呈現何種特殊形態時方程可齊次化。那么，對泊松方程是否存在一個統一的判定方法呢？筆者針對這一問題，對形如Δ2u=f1(x)f2(y)的泊松方程進行了分析，得到了判定該類型泊松方程是否能夠進行齊次化的判別方法及求解其特解的方程。

1 Δ2u=f1(x)f2(y)齊次化判定條件及特解滿足的方程

不失一般性，考慮如下直角坐標下的泊松方程第一邊值問題（定解條件全為非齊次時可用疊加原理化為包括下述（1）在內的兩個定解問題，另一個則可用熟悉的分離變量法求解）

如何才能夠判定定解問題（1）中方程能夠齊次化（當然方程齊次化后的定解問題也要有一組邊界條件保持齊次）呢？或者說，非齊次項必須滿足什么條件才能保證（1）可以齊次化？

為此，令

其中g(y)≠0是待求函數。通過（2）式，將原關于u(x,y)的泊松方程定解問題轉化為關于v(x,y)的拉普拉斯方程定解問題。v(x,y)顯然應滿足

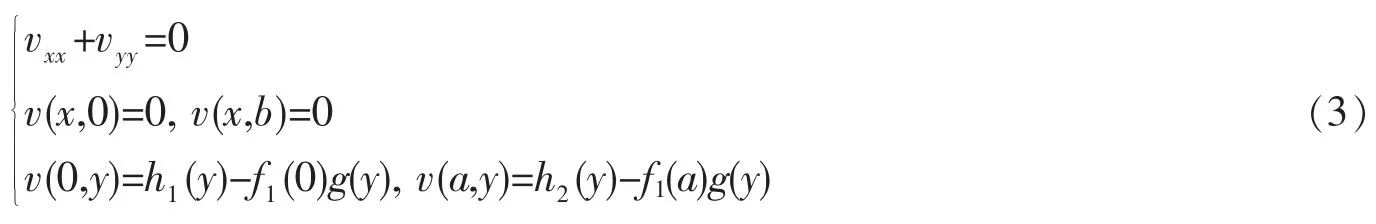
為尋求f1(x)滿足何種條件才能找到待求函數g(y)，將（2）代入（1）有

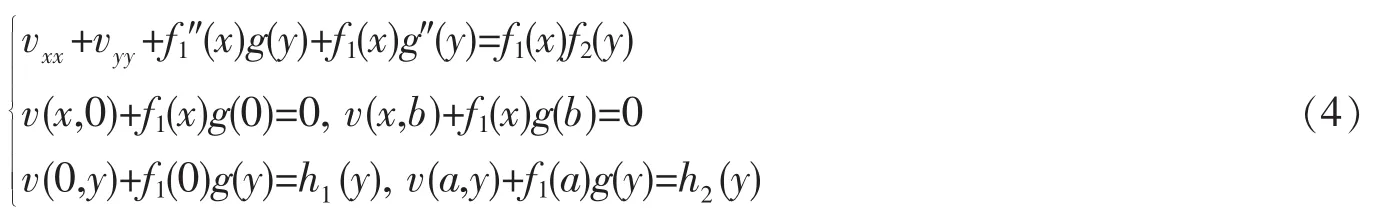
考慮到（3），顯然應有

由（5）之第一式可得

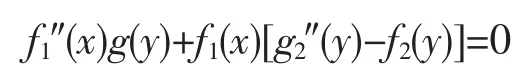
因g(y)≠0，所以

左邊為x的函數與y無關，右邊為y的函數與x無關，（6）式成立的條件是等式兩邊同時等于一常數k，即

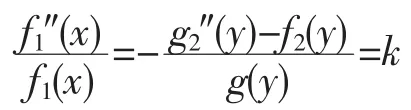
由此可知，當f1(x)滿足

時，也即f1(x)為線性函數（k=0）、e的指數函數（k＞0）（或雙曲函數）或正余弦三角函數（k＜0）時，待求函數g(y)存在，定解問題（1）能夠進行齊次化。

此時，待求函數g(y)滿足的方程為

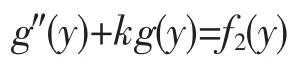
由上式和（5）之第二式可得完全確定g(y)的如下表達式

至此，對定解問題（1），只要f1(x)滿足（7）式，就可通過（8）式求得g(y)，從而得到齊次化函數f1(x)g(y)，進而通過（3）式和（2）式最終求得（1）式的解。

2 推論

（1）對于其他邊界條件情形（如第二類或混合邊界條件），根據（4）知（8）式仍然適用；

（2）以上結論可適用于滿足（7）式的各種函數的若干加減組合（見例題2）；

（3）對于形如

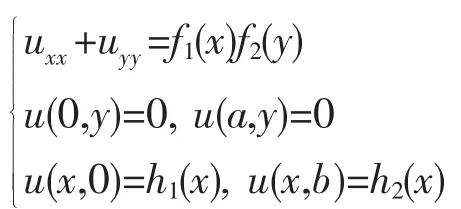
的定解問題，只要f2(y)滿足（7），那么齊次化函數f2(y)g(x)中的g(x)完全類似于（8）

3 實例

例1求定解問題[2]。

解f1(x)=x，f2(y)=-2A，滿足判定式（7）f1″(x)=kf1(x)且k=0，定解問題的方程和邊界條件可同時齊次化。由（8）得

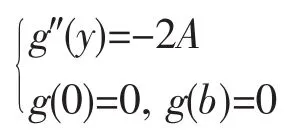
解得

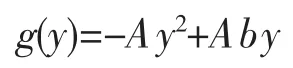
代入（2）式中有

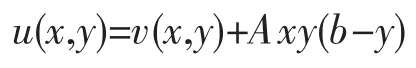
再由（3）式得

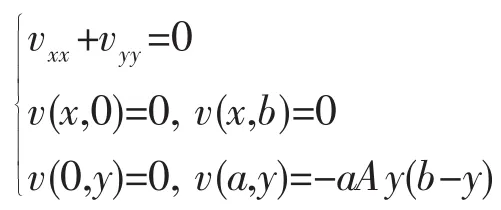
采用分離變量法求得解為

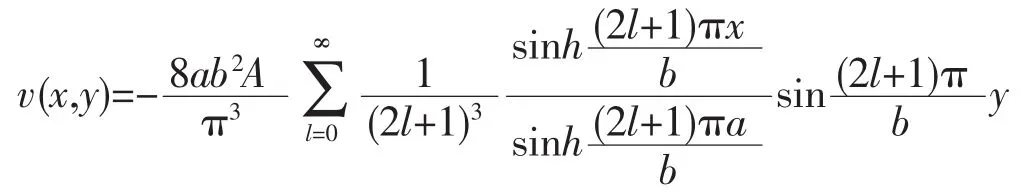
最后

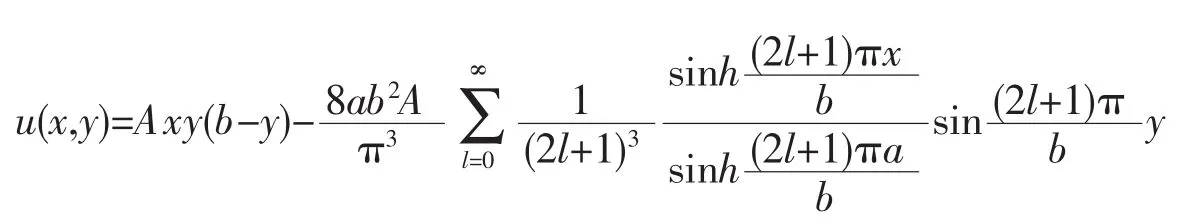
此題在文獻[2]中是用猜的方法得到能同時使得變換后v(x,y)的方程及y方向邊界條件同時為齊次的特解Axy(b-y)，這在非齊次項相對簡單（如例1）時還可能做到，但對復雜一些的情況（如例2）就不那么容易用猜的辦法了。

例2對定解問題

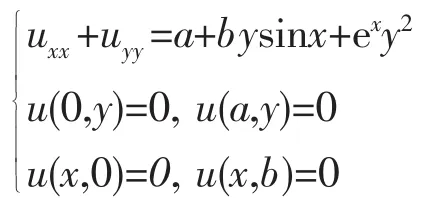
設u=v+w，試求特解w，使得變換后關于v的方程和一組邊界條件為齊次。

解將定解問題化為（1）的形式。為此令，并設及ui的特解為wi，這樣

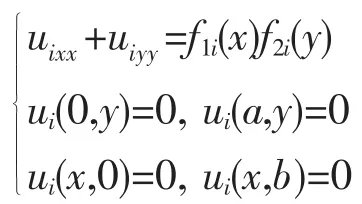
i=1時：可令f11(x)=a，f21(y)=1，故有k=0，由（8）

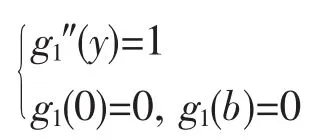
得

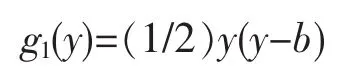
特解為

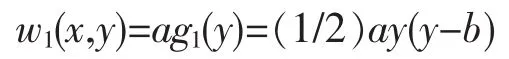
i=2時：f12(x)=sinx，f22(y)=y，因y″=0·y和(sinx)″=-sinx，故可取k=0或k=-1，考慮到i=1時在y方向邊界條件為齊次，所以取k=-1。這樣，由（8）

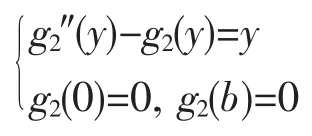
得

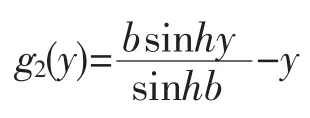
特解為

i=3時：f13(x)=ex，f23(y)=y2，因（ex）″=ex，故k=1，由（8）

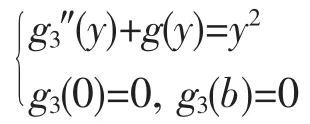
得

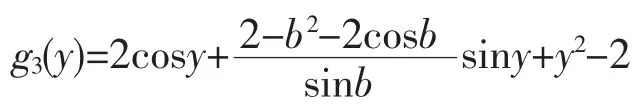
特解為

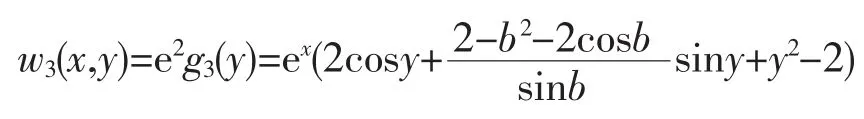
這樣

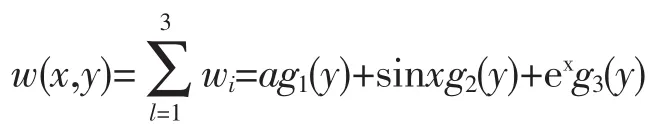
因為

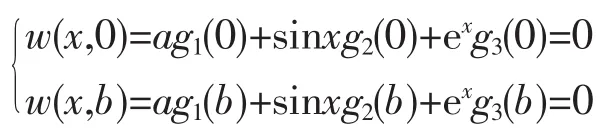
所以w(x,y)就是所要求的原問題的特解。

[1]梁昆淼.數學物理方法[M].3版.北京：高等教育出版社，1998：148-150，220.

[2]周治寧.數學物理方法習題指導[M].北京：北京大學出版社，2004：212-213.

[3]臧濤成.具有特殊非齊次項泊松方程的特解法[J].大學數學，2011，27（2）：138-141.

[4]臧濤成.具有特殊非齊次項波動方程的處理方法[J].大學物理，2009，28（3）：10-12.

[5]石文善.線性偏微分方程非齊次定解問題的待定函數法[J].大學物理，1992，28（3）：10-12.

[6]楊燕.關于泊松方程的解[J].文山高等師范專科學校學報，2002，14（1）：65-68.

[7]李其深.一種求泊松方程特解的方法[J].工科數學，1994（2）：110-114.

[8]夏志.泊松（Poisson）方程特解的待定函數解法[J].遼寧工學院學報，2006，26（1）：66-69.

The homogeneous method of Poisson equation such as Δ2u=f1（x）f2（y）

MA Chunlan，ZANG Taocheng，GE Lijuan
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

The transformation of nonhomogeneous Poisson equations such as Δ2u=f1(x)f2(y)into homogeneous equations is discussed.We proposed a criterion for this kind of Poisson equations being able to be homogenized. And the equation for the special solution was given.

Poisson equation；nonhomogeneity；definite problem；particular solution

O411.1

A

1672－0687（2015）02－0033－04

責任編輯：李文杰

2014－12－17

國家自然科學基金資助項目（11304218）；校重點專業建設資助項目（2013zyxz-08）

馬春蘭（1973-），女，江蘇鹽城人，副教授，博士，研究方向：凝聚態物理等。