加權有窮自動機的代數性質*
張麗霞
(安慶師范學院數學與計算科學學院,安徽 安慶 246013)
加權有窮自動機的代數性質*
張麗霞
(安慶師范學院數學與計算科學學院,安徽 安慶 246013)
在加權有窮自動機理論基礎上,利用強同態的概念,證明兩個加權有窮自動機在計算能力上是等價的,并在加權有窮自動機的狀態集上建立一種等價關系,得到加權有窮自動機的商自動機,證明加權有窮自動機與其商自動機在計算能力上也是等價的。并通過引入加權有窮自動機的可交換性、分離性、(強)連通性及層的概念,討論在(強)同態的條件下,兩個加權有限狀態機之間的可交換性、分離性、(強)連通性及層的關系。
形式冪級數;加權有窮自動機;同態;強連通
1 引言
在計算機科學中,自動機作為計算過程的動態數學模型,用來研究計算機的體系結構、邏輯操作、程序設計乃至計算復雜性理論[1~5]。1961年,Schützenberger M P[6]首先提出了加權自動機的概念,并提出了半環上的形式冪級數的概念,證明了Kleene-Schützenberger 定理,即加權有窮自動機所識別的形式冪級數和有理冪級數是一致的。隨后,又有很多學者在這一領域作出了進一步有意義的工作[7~12]。目前,加權自動機在模式識別、模型檢測、數字圖像壓縮算法等領域取得了廣泛的應用[13~15]。由于 Successor 和Source 算子是自動機理論中的重要工具之一,Kuroki N、Tiwari S P,Srivastava A K等[16~21]利用 Successor 和 Source算子研究了模糊有窮自動機(強)連通性、分離性、交換等性質,并給出了模糊自動機一些結構刻畫。本文將在半環的結構上,研究加權有窮自動機的同態和強同態及其性質,并在加權有窮自動機的狀態集上建立一種等價關系,從而得到加權有窮自動機的商自動機。進一步,利用(強)同態的概念,討論了兩個加權有限狀態機之間的可交換性、分離性、(強)連通性及層的關系。
2 基本概念與符號
首先,我們引入一些必要的概念與記號,詳細請參考文獻[11,12,17,20]。
集合S是帶有兩個二元運算⊕、?和兩個特殊元素0、1的集合,并且滿足:
(1)(S,⊕,0)是交換幺半群;
(2)(S,?,1)是幺半群;
(3) 對任意a,b,c∈S,有a?(b⊕c)=a?b⊕a?c,(b⊕c)?a=b?a⊕c?a;
(4) 對任意a∈S,有0?a=a?0=0。
稱(S,⊕,?,0,1)為半環。為了方便討論,本文簡記S。如果對任意a,b∈S,都有ab=ba,則稱半環S為交換半環。半環理論作為具有廣泛應用背景的代數系統在計算機理論科學中具有特殊性及重要性。特別在經典的形式語言理論中,最重要的半環是Boolean半環S={0,1}。
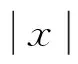
設S是一個半環,稱Σ*到S的映射A為形式冪級數。對任意x∈Σ*,A在x處的值記為(A,x),并記A為:
稱A為變量在Σ中的形式冪級數,其中(A,x)為此形式冪級數的系數。所有形式冪級數組成的集合記為S?Σ*。
設A,B∈S?Σ*,若對任意x∈Σ*,有A(x)=B(x),則稱A等于B,記作A=B。
定義1[11]設S是半環,加權有窮自動機(簡記為WFA)(WeightedFiniteAutomata)是五元組W=(Q,Σ,δ,I,F),其中,Q為有限狀態集合,Σ為有限輸入字符集,I:Q→S與F:Q→S分別代表權值初始狀態與權值接受狀態,而δ:Q×Σ×Q→S為權值轉移函數。
更進一步,若對q∈Q,x∈∑,存在唯一的p∈Q使得δ(q,x,p)=1,而對其余的r∈Q,都有δ(q,x,r)=0,并且存在唯一的q′∈Q使得I(q′)=1,則得到通常的確定型加權有窮自動機的概念。
轉移函數δ可以擴張到Q×∑*×Q上,即δ*:Q×∑*×Q→S滿足如下條件:
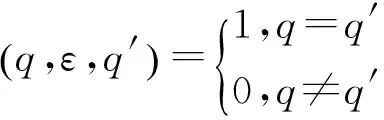
(2) 對輸入序列x=x1x2…xk∈∑*,k≥1,則:
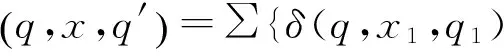
根據上述定義,易驗證下列等式成立:

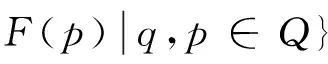

另外,對任意A∈S?Σ*,若存在一個WFAW使A恰為W接受的形式冪級數,則稱A為Σ上的正則冪級數。
為了對不同的加權有窮自動機進行比較,下面引入加權有窮自動機之間同態和強同態的概念。
定義3[11]設S是半環,W=(Q,Σ,δ,I,F)和W1=(Q1,Σ,δ1,I1,F1)是兩個WFA。設映射φ:Q→Q1,對任意q,q′∈Q,x∈Σ,若滿足下列條件:
I(q)≤I1(φ(q)),F(q)≤F1(φ(q)),δ(q,x,q′)≤δ1(φ(q),x,φ(q′))
則稱φ為同態映射。
進一步,若φ滿足:
F1(φ(q))=F(q)。
則稱φ為強同態。若φ是強同態且同時是雙射,則稱φ為同構。
Successor算子是自動機理論中的重要工具之一。在文獻[22]中,Zamir B首先提出了Successor算子的概念,并利用Successor算子研究了有窮自動機一些特有的性質。近年來,Tiwar S P等[19~21]在模糊集合的理論基礎上,利用Successor算子給出了模糊有窮自動機一些結構刻畫。本文將利用Successor算子來定義加權有窮自動機的交換性、強連通性、分離性等概念,利用這些概念來討論加權有窮自動機的一些特性。
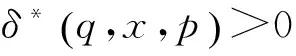
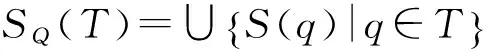
定義5設S是半環,W=(Q,Σ,δ,I,F)是一個WFA,則:
(1) 對任意p,q∈Q,若q∈S(p)當且僅當p∈S(q),則稱W滿足交換性。
(2) 對任意p,q∈Q,都有p∈S(q),則稱W是強連通的。
(3)T?Q,δ是T×Σ×T的一個加權子集。若滿足以下兩個條件:
①δ|T×Σ×T=η;
②SQ(T)?T。
則稱N=(T,Σ,η,I|T,F|T)是W的子加權有窮自動機。若T≠Q且T≠?,則稱N是W的真子加權有窮自動機。
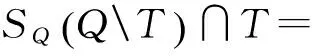
定義7設S是半環,W=(Q,Σ,δ,I,F)是一個WFA。如果W是沒有可分離的真子加權有窮自動機,則稱W是連通的。
3 主要結果
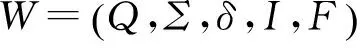

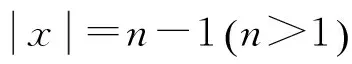
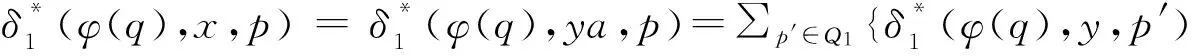
∑p′∈Q1{∑s∈Q{δ*(q,y,s)|φ(s) =p′} ?∑p∈Q1{δ*(s,u,r)|φ(r)=p}}=
∑p′∈Q1{∑r,s∈Q{δ*(q,y,s)|φ(s) =p′} ?{δ*(s,u,r)|φ(r)=p}}=
∑r∈Q{δ*(q,yu,r)|φ(r)=p}
充分性。因為φ是單射,故對任意q,r∈Q,且x∈Σ*,有:
因此,φ是強同態。
□
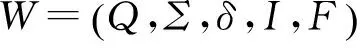
證明對任意x∈Σ*,有:



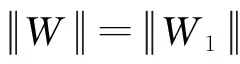
□
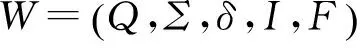
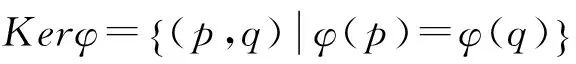



證明對任意x∈Σ*,有:

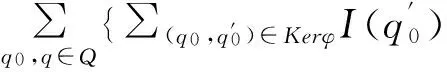
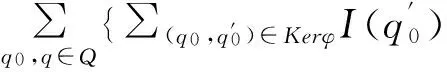

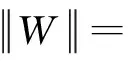
□
定理3說明了加權有窮自動機與其商自動機在計算能力上是等價的,從而實現了加權有窮自動機的狀態極小化。
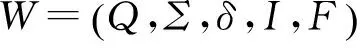
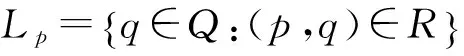
引理1[19]設S是半環,W=(Q,Σ,δ,I,F)是一個WFA,則W是強連通的充分條件是W沒有真子加權有窮自動機。
定理5設S是半環,W=(Q,Σ,δ,I,F)是一個WFA,則:
(1) 若W是強連通的當且僅當W是連通的且滿足交換性;
(2) 若W是強連通的,則Q自身為W的一個層。
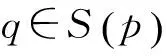
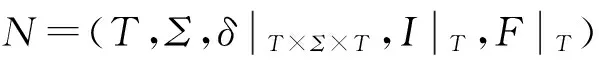
(2) 顯然,若W=(Q,Σ,δ,I,F)是強連通的當且僅當S(q)=Q,q∈Q,根據可分離的定義,Q為W的一個層。
□
定理6設S是半環,W=(Q,Σ,δ,I,F)是一個WFA,則W必有一個強連通的子加權有窮自動機。
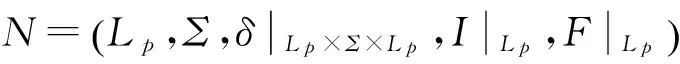
□
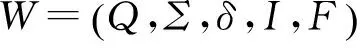

(2) 若p∈Q,Lp為W的一個層,則φ(Lp1)為W1的一個層。
證明(1) 根據加權有窮自動機同態的定義可得。
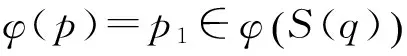
□

根據引理2,我們有如下結論。
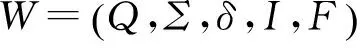
4 結束語
本文在半環的結構上,利用強同態的概念,證明了兩個加權有窮自動機在計算能力上是等價的,并在加權有窮自動機的狀態集上建立了一種等價關系,得到了加權有窮自動機的商自動機,證明了加權有窮自動機與其商自動機在計算能力上也是等價的,從而實現了加權有窮自動機的狀態極小化。此外,我們給出了加權有窮自動機的可交換性、分離性、(強)連通性及層的概念,討論了在(強)同態的條件下,兩個加權有限狀態機之間的可交換性、分離性、(強)連通性及層的關系。這些研究結果進一步豐富了加權自動機的理論。
[1] Shannon C E, MeCary J. Automata studies[M]. Prineeton:Prineeton University Press, 1956.
[2] Hopcroft J E, Ullman J D. Introduction to automata theory, languages and computation[M]. New York:Addison-Wesley, 1979.
[3] Zadeh L A. Outline of a new approach to the analysis of complex systems and decision processes[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1973(1):28-44.
[4] Mordeson J N, Malik D S. Fuzzy and languages:Theory and applications[M]. Boca Paton:Chapman &Hall/CRC, 2002.
[5] Malik D S, Mordeson J N, Sen M K. On subsystems of a fuzzy finite state machines[J]. Fuzzy Sets and Systems,1994,68(2):83-92.
[6] Schützenberger M P. On the definition of a family of automata[J]. Information and Control,1961(4):245-270.
[7] Salomaa A, Soittola M. Automata theoretic aspects formal power series[M]. Berlin:Springer, 1978.
[8] Droste M,Kuich W,Vogler H.A Kleene theorem for weighted tree automata[J]. Theory of Computing Systems, 2005,38(1):1-38.
[9] Droste M, Gastin P. Weighted automata and weighted logics[J]. Theoretical Computer Science,2007,380(1-2):69-86.
[10] Berstel J, Reutenauer C. Noncommutative rational series with applications, encyclopedia of mathematics and its applications[M]. Cambridge:Cambridge University Press, 2010.
[11] Li Y M,Wang Q.The universal fuzzy automation[J].Fuzzy Sets and Systems,2014,249:27-48.
[12] Li Y M. Analysis of fuzzy systems[M].Beijing:Science Press,2005.(in Chinese)
[13] Ong G H, Kai Y. A binary partitioning approach to image compression using weighted finite automata for large images[J]. Computers & Mathematics with Applications, 2006, 51(11):1705-1714.
[14] Albert J, Kari J. Digital image compression[M]∥Handbook of Weighted Automata[M]. Berlin:Springer -Verlag,2009(Chapter11).
[15] Bouyer P. Weighted timed automata:Model-checking and games[J]. Electronic Notes in Theoretical Computer Science, 2006, 158(5):3-17.
[16] Kuroki N, Mordeson J N. Successor and source functions[J]. J Fuzzy Math, 1997(5):173-182.
[17] Srivastava, A K, Tiwari S P. A topology for fuzzy automata [C]∥Proc of AFSS’02, 2002:485-490.
[18] Srivastava A K , Tiwari S P. On another decomposition of fuzzy automata [J]. Journal of Uncertain Systems, 2011,5(1):33-37.
[19] Tiwari S P, Singh A K, Sharan S. Fuzzy automata based on lattice-order monoid and associated topology[J]. Journal of Uncertain Systems, 2012,6(1):51-55.
[20] Tiwari S P, Sharan S. Fuzzy automata based on lattice-ordered monoid with algebraic and topological aspects[J]. International Journal of Fuzzy and Information Engineering, 2012, 4(2):155-164.
[21] Tiwari S P,Yadav V K,Anupam K S.On algebraic study of fuzzy automata [J]. International Journal of Machine Learning and Cybernetics,doi:10.1007/s13042-014-0233-5.
[22] Zamir B. Introduction to the theory of automata[M]. Virginia:Reston Publishing Company, 1983.
附中文參考文獻:
[12] 李永明. 模糊系統分析[M].北京:科學出版社,2005.
ZHANGLi-xia,born in 1984,MS,lecturer,her research interests include representation theory of algebras, and algebraic theory of automata.
Algebraicpropertiesofweightedfinitestateautomata
ZHANG Li-xia
(School of Mathematics and Computation,Anqing Normal University,Anqing 246013,China)
On the basis of the theory of weighted finite automata,we prove the computing equivalence between two weighted finite automatas under the strong homomorphism of weighted finite automatas, and obtain the quotient weighted automata by establishing the equivalence relation on the states of weighted finite automata.Based on the equivalence relation,the equivalence between weighted finite automata and its quotient automata is also proved.Specifically,the concepts such as commutability,separateness,(strong) connectedness properties and layers of weighted finite automata are introduced,and their relations in two different weighted finite automata are discussed under the homomorphism or strong homomorphism.
formal power series;weighted finite automata;homomorphism;strong connectedness
1007-130X(2014)11-2186-05
2014-07-10;
:2014-09-16
安慶師范學院青年科研基金項目(KJ201214);安徽省優秀青年人才基金項目(2011SQRL097)
TP301
:A
10.3969/j.issn.1007-130X.2014.11.022

張麗霞(1984),女,安徽安慶人,碩士,講師,研究方向為代數表示論和自動機代數理論。E-mail:zhanglix84@163.com
通信地址:246013 安徽省安慶市安慶師范學院數學與計算科學學院
Address:School of Mathematics and Computation,Anqing Normal University,Anqing 246013,Anhui,P.R.China

