基于PHPSO－IA 的城市環境噪聲測點優化

趙鳳強，李廣強，胡紅英，張汝波，張 艷

(1.大連海事大學 信息科學技術學院，遼寧 大連116026;2.大連民族學院 機電信息工程學院，遼寧 大連116605;3.馬薩諸塞大學洛厄爾分校 計算機科學系，馬薩諸塞州 洛厄爾01854)

城市區域噪聲的監測是城市環境監測體系的一個重要組成部分，環境噪聲及時而準確地測量及評價有助于環境管理部門的宏觀控制，制定合理的環境保護政策和措施。城市環境區域噪聲的測量一般采用布點測量的方式。國標GB/T 14623 －93 給出有等網格布點測量和定點監測兩種方法。等網格布點方法在樣本數足夠大的情況下，其總體平均值具有統計意義，代表一個城市區域環境噪聲平均值，而其單個監測點和監測值，由于隨機性的原因，是無意義的。工程上一般在等網格布點測量的基礎上，再進一步進行布點優化。但是等網格布點測量一個待改進之處在于，它無法深入考慮由于城市建筑布局、人口分布等影響因素的不同而帶來的噪聲聲場分布不均勻現象。城市環境噪聲測量布點優化通常采用基于數理統計的抽樣和灰色理論關聯度分析等方法，在客觀性、可操作性等方面存在一定的局限性。測量布點問題歸根結底是一個優化問題。該問題屬于NPC 問題，較好地求解這類問題具有相當的難度。近年來遺傳算法在各類復雜系統優化問題中已有應用［1－4］，實踐證明其確實有效。但是，遺傳算法雖具有全局尋優的能力，然而它也存在早熟和收斂慢等缺陷［5－8］，需要進一步的改進，才能更好地應用于各種實際問題之中。本文以大連市噪聲測量布點優化問題為研究對象，基于變網格布點思想，提出了PHPSO－IA，求解了該問題。

1 城市環境區域噪聲測點優化問題

本文參考有限元分析時劃分網格的策略，提出了變網格測量布點的思想，并在其基礎上進一步研究高效的計算智能類布點優化算法。

1.1 變網格布點測量

根據城市建筑物、道路及人口分布等噪聲影響因素特點，在噪聲源復雜，聲場分布不均勻的地區加大測點劃分網格的密度，這樣便將待測區域劃分成為面積不完全相同的一系列網格，在實際的劃分中可為直線，也可為曲線，故而網格可以是不規則的。

設測點i 測得的噪聲聲級為Li，∑si=S，S為選取的n 個測點所在網格的總面積。面積權系數ai=si/S (i=1，2，…，n )，各網格面積不一定相等，故其面積權系數也不一定相同，但仍滿足歸一化條件。則有

本文提出的變網格測量布點，試圖使得網格疏密與建筑物、人口及聲場分布的特點相適應，從而有可能更客觀地對待測區域噪聲質量情況給予評價。

1.2 變網格噪聲測量布點優化問題的模型建立

以大連市中山區噪聲測量布點優化問題為例，對該區域噪聲采用變網格布點測量，2004 年大連市環境監測中心測量的112 個測點，其位置、面積、各測點對應的噪聲值和所屬功能區域參見文獻［9］。

在中山區區域噪聲變網格布點測量中共監測分屬五類功能區的112 個測點。其中0 類功能區是特殊住宅區(指大連棒槌島國賓館附近區域)，有3 個測點;Ⅰ類功能區是居住、文教機關區，有49 個測點;Ⅱ類功能區是居住、商業、工業混合區，有8 個測點;Ⅲ類功能區是工業區，有2 個測點;Ⅳ類功能區在道路交通干線兩側，有50 個測點。

設第i 類功能區的第j 個測點測得的等效連續A 聲級LeqA為Lij，其面積為sij，i=0，1，…，t;j=1，2，…，ki，此處t=4，ki為第i 類功能區總的測點數。采用類似背包問題的二進制編碼方案，串X 的長度等于ki=n，即等于待測區內的測點總數。類似地，xij=1 表示優化解選取第i 類功能區的第j 個測點，xij=0 則表示優化解舍棄第i 類功能區的第j 個測點。由此，可構造該問題的優化數學模型如下［9］:

上述模型的優化目標是優化后的測點越少越好;式(2)是保證優化前后整個待測區聲級的面積計權均值的絕對誤差不宜過大，式(3)和式(4)則是從數理統計的角度，保證優化前后測點噪聲聲級的均值、標準差等數字特征沒有明顯改變的約束，按相關資料的推薦及實際經驗，給出優化前后測點聲級的各種均值絕對誤差不超過1dB，以及優化前后測點聲級標準差的相對誤差不超過5%. 其中μw和分別為變網格布點優化前后測點聲級的面積計權均值;μ 和μopt分別為優化前后測點聲級的平均值;σ 和σopt分別為優化前后測點聲級的標準差，且有

式(5)～(7)是針對每類功能區，保證優化前后測點聲級的平均值和面積計權均值的絕對誤差不小于1dB，以及優化前后測點聲級標準差的相對誤差不超過5%. 其中和分別為第i 類功能區優化前后測點聲級的面積計權均值;μi和μi，opt分別為第i 類功能區優化前后測點聲級的平均值;σi和σi，opt分別為第i 類功能區優化前后測點聲級的標準差，且有

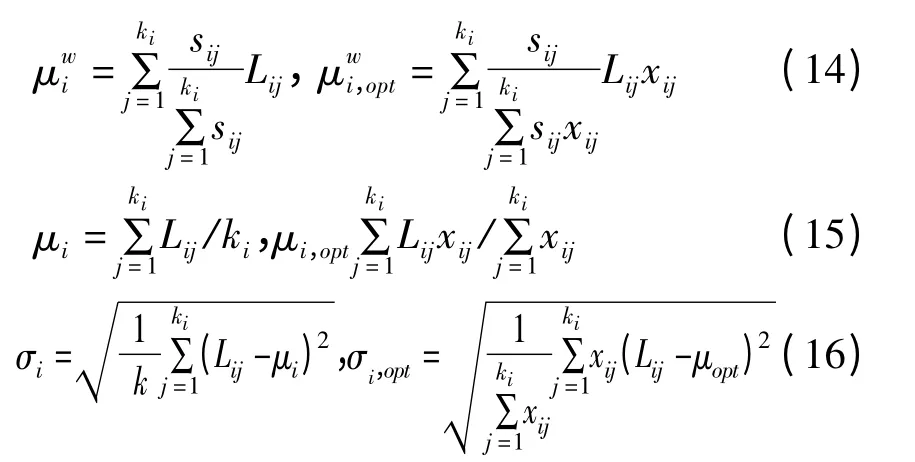
式(8)是為了保證優化前測點較多的功能區，其優化后保留的測點也相對較多，以便于后續的總體評價更為客觀。式(9)約束了每類功能區優化后點數保留范圍。式(10)約束了本問題的設計變量僅可取值為0 或1。

2 改進的并行遺傳算法

本文以粗粒度遺傳算法為基礎，針對其“早熟”和“收斂慢”等主要缺點，提出一系列改進措施，給出一種較優秀的計算智能類算法，即并行混合粒子群免疫算法(PHPSO－IA)。

2.1 改進的自適應交叉、變異算子和多種群演化

2.1.1 自適應交叉、變異

自適應交叉、變異算子在求解非線性和多目標優化問題中的性能不錯，但在這種算子操作下最大適應度個體的交叉、變異概率為零，這在演化初期階段時會使進化過程顯得緩慢。為避免該算法早熟收斂的可能性發生，當個體適應值接近或等于群體最大適應值時，應使得該個體仍有一定的交叉和變異概率，為此本文給出了以下改進的自適應交叉、變異算子，見式(17)和(18)所示。其中，k1，k2，k3，k4為常數，且有0 ＜k1，k2，k3，k4≤1.0，k1＜k3，k2＜k4。

2.1.2 子群體的分類和多種群演化

本文將并行遺傳算法的子群體劃分為四個類型，其參數特征見表1.Ⅰ類子群體的初始個體適應度最小，高的Pc，Pm使它更易探測到新的解空間，從而增大探測到最優個體的可能性，克服過早收斂。Ⅲ類子群體的Pc，Pm相對較小，其群體初始個體的適應度相對較大，因此使它更易保持個體的穩定性，其作用在于強化局部搜索。Ⅱ類子群體的Pc和Pm位于上述兩類子群體之間，且其初始個體的適應度也介于Ⅰ、Ⅲ類群體的初始個體適應度之間。Ⅳ類子群體稱為“保留”子群體，它的初始群體由適應度最大的一些個體組成，并在進化過程中保存前三類種群進化得到的優秀個體，使之不遭受破壞，同時其自身也在進化，其Pc，Pm是四種子群體中最小的，其目的在于保持優秀個體的穩定性和多樣性。算法開始運行時，將隨機初始化生成的個體按適應度的大小進行排序，適應度最大的一些個體分配給Ⅳ類子群體，較大的分配給Ⅲ類子群體，最小的分配給Ⅰ類子群體，其余的分配給Ⅱ類子群體。上述四種類型的群體，每種類型的子群體數可以是一個也可以是若干個。另外，各子群體的規模可以相同也可以不同，應依實際問題而定［9，10］。

表1 各類子群體的參數特征

2.2 并行混合粒子群免疫算法

將生物免疫系統的若干特征引入改進的并行混合遺傳算法，參照免疫記憶功能，將Ⅳ類“保留”子群體對應于記憶細胞庫，稱為“記憶”子群體。模擬免疫系統記憶細胞庫更新和接種過程，給出如下的子群體間信息交換策略:在指定的遷移周期，將Ⅰ、Ⅱ、Ⅲ類各子群體的當前最優個體復制到記憶子群體中，進行記憶子群體更新;同時從記憶子群體中分別選取若干個體遷移到Ⅰ、Ⅱ、Ⅲ類的各子群體中，替換掉它們的較差個體，稱之為接種高效抗體，這種遷移策略可以加快算法的收斂。同時，算法進化到一定的代數(Km的倍數)之后，將所有子群體的個體歸并排序，再按適應度的大小將個體重新分配到相應的各子群體中去。

2.3 基于粒子群優化的個體PSO 更新算子

本文提出了平均模式的PSO 更新算子，其基本思想是當前整個群體中的所有粒子根據其個體極值pbest 所對應的適應度值大小進行排序，選取前u 個粒子信息的平均值來修正每個粒子的行動策略，即

2.4 并行混合粒子群免疫算法的實現

將免疫思想和個體PSO 更新算子改進的并行遺傳算法，即得到了本文的并行混合粒子群免疫算法(PHPSO－IA)，算法流程圖如圖1，其中Ke為設定的遷移周期，Km為設定的子群體歸并周期。

需要說明，對于PSO 更新算子，也可考慮設置更新概率pu，僅當rand()＜pu時，才進行個體的PSO 更新。總之，圖1 給出的是算法整體的框架，可在實際計算時根據情況加以適當調整。

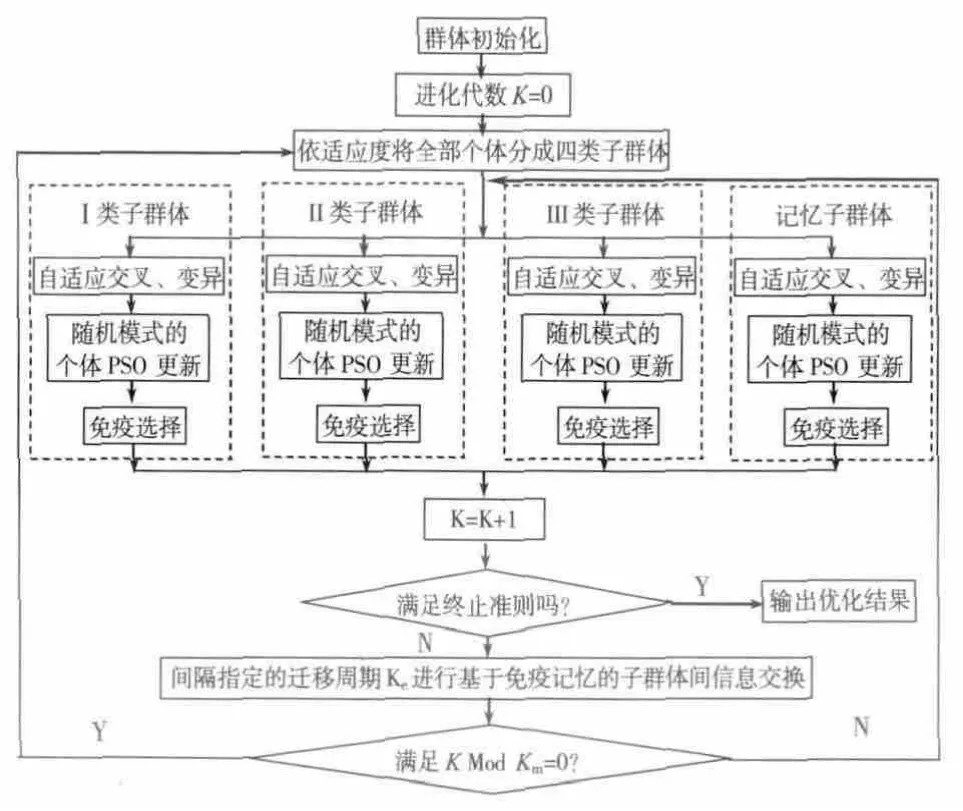
圖1 并行混合粒子群免疫算法的流程圖

3 應用實例

分別采用PGA 和PHPSO － IA 求解該問題，最大進化代數選為1500，每種算法分別運算20次，計算結果的統計對比見表2，兩算法求得的最佳解見表3。

表2 計算結果統計對比

由表2 可以看出，PGA 的平均優化結果為49.00，而PHPSO －IA 的平均優化結果為37.95，后者比前者的測點總數相對減少了(49. 00 －37.95)/49.00 × 100 %=22.55 %. 若從兩種算法20 次運行求得的最佳結果來比較，則PHPSOIA 比PGA 的測點總數相對減少了(43 －36)/43×100 %=16.28 %. PGA 收斂到最優解時，平均進化了679.55 代，而PHPSO －IA 需進化518.60代。兩者相比，后者比前者進化代數減少(679.55－ 518.60)/679.55 ×100 %=23.68 %。在本文的20 次運算中，PHPSO－IA 有兩次在滿足全部約束的條件下，搜索到了最佳目標函數值36. 表3所列的是選用的其中一個最佳解。通過本文給出的算法，可將原來112 個測量點，在滿足整體及各功能區噪聲聲級的統計數字特征相對無明顯改變的情況下，減少到36 個，相對減少了(112 -36)/112 ×100 %=67.86 %，因而可有效地減少日后布點測量時的相關人力和物力的消耗。

表3 兩種算法運行20 次求得的最佳解

4 結 語

本文以城市區域噪聲測量布點優化問題為工程背景，給出了變網格布點測量的思想，并在傳統粗粒度并行遺傳算法(PGA)的基礎上，針對其早熟和收斂慢的兩大缺陷，引入免疫思想自適應交叉、變異的多種群進化和個體PSO 更新算子等策略，對其進行一系列改進，提出了一種并行混合粒子群免疫算法PHPSO-IA。該算法可用于求解連續型和離散型兩類問題。通過和PGA 求解各種算例的計算結果對比可知，該算法是可行的和有效的，其性能確實優于傳統的并行遺傳算法。

［1］沈伋，韓麗川，呂繼淮. 并行遺傳算法在機載寬頻帶天線罩設計中的應用研究［J］. 宇航學報，2005，26(2):158 -161.

［2］SAKAWA M，KATO K，USHIRO S. Operational planning of district heating and cooling plants through genetic algorithms for mixed 0 -1 linear programming［J］. European Journal of Operational Research，2002，137(3):677 -687.

［3］LI G Q，ZHAO H L，TENG H F，et al. An improved parallel hybrid genetic algorithm and its application to layout design［C］. Proceedings of the International conference on Manufacturing Automation，Wuhan，China，2004:295 -302.

［4］劉峻，滕弘飛，屈福政. 人機交互遺傳算法的人機界面［J］. 大連理工大學學報，2005，45(1):58 -63.

［5］SUN Y，ZHANG L，GU X. A hybrid co -evolutionary cultural algorithm based on particle swarm optimization for solving global optimization problems［J］. Neurocomputing，2012，98:76 -89.

［6］NICKABADI A.，EBADZADEH M. M.，and SAFABAKHSH R. A novel particle swarm optimization algorithm with adaptive inertia weight［J］. Applied Soft Computing Journal，2011，11(4):3658 -3670.

［7］BOUDISSA E，BOUNEKHLA M. Genetic algorithm with dynamic selection based on quadratic ranking applied to induction machine parameters estimation［J］. Electr.Power Compon. Syst，2012，40(10):1089 -1104.

［8］SATHEESH K R，ASOKAN P，KUMANAN S. An artificial immune system-based algorithm to solve linear and loop layout problems in flexible manufacturing systems［J］. Int. J. Prod. Dev，2010，10(1):165 -179.

［9］趙鳳強. 城市環境噪聲問題的相關理論方法及應用［D］. 大連:大連理工大學，2005.

［10］ZHAO F-q，LI G -q，YANG C，et al. A human –computer cooperative particle swarm optimization based immune algorithm for layout design［J］. Neurocomputing，2014，1(32):68 -78.