雙向地震激勵的標準化彈塑性位移反應譜

王 豐，王楠楠，張振楠，許海軍

(大連民族學院 土木建筑工程學院，遼寧 大連116605)

近年來，隨著基于性能抗震設計理念的提出，Pushover 分析方法得到了迅速的發展。由于Pushover 理論是建立在等效單自由度系統假設的基礎上，所以可以將其與彈塑性位移譜結合以估算結構位移反應。目前，彈塑性位移譜的研究主要圍繞著強度折減系數展開，很多學者給出了強度折減系數與周期、延性系數的關系［1-3］。有些學者直接通過統計分析建立非線性與線彈性單自由度系統的最大位移關系［4］。一些學者還考慮了P-Δ 效應對彈塑性位移譜的影響［5］。經過一定的研究積累，很多學者對彈塑性位移譜的研究進行了總結與評價［6-7］。然而，彈塑性位移譜的研究幾乎都是以單向地震激勵下的單自由度系統模型為前提，沒有考慮平面外的影響。以往的震害分析及研究表明，結構在多維地震作用下會形成非線性反應的空間耦合作用。所以僅考慮地震的單向水平激勵或按等效單自由度系統來計算分析結構的非線性反應不能準確反映實際情況。為此，文章提出考慮雙向地震激勵的標準化彈塑性位移反應譜理論，根據選取的地震動記錄分析了不同場地、延性系數和兩主軸方向周期比對譜值的影響。

1 基本原理

1.1 單質點雙自由度系統的運動方程

設一個單質點系統，它在相互垂直的兩水平主軸(x 和y)方向上具有雙向自由度，沿兩主軸方向同時承受雙向地震動激勵，運動方程為:

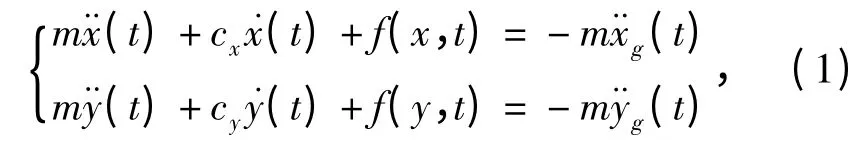
式中，m 為系統的質量;cx和cy為系統沿x 和y 方向阻尼系數;x(t)和y(t)為兩方向的位移反應;f(x，t)和f(y，t)為兩方向的恢復力。假定此單質點雙自由度系統的恢復力模型為二維屈服面模型［8］，可以表示為:

式中，fx，yie和fy，yie為兩主軸方向對應的單自由度系統的屈服力。定義加載、卸載準則為:當F(f(x，t)，f(y，t))＜1.0 時表示處于彈性狀態;當F(f(x，t)，f(y，t))=1.0 時發生了側向力增量(△f(x，t)，△f(y，t))后，有兩種不同反應，一是力(f(x，t)，f(y，t))保持在屈服面上，這時有新的塑性變形增量(△Dx，△Dy)產生，這種情況稱為加載;若力(f(x，t)，f(y，t))由屈服退回屈服面內，則稱為卸載。

1.2 運動方程的標準化

定義單質點雙自由度系統兩正交方向的強度折減系數為Rx=fx，e，max/fx，yie和Ry=fy，e，max/fy，yie，其中fx，e，max和fy，e，max為兩主軸方向對應單自由度系統的最大彈性力，可以分別表示為:

式中，βx和βy為x 和y 方向的地震放大系數反應譜。定義ux(t)=x(t)/xyie和uy(t)=y(t)/yyie，其中xyie和yyie為兩主軸方向對應單自由度系統的屈服位移。將以上定義的關系式帶入式(1)中，整理有:

式中，ωx和ωy為x 和y 方向的圓頻率。在式(4)的求解中，定義μ=max|ux(t)|為系統x 方向的延性系數。由于結構的水平抗力強度是由規范設計譜確定，兩主軸方向的單自由度屈服力比值可以近似表示為fx，yie/fy，yie=a(Tx)/a(Ty)，其中a 為地震影響系數，Tx和Ty分別為系統x 和y 方向的周期，分別等于2π/ωx和2π/ωy。于是可以建立以下關系:

若已知結構x 和y 方向的周期Tx和Ty，通過規范設計譜和式(5)可將式(4)中的Ry用Rx的函數形式替代。

1.3 標準化位移譜模型

在雙向地震動i 的激勵下，系統x 方向的最大的彈性位移和塑性位移分別表示為De，i和Dp，i。結合式(4)和(5)進行計算，若確定某一μ 值，通過迭代可以得到一強度折減系數值Rx，i。根據μ和Rx，i的定義有如下關系:

取多組雙向地震激勵進行計算，然后對式(6)兩側同時取數學期望，進一步推導可以得到以下關系［9］:

式中，由于Sde與Sdp是比值關系，可以約去統計平均中不同地震峰值加速度的影響，所以Sdp和Sde可以分別表示為不同雙向地震激勵得到的Dp，i和De，i的平均值。于是可以表示為x 方向的強度折減系數設計譜。根據彈性位移譜和彈性加速度譜的關系，并用βx·max||替代彈性加速度譜，可以得到系統x 方向的統計平均的標準化彈塑性位移譜公式:

式中，Sdp，n為x 方向統計平均的標準化彈塑性位移譜。Sdp，n是按每條地震波激勵下的彈塑性位移譜Sdp除以相應的地震峰值加速度max||(即標準化)后，再取平均值得到。這種標準化的目的是在建立統計平均譜的過程中可以不用考慮峰值加速度的影響。本文即通過公式(8)、(4)和(5)建立等延性的標準化彈塑性位移譜。

2 標準化彈塑性位移譜分析

2.1 雙向地震記錄

按硬土(Vs=360 -750 m/s)、中等土(Vs=180 -360 m/s)和軟土(Vs＜180 m/s)三類場地分別選擇34 組、35 組、20 組，共89 組(178 條)雙向地震記錄，分別對應USGS 中的B、C 和D 類，詳見文獻［10］。選取的地震記錄滿足如下原則:(1)震級在6 級以上;(2)斷層距在15km ～45km 之間;(3)每組雙向地震記錄中，至少有一條加速度峰值在0.1g 以上。

2.2 標準化彈塑性位移譜

三類場地下周期比η=1 時(定義η=Ty/Tx)的等延性系數標準化位移譜如圖1。分析圖1 可知:(1)三類場地下的標準化位移譜均為逐漸上升的趨勢。其中，硬土和中等土場地的上升較為平緩，為拋物線型，標準化的位移譜值也較小;而軟土場地的上升比較急劇，近似為線性上升，譜值明顯比前兩者大。(2)在硬土場地和軟土場地，隨著延性系數μ 的增大標準化位移譜值逐漸增大，相比較，在軟土場地下此特點更為明顯;在中等土場地，不同延性系數的標準化位移譜的譜值差別不大，規律性不明顯。

為了分析系統兩主軸方向周期比η 對譜值的影響，設θ=Sdp，n(η=某周期比)/Sdp，n(η=1)。于是，可以通過比值θ 以η=1 為基準分析周期比對標準化位移譜的影響。由于篇幅原因，僅以延性系數μ=4 為例，給出了三類場地下η=0.4、0.67、1.5、2.5 所對應的Sdp，n與η=1 所對應Sdp，n的比值譜，即θ 譜如圖2。通過分析可知:(1)三類場地下總的特點是θ(η=0.67 和1.5)比θ(η=0.4 和2.5)更接近1，在短周期時θ(η=0.4 和2.5)偏離1 比較明顯。說明單質點雙自由度系統的兩主軸方向周期的相對差值越大，對標準化位移譜的影響越明顯。(2)隨著延性系數的增大，此影響有增大的趨勢。

圖1 標準化的彈塑性位移譜(η=1)

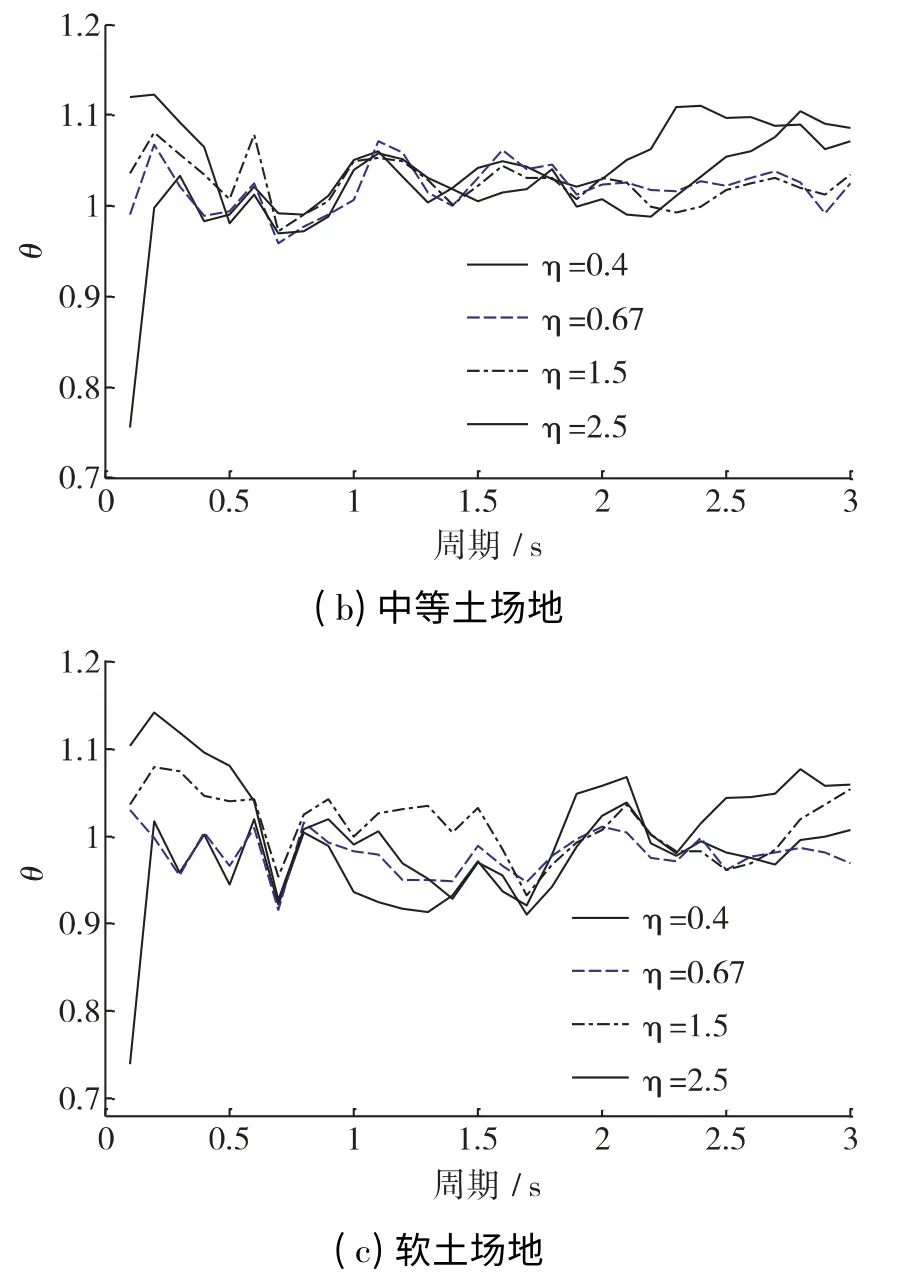
圖2 周期比對標準化彈塑性位移譜的影響圖

3 結 論

提出了考慮雙向地震激勵的標準化彈塑性位移譜理論。假設單質點雙自由度系統的彈塑性特性滿足二維屈服面函數，選取89 組雙向地震記錄作為系統的雙向激勵，建立了統計平均的等延性系數標準化位移譜，分析了不同場地、延性系數和周期比對譜值的影響。通過分析得出:

(1)場地譜型特征:硬土和中等土場地譜型呈拋物線上升趨勢，軟土場地譜型呈近似線性上升趨勢。硬土場地的譜值最小，中等土場與硬土場地的譜值比較接近，軟土場地的譜值明顯大于前兩者。

(2)延性系數的影響:在硬土和軟土場地下，隨延性系數增大譜值有逐漸增大的趨勢，而在中等土場地下，此特點不明顯。

(3)周期比的影響:兩主軸方向周期比對標準化位移譜具有一定的影響，并且隨著延性系數的增大，影響有增大趨勢。

［1］VIDIC T，FAJFAR P，FISHINGER M. Consistent inelastic design spectra:strength and displacement［J］.Earthquake Engineering and Structural Dynamics，1994，23:507 -521.

［2］徐福江，錢稼茹.常延性系數彈塑性位移譜及其應用［J］. 工程力學，2007，24(6):15 -20.

［3］BOZORGNIA Y，HAEHEM M M，CAMPBELL K W.Ground motion prediction equation for inelastic response spectra［J］. Earthquake Spectra，2010，26(1):1 -23.

［4］翟長海，李爽，謝禮立，等. 鋼筋混凝土規則框架結構非彈性位移比譜研究［J］. 工程力學，2009，26(9):80 -86.

［5］ZHAI Changhai，LI Ning，MA Yuhong. P-Δ effect on inelastic displacement ratio spectra for inelastic structures［J］. Journal of Harbin Institute of Technology，2011，18(1):107 -112.

［6］TONG G S，ZHAO Y F. Inelastic yielding strength demand coefficient spectra［J］. Soil Dynamic and Earthquakes Engineering，2008，28:1004 -1013.

［7］BOZORGNIA Y，HAEHEM M M，CAMPBELL K W.Deterministic and probabilistic predictions of yield strength and inelastic displacement spectra［J］. Earthquake Spectra，2010，26(1):25 -40.

［8］王東升，李宏男，王國新.雙向地震動作用彈塑性反應譜研究［J］. 大連理工大學學報，2005，45(2):248 -254.

［9］王豐，李宏男，伊廷華.雙向地震作用下等延性強度折減系數反應譜研究［J］.振動工程學報，2009，22(2):193 -199.

［10］王豐，李宏男.雙向地震作用下等延性系數的標準化滯回能量反應譜［J］. 地震工程與工程振動，2013，33(6):178 -186.