基于離散GM模型和指數(shù)平滑模型組合的統(tǒng)計(jì)預(yù)測(cè)方法
陳有為
(西安郵電大學(xué) 經(jīng)濟(jì)與管理學(xué)院,西安710121)
1 離散GM模型和指數(shù)平滑模型構(gòu)建
1.1 離散GM(1,1)模型
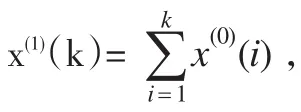
根據(jù)離散GM(1,1)模型的基本原理,設(shè)定含參數(shù)的擬合模型如下:

其中,參數(shù)β1和β2由最小二乘估計(jì)得到,計(jì)算方法為:

1.2 指數(shù)平滑模型
指數(shù)平滑模型是一種在數(shù)值加權(quán)平均的基礎(chǔ)上進(jìn)行預(yù)測(cè)的模型,其基本原理是:首先對(duì)原始數(shù)據(jù)進(jìn)行平滑處理,然后根據(jù)處理后的新數(shù)值,經(jīng)過(guò)估計(jì)參數(shù)進(jìn)行模型擬合,再用該模型進(jìn)行數(shù)值預(yù)測(cè)。一般而言,指數(shù)平滑模型中的加權(quán)系數(shù)根據(jù)幾何級(jí)數(shù)遞減,所有權(quán)數(shù)的和為1。指數(shù)平滑模型思路簡(jiǎn)單,計(jì)算方法通俗易懂,預(yù)測(cè)結(jié)果也相對(duì)較穩(wěn)定,不僅適用于短期序列的預(yù)測(cè),還適用于中期序列預(yù)測(cè)。本文采用三次指數(shù)平滑模型進(jìn)行預(yù)測(cè),其基本計(jì)算公式如下:

1.3 組合預(yù)測(cè)模型構(gòu)建
灰色系統(tǒng)模型的一大優(yōu)點(diǎn)在于不要求通過(guò)足夠的數(shù)據(jù)建立模型,因此可以將原有數(shù)據(jù)序列的末端數(shù)據(jù)根據(jù)不同步長(zhǎng)分別構(gòu)建離散GM(1,1)模型,然后將所有的單項(xiàng)模型分別和指數(shù)平滑模型進(jìn)行組合,再?gòu)闹羞x擇最佳組合模型,從而達(dá)到精確預(yù)測(cè)的效果。
現(xiàn)假設(shè)系統(tǒng)已經(jīng)根據(jù)n個(gè)初始數(shù)據(jù),構(gòu)建了m個(gè)單項(xiàng)的GM(1,1)模型xi(0)(k)(其中,i=1,2,…,m;k=1,2,…,n),于是,根據(jù)這些單項(xiàng)模型,結(jié)合指數(shù)平滑模型,可構(gòu)建組合預(yù)測(cè)模型如下:
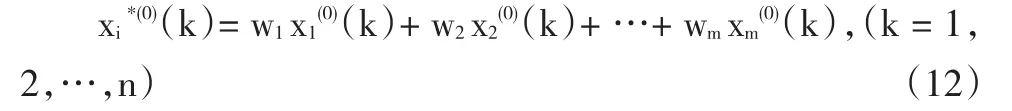
其中,w1,w2,…,wm為待定的組合加權(quán)系數(shù),有w1+w2+…+wm=1。一般可以根據(jù)最大灰色關(guān)聯(lián)系數(shù)的法則對(duì)組合加權(quán)系數(shù)進(jìn)行確定。定義原始數(shù)據(jù)序列{x(0)(k)}與預(yù)測(cè)數(shù)據(jù)序列{xi*(0)(k)}的相關(guān)系數(shù)可進(jìn)行如下計(jì)算:
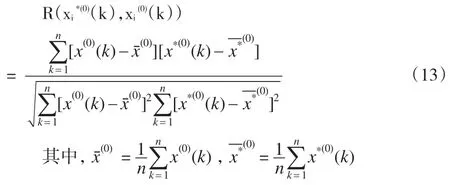
根據(jù)相關(guān)系數(shù)最大值的原則,可以解得式(12)中的權(quán)重系數(shù)wi(i=1,2,…,m)。這個(gè)問(wèn)題歸結(jié)為求式(13)的R(xi*(0)(k),xi(0)(k))的最大值,這是一個(gè)非線性最優(yōu)解問(wèn)題,可通過(guò)非線性規(guī)劃求得。
在解得權(quán)重系數(shù)w*i(i=1,2,…,m)后,組合預(yù)測(cè)模型中的預(yù)測(cè)值xi*(0)(k)可表示為以下線性組合:
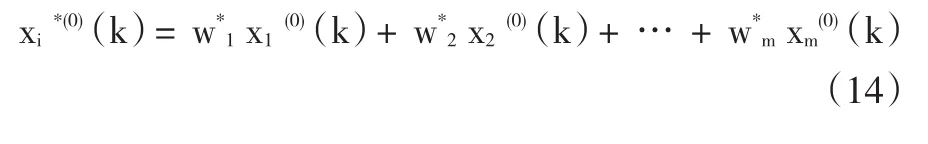
2 組合預(yù)測(cè)模型在實(shí)際統(tǒng)計(jì)領(lǐng)域中的運(yùn)用
為了檢驗(yàn)離散GM模型與指數(shù)平滑模型組合后的改進(jìn)模型在實(shí)際統(tǒng)計(jì)運(yùn)用中的有效性和預(yù)測(cè)精度,首先選取我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量進(jìn)行預(yù)測(cè),時(shí)間跨度為1991~2012年。其中,城鎮(zhèn)居民家庭人均購(gòu)買鮮菜數(shù)量的統(tǒng)計(jì)數(shù)據(jù)如表1所示。
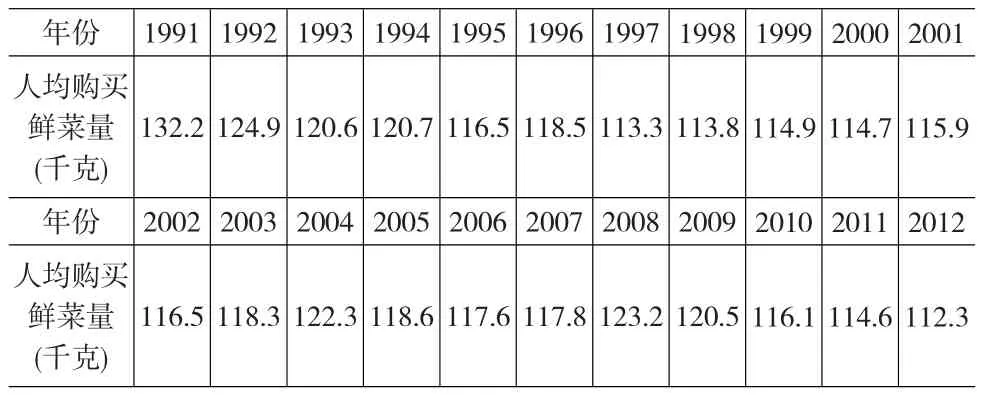
表1 1991~2012年我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜數(shù)量的統(tǒng)計(jì)數(shù)據(jù)
首先,根據(jù)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜數(shù)量的原始數(shù)據(jù),構(gòu)建三次指數(shù)平滑模型。這里,首先需對(duì)加權(quán)系數(shù)λ進(jìn)行確定。根據(jù)最小二乘原則,選定初始值 S0(1)=S0(2)=S0(3)=125.9,確定加權(quán)系數(shù)λ的值為 0.65。于是,可根據(jù)式(6)~式(11),計(jì)算得到:

根據(jù)以上的三次平滑預(yù)測(cè)模型,可以計(jì)算2003~2012年我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜數(shù)量的擬合值,結(jié)果如表2所示。
然后,根據(jù)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜數(shù)量的原始數(shù)據(jù),構(gòu)建離散GM(1,1)模型。由前面的分析,這里分別根據(jù)2002~2012年的數(shù)據(jù)序列、2003~2012年的數(shù)據(jù)序列、2004~2012年的數(shù)據(jù)序列和2005~2012年的數(shù)據(jù)序列,構(gòu)建4個(gè)離散GM(1,1)模型,然后分別將這四個(gè)離散GM(1,1)模型與三次指數(shù)平滑模型進(jìn)行組合,并根據(jù)相關(guān)系數(shù)值最大的規(guī)則選擇最優(yōu)組合預(yù)測(cè)模型。
計(jì)算可得,通過(guò)2003~2012年的數(shù)據(jù)序列建立的組合預(yù)測(cè)模型的相關(guān)系數(shù)達(dá)到0.762,是四個(gè)組合預(yù)測(cè)模型中最高的,因此利用2003~2012年數(shù)據(jù)序列建立的離散GM(1,1)模型最為合理。參考式(2)和式(3),并借鑒王豐效(2011)等人的方法,采用最小二乘法對(duì)離散GM(1,1)模型的參數(shù)進(jìn)行估計(jì),結(jié)果為:

根據(jù)該遞推公式,便可得到2003年至2012年我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量的GM(1,1)擬合值,結(jié)果仍如表2所示。
根據(jù)以上三次指數(shù)平滑預(yù)測(cè)模型和離散GM(1,1)預(yù)測(cè)模型,可構(gòu)建組合預(yù)測(cè)模型。根據(jù)式(13),并采用一定的計(jì)算處理,可得到三次指數(shù)平滑預(yù)測(cè)模型和離散GM(1,1)預(yù)測(cè)模型的權(quán)重系數(shù)分別為:

于是,通過(guò)加權(quán)可得到組合預(yù)測(cè)模型下我國(guó)2003年至2012年城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量的預(yù)測(cè)值,結(jié)果仍由表2給出。
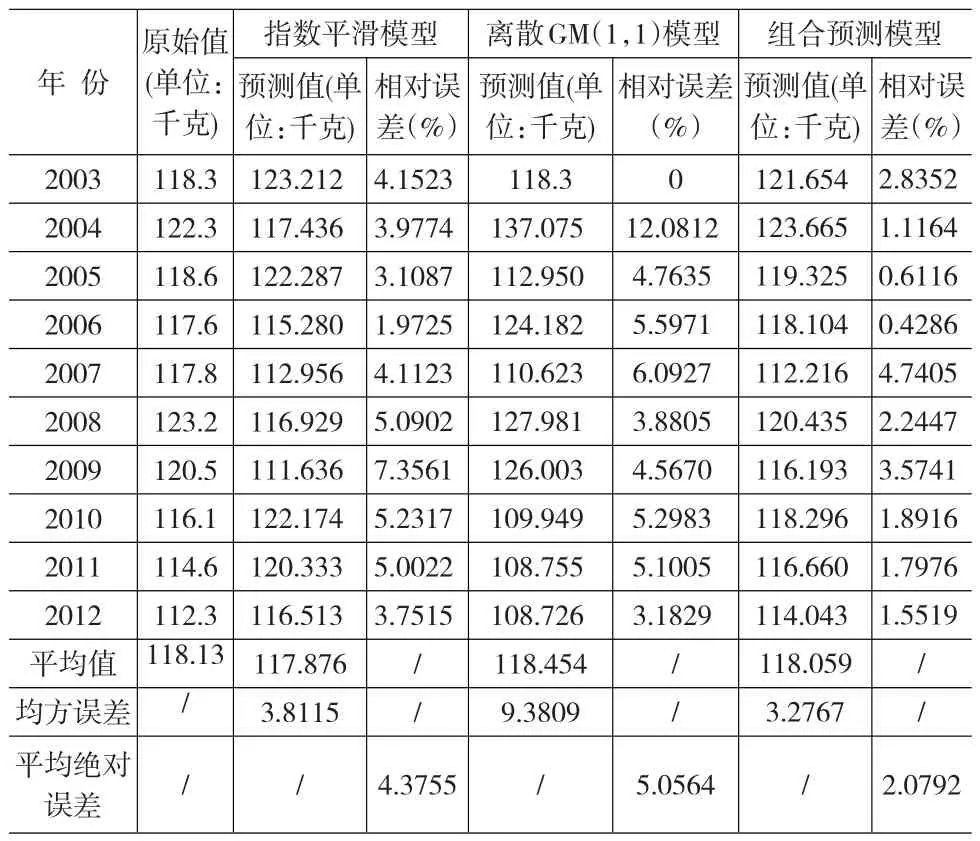
表2 三種預(yù)測(cè)模型的我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量預(yù)測(cè)值
對(duì)比表2中三種預(yù)測(cè)方法得到的結(jié)果可知,由離散GM(1,1)模型與指數(shù)平滑模型的組合模型預(yù)測(cè)結(jié)果的均方誤差低于兩種單項(xiàng)預(yù)測(cè)方法。組合模型預(yù)測(cè)結(jié)果的均方誤差僅為3.2767,而離散GM(1,1)方法預(yù)測(cè)結(jié)果的均方誤差高達(dá)9.3809。從歷年我國(guó)城鎮(zhèn)居民人均蔬菜購(gòu)買量的預(yù)測(cè)誤差來(lái)看,組合預(yù)測(cè)方法得到的各年預(yù)測(cè)誤差普遍低于另外兩種單項(xiàng)預(yù)測(cè)方法,計(jì)算可得,組合預(yù)測(cè)方法得到的平均絕對(duì)誤差值為2.0792,三次指數(shù)平滑模型得到的平均絕對(duì)誤差值為4.3755,離散GM(1,1)模型得到的平均絕對(duì)誤差值為5.0564。
由圖1可清晰地看出,組合預(yù)測(cè)模型對(duì)我國(guó)城鎮(zhèn)居民人均蔬菜購(gòu)買量的預(yù)測(cè)值最接近原始值,而離散GM(1,1)的預(yù)測(cè)波動(dòng)性最高。由此可見,組合預(yù)測(cè)模型的預(yù)測(cè)精度要高于三次指數(shù)平滑模型和離散GM(1,1)模型。
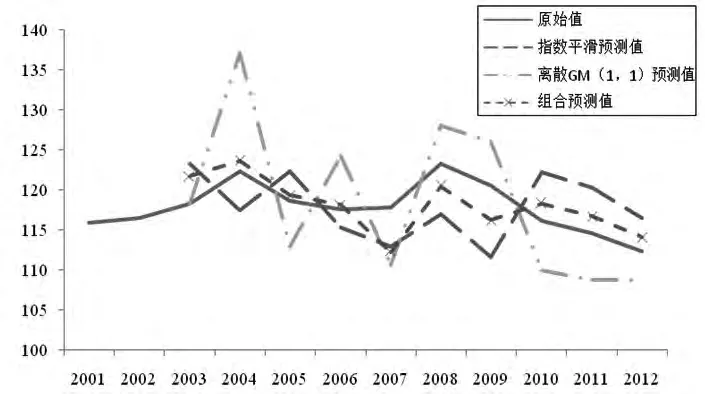
圖1 三種預(yù)測(cè)模型對(duì)我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量預(yù)測(cè)結(jié)果的比較(單位:千克)
3 結(jié)論
由于指數(shù)平滑預(yù)測(cè)模型對(duì)樣本數(shù)據(jù)的條件要求較高,特別是需要大量的時(shí)間序列,而離散GM(1,1)預(yù)測(cè)模型雖然不要求提供大量的原始數(shù)據(jù),但在實(shí)際過(guò)程中對(duì)離散的數(shù)據(jù)預(yù)測(cè)效果并不是很好,為此本文通過(guò)加權(quán)方法,設(shè)計(jì)了一種由三次指數(shù)平滑預(yù)測(cè)模型和離散GM(1,1)預(yù)測(cè)模型組合的預(yù)測(cè)模型,并選取了我國(guó)城鎮(zhèn)居民家庭人均購(gòu)買鮮菜量的實(shí)例進(jìn)行預(yù)測(cè)和比較。由實(shí)證結(jié)果可知,由組合預(yù)測(cè)模型得到的預(yù)測(cè)結(jié)果在預(yù)測(cè)精度上優(yōu)于三次指數(shù)平滑預(yù)測(cè)模型和離散GM(1,1)預(yù)測(cè)模型,因此這種組合預(yù)測(cè)模型可能比單項(xiàng)的預(yù)測(cè)模型更具有可行性。
[1]Tang H W V,Yin M S.Forecasting Performance of Grey Prediction for Education Expenditure and school Enrollment[J].Economics of Education Review,2012,31,(4).
[2]Bonsdorff H.A comparison of the orDinary and a Varying Parameter Exponential Smoothing[J].Journal of Applied Probability,1989,(27).
[3]Chang,S C Wu J Lee C T.A Study on the Characteristics of Grey Prediction[R].Proc.of the 4th Conference on Grey Theory and Applications,1999.
[4]Su Z B,An J L.Application of Grey Metabolic GM(1.1)Model in Prediction of per Capita Net Income of Rural Residents[J].Journal of Xi.an University of Arts&Science(Nat Sci Ed),2009,12(4).
[5]王豐效.改進(jìn)的GM(1,1)冪模型及其參數(shù)優(yōu)化[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2011,27(6).
[6]陳露,張凌霜.基于初值修正的組合灰色Verhulst模型[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí),2010,40(11).

