專業(yè)市場(chǎng)價(jià)格指數(shù)基期調(diào)整研究
孫 艷,舒 佩
(華南理工大學(xué) 經(jīng)濟(jì)與貿(mào)易學(xué)院,廣州 510006)
0 引言
對(duì)于專業(yè)市場(chǎng),許多學(xué)者給出了自己的理解,鄭勇軍(2003)把專業(yè)市場(chǎng)闡述為以現(xiàn)貨批發(fā)為主,集中交易某一類商品或若干具有較強(qiáng)互補(bǔ)性和互替性商品的場(chǎng)所,是一種大規(guī)模集中交易的坐商式的市場(chǎng)制度安排;王勇(2013)定義專業(yè)市場(chǎng)是一種規(guī)模化、專業(yè)化的交易組織。本文認(rèn)為專業(yè)市場(chǎng)是指積聚同類產(chǎn)品進(jìn)行的交易、流通和配送的場(chǎng)所,是一種專門性商品批發(fā)市場(chǎng)。
目前,國(guó)內(nèi)外對(duì)于基期調(diào)整的研究還是相對(duì)缺乏,其中Stanley K.S,Terry Sincich(1990)在對(duì)人口指數(shù)的計(jì)算中研究了基期適用性問題,他們認(rèn)為指數(shù)的基期時(shí)間越長(zhǎng),指數(shù)越能反映現(xiàn)實(shí)趨勢(shì)的變化;魏小真(2001)在探討變更國(guó)內(nèi)生產(chǎn)總值的基期中提出基期的時(shí)間過長(zhǎng)往往會(huì)引起現(xiàn)價(jià)與不變價(jià)之間背離過大,增長(zhǎng)速度和經(jīng)濟(jì)結(jié)構(gòu)不能準(zhǔn)確地反映當(dāng)期的實(shí)際情況,建議每5年變換一次GDP核算的基期價(jià)格。而幾乎沒有文獻(xiàn)專門研究專業(yè)市場(chǎng)價(jià)格指數(shù)基期變換的問題。
通常來講,一般性指數(shù)的基期變換周期較長(zhǎng),如CPI的基期10年來僅變更過一次;而對(duì)于專業(yè)市場(chǎng)價(jià)格指數(shù)而言,由于市場(chǎng)價(jià)格波動(dòng)較大,長(zhǎng)周期的變換基期無法保證指數(shù)的精確,這就要求我們及時(shí)調(diào)整基期價(jià)格以適應(yīng)專業(yè)市場(chǎng)價(jià)格的變化,那么何時(shí)調(diào)整專業(yè)市場(chǎng)價(jià)格指數(shù)的基期則是本文的研究重點(diǎn)。
1 理論模型及數(shù)據(jù)說明
1.1 理論假設(shè)
對(duì)于專業(yè)市場(chǎng)價(jià)格指數(shù)基期變更問題,假說如下:(1)專業(yè)市場(chǎng)產(chǎn)品價(jià)格與指數(shù)分布為正態(tài)分布;(2)專業(yè)市場(chǎng)兩個(gè)基期價(jià)格的變動(dòng)率與兩個(gè)基期計(jì)算出的價(jià)格指數(shù)之間的變動(dòng)率的關(guān)系為線性;(3)如果基期變化正確,則兩個(gè)基期之間的變動(dòng)率(X)和以這兩個(gè)基期計(jì)算出的價(jià)格指數(shù)之間的變動(dòng)率(Y)構(gòu)成的回歸方程的系數(shù)在整個(gè)專業(yè)市場(chǎng)以基期價(jià)格變動(dòng)率和指數(shù)變動(dòng)率構(gòu)成的總體回歸方程系數(shù)置信區(qū)間之內(nèi)。
1.2 模型設(shè)置
根據(jù)上訴假說,本文對(duì)價(jià)格指數(shù)變動(dòng)率和基期價(jià)格變動(dòng)率之間采取線性回歸方程進(jìn)行分析。基本模型設(shè)定如下:

式(1)中,Y代表因變量?jī)r(jià)格指數(shù)變動(dòng)率,x代表自變量基期價(jià)格變動(dòng)率,a為隨個(gè)體變化的截距項(xiàng),ε為隨機(jī)誤差項(xiàng)。
1.3 數(shù)據(jù)說明
此次分析是以清遠(yuǎn)再生銅市場(chǎng)為例,我們掌握了2007年7月~2012年10月的產(chǎn)品價(jià)格數(shù)據(jù)(包括銷售品種,銷售價(jià)格,銷售量等)和已經(jīng)發(fā)布的44期清遠(yuǎn)再生銅價(jià)格指數(shù)的數(shù)據(jù)。
2 隨機(jī)模擬實(shí)驗(yàn)與實(shí)證檢驗(yàn)
2.1 隨機(jī)模擬實(shí)驗(yàn)
2.1.1 基期價(jià)格分布
清遠(yuǎn)再生銅價(jià)格指數(shù)的基期定為月平均價(jià)格,表1是所有基期價(jià)格的正態(tài)分布檢驗(yàn)結(jié)果,可以看出清遠(yuǎn)再生銅市場(chǎng)的基期價(jià)格滿足正態(tài)分布。
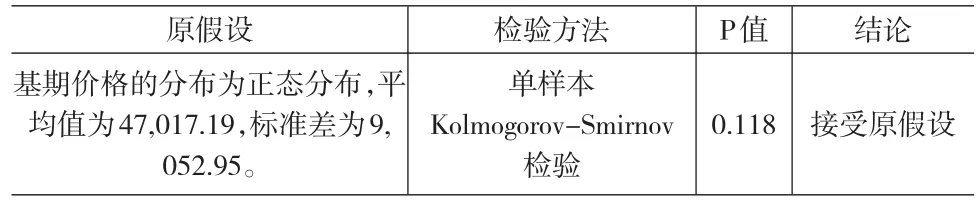
表1 單樣本K-S檢驗(yàn)結(jié)果
2.1.2 生成隨機(jī)數(shù)
如果某隨機(jī)變量服從正態(tài)分布N(α,σ2),按模擬正態(tài)分布算法求出服從標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)數(shù)x,令

那么W即為服從正態(tài)分布N(α,σ2)的隨機(jī)數(shù)。在本問題中,基期價(jià)格服從正態(tài)分布,按照上述算法用R軟件產(chǎn)生70組基期價(jià)格隨機(jī)數(shù),為方便計(jì)算,基期價(jià)格用每一組價(jià)格的中位數(shù)表示,并以隨機(jī)數(shù)計(jì)算相應(yīng)的價(jià)格指數(shù)。
2.1.3 模擬結(jié)果檢驗(yàn)
對(duì)70組基期價(jià)格和指數(shù)隨機(jī)數(shù)進(jìn)行數(shù)據(jù)分析,記基期價(jià)格兩兩之間的變動(dòng)率為X,相對(duì)應(yīng)指數(shù)兩兩之間的變動(dòng)率為Y,用SPSS軟件對(duì)X,Y進(jìn)行線性回歸分析,有如下結(jié)果:

表2 模型匯總
且得出下式:

隨機(jī)模擬結(jié)果初步表明前面的理論假設(shè)和模型設(shè)定可以解釋專業(yè)市場(chǎng)價(jià)格指數(shù)中基期價(jià)格和指數(shù)之間的關(guān)系。
2.2 實(shí)證檢驗(yàn)
我們按照一般性的原則確定了清遠(yuǎn)再生銅價(jià)格指數(shù)的基期,并成功發(fā)布指數(shù)。現(xiàn)在試著通過變換已確定的基期,同時(shí)算出所有變動(dòng)基期相對(duì)應(yīng)的清遠(yuǎn)再生銅價(jià)格指數(shù),以探討基期變化和價(jià)格指數(shù)變化的關(guān)系。
首先從已掌握的基期價(jià)格數(shù)據(jù)(2007年7月~2012年10月)中用等距抽樣的方法選出了不同的基期一共9期,并計(jì)算出了每一期基期相對(duì)應(yīng)的價(jià)格指數(shù)。
因?yàn)槊恳黄诨诙加?8個(gè)代表品價(jià)格,為了方便比較不同基期價(jià)格之間的變動(dòng),采用28個(gè)代表品價(jià)格的中位數(shù)表示每一期基期的價(jià)格,見下表:

表3 9期基期代表品價(jià)格中位數(shù) (單位:元/噸)
數(shù)據(jù)來源:清遠(yuǎn)再生銅交易中心數(shù)據(jù)庫
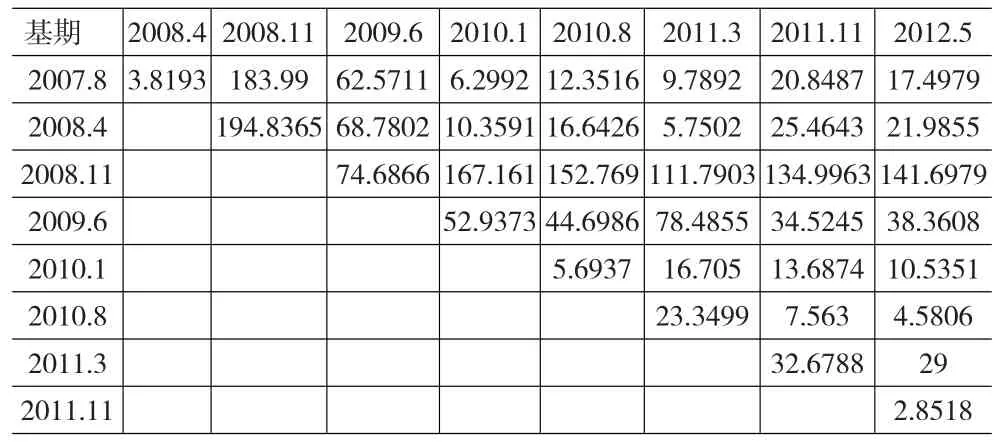
表4 9期基期價(jià)格相互之間上升百分比 (單位:%)
而與之相對(duì)應(yīng)的,我們可以計(jì)算出不同基期對(duì)應(yīng)指數(shù)兩兩之間的下降百分比(公式:;A,B代指不同基期的價(jià)格指數(shù)),以第一期發(fā)布的指數(shù)為例,見下表:

表5 第一期指數(shù)之間下降百分比 (單位:%)
這樣就得到了兩組數(shù)據(jù),一組為基期價(jià)格變動(dòng)的上升百分比,另一組為指數(shù)變動(dòng)的下降百分比,前者為自變量,后者為因變量,二者一一對(duì)應(yīng)。我們用spss軟件對(duì)上述兩組數(shù)據(jù)進(jìn)行分析:
首先做出二者的散點(diǎn)圖,見圖1,可以看到所有的點(diǎn)基本上近似在一條直線的附近,就可以粗略的認(rèn)為價(jià)格指數(shù)變動(dòng)率依賴于基期價(jià)格變動(dòng)率的關(guān)系適合用一元線性模型來表示。
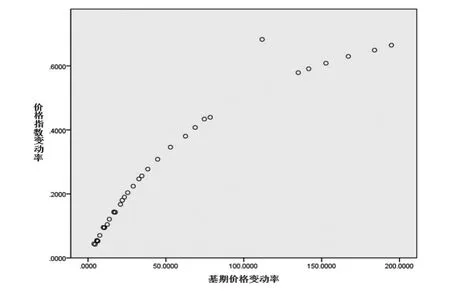
圖1 基期價(jià)格變動(dòng)率和價(jià)格指數(shù)變動(dòng)率的散點(diǎn)圖
然后做兩個(gè)變量的回歸分析,結(jié)果如下:

表6 模型匯總
表6所示的結(jié)果就是對(duì)回歸方程擬合情況的描述,可以看到相關(guān)系數(shù)為0.957,決定系數(shù)R2為0.917(R2表示自變量所能解釋的方差在總方差中所占的百分比),也就是說回歸關(guān)系可以解釋因變量91.7%的變異,這說明模型的效果非常好。
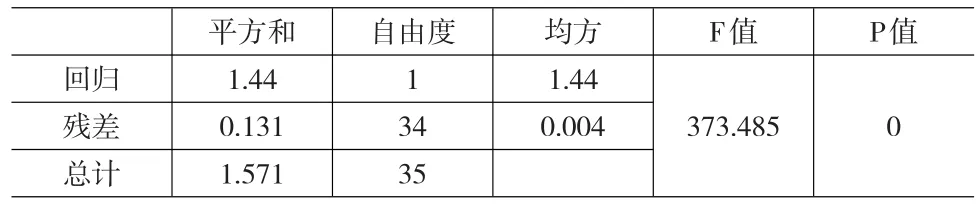
表7 方差分析
表7即為對(duì)模型進(jìn)行方差分析的結(jié)果,F(xiàn)值為362.883,P值小于0.05,所以該模型具有統(tǒng)計(jì)意義,由于只有一個(gè)自變量,也就是說該自變量的回歸系數(shù)是有統(tǒng)計(jì)意義的。

表8 回歸方程的系數(shù)
表8給出了回歸方程中常數(shù)項(xiàng),回歸系數(shù)的估計(jì)值和檢驗(yàn)結(jié)果,由此可以得出如下回歸方程:
價(jià)格指數(shù)變動(dòng)率(下降百分比)=0.0864+0.0035*基期價(jià)格變動(dòng)率(上升百分比),即:

上述回歸方程給出了如下信息:基期價(jià)格每上升一個(gè)百分點(diǎn),價(jià)格指數(shù)就會(huì)下降0.004個(gè)百分點(diǎn)。而后通過計(jì)算分析其它43期指數(shù)變動(dòng)率與基期變動(dòng)率的線性關(guān)系,一共可以得到44個(gè)回歸方程。
以這44期回歸方程的系數(shù)為樣本,采用95%的置信度估計(jì)全部系數(shù)的平均值,用來表示價(jià)格指數(shù)變動(dòng)率和基期變動(dòng)率之見線性關(guān)系的總體情況。首先需要驗(yàn)證基期價(jià)格變動(dòng)率系數(shù)是否滿足正態(tài)分布,用SPSS軟件做K-S檢驗(yàn),結(jié)果顯示其滿足正態(tài)分布,然后做單樣本的T檢驗(yàn),得到:

表9 單個(gè)樣本檢驗(yàn)
這樣在95%的置信度下基期價(jià)格變動(dòng)率系數(shù)的平均值就在0.0034到0.0035之間。
同理,可以求得在95%的置信度下常量的平均值在0.0863到0.0869之間。那么,所得到的總體回歸方程為:

3 結(jié)論
本文通過清遠(yuǎn)再生銅價(jià)格指數(shù)的實(shí)例驗(yàn)證了價(jià)格指數(shù)變動(dòng)率和基期價(jià)格變動(dòng)率存在的線性關(guān)系,說明前文的理論假設(shè)在專業(yè)市場(chǎng)是可以得到證明的。這樣就為專業(yè)市場(chǎng)基期的調(diào)整變換提供了現(xiàn)實(shí)意義的指導(dǎo):以最新收集到的產(chǎn)品價(jià)格作為基期計(jì)算相應(yīng)價(jià)格指數(shù),當(dāng)該價(jià)格指數(shù)與實(shí)際發(fā)布的價(jià)格指數(shù)之間的變動(dòng)率與兩個(gè)基期之間變動(dòng)率構(gòu)成的線性方程系數(shù)不在總體回歸方程系數(shù)置信區(qū)間的時(shí)候,說明應(yīng)該變換原基期。
[1]鄭勇軍.浙江農(nóng)村工業(yè)化中的專業(yè)市場(chǎng)制度研究[J].浙江社會(huì)科學(xué),1998,(6).
[2]王勇,劉傳玉等.專業(yè)市場(chǎng)驅(qū)動(dòng)的區(qū)域增長(zhǎng)路徑與機(jī)制:臨沂模式研究[J].東岳論叢,2013,(5).
[3]Stanley K.Smith,Terry Sincich.The Relationship Between The Length of The Base Period and Population Forecast Errors[J].Journal of The American Statistical Association,1990,(7).
[4]魏小真.關(guān)于國(guó)內(nèi)生產(chǎn)總值核算基期更換的幾個(gè)問題[J].北京統(tǒng)計(jì),2001,(5).
[5]徐國(guó)祥等.統(tǒng)計(jì)指數(shù)理論、方法與應(yīng)用研究[M].上海:上海人民出版社,2011.
[6]孫艷,吳智慧.專業(yè)市場(chǎng)價(jià)格指數(shù)編制理論初探[J].價(jià)格月刊,2012,(5).

