基于灰關(guān)聯(lián)熵的成本預測方法與實證

文 義

（湖南財政經(jīng)濟學院 會計系，長沙 410205）

1 成本預測組合預測模型

設企業(yè)成本歷史數(shù)值為Y={y(1)，y(2)，…，y(n)}，經(jīng)過前期挑選，設選擇了m種單一預測方法來對該成本數(shù)據(jù)Y進行建模，得到m種預測模型，分別記作

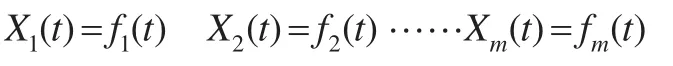
其中t=1，2，3，…n

綜合現(xiàn)有組合預測研究成果可以發(fā)現(xiàn)，組合預測一般可分為基于線性加權(quán)的加權(quán)算術(shù)平均組合預測以及基于非線性加權(quán)組合的幾何加權(quán)組合預測、調(diào)和加權(quán)平均組合預測等幾類，本文將主要考慮線性加權(quán)算術(shù)平均組合預測組合權(quán)重確定方法，下面給出企業(yè)成本的線性加權(quán)算術(shù)平均預測模型:

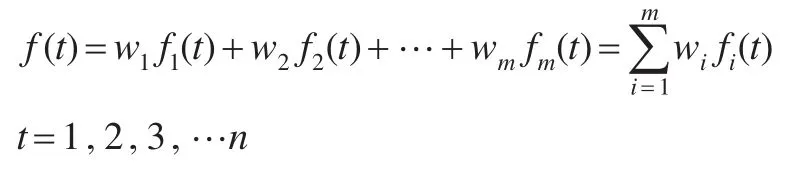
其中w1，w2，…，wm為各種預測方法的組合權(quán)重，一般。

對所建立的預測模型進行精度檢驗是使用模型進行預測的前提，所以在建立任何一種預測模型，必須對所建立模型進行模擬仿真，已對其模擬精度進行檢驗，平均相對誤差是最常用的一種檢驗方法，其計算過程如下：

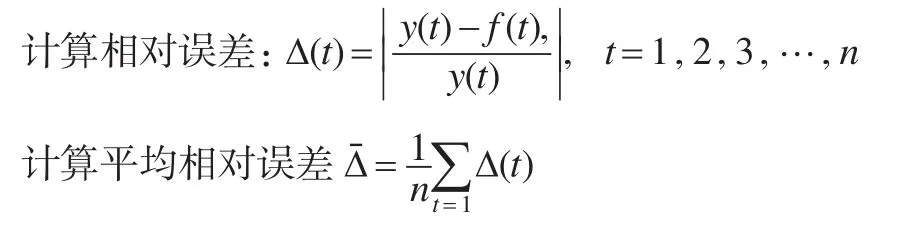
2 基于灰關(guān)聯(lián)熵的組合權(quán)重確定方法研究

灰關(guān)聯(lián)熵不僅能避免灰關(guān)聯(lián)度導致的局部關(guān)聯(lián)傾向和個性信息損失的不足，而且能從整體上描述時間序列之間的相似程度，基于灰關(guān)聯(lián)熵的這些優(yōu)點，本文將基于灰關(guān)聯(lián)熵的原理給出一種確定組合權(quán)重的方法用于成本組合預測模型中的組合權(quán)重確定。

將企業(yè)成本歷史數(shù)值Y={y(1)，y(2)，…，y(n)}作為參考序列，而將到m種預測模型所模擬的時間序列作為比較數(shù)列，從而得到被比較數(shù)列為

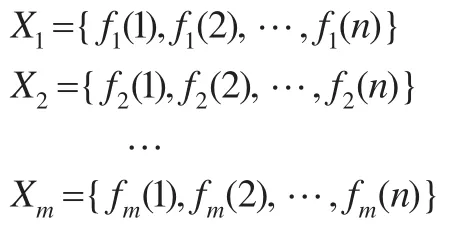
根據(jù)灰關(guān)聯(lián)分析原理，在確定參數(shù)ρ∈(0.1)后可以計算出第k時刻第i種模型所模擬出的時間序列Xi與歷史時間序列Y的灰關(guān)聯(lián)系數(shù)序列為

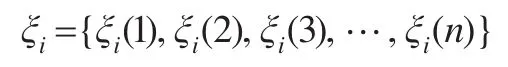
其中

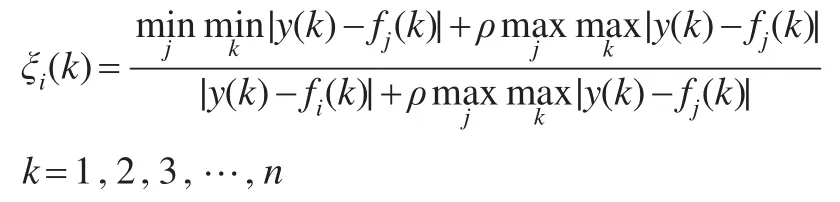
從而可以計算Xi與Y的灰關(guān)聯(lián)度

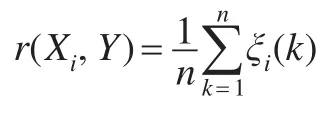
定義1:設灰色內(nèi)涵數(shù)列p={p1，p2，…，pn}滿足，則定義該時間序列的灰熵為：

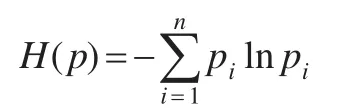
定義2：設時間序列Xi與時間序列Y的灰關(guān)聯(lián)系數(shù)序列為ξi={ξi(1)，ξi(2)，ξi(3)，…，ξi(n)}，對灰關(guān)聯(lián)序列ξi歸一化后得到關(guān)聯(lián)序列為p={p1，p2，…，pn}，則定義時間序列Xi與時間序列Y的灰關(guān)聯(lián)熵為：

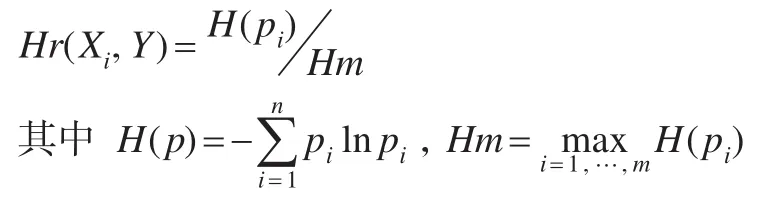
考慮到灰色關(guān)聯(lián)度在刻畫時間序列相似度的過程中存在較多的不足之處，所以在確定多種單一預測方法進行組合預測的過程中，將利用灰關(guān)聯(lián)熵來取代灰關(guān)聯(lián)度，從而確定組合預測的權(quán)重，下面給出具體的基于灰關(guān)聯(lián)熵的組合權(quán)重確定過程。

首先利用灰關(guān)聯(lián)系數(shù)計算方法分別計算出比較序列Xi與參考序列Y的灰關(guān)聯(lián)系數(shù)序列，從而構(gòu)成如下的灰關(guān)聯(lián)系數(shù)矩陣：

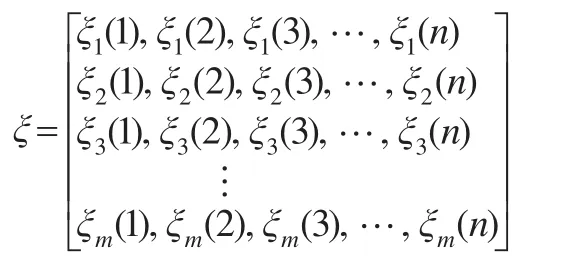
對灰關(guān)聯(lián)系數(shù)矩陣ξ按行歸一化，從而得到歸一化后的灰關(guān)聯(lián)矩陣：

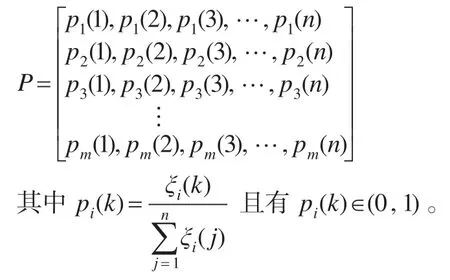
根據(jù)定義2，從而根據(jù)灰關(guān)聯(lián)熵的定義式，從而可以計算出Xi與時間序列Y的灰熵為：

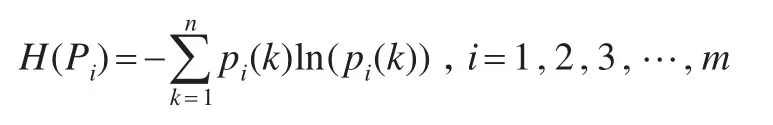
依次計算出各種預測模型所獲得的模擬序列與企業(yè)成本歷史數(shù)值時間序列的灰熵，從而可以得到m個模擬序列與歷史時間序列之間的灰熵序列：

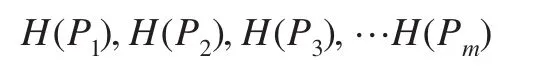
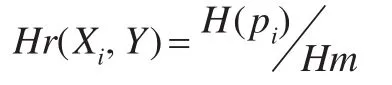
灰關(guān)聯(lián)熵主要描述的是時間序列之間的接近程度，灰關(guān)聯(lián)熵越大，則表明該兩個時間序列之間的接近程度越大，而根據(jù)組合預測原理來分析，一般來說，模擬時間序列與歷史時間序列越接近，則表示該預測方法的精度越高，從而在對其進行組合加權(quán)的過程中，應該賦予較大的權(quán)重，基于這樣的原理，則關(guān)于組合權(quán)重可以通過關(guān)聯(lián)熵來確定，從而得到基于灰關(guān)聯(lián)熵的組合預測權(quán)重確定公示為：

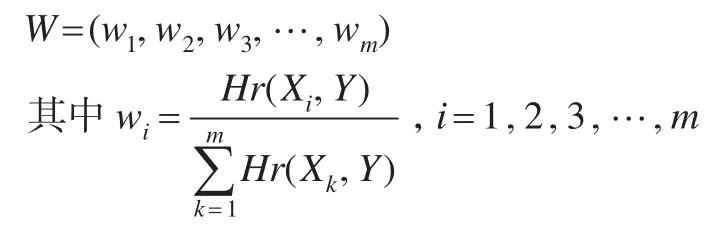
3 基于灰關(guān)聯(lián)熵的成本預測實證分析

為了說明本文所建立的基于灰關(guān)聯(lián)熵的組合權(quán)重確定方法能有效提高組合預測精度，下面我們采用本文所建立的方法來確定組合權(quán)重，并與單一預測方法的預測精度進行對比分析，檢驗本方法的可行性和有效性。針對企業(yè)最近十個月的成本數(shù)據(jù)作為歷史時間序列，并利用該數(shù)據(jù)來預測后期的企業(yè)成本數(shù)量，在單一預測模型的選擇過程中，可以選擇GM（1，1）模型、回歸預測，三次指數(shù)平滑進行預測，并利用灰關(guān)聯(lián)熵來確定組合權(quán)重，從而對比分析組合預測提高預測精度的有效性。

采集該企業(yè)最近十個月的經(jīng)營成本數(shù)據(jù)為（單位：十萬元）：

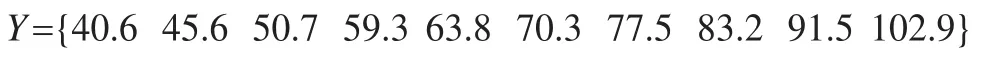
對該歷史數(shù)據(jù)利用灰色預測模型GM（1，1）進行建模，并對其進行數(shù)值模擬，從而得到利用灰色預測模型得到的模擬經(jīng)營成本為：

計算利用灰色預測模型建模得到的模擬數(shù)值的平均相對誤差為：

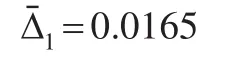
對該經(jīng)營成本數(shù)據(jù)作圖，可以得到該經(jīng)營成本數(shù)據(jù)的變化趨勢如圖1所示。

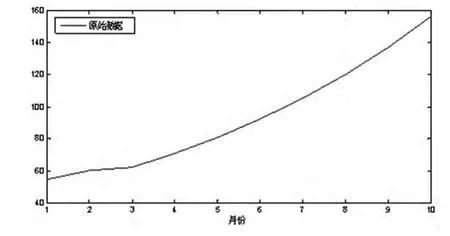
圖1 經(jīng)營成本數(shù)據(jù)變化趨勢圖

通過圖1可以看出，該經(jīng)營成本呈線性變化，所以可以采用線性回歸預測模型建模，并利用該回歸預測模型進行數(shù)值模擬，得到模擬經(jīng)營成本：

計算利用回歸預測模型建模得到的模擬數(shù)值的平均相對誤差為：

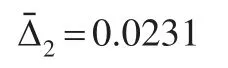
對經(jīng)營成本利用三次指數(shù)平滑預測模型進行建模，在選擇平移參數(shù)α=0.2的情況下進行數(shù)值模擬得到經(jīng)營成本為：

計算利用三次指數(shù)平滑預測模型建模得到的模擬經(jīng)營成本的平均相對誤差為：

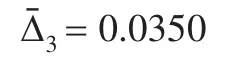
對三種單一預測方法利用本文所給出的基于灰關(guān)聯(lián)熵的組合權(quán)重確定方法確定出四種單一預測模型的組合權(quán)重。首先計算出各單一預測方法模擬經(jīng)營成本與歷史經(jīng)營成本的灰關(guān)聯(lián)系數(shù)矩陣：

對其按行歸一化后得到：

從而計算出模擬經(jīng)營成本與歷史經(jīng)營成本之間的灰熵序列：

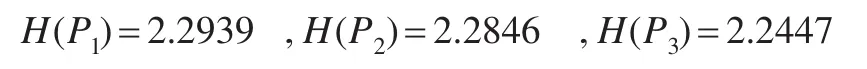
對其歸一化后得到的組合權(quán)重向量：

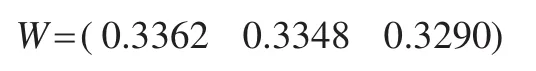
利用簡單加權(quán)對四種單一預測模型進行加權(quán)模擬，得到模擬經(jīng)營成本為：

并計算組合預測模擬經(jīng)營成本與歷史經(jīng)營成本相對誤差為：

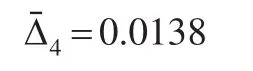
四種預測模型的模擬經(jīng)營成本與歷史經(jīng)營成本仿真對方分析圖如圖2所示。

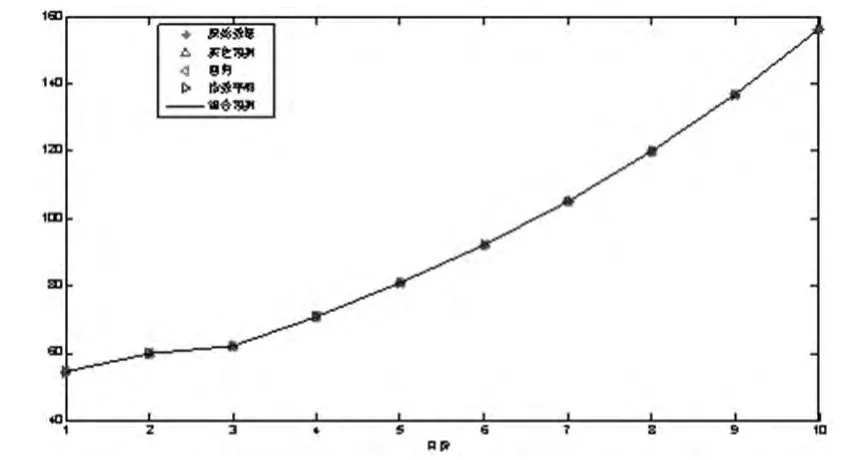
圖2 原始數(shù)據(jù)與不同預測方法模擬經(jīng)營成本對比分析圖

4 結(jié)語

成本預測是大型企業(yè)進行科學管理和企業(yè)未來生產(chǎn)經(jīng)營規(guī)劃中不可或缺的一部分，大型企業(yè)在成本預測過程中，細微的誤差都可能引起大量的資金波動，甚至導致企業(yè)資金鏈的破裂，為企業(yè)的生產(chǎn)和經(jīng)營帶來巨大的風險，所以，在成本預測過程中，選擇高精度成本預測模型是非常重要的。單一預測模型的精度已經(jīng)不足以滿足現(xiàn)有的成本預測，組合預測因為能克服單一預測方法的缺陷，已經(jīng)廣泛的被應用到成本預測過程中，研究以組合預測為主的成本預測模型應該是未來成本預測的主要趨勢。

[1]Tang X W,Zhou Z F,Shi Y.The Error Bounds of Combined Forecasting[J],Mathematical and Computer Modelling,2002,36(9).

[2]陳華友.基于相關(guān)系數(shù)的優(yōu)性組合預測模型研究[J].系統(tǒng)工程學報,2006,21(4).

[3]王應明,羅英.調(diào)和平均組合預測中的參數(shù)估計技術(shù)[J].系統(tǒng)工程與電子技術(shù),1997,19(10).

[4]殷春武,石宇翔.廣義偏差最小的組合預測加權(quán)系數(shù)確定[J].統(tǒng)計與決策，2011，(1).

[5]殷春武.加權(quán)殘差平方和最小的組合預測組合權(quán)重的確定[J].統(tǒng)計與決策，2012，(6).

[6]楊蕾，陳華友，王宇.基于貼近度的誘導廣義OWA算子最優(yōu)組合預測模型[J].統(tǒng)計與決策,2013,(5).

[7]鄧聚龍.灰理論基礎[M].武漢:華中科技大學出版社,2003.

[8]張岐山,鄧聚龍.灰關(guān)聯(lián)熵分析方法[J].系統(tǒng)工程理論與實踐,1996,16(8).