基于線性ARIMA與非線性BP神經網絡組合模型的進出口貿易預測

陳 蔚

（洛陽師范學院，河南 洛陽471022）

0 引言

進出口貿易是拉動經濟增長和實現對外交流的重要工具，多年來我國對外貿易尤其是出口貿易迅速增長，但隨著國際形勢的日益復雜化和產業競爭力的偏弱，貿易摩擦仍然十分嚴重。國家積極出臺各項產業結構調整和外貿政策，努力振興企業信心，實現對外貿易的平穩增長，根據商務部發布的報告與海關總署的統計數據，2014年前3個季度，進出口、進口、出口累計增速為7.7%、8%及7.3%，9月外貿增速僅為3.3%，較七八月份的7.8%和7.1%的增長水平大幅回落，其中出口更同比下降0.3%，上半年進出口增速波動較大，這種短期中的波動同樣體現于對外貿易的長期運行中。所以，有必要建立合理的數學模型對進出口貿易的走勢做出預測，目前采用較多的方法是基于計量經濟學的回歸預測方法和序列自回歸方法，但這些方法的缺陷在于一是難以完全搜集到影響進出口的所有因素，從而造成變量遺漏，其次只提取了線性規律而對非線性規律則無法進一步進行挖掘，所以本文擬采用ARIMA模型和BP神經網絡模型從兩個角度進行時序分析，以達到高精度預測的目的。

1 模型方法

1.1 ARIMA模型

基于時間序列的隨機特性，自回歸移動平均模型（ARIMA）能夠很好的描述變量發展規律并進行預測。對于序列yt,可以用一個自回歸過程AR(p)和一個移動平均過程MA(q）刻畫其自相關結構，記為：

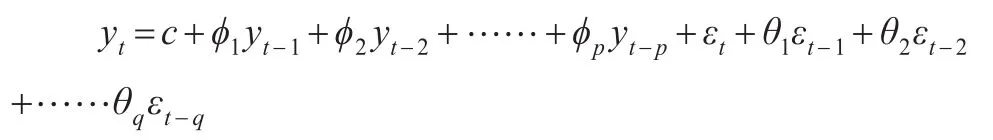
其中p，q為滯后階數，εt為白噪音序列，具有獨立同分布和服從期望為零、方差既定的正態分布。對于上式，引入滯后算子L，形成滯后多項式形式：

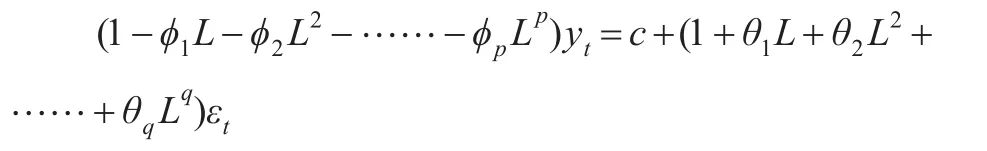
記

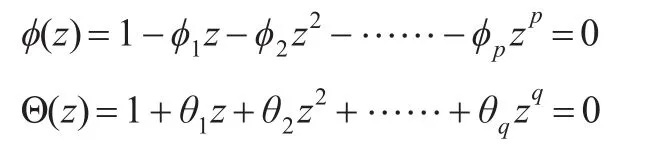
如果φ(z)特征根的倒數全部落于單位圓之內（特征根倒數模小于1），意味著滿足平穩性要求，pj(j=1，2，......m)特征根倒數有相應特征意味著滿足可逆性要求。對于平穩性序列，確定的過程依賴于相關系數圖，AR(p)的自相關AC系數呈現出正弦或指數型減弱，然后逐漸收斂于0（拖尾性），偏自相關系數PAC則在一定階數后為0,（截尾性），MA過程具有相反特征。

ARIMA模型的估計步驟為:首先進行單位根檢驗，如果非平穩則需要進行對數或差分處理形成平穩序列，其次對平穩序列建模要確定自回歸和移動平均的項數ai，根據AC和PAC判定截尾和拖尾狀態，但在實踐中，因為拖尾性和截斷性不明顯，理論界提出了不同的標準，高常水(2011)認為應當滿足三個要求：（1）估計系數全部顯著，（2）平穩性和可逆性要求，（3）隨機誤差項為白噪音。但是，樊歡歡（2009）認為ARIMA模型變量估計系數t統計量要求沒有OLS那么嚴格，只要方程擬合系數和穩定性統計量F值顯著即可。最后，進行模型估計并按照殘差最小化原則進行動態和靜態預測。

1.2 人工神經網絡BP算法

BP人工神經網絡是一種多維映射關系所得出的一種誤差自動修復機制，Rumelhart（1986）提出的該智能算法流程圖如圖1所示。

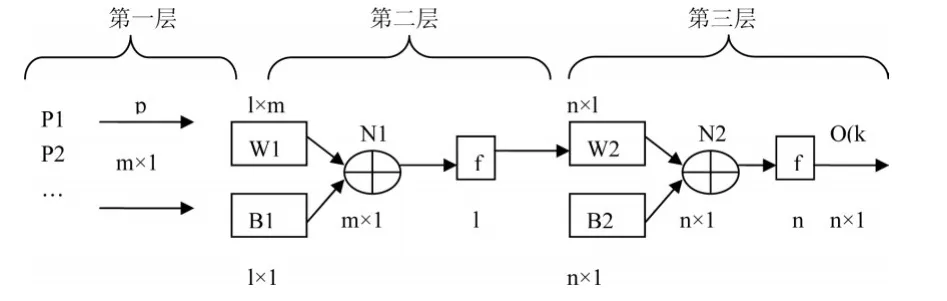
圖1 BP神經網絡

在BP網絡中，信息的遞入從輸入層開始，每一層的單個神經元與下一層中所有單元進行連接，但同層之間無聯系，下一層神經元得到的信息量實際是上層神經元信息輸入的加權平均值和本身具有的閾值之和。在輸出層，實際輸出與預期輸出間的差異形成了誤差值，利用梯度下降理論以反向態勢輸入誤差信息并對神經元間權重及閾值進行調整，以實現誤差最小化。具體過程為：

（1）第一層中節點的信息輸入為：pj(j=1，2，......m)，第二層第i節點接受信息沖擊為：

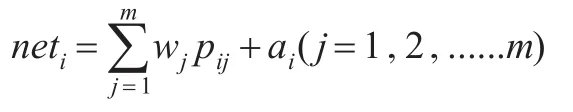
（2）ai為閾值，經過轉換函數處理后第二層i神經元輸出為：

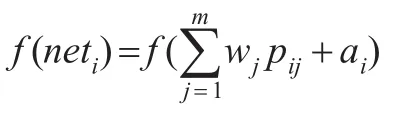
（3）第三層神經元k信息沖擊：

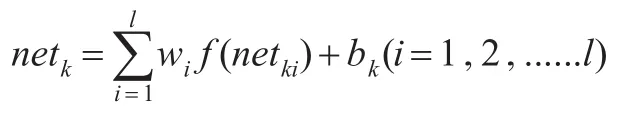
bk—j的閾值，最終網絡輸出為：

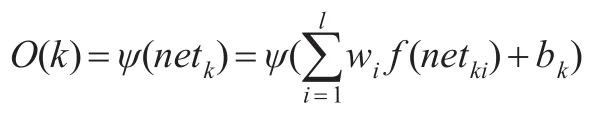
本文擬先用ARIMA模型對進出口貿易數據進行擬合，得到誤差項后進行BP網絡建模，形成非線性預測結果，最后綜合“線性+非線性”結果，與實際值進行比較并檢驗。

2 我國進出口總額的實證預測

2.1 序列的單位根檢驗

本文研究對象為1990～2013年進出口貿易總額（單位：億元），進行自回歸移動平均模型處理的前提是序列平穩，同時為了消除波動影響，對序列進行自然對數處理。對進口額（JK）和出口額（CK）求對數后得到：LnJK=log(JK),LnCK=log(CK)。單位根檢驗如表1所示。LNCK和LNJK序列的ADF單位根檢驗值為-1.795、-1.976，均大于1%、5%、10%檢驗水平的臨界值，故不能拒絕“包含單位根”的原假設。對兩個序列進行1階差分后的檢驗值分別為-4.539和-3.721，分別小于1%和5%檢驗水平下的臨界值，認為至少在5%檢驗水平拒絕“存在單位根”的原假設，即進出口額服從I（1）過程。對2階差分序列進行檢驗后發現t統計量更加顯著，伴隨概率均為0.0000。

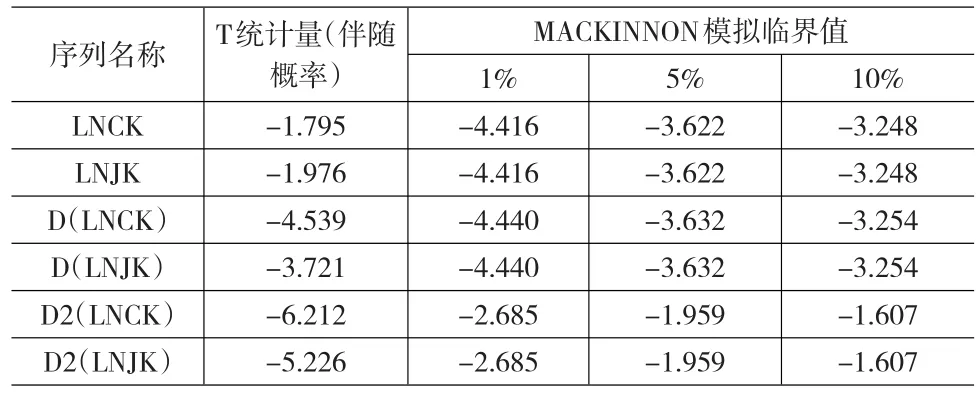
表1 單位根檢驗

2.2 ARIMA模型識別與估計

針對D2（LNCK）和D2（LNJK）序列作自相關系數圖，D2（LNCK）的偏自相關系數在1、2階超過95%的置信區間之外，其他階的PAC系數在區間之內，說明在2階截尾，自相關系數在1階超過虛線，故可對LnCK建立ARIMA(2,2,1)。D2（LNJK）的PAC系數在2階很接近虛線，其他階均在95%置信區域之內，自相關系數一直在區域之內，故本文對LnJK建立ARIMA（2,2,0）模型。

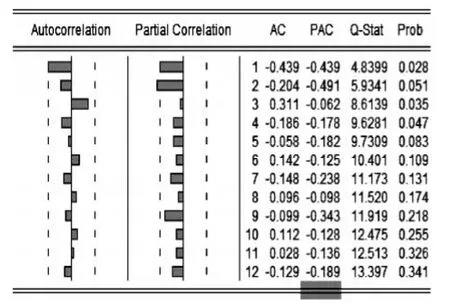
圖2 出口額2階差分序列自相關圖

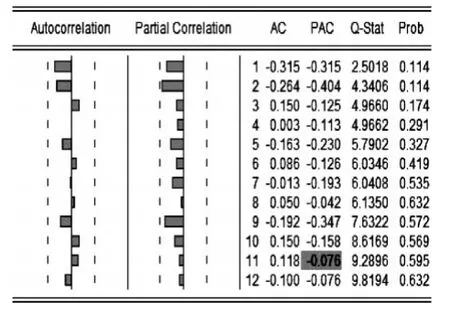
圖3 進口額2階差分序列自相關圖

以滯后算子多項式計算得到的公式(出口額）分別為：(1-0.0004φ1L+0.128φ2L2)D2(LNCK)t=-0.008+(1-0.997L)εt

計算得到的AR（p）和MA（q）的特征根的倒數分別為-0.36i，0.36i，說明模型是穩定的，MA Roots倒數為1，未處于單位圓外，故模型具有可逆性。模型的AIC和SC信息值分別為-0.454，-0.255。

得到的公式（進口額）為：

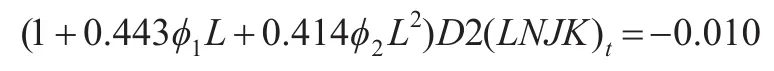
AR（P）特征根倒數為-0.22-0.060i，-0.22+0.060i，均處于單位圓之內。模型的AIC和SC信息值分別為-0.503，-0.354。

2.3 線性預測結果

表2第2、3列是用ARIMA模型估計出的我國進出口額的自然對數后二階差分項預測值，目前在EVIEWS中沒有還原選項。本文采用MATLAB7.0軟件進行還原操作，結果第4、5列。第6、7列為進口與出口的實際數據。第8、9列為預測誤差，是用實際值減去預測值得到。最后兩列為預測相對誤差，可以看出，使用ARIMA模型得到的擬合效果并不好，1995～2013年間出口與進口額的預測相對誤差分別為18.43%和47.62%。

2.4 BP神經網絡誤差預測

根據張宇青等人（2013）的做法，將采用“滾動建模法”，即使用既定區間內5年的數據作為單次輸入，然后采用區間下年（第六年）的數據作為輸出，建立輸入節點為5、輸出節點為1的BP網絡，學習樣本個數為14個。使用MATLAB7.0軟件對CKE和JKE進行BP網絡建模，第一層和第二層節點處理函數設置為雙曲正切型S函數，第三層設置為純線性函數，訓練函數采用共軛梯度方法。圖4顯示在訓練次數達到246次后，CKE建立的BP網絡訓練誤差收斂至一個很小的值，網絡建立有效。利用建立好的網絡，將2009～2013年的誤差作為輸入，得到2014年CKE為13721，然后采用2010～2014年誤差作為輸入，得到2015年誤差為7962.5，依次類推，得到2016～2018年CKE預測值，分別為23522、26336、29621，將得到的預測誤差CKF加上ARIMA模型預測的數值CKF，就得到了2014～2018年的出口貿易額數值，分別為129011.1、128938、149341.36、156035.48、162137.81。圖5為JKE序列的BP網絡訓練收斂結果，在287次迭代后誤差迅速收斂至一個較小的水平。計算出對應JKE數值，并還原預測值，得到結果如表2下方所示，2014年我國進口貿易額預測值為253867.72億元，與現實情況有悖，屬于突變點，但2015～2018年進口貿易額顯示相對合理，預計在2018年達到了192600.18億元。

3 結論

本文使用自回歸移動平均模型（ARIMA）和人工神經網絡（BP）對我國進20年來進出口貿易時間序列的線性與非線性規律進行挖掘，并對2014～2018年我國貿易狀況進行預測，結論如下：

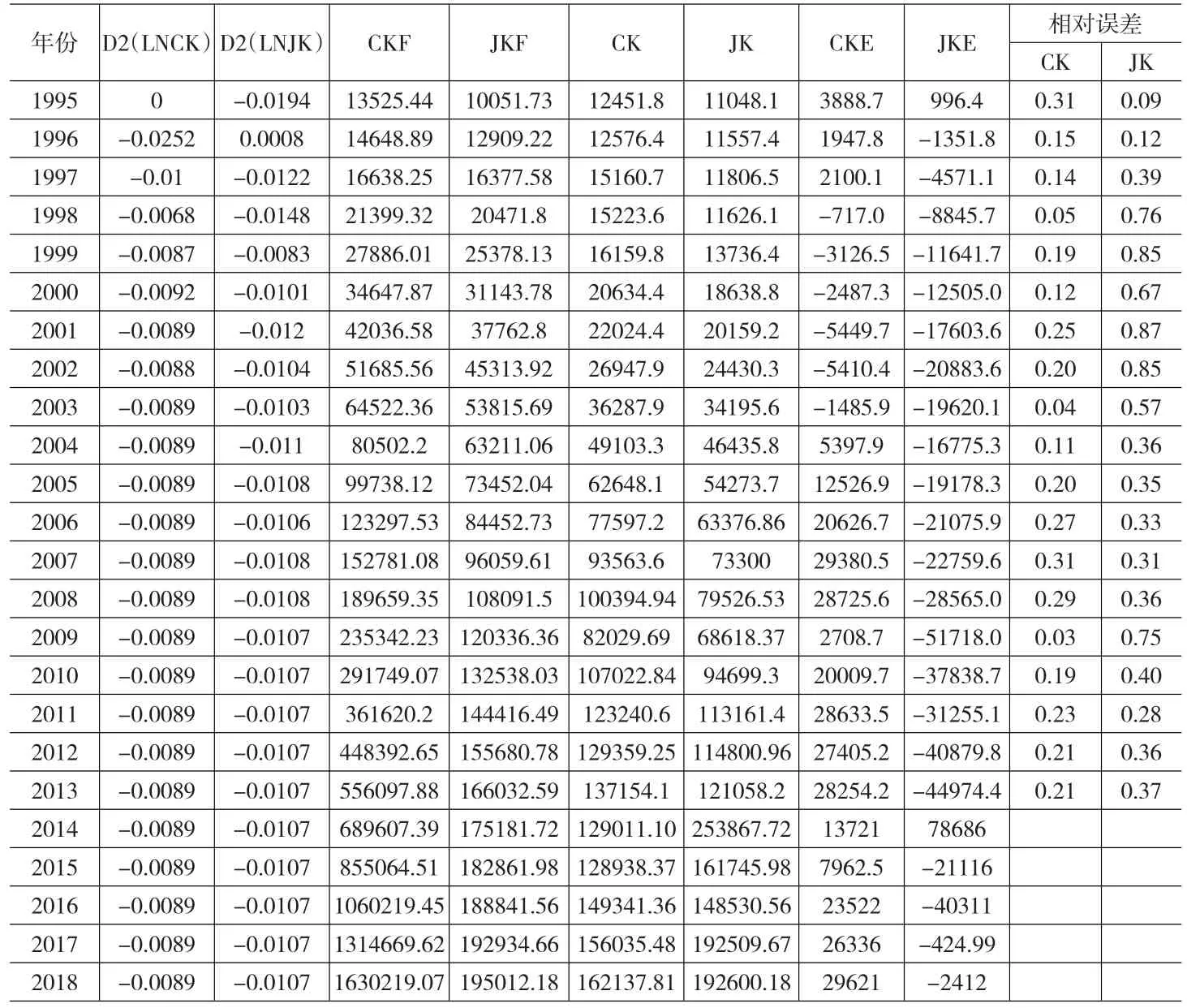
表2 我國進出口ARIMA預測結果與誤差

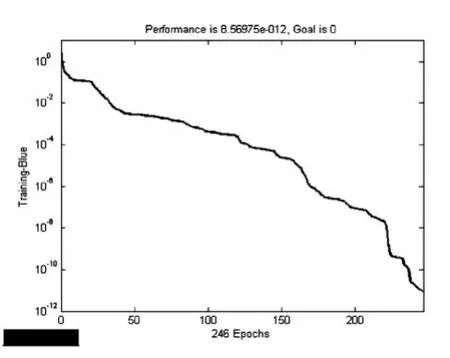
圖4 CKE網絡訓練結果

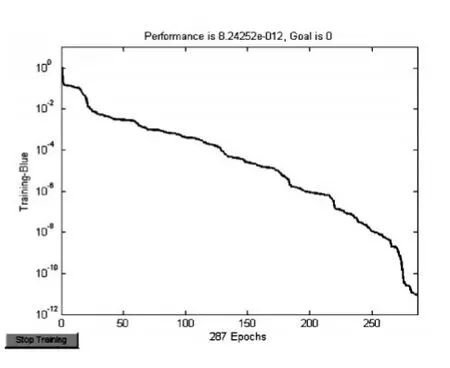
圖5 JKE網絡訓練結果

（1）ARIMA和BP神經網絡能夠分別對國際貿易額序列中的兩類規律進行挖掘，對于線性規律，可以分別用ARIMA（2,2,1）和ARIMA（2,2,0）模型對出口、進口的對數二階差分序列進行建模，從預測結果看，ARIMA模型的精度較低，預測相對誤差分別為18.43%和47.62%。使用BP方法能夠充分挖掘非線性信息，根據網絡訓練后的預測誤差能夠迅速收斂到一個很小的水平。

（2）我國多年來一直處于貿易盈余狀態，出口高于進口導致外匯儲備增加，給人民幣升值制造了壓力，也對通貨膨脹有著推波助瀾的作用，出口作為拉動經濟增長的馬車之一，為促進經濟社會發展、增強國力作出了很大的貢獻，但不可否認的是我國貿易出口總量規模龐大的背后是質量的擔憂，勞動密集型和低技術產品占總出口的比例很大，以低勞動力、原料成本為基礎的出口增長是無以為繼的。根據本文預測結果，在未來幾年出口與進口保持上漲趨勢，但從總量上進口將超過進口，造成貿易逆差。

[1]高常水，李盡法，許正中.基于ARMA模型的我國政府行政成本支出研究(1978～2009)[J].華東經濟管理，2011，（1）.

[2]樊歡歡.EViews統計分析與應用[M].北京：機械工業出版社，2009.

[3]雷可為,陳瑛.基于BP神經網絡和ARIMA組合模型的中國入境游客量預測[J].旅游學刊，2007，（4）.

[4]張宇青，易中懿，周應恒.一種線性ARIMA基礎上的非線性BP神經網絡修正組合方法在糧食產量預測中的運用[J].數學的實踐與認識，2013，（22）.