非飽水凍融作用下的古磚動彈性模量

非飽水凍融作用下的古磚動彈性模量

湯永凈1，邵振東2

(1.同濟大學 土木工程學院,教育部巖土與地下工程重點實驗室，上海 200092；

2.上海仰韶古建筑保護科技發展有限公司,上海 200092)

摘要：彈性模量是反映材料剛度的重要指標。自然界中雨淋和凍融導致古建筑砌體磚處于非飽水凍融狀態。通過大氣環境實驗艙對古磚進行非飽水凍融作用下的飽和系數、飽水度、動彈性模量、相對動彈性模量等技術參數實驗，分析了非飽水凍融作用下古磚彈性模量變化規律。實驗結果表明，飽水度大于等于60%時，非飽水凍融導致古磚試件動彈性模量和相對動彈性模量數值均出現明顯下降趨勢；飽水度小于60%時，非飽水凍融對動彈性模量和相對動彈性模量數值影響較小。非飽水凍融作用下，古磚的初始抵抗風化能力大小是影響動彈性模量和相對動彈性模量數值的重要因素。同時，對非飽水凍融作用下反映古磚抵抗凍融損傷能力的極限飽水程度等關鍵參數進行了討論。

關鍵詞：非飽和水；凍融；飽水度；動彈性模量；飽和系數

Received:2015-07-30

Foundation item：National Natural Science Foundation of China (No.52178359)

古磚孔隙自由水廣泛存在于其各種毛細孔或大孔中，自由水在毛細孔中的存在數量由材料的毛細吸水能力大小確定，決定了材料的“潮濕”程度。隨著材料毛細水的增加，毛細吸水能力逐漸減少。當材料毛細水達到飽和狀態時，毛細吸水能力為零[1]。材料的毛細吸水能力大小決定了材料飽水度大小，飽水度指材料孔隙中的充水程度。被凍固體材料在許多情況下的孔隙水是非飽和的[2]。磚石文物建筑的基礎長期處于潮濕或干濕交替環境中，導致基礎古磚孔隙水始終處于飽水及非飽水的交替轉換狀態；古建筑主體結構(例如外墻磚砌體、磚柱、屋面磚等)均在地面以上，地下毛細水作用隨建筑物高度而逐漸減弱，裸露于自然界中的古磚砌體材料和砌體結構長期被自然界中的雨水沖刷，毛細吸水能力使雨水會滲透到古磚孔隙，根據降雨量的大小和降雨時間的多少，古磚孔隙呈現不同的飽水度。一般情況下，“連續淋雨13 h以上有可能達到飽和”[2],因此，非飽水作用為古磚孔隙水的飽水常態。本文中的飽水度表示不同非飽水凍融作用下對應的古磚含水量。

飽和與非飽和的孔隙水在受凍情況下形成的損傷是不一樣的。Fagerland[3]通過對實驗數據分析提出了臨界飽和理論，認為材料都有一極限飽水程度，當實際含水量小于極限飽水程度，凍脹產生的破壞小；大于極限飽水程度時，凍脹產生的破壞大，極限飽水程度是材料抵抗凍融損傷的關鍵參數。非飽和孔隙中氣態形成的空間可以容納水變成冰后體積的改變，消除和減少了凍傷[2]。非飽水凍融是指古磚孔隙充水程度小于極限飽水程度時的凍融。

彈性模量是反應材料剛度的重要指標。彈性模量數值大小決定了古磚剛度，古磚剛度決定了磚砌體結構的截面剛度，直接影響文物建筑的變形及安全性。Powers等[4]認為凍融產生的靜水壓力是材料孔徑及孔徑分布的函數。凍融產生的靜水壓力改變了材料原有孔結構，擴大了材料內部裂紋，降低了材料致密性，削弱了古磚材料彈性模量和古磚砌體彈性模量。由于非飽水為自然界中古磚孔隙飽水常態，因此，非飽水凍融作用下古磚彈性模量變化規律的研究對磚石文物建筑的保護十分必要。

1實驗方法與實驗結果

1.1　實驗樣品信息

所有樣品磚均來自中國山西一已拆遷重建的古民居，為古民居外墻磚，外觀尺寸290 mm×140 mm×70 mm，古民居建于道光三年(公元1823年)，非文物建筑，見圖1。其所在地屬于溫帶大陸性季風氣候，年平均降水580 mm，年平均氣溫9.7 ℃，冬季歷史最低溫度-30 ℃。樣品磚數量共計80塊(含自然狀態下標準比對樣品10塊)。

圖1　古民居Fig.1　Ancient

1.2　大氣環境實驗艙

實驗驗證凍融狀態下磚的吸水能力和時間的平方根成正比[9]。隨著凍融次數的增加，材料原有孔隙體積增大并可能出現凍融裂隙，提高了材料毛細吸水能力。每5次凍融循環后的再雨淋可以起到補充磚孔隙水分的作用，淋雨量累積可以使古磚孔隙形成不同的充水程度，以達到非飽水凍融實驗中不同飽水度之目的。

圖2　大氣環境實驗艙Fig.2　Atmospheric environmental test

大氣環境艙中雨淋和凍融參數適用范圍為：溫度-40 ℃～+80 ℃；最小雨滴直徑>100 μm，最大雨滴直徑<6 400 μm；雨淋強度為0～1.7 mm/min。艙凈腔尺寸為4 000 mm×3 000 mm×3 000 mm。所有實驗參數人工設定后計算機程序自動控制記錄。

1.3　凍融實驗

參照中國砌墻磚試驗方法標準[10]，結合大氣環境實驗艙適用范圍及艙凈腔尺寸，環境艙人工設定凍融程序為：從降溫至-20 ℃開始計算凍融時間，-20 ℃凍結過程的持續時間為5 h，然后升溫到+20 ℃，升溫時間3 h，一次凍融循環結束。共計35次循環。每5次循環代表一種環境狀態，共7種環境狀態，分別用D5、D10、D15、D20、D25、D30、D35表示。升降溫度值采用試件表面溫度傳感器顯示溫度為準。

1.4　雨淋實驗

古民居所在區域年降雨量580 mm，最大雨滴直徑4.7 mm[11]，年平均氣溫9.7[12]。因此，大氣環境艙模擬雨淋參數選用雨滴最大粒徑4.7 mm。方向垂直向下，強度中擋1 mm/min，水溫10 ℃。7個不同環境狀態樣品均在對應凍融開始之前進行淋雨，每次淋雨2 h，淋雨后立即測試其飽水度。

1.5　飽和系數實驗

根據中國砌墻磚試驗方法標準[10], 把樣品置于105 ℃鼓風干燥箱烘至恒質，稱量干質量m0，然后浸泡于20 ℃淡水中24 h，稱量濕質量m24，再放入蒸煮箱中淡水沸煮5 h，稱量濕質量m5，按照式(1)計算其飽和系數值Kn。

(1)

飽和系數實驗結果見表1。

表1　飽和系數與飽水度實驗結果

1.6　飽水度實驗

飽水度S為不同淋雨狀態下的古磚飽水量與浸水24 h古磚飽水量比值，按式(2)計算。

(2)

式中:mn為不同淋雨狀態下的古磚質量；m24為浸水24 h古磚質量，m0為古磚烘至恒重的干質量。mn和m24均為古磚自由狀態下的吸水量，與自然界淋雨后的古磚吸水狀態具有可比性。

1.7　超聲法測定動彈性模量實驗

實驗采用NM-4B非金屬超聲檢測分析儀。聲波的傳播速度和測試材料的密度、剛度相關。所有試件進艙前首先烘干至恒重，分別測試其密度和初始聲時值t0,每5次凍融循環結束后，分別超聲測試該試件聲時值tn,每塊磚樣測試3點對測，見圖3。根據聲波的傳播速度υ和試件密度ρ,按式(3)計算樣品的動彈性模量Ed。

圖3　動彈性模量實驗樣品Fig.3　Elastic modulus test

(3)

式中：μ為泊松比，取0.2；ρ為磚密度；v為傳播速度；l為試樣的對測長度；t為超聲波在l長度上的傳播時間。計算相對動彈性模量Edl按式(4)計算。

(4)

彈性模量計算結果見表2。

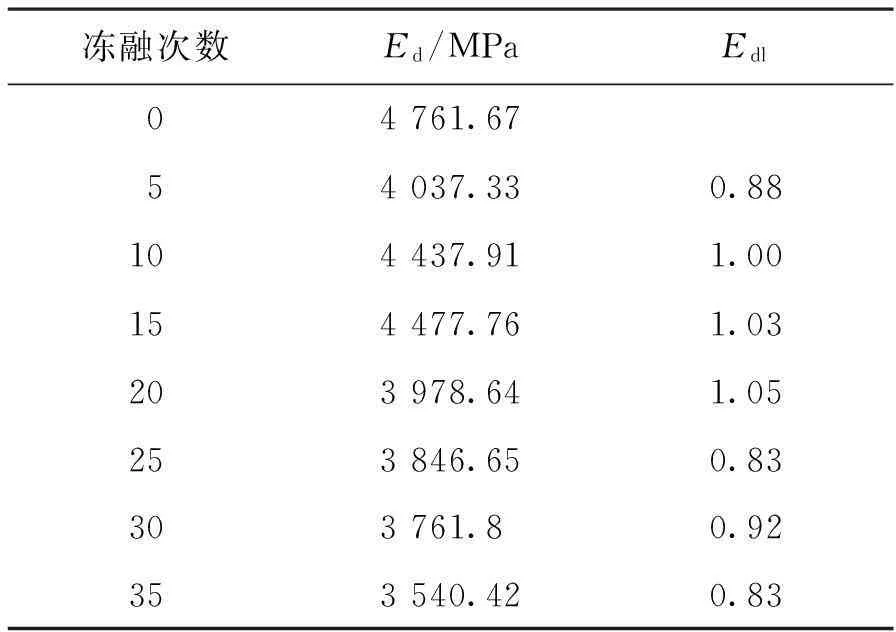
表2　動彈性模量實驗結果

2實驗結果分析

2.1　非飽和凍融狀態的彈性模量

圖4和圖5依據表2實驗結果繪制。由圖4看出，動彈性模量隨凍融次數增加呈現緩慢降低趨勢：凍融開始到20～25次凍融的初始階段，動彈性模量數值在4 000～4 500 MPa區間波動；20～25次凍融循環后，動彈性模量降低趨勢呈現規律性。相對動彈性模量的變化規律和動彈性模量變化規律基本相似：初始階段相對動彈性模量增加，20～25次凍融循環后，相對動彈性模量數值逐漸下降。宦文娟等[13]在對粘土紅磚飽和凍融實驗中也證明“相對動彈性模量隨著凍融次數的增加呈現先增加后減小的規律”，可見,Ed和Edl數值先增后減是磚的材性引起而非不同凍融形式所致。由表1可知，20～25次凍融循環對應的飽水度大約為60%。由于古磚動彈性模量和相對動彈性模量在20~25次凍融循環階段發生明顯變化。由此可知，60%飽水度是反映古磚抵抗非飽水凍融損傷能力的重要參數之一。

圖4　不同非飽和凍融次數的動彈性模量Fig.4　Dynamic elastic modulus under unsaturatedcyclic

圖5　不同非飽和凍融次數的相對動彈性模量Fig.5　Relative dynamic elastic modulus underunsaturated cyclic

古磚試件在34、35次非飽水凍融循環后呈現斷裂和塌陷。有文獻明確指出：凍傷的損害包括凍脹和局部開裂[1],因此，斷裂也是凍傷損害的結果。試驗在35次非飽水凍融對應的飽水度為77.2%。筆者建議用飽水度作為反映古磚抵抗非飽水凍融損傷能力的重要參數之一，而且該飽水度符合極限飽水度的定義。

實驗中古磚呈現開裂破壞狀態的飽水度77.2%，小于Fagerland[3]提出的極限飽水程度Scr數值91.7%。Scr數值是Fagerland通過大量混凝土實驗后提出的。因歷史氣候以及古代燒結工藝等因素影響，凍融對古磚的損傷機理是一個復雜的演變過程。如何合理確定古磚的極限飽水程度對古建筑保護有重要價值。

2.2　飽和系數與動彈性模量

依據表1和表2實驗結果繪制圖6和圖7。從圖6和圖7可以看出，古磚的動彈性模量Ed和相對動彈性模量Edl隨飽和系數大小的變化規律與圖4和圖5的結果具有相似之處：飽和系數小于0.9，Ed和Edl數值時有增加時有減少，飽和系數大于0.9以后，Ed和Edl數值呈現下降趨勢。飽和系數0.9對應的飽水度大約在50%～60%，見表2。

實驗中，35次非飽水凍融后古磚樣品即呈現斷裂和塌陷，一些粘土紅磚在65次飽水凍融后磚才呈現“片狀脫落”破壞[13]。根據靜水壓理論，65次飽水凍融對試件的損傷遠大于35次非飽水凍融。兩個實驗結果差異的原因在于采用的試件樣品磚初始狀態的抗風化能力不同。文獻[13]中粘土紅磚飽和系數凍融前為0.81、凍融后為0.86；本實驗中古磚飽和系數為凍融前0.89，凍融后0.939。根據中國砌墻磚試驗方法標準[10]中的抗風化性能評定標準，粘土紅磚在經歷了65次飽水凍融后其抵抗風化能力(0.86)仍舊好于本實驗未凍融前的古磚初始狀態(0.89)。因此，磚樣初始狀態抗風化能力的差異是實驗結果差異的原因所在。古磚因經受了200 a的自然界凍融循環影響，其抗風化能力極大削弱。在對磚進行凍融實驗研究時，其初始狀態抵抗風化的能力是非飽水凍融狀態下影響動彈性模量和相對動彈性模量的重要因素。

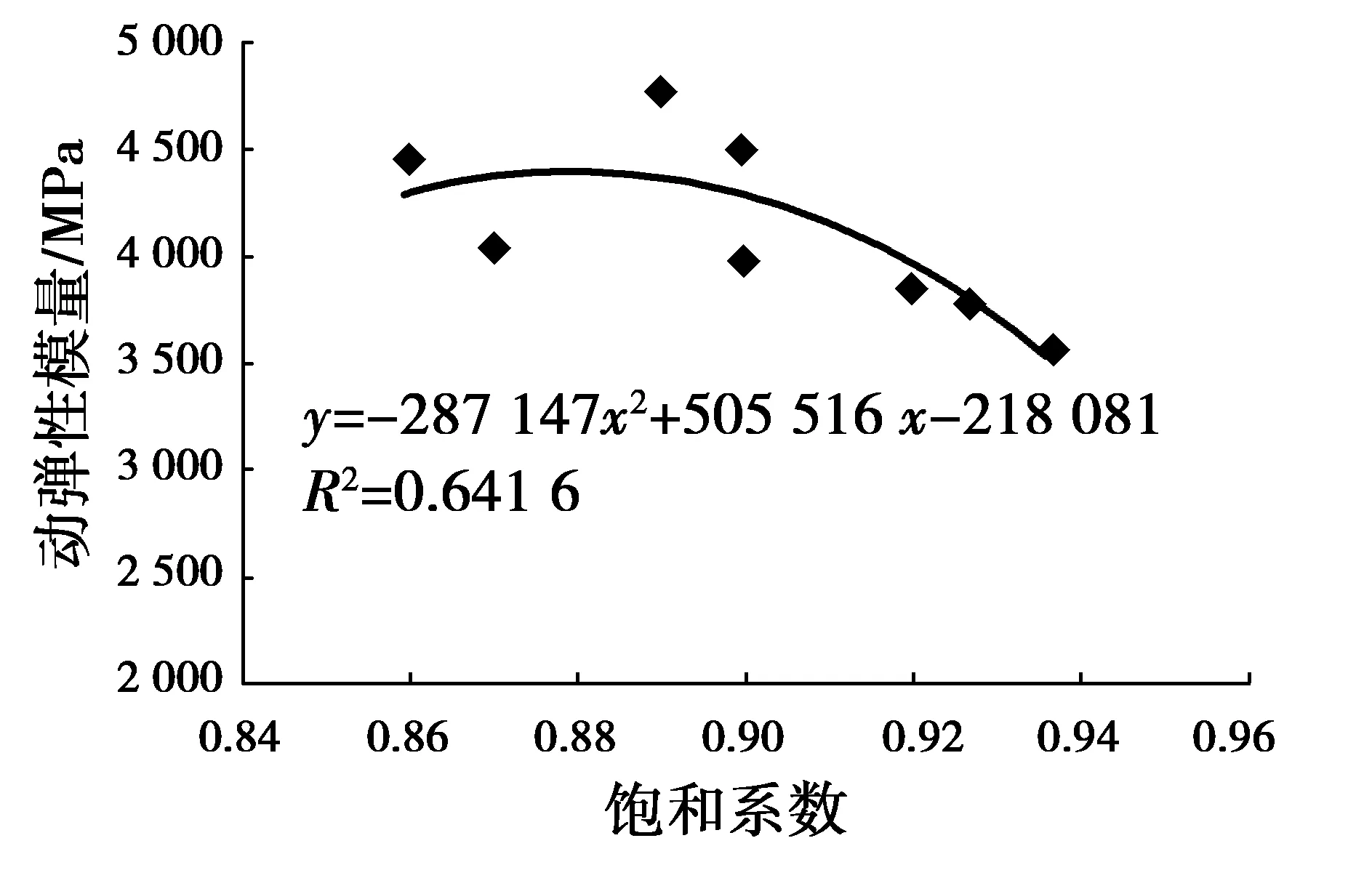
圖6　飽和系數與動彈性模量Fig.6　Saturation coefficient versus dynamic elastic

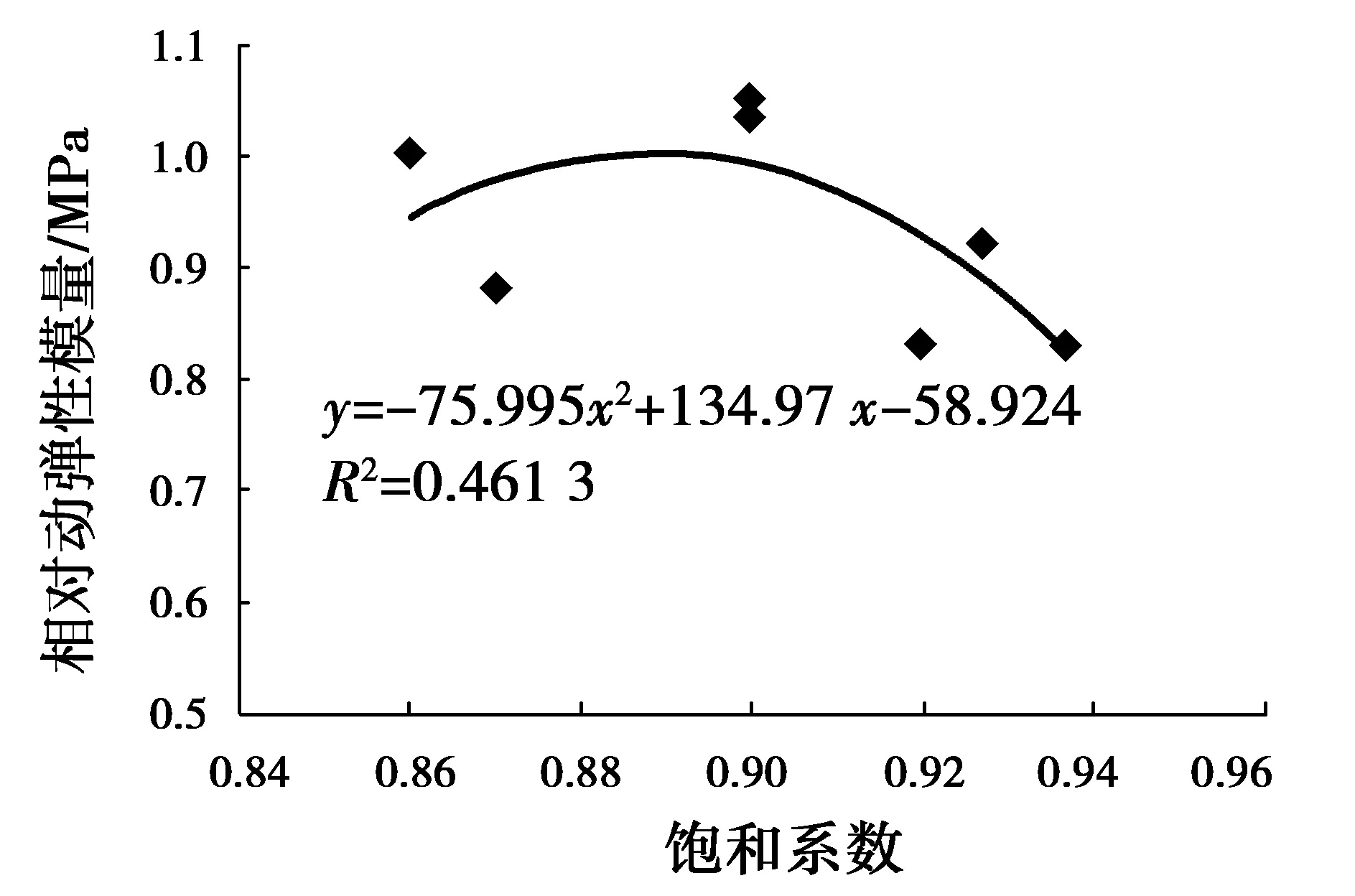
圖7　飽和系數和相對動彈性模量Fig.7　Saturation coefficient versus relative dynamic elastic

3討論

孔隙水對古磚特性影響的物理機理是一個復雜的過程，濕度梯度、表面張力和孔隙水壓力都會對古磚性能產生一定影響。從實驗結果看，當飽水度為60%時，古磚抵抗凍融損傷能力出現顯著變化，能否因此把60%飽水度確定為反映古磚抵抗凍融損傷能力的關鍵參數？當飽水度為77.2%時，古磚試件連續多次呈現斷裂。斷裂是破壞的典型特征，根據靜水壓理論，材料的凍融破壞是極限飽和狀態下的孔隙水體積膨脹的結果，能否因此判斷77.2%是實驗古磚的極限飽水程度？如何確定古磚抵抗凍融損傷能力的關鍵參數，是研究非飽水凍融作用下古磚彈性模量等材料性能的關鍵所在。然而，這些問題的正確答案并非一次實驗就能確定，而是需要大量更具代表性的專項實驗進一步驗證。筆者實驗的價值在于通過實驗發現和提出了這些問題。

需要指出的是，在飽水和非飽水凍融作用下，不同材料的動彈性模量和相對動彈性模量的變化是不一樣的。混凝土在飽水凍融后“隨著凍融次數的增加，相對動彈性模量逐漸降低”[14]。究其原因，初步認為是不同材性所致。燒結磚 “粘土顆粒之間較小的孔因燒結溫度而消失，并形成較大孔隙”[15]，而“大的孔隙對材料性能是有利的”[9]。可能這也正是一些磚砌體古建筑在千年風雨中能保存至今的原因所在。對于混凝土等其他材料在飽水和非飽水凍融作用下動彈性模量和相對動彈性模量的變化需另行研究。

4結論

1)在非飽水凍融狀態下，古磚的動彈性模量和相對動彈性模量呈現隨著凍融次數增加而降低的總體趨勢，削弱了古磚剛度。

2)飽水度≥60%時，動彈性模量和相對動彈性模量數值均出現明顯下降趨勢，反映出古磚剛度明顯削弱；飽水度<60%時，動彈性模量和相對動彈性模量數值均呈現稍有起伏但整體平穩階段，反映出古磚剛度基本穩定；當飽水度為77.2%時，古磚出現斷裂。

3)古磚初始狀態抵抗風化的能力是非飽水凍融狀態下影響古磚動彈性模量和相對動彈性模量的重要因素。

4)建議將古磚動彈性模量、相對動彈性模量以及飽水度作為古磚抗風化能力變化的評價指標。

參考文獻：

[1] Hall C, Hoff W D. Water transport in brick, stone and concrete [M].2nd ed. London: Spon Press, 2012: 45-46.

[2] Hall C, Hoff W D. Water transport in brick, stone and concrete [M].2nd ed. London: Spon Press, 2012:270-280.

[3] Fagerland G. The significance of critical degree of saturation at freezing of pore and brittle materials [C]//Proceedings of the Scholar CF, Durability of Concrete,Detroit：American Concrete Institute, 1975:13-65．

[4] Powers T C, Willis T F. The air requirement of frost resistant concrete[C]// Highway Research Board Proceedings, 1950, 29: 184-211.

[5] Krautkramer J H. Ultrasonic Testing of Materials [M]. Berlin: Springer-Verlag, 1977:26.

[6] Nagy P B. Introduction to ultra sonics, 20-251-728 [R]. Department of Aerospale Engineering and Engineering Mechanics, Ohio, USA: University of Cincinnati, 2001.

[7] Markham M F. Measurement of elastic constants by the ultrasonic pulse method [J]. British Journal of Applied Physics, 1957, 8(S6):56-63.

[8] Test method for sonic velocity in refractory materials at room temperature and its use in obtaining an approximate Young’s Modulus[S]. ASTM C 1419 Standard 1999.

[9] Hansen W, Kung J H. Pore structure and frost durability of clay bricks [J]. Materials and Structures,1988,21: 443- 447.

[10] 中華人民共和國國家質量監督檢驗檢疫總局. GB/T 2542—2012 砌墻磚試驗方法 [S].北京：中國標準出版社,2012.

General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 2542—2012 Test methods for wall bricks[S]. Beijing：China Standards Press, 2012. (in Chinese)

[11] 封秋娟,李義宇,李培仁,等.山西云微物理特征的地面觀測[J].氣候與環境研究, 2012,17(6):727-739.

Feng Q J，Li Y Y，Li P R，et al. Ground observation of microphysical properties in Shanxi Province climatic and environmental research[J]. Climatic and Environmental Research, 2012,17(6):727-739. (in Chinese)

[12] 張卉，李春華，陳永明.長治市近50年降水量變化特征及趨勢分析[C]//第31屆中國氣象學年會S8, 第16屆全國云與人工影響天氣科學會議-大氣水資源開發利用與氣象防災減災,北京,2014: 1-12.

Zhang H, Li C H, Chen Y M. The characteristics and tendency of precipitation change [C]//31thChina Meteorological Annual Symposium S8 ,16thChina cloud and Weather Science Symposium- Development and Utilization of Atmospheric Water Resources and Meteorological disaster Prevention,Beijing,2014: 1-12. (in Chinese)

[13] 宦文娟, 張云升, 劉國建,等.凍融環境下黏土紅磚的性能劣化規律與微結構演化[J]. 東南大學學報：自然科學版，2014,44(2):401-405.

Huan W J,Zhang Y S,Liu G J,et al. Performance deterioration and microstructure evolution of clay brick submitted to freeze-thaw cycles[J].Journal of Southeast University: Natural Science Edition,2014,44(2):401-405. (in Chinese)

[14] 曹大富,富立志,楊忠偉,等.凍融循環下混凝土力學性能與相對動彈性模量[J].江蘇大學學報：自然科學版，2012,34(6):721-724.

Cao D F, Fu L Z, Yang Z W, et al. Relationship between mechanical properties and relative dynamic elasticity modulus of concrete after freeze-thaw cycles [J]. Journal of Jiangsu University: Natural Science Edition, 2012, 34(6): 721-724. (in Chinese)

[15] Elert K, Cultrone G,Navarro C R,et al.Durability of bricks used in the conservation of historic buildings —in uence of composition and microstructure [J]. Journal of Cultural Heritage,2003,4(2):91-99.

(編輯胡英奎)

Author brief：Tang Yongjing (1965- ), associate professor, research interests: underground structural durability and historical building rehabilitation, (E-mail) ytang@tongji.edu.cn.

Dynamic elastic modulus based on unsaturated water freeze-thaw action for ancient bricks

Tang Yongjing1, Shao Zhendong2

(1. College of Civil Engineering;Key Laboratory of Geotechincal and Underground Engineering (Tongji University),

Ministry of Education, Tongji University, Shanghai 200092, P. R. China; 2. Shanghai YANHSHAO Protection of

Ancient Building Technology Development Co., Ltd., Shanghai 200092,P.R. China)

Abstract:Elastic modulus is one of the most important indexes to reflect material stiffness. Raining and freeze-thaw lead brick masonry to be in the state of unsaturated water freeze-thaw. The experiment aims to obtain the elastic modulus of ancient bricks under various unsaturated water freeze-thaw. The brick samples were put in the environmental chamber to carry out raining and freeze-thaw action. The experiment including saturated coefficient, saturated degree, dynamic elastic modulus and relative elastic modulus were carried out for these samples. Results show that the dynamic elastic modulus of the samples obviously decreases when saturated degree is equal to or larger than 60%; the elastic modulus of the samples have no significant change when saturated degree is less than 60%, and the samples break when their saturated degree reached a certain value. This paper also discusses parameters like limit saturated degree, which reflect the freeze-thaw resistance for ancient bricks.

Key words:unsaturated water; freeze-thaw; saturated degree;dynamic elastic modulus; saturated coefficient

作者簡介：湯永凈(1965- )，女，副教授，主要從事地下結構耐久性及歷史建筑結構修復研究，(E-mail)ytang@tongji.edu.cn。

基金項目：國家自然科學基金(52178359)

收稿日期：2015-07-30

中圖分類號：TU522.1

文獻標志碼：A

文章編號：1674-4764(2015)06-0001-06

doi:10.11835/j.issn.1674-4764.2015.06.001