變參數(shù)貝葉斯先驗(yàn)估計(jì)
李瑋軍,孟昭為
(山東理工大學(xué) 理學(xué)院,山東 淄博 255049)
變參數(shù)貝葉斯先驗(yàn)估計(jì)
李瑋軍,孟昭為
(山東理工大學(xué) 理學(xué)院,山東 淄博 255049)
研究了在非對(duì)稱損失函數(shù)下獨(dú)立隨機(jī)變量序列的變化點(diǎn)的貝葉斯先驗(yàn)估計(jì),以及在平方損失函數(shù)下變化點(diǎn)的貝葉斯先驗(yàn)估計(jì)和二者的比較,最終使在平方損失函數(shù)下得到的參數(shù)值較小。
貝葉斯估計(jì);貝葉斯先驗(yàn)估計(jì);非對(duì)稱損失函數(shù);變化點(diǎn)
1 問題背景
現(xiàn)有的數(shù)理統(tǒng)計(jì)分為經(jīng)典學(xué)派和貝葉斯學(xué)派。貝葉斯統(tǒng)計(jì)與經(jīng)典統(tǒng)計(jì)學(xué)的差別在于是否使用先驗(yàn)信息。貝葉斯估計(jì)不僅在統(tǒng)計(jì)學(xué)中占據(jù)著重要地位,在金融經(jīng)濟(jì)等其他領(lǐng)域也有著廣泛的應(yīng)用。貝葉斯先驗(yàn)估計(jì)是根據(jù)已有數(shù)據(jù)去估計(jì)未知參數(shù)的某些性質(zhì)的方法。
20世紀(jì)50年代, Robbins在文獻(xiàn)[1]中最早提出經(jīng)驗(yàn)貝葉斯估計(jì)的概念,此方法把經(jīng)典的統(tǒng)計(jì)方法和貝葉斯方法結(jié)合在一起,從此開啟了統(tǒng)計(jì)學(xué)中一扇新的大門。近幾十年來,國內(nèi)外許多學(xué)者對(duì)經(jīng)驗(yàn)貝葉斯做了很多研究和探索,不僅得到了豐富的理論成果,還得到了很多經(jīng)驗(yàn)貝葉斯實(shí)際應(yīng)用范例。文獻(xiàn)[2]研究了連續(xù)性單參數(shù)指數(shù)族中參數(shù)的經(jīng)驗(yàn)貝葉斯估計(jì)問題;文獻(xiàn)[3]研究了離散型單參數(shù)指數(shù)族參數(shù)經(jīng)驗(yàn)貝葉斯估計(jì)的漸近最優(yōu)化問題;文獻(xiàn)[4]研究了多元線性回歸模型的經(jīng)驗(yàn)貝葉斯估計(jì)問題;文獻(xiàn)[5]研究了線性指數(shù)模型參數(shù)的經(jīng)驗(yàn)貝葉斯估計(jì)問題。
然而在現(xiàn)實(shí)生活中,許多理論或者模型都考慮了統(tǒng)計(jì)模型的結(jié)構(gòu)變化,從而忽略了在實(shí)際觀測(cè)中的不穩(wěn)定序列可能會(huì)使很多重要數(shù)據(jù)丟失的情況,這可能會(huì)導(dǎo)致錯(cuò)誤的結(jié)果。
2 變化點(diǎn)的貝葉斯先驗(yàn)估計(jì)
假設(shè)X1,X2,…,Xm,Xm+1,…,Xn是一個(gè)至多一個(gè)變化點(diǎn)的隨機(jī)變量序列,當(dāng)
(1)
變化點(diǎn)m是一個(gè)未知的離散隨機(jī)參數(shù)。然后假設(shè)尺度參數(shù)θ1和θ2,并且每個(gè)m都是先驗(yàn)獨(dú)立的。
對(duì)于一個(gè)變化點(diǎn),讓p0表示零假設(shè)H0:m=n的后驗(yàn)概率,那么(1-p0)就是備擇假設(shè)H1:m≠n的后驗(yàn)概率。
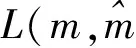
(3)
其中變量u決定損失函數(shù)的形狀。
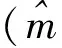
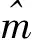
(4)
假設(shè)期望存在,那么K01就是滿足H0的后驗(yàn)概率。
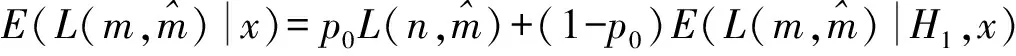
則
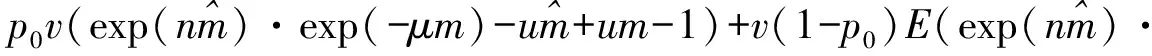
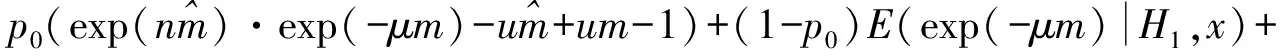
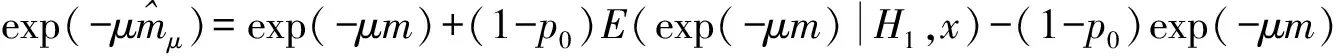
兩邊取對(duì)數(shù)得:
等式右邊提出exp(-μn)可得
定理1得證。
推論1 在形式上變化點(diǎn)的貝葉斯先驗(yàn)估計(jì)反映了在備擇假設(shè)H1:m=1,2,…,n-1形式下變化點(diǎn)的可能替代值的不確定性。
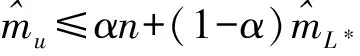
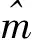
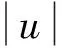
當(dāng)K01>0,0 本文得到了在LINEX損失函數(shù)下獨(dú)立隨機(jī)變量序列的變化點(diǎn)的貝葉斯先驗(yàn)估計(jì)。值得注意的是,在LINEX損失函數(shù)下p=0的貝葉斯先驗(yàn)估計(jì)和在平方損失函數(shù)下得到的參數(shù)值比在LINEX損失函數(shù)下得到的要小。 [1] ROBBINS H.An Epirical Bayes approach to statistic[M]//Third Berkeley Symposium on Mathematical Statistics and Probability.Berkeley:University of California Press,1955:157-163. [2] SINGH R S.Empirical Bayes estimation in lebesgue exponential families with the rates near the best possible rate[J].Ann Statist,1979(7):890-902. [3] CHEN X R.Asymptotically optimal empirical Bayes estimation for para-Meter of one-dimention discrete exponential families[J].Ann Math,1983(4):41-50. [4] SINGH R S.Empirical Bayes estimation in a multiple linear regression model[J].Ann Inst Stat Math,1985,37:71-86. [5] GELFAND B P,SMITH A F M.Hierarchical Bayesian Analysis of Change point Problems[J].Applied Statistics,1992,41(2):389-405. [6] LU D K,BOSE S.A Bayesian Approach to Loss Robustness[J].Statistical Decisions,1998,16:65-87. [7] MICHEAS A C.Ranges of Posterior Expected Losses and Epsilon-Robust Actions[C]//Robust Bayesian analysis,Lecture notes monograph series.New York:Springer-Verlag,2000:145-160. [8] 劉次華.線性指數(shù)模型參數(shù)的經(jīng)驗(yàn)貝葉斯估計(jì)[J].華中科技大學(xué)學(xué)報(bào),2006(3):111-114. [9] 薛嬌,常勝,鄧麗.定時(shí)截尾樣本下兩參數(shù)指數(shù)-威布爾分布的可靠性Bayes估計(jì)[J].重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)版),2014(8):132-139. [10]何朝兵,劉華文.IIRCT下幾何分布參數(shù)多變點(diǎn)的貝葉斯估計(jì)[J].西南師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2014(1):1-6. [11]朱宗元,穆良平,史代敏.基于動(dòng)態(tài)線性模型的中國狹義貨幣需求及缺口的貝葉斯估計(jì)[J].數(shù)理統(tǒng)計(jì)與管理,2013(2):268-277. [12]齊華,王恒,劉軍.可變周期的基于貝葉斯估計(jì)的TPSN改進(jìn)算法[J].傳感技術(shù)學(xué)報(bào),2013(3):407-410. (責(zé)任編輯 何杰玲) Variable Parameters Bayesian Prior Estimate LI Wei-jun, MENG Zhao-wei (School of Science, Shandong University of Technology, Zibo 255049, China) This paper studied the estimation of Bayesian prior sequence of independent random variables under asymmetric loss function point, under squared loss function changes of Bayesian prior estimate and the comparison of the two. Eventually we got that under squared loss function, the parameter value is the smallest. Bayesian estimation; Bayesian prior estimate; asymmetric loss function; change point 2015-09-29 基金項(xiàng)目:山東省自然科學(xué)基金資助項(xiàng)目(ZR2013FM012) 作者簡介:李瑋軍(1989—),男,山東淄博人,碩士研究生,主要從事應(yīng)用統(tǒng)計(jì)研究。 李瑋軍,孟昭為.變參數(shù)貝葉斯先驗(yàn)估計(jì)[J].重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)版),2015(12):143-146. format:LI Wei-jun, MENG Zhao-wei.Variable Parameters Bayesian Prior Estimate[J].Journal of Chongqing University of Technology(Natural Science),2015(12):143-146. 10.3969/j.issn.1674-8425(z).2015.12.024 O211 A 1674-8425(2015)12-0143-043 結(jié)束語

