不同磨耗階段貨車車輪與固定轍叉的接觸分析

馬 賀，李 霞，張 軍

(1.大連交通大學 機械工程學院，遼寧 大連 116028;2.大連交通大學 交通運輸工程學院，遼寧 大連116028;3.北京建筑大學 機電與車輛工程學院，北京 100044)*

0 前言

道岔是列車實現轉線運行的必備設備，在鐵路軌道中占有重要地位，而轍叉是道岔的重要組成部分，其按構造類型可分為固定轍叉與可動心軌轍叉，由于可動心軌轍叉不適應重載鐵路大軸重、高密度、大運量的運輸模式，除在必要地段鋪設可動心軌轍叉之外，其余均鋪設固定轍叉，因此固定轍叉在重載運輸中占絕大多數.

目前廣泛應用的固定式轍叉直接影響道岔的容許通過速度，又是道岔使用壽命最短的部件.固定轍叉破損多發生在從咽喉到心軌頂寬50 mm區段的心軌和翼軌部件(占84%)，傷損情況如圖1所示，圖中為現場拍攝的心軌傷損情況，具體位置為距離理論尖端360～480 mm之間.

圖1 固定轍叉心軌剝離掉塊現象

針對重載鐵路固定轍叉磨耗嚴重問題國內外專家與學者不僅從道岔線型［1］、鑄造工藝［2］、轍叉材料［3］以及考慮對轍叉進行打磨［4］等方面進行研究從而延長其使用壽命，并且應用有限元與動力學對固定轍叉進行了大量的研究.陳嶸、王平等人通過建立三維有限元模型，在疲勞荷載與極限荷載作用下對75 kg/m鋼軌12號固定轍叉薄弱部位進行強度檢算，并提出改進建議［5-6］.重載線路小范圍內試用嵌入式組合高錳鋼轍叉，董彥錄根據實體有限元方法，運用ANSYS建立三維實體計算模型，計算分析嵌入式組合高錳鋼轍叉的受力性能，提出在所選的薄弱位置鋼軌件(翼軌和心軌)均滿足強度要求［7］.

當車輛通過道岔時，輪軌接觸應力位置不斷變化［8］，道岔的幾何外形對于輪岔的動力學影響較大，而車輪型面對其影響較小［9］.運行方向對道岔上最大橫向接觸力的影響較大，而對垂向接觸力的影響小，線路對垂向接觸力的影響顯著;提高列車速度導致列車在通過道岔時接觸力變大［10-11］.上述專家與學者的研究均是以標準的車輪型面為基礎，但是實際運用中的車輪型面很快磨耗成為非標準的型面，因此研究不同磨耗階段車輪型面與轍叉的接觸分析尤為重要.

1 數據采集與型面分析

隨著列車的不斷運行，車輪產生磨耗現象，車輪型面隨之變化，當車輪磨耗到一定程度要對其進行鏇修，在車輪一個鏇修周期內應用車輪型面測量儀對大秦線C80貨車進行跟蹤測試，得到上百條車輪型面，統計分析選出如圖2所示具有代表性的車輪型面，標準LM型為鐵標規定的貨車所用型面，Ⅱ、Ⅲ、Ⅳ、Ⅴ型為磨耗到不同程度的車輪型面.

從圖2中可以看出，貨車車輪輪緣較踏面部位磨耗嚴重，輪緣均勻磨耗，踏面前期磨耗嚴重后期磨耗量較小，磨耗Ⅱ、Ⅲ、Ⅳ型為磨耗中期型面，其線型基本保持不變.固定轍叉包括翼軌與心軌，現場調研表明更換轍叉的原因多為心軌剝離掉塊嚴重.

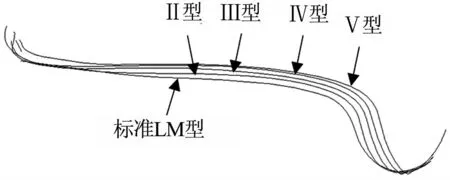
圖2 五種不同磨耗階段車輪型面

由于固定轍叉心軌距離理論尖端在360～480 mm之間磨耗嚴重，因此應用上述車輪型面與75 kg/m鋼軌12號道岔固定轍叉距離理論尖端360與480 mm這兩個截面建立彈塑性接觸模型，并對其進行計算，分析不同磨耗階段車輪與轍叉的接觸情況，兩位置處的轍叉型面如圖3所示.

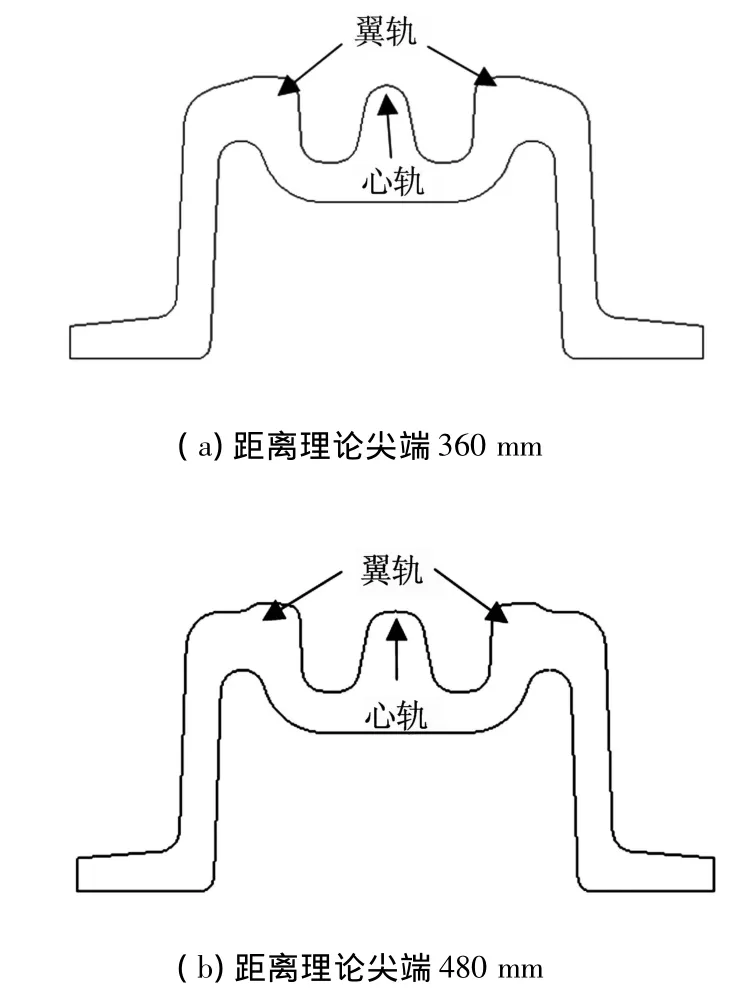
圖3 轍叉型面

在距離理論尖端360與480 mm兩個位置處車輪與固定轍叉可能產生的接觸位置為踏面外部與翼軌接觸、踏面中部與心軌接觸兩部分，不同輪叉之間的接觸位置與接觸狀態不同，需對其進行具體分析.

2 彈塑性有限元模型的建立

應用上述五種不同磨耗階段貨車車輪與距離理論尖端360與480 mm位置處的標準轍叉型面建立輪叉彈塑性接觸有限元模型，其本構關系采用雙線性模型，材料的屈服極限為689.6 MPa，楊氏模量為 2.05 GPa.

車輪與轍叉之間的約束與載荷施加情況如圖4所示，轍叉底部全約束，限制轍叉的剛體位移;車輪兩端約束橫向與縱向位移;半軸重125 kN垂直施加在軸箱所在車軸位置處.

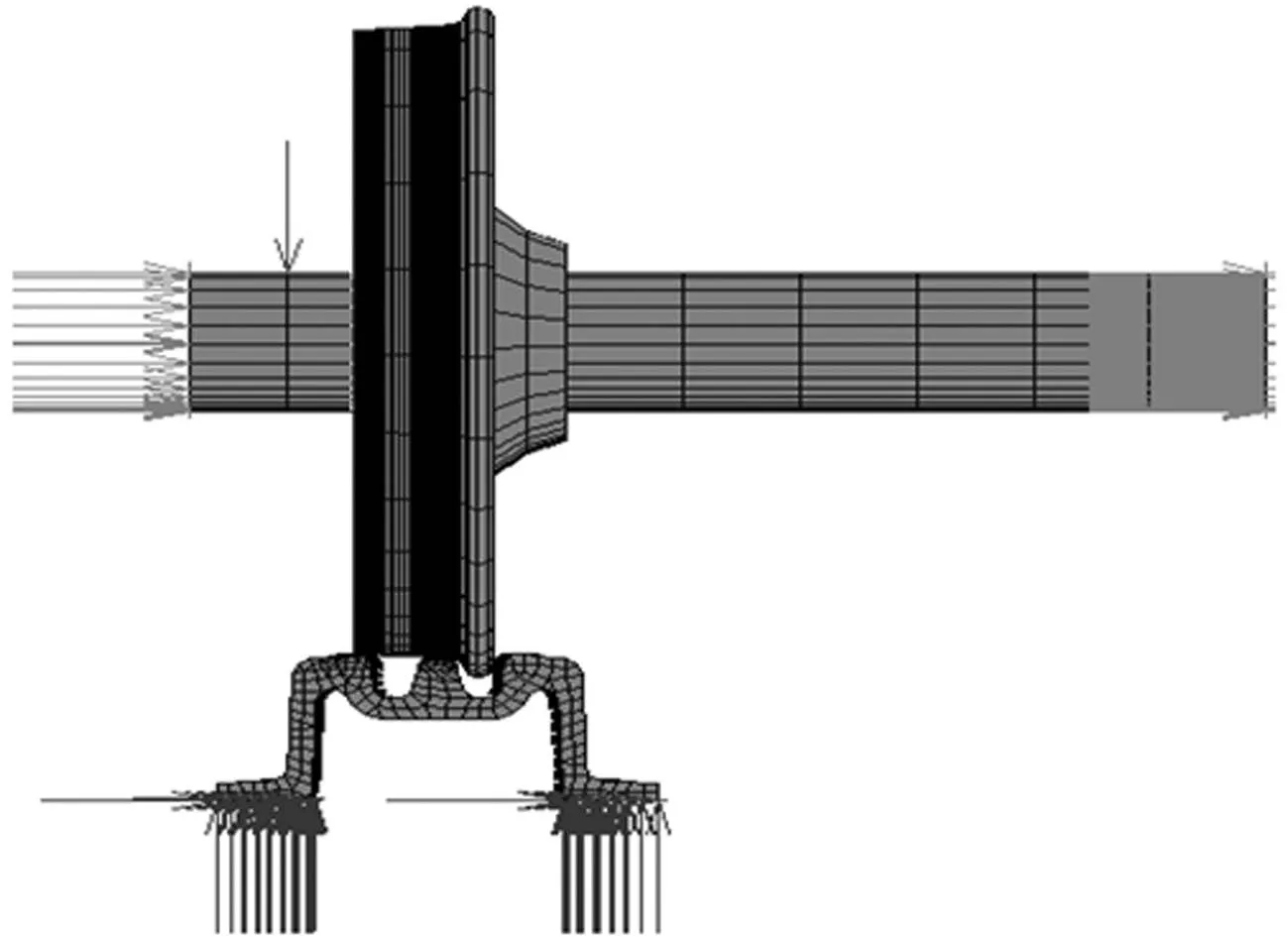
圖4 約束與載荷

3 計算結果分析

固定轍叉包括翼軌與心軌兩部分，從其結構來看，車輛逆向通過固定轍叉的過程必然是先與翼軌接觸，最后完全過渡到心軌上，過渡過程一定包括單點接觸與兩點接觸，不同車輪通過轍叉的位置不同，對轍叉產生不同的影響.通過對不同磨耗階段車輪與固定轍叉兩截面的彈塑性接觸計算，分析其接觸斑與等效應力情況.

3.1 接觸斑分析

不同磨耗階段車輪與固定轍叉兩位置處截面接觸時心軌接觸斑與翼軌接觸斑形狀均呈近似矩形，如圖5所示，其接觸斑長度范圍為21～28 mm，寬度范圍為2～5 mm，接觸斑狹長，接觸面積小.

圖5 接觸斑形狀

將不同磨耗階段車輪與固定轍叉距離理論尖端360與480 mm位置處的接觸斑位置統計如表1所示.

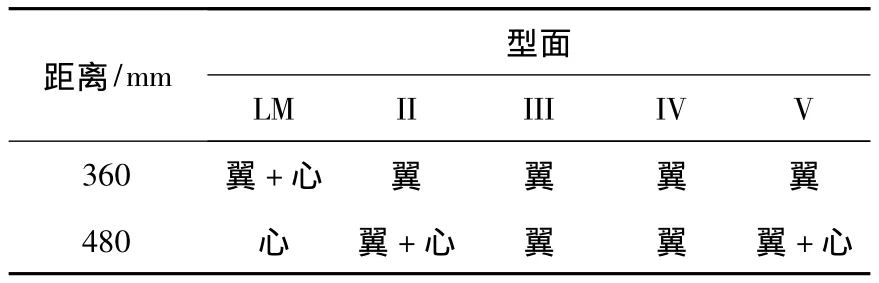
表1 不同接觸狀況下的接觸斑位置

標準75 kg/m鋼軌12號道岔固定轍叉的結構特點是翼軌逐漸降低，心軌逐漸上升.從表1中可以看出，標準LM車輪在距離理論尖端360 mm處時與翼軌和心軌同時接觸，說明此時車輪正在從翼軌向心軌過渡，在距離理論尖端480 mm處完全過渡到心軌上;磨耗III型與磨耗IV型車輪在距離理論尖端480 mm位置處還只與翼軌接觸，其通過固定轍叉時的過渡位置在距離理論尖端480 mm以后;而磨耗II型與磨耗V型車輪在距離理論尖端360 mm處時還只與翼軌接觸，在480 mm處與翼軌和心軌同時接觸，說明車輪通過轍叉的過渡位置位于480 mm之前，即此兩種車輪型面在距離理論尖端360～480 mm之間開始與心軌接觸，逐漸過渡到心軌上，車輪與翼軌和心軌同時接觸的接觸斑如圖6所示.心軌接觸斑位于心軌中心線附近，而翼軌接觸斑位于翼軌邊緣.

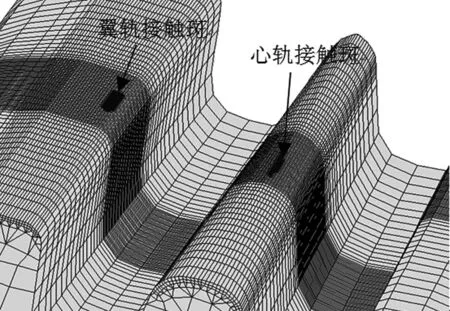
圖6 翼軌與心軌接觸斑

3.2 等效應力分析

針對輪叉的彈塑性接觸計算所得的等效應力為Von Mises應力，其作為衡量應力水平的主要指標，是正應力與剪切應力的組合，常用來描述復雜應力狀態.圖7為車輪與轍叉翼軌和心軌同時接觸時的內部等效應力圖，從圖中可以看出，其最大等效應力為1 296 MPa，超過了材料的屈服極限，位于距離輪叉表面2～3 mm之間.

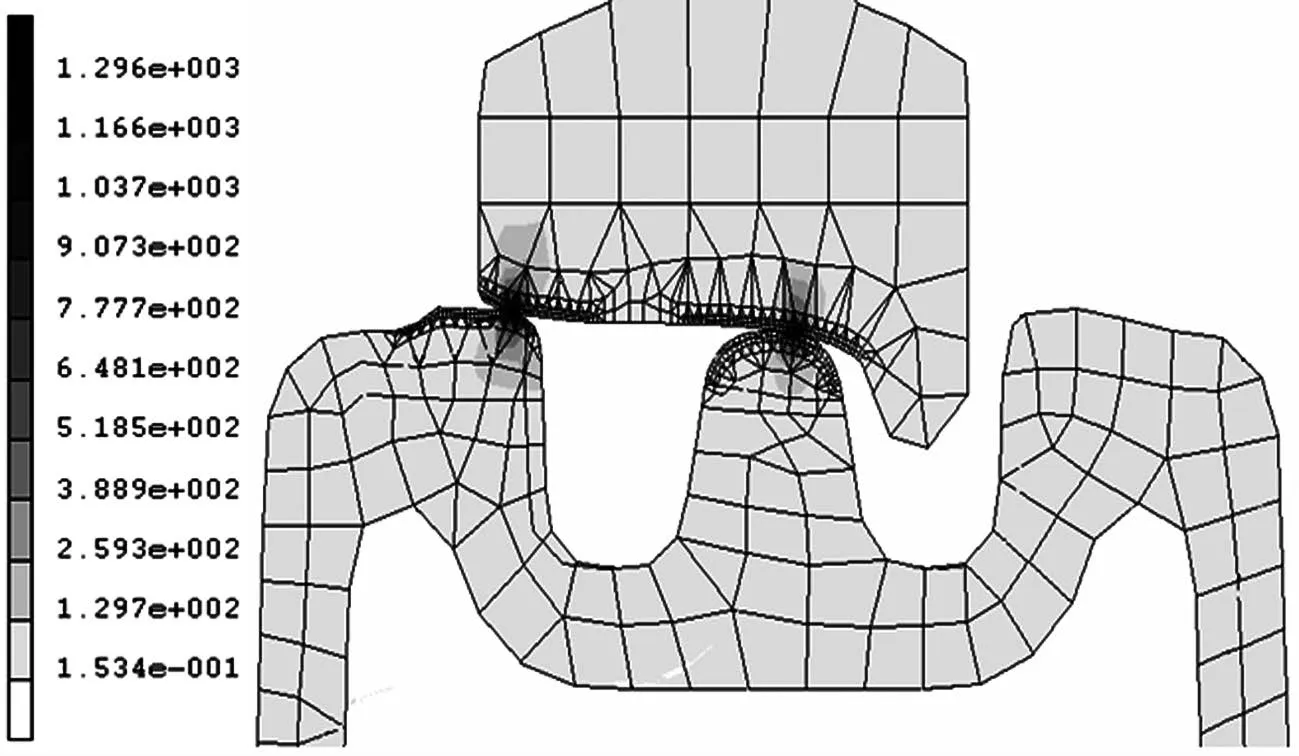
圖7 輪叉內部等效應力

圖8為不同車輪型面與固定轍叉距離理論尖端360與480 mm之間的最大等效應力.從圖中可以看出，隨著車輪的磨耗，車輪與轍叉之間的最大等效應力逐漸增大，標準車輪與標準轍叉之間的等效應力最小，輪叉匹配情況良好.由于車輪與轍叉之間的接觸面積小，其等效應力均超過了材料的屈服極限，車輪與轍叉均進入塑性變形階段.

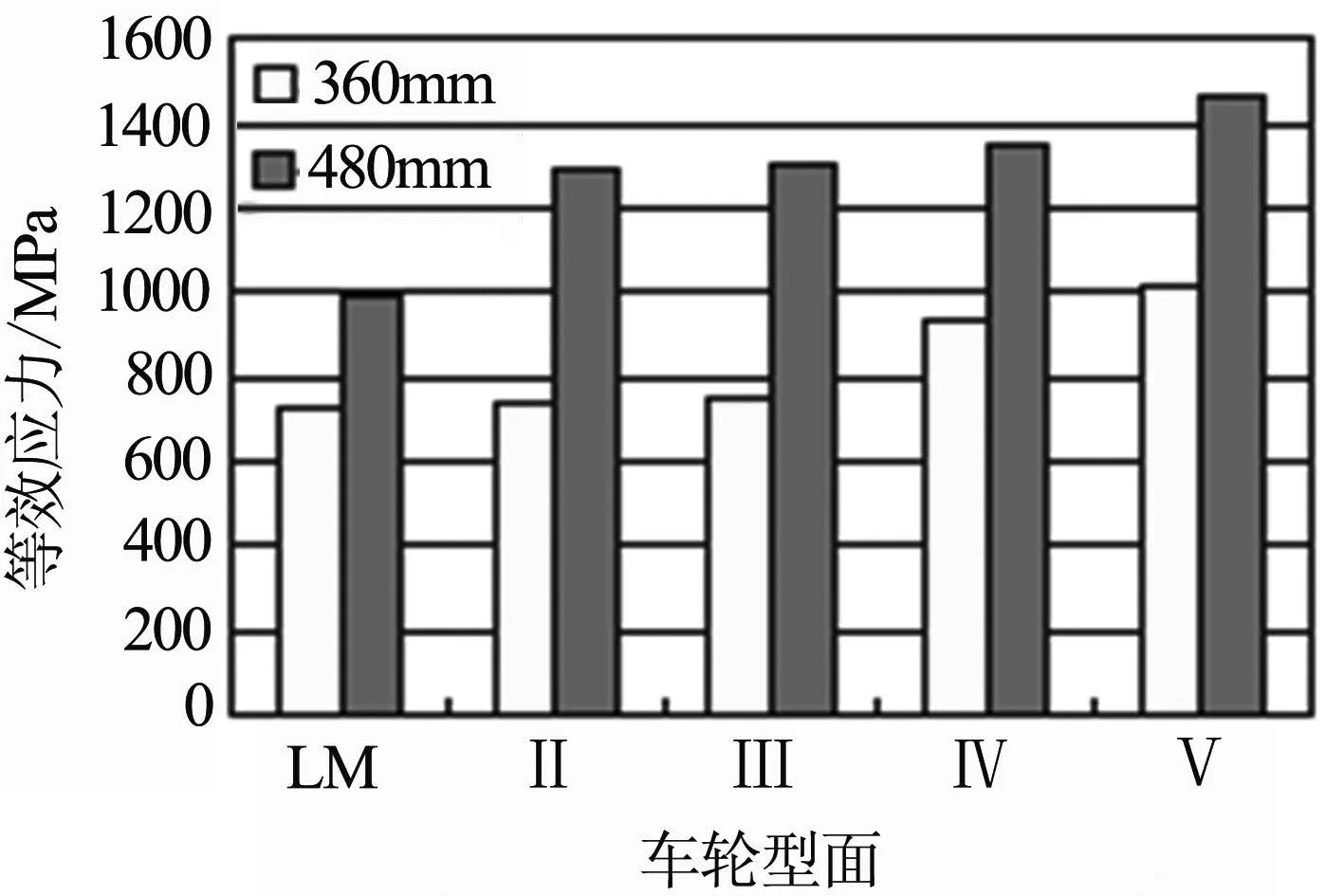
圖8 不同車輪型面與轍叉之間的等效應力

當同一車輪分別與距離理論尖端360與480mm位置的固定轍叉接觸時其最大等效應力在480 mm位置處比在360 mm位置處高出36.2% ～74.5%，這也是此位置處嚴重傷損的原因之一.

4 結論

通過對不同磨耗階段車輪與固定轍叉距離理論尖端360與480 mm兩位置處的彈塑性接觸計算分析，得到以下結論:

(1)不同車輪通過固定轍叉的過渡位置不同，對心軌與翼軌產生的影響有所差異;

(2)輪叉之間的等效應力均超過了材料的屈服極限，車輪與轍叉進入塑性變形階段.在距離理論尖端480 mm位置處的輪叉等效應力遠大于360 mm位置處的等效應力，這也是心軌此位置處磨耗嚴重的原因之一;

(3)標準車輪與標準轍叉之間的等效應力最小，輪叉匹配情況良好.隨著車輪的磨耗，輪叉之間的等效應力逐漸增大.

由于車輪通過固定轍叉是一個動態的過程，同時固定轍叉存在軌線不連續問題，車輪與轍叉心軌接觸的瞬間會對心軌產生沖擊，因此不同車輪與轍叉之間的作用情況還需進行動力學分析.

［1］王建軍.組合轍叉合金鋼心軌加工工藝［J］.鐵道技術監督，2011(10):47-50.

［2］高紅星.高效率轍叉加工技術及其設備的研究設計［D］.蘭州:蘭州理工大學，2011.

［3］張紹彤.伊朗高錳鋼轍叉的結構研究［J］.唐山學院學報，2009(3):14-16.

［4］張福成，呂博，鄭春雷，等.高錳鋼和貝氏體鋼轍叉失效機理及其磨面組織［J］.機械工程學報，2008(12):232-237.

［5］陳嶸，王平，陳小平.75kg/m鋼軌12號高錳鋼轍叉受力有限元分析［J］.路基工程，2009(4):26-28.

［6］郭利康，王平，陳小平.大秦線75kg/m鋼軌12號高錳鋼固定轍叉受力分析［J］.鐵道建筑，2009(6):114-117.

［7］董彥錄.重載鐵路道岔研究［J］.中國鐵路，2013(6):12-15.

［8］EUSTON T，ZAREMBSKI A，HARTSOUGH C，et al.Analysis of wheel-rail contact stresses through a turnout［C］.2012 Joint Rail Conference，2012:1-8.

［9］RODRIGO F L，ASIER A，JORDI V，et al.Rail vehicle passing through a turnout analysis of different turnout designs and wheel profiles［J］.Journal of Rail and Rapid Transit，2012，226(6):587-602.

［10］NIELSEN J K E.Dynamic interaction between train and railway turnout:full-scale field test and validation of simulation models［J］.Wagon System Dynamics，2008(46):521-534.

［11］ANDERSSON T D.Wheel rail impacts at a railway turnout crossing［J］.Journal of Rail and Rapid Transit，1998，212(2):123-134.