可變點約束疊前流體因子直接提取方法

楊培杰， 王長江， 畢俊鳳， 劉書會

1 中石化勝利油田分公司勘探開發研究院， 東營 257015 2 中石化勝利油田分公司博士后工作站， 東營 257015

?

可變點約束疊前流體因子直接提取方法

楊培杰1,2， 王長江1， 畢俊鳳1， 劉書會1

1 中石化勝利油田分公司勘探開發研究院， 東營 257015 2 中石化勝利油田分公司博士后工作站， 東營 257015

以Gassmann流體因子(Gassmann Fluid Item, GFI)為目標，提出了一種流體因子直接提取的新方法.首先，以貝葉斯反演框架為基礎，將似然函數、先驗信息以及Gassmann流體因子近似方程相結合，得到初始的目標函數；其次，進一步在初始目標函數中加入可變數量的點約束信息，并得到最終的目標函數；最后，通過求解該目標函數，就直接提取出了Gassmann流體因子.該方法的主要特點是不需要初始模型的參與，而是通過一個約束模型來控制提取結果的穩定性和準確性，并且可以從約束模型中選定不同數量的約束點進行約束，稱為可變點約束.給出并討論了三種常用的不同點約束模式和原則，并用模型說明了它們不同的約束效果.模型驗證和實際應用結果皆以表明，該方法即使在疊前數據信噪比很低的情況下也能較好地提取出Gassmann流體因子，流體因子提取結果客觀性高、穩定性好，并且能夠與已知的流體解釋結果很好地匹配，益于進一步推廣應用.

流體因子； 疊前反演； 可變點約束； 直接提取； 客觀性； 穩定性

1 引言

目前，流體因子在儲層流體識別中具有非常重要的意義(Smith and Gildow, 2000; Quakenbush et al., 2006; 印興耀等, 2013a)，而疊前地震反演是流體識別最有效的手段.傳統的作法是首先反演縱波速度、橫波速度和密度三個數據，然后用這三個數據間接地計算λρ、μρ、Russell流體因子等流體信息，這種作法的不足之處是會帶來累計誤差.針對這一問題，很多學者開展了基于疊前反演的流體因子直接提取方法(宗兆云等, 2012; 印興耀等, 2013b)，其優勢在于能夠減小累計誤差，因此結果更加準確可靠.

在疊前反演方面，前人已經做過很多相應的研究.基于波動方程的疊前反演(Mora, 1987; Shi et al., 2007)，在理論上比較成熟，但由于其正演模擬過程的復雜性和計算花費大，在實際中并沒有廣泛應用.基于Zoeppritz近似方程的疊前AVO反演(Hampson, 1991;Simmons and Backus, 1996; Buland and Omre, 2003)是目前發展最為迅速、深入，也是靈活性和效果最好的疊前反演方法.彈性波阻抗反演(Connolly, 1999; Whitcombe, 2002; 王保麗等, 2005)簡潔高效，是目前工業上應用最廣泛的疊前反演方法，但是由于該方法使用的是部分疊加的角道集數據，損失了一部分的疊前AVO信息，因此反演結果的準確性方面不如疊前AVO反演.

在疊前流體識別方面，Smith和Gidlow(1987)等提出用加權疊加方法得到縱橫波速度相對變化量，并從反演結果估算流體因子和檢測氣層的方法.Fatti等(1994)用權疊加的方法得到了縱波阻抗的相對變化量和橫波阻抗的相對變化量.Goodway等(1997)通過反演得到λρ和μρ等數據體，用于描述儲層的巖性和含流體性質，要比用縱波阻抗和橫波阻抗更直觀.Gray(2002)改進了Goodway方法，從疊前數據中反演出了λ和μ，消去了密度的影響，可以更好地描述巖性和流體.Russell等(2003)在前任研究的基礎上，得到了流體飽和條件下的流體因子，稱為Russell流體因子，并通過疊前反演的方法間接的獲得了該流體因子.在國內方面，也有很多專家學者進行了疊前流體因子提取方面的研究(寧忠華等, 2006; 鄭靜靜等, 2011; 宗兆云等, 2012; 印興耀等, 2013b)，并取得了較好的應用效果.

本文是在前人(Russell et al., 2003; Downton, 2005; 宗兆云等, 2012)和筆者自己所做研究(Yin and Yang, 2008; 楊培杰和印興耀, 2008)的基礎上，提出了一種直接提取Gassmann流體因子的新方法.以貝葉斯反演框架為基礎，并加入可變數量的點約束信息來穩定提取結果，來構造目標函數，最終實現了Gassmann流體因子的直接提取.該算法的核心是通過可變數量的點來約束提取的過程，可以使用兩個點，也可以使用多個點進行約束，可以使用較精確的約束模型進行約束，也可以使用極低頻約束模型進行約束，因此約束過程靈活，同時，該方法不需要初始模型的參與，由于沒有初始模型的影響，因此該方法的提取結果更加客觀準確.

模型試算表明，該方法對于地震數據中的噪聲不敏感，即使在信噪比很低的情況下也能較好地提取流體因子.實際應用表明，流體因子提取結果分辨率高、穩定性好，對于不同流體的區分效果較好，并且與已知的流體解釋結果能夠很好地匹配，同時，該方法既可以使用疊前角道集，又可以使用疊前共成像點道集，適用范圍較廣，益于進一步推廣應用.

2 貝葉斯反演框架

將地球物理信息轉化為儲層信息屬于反演的問題，從概率統計的角度，任何的反演問題可以看成是一種貝葉斯估計問題(Ulrych et al., 2001; Tarantola, 2005)，即，通過觀測數據不斷地更新先驗知識，從而得到問題的解，公式為

(1)

其中，m是待估計(反演)的參數空間，c是歸一化的常數，σpost(m)是后驗概率密度函數，pprior(m)是先驗概率密度函數，pdata[d-f(m)]是似然函數，d是觀測數據，f(m)表示正演算子.在本方法中m表示Gassmann流體因子.

對于式(1)的求解方法一般有兩種(Bosch et al., 2010)，第一種是通過最優化目標函數(Yang et al., 2008)來求解，屬于確定性反演方法；第二種是通過隨機模擬(Haas and Dubrule, 1994)的方法來實現，稱為隨機反演方法.本文采用第一種求解的思路，其優點是計算速度快、多解性小.

3 方法原理

3.1 Gassmann流體因子近似方程

Russell等人基于Biot-Gassmann理論對飽含流體多孔介質的AVO理論進行了研究，并推導了包含Gassmann流體因子的反射系數近似公式(Russell et al., 2011)，公式為

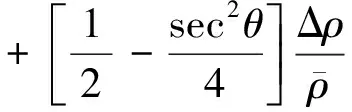
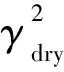
(3)

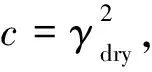
Gassmann流體因子可直接作為流體因子來識別儲層流體類型，目前已有學者對不同流體因子的敏感性進行了定量的分析(Chi and Chi, 2006; 張世鑫, 2012)，認為Gassmann流體因子對于不同流體的識別最為敏感，無論是對氣、油、水的區分度最高.式(2)和式(3)即為Gassmann流體因子直接提取的理論基礎.需要指出的是，通過式(2)可提取出三個不同的參數，即Gassmann流體因子、剪切模量和密度，本文只考慮Gassmann流體因子的提取.

3.2 初始目標函數的建立

將公式(2)按偏移距寫成矩陣形式為

(4)

其中，θ1,θ2,…,θK表示分界面處的平均入射角度，Rf、Rμ、Rρ分別表示Gassmann流體因子反射系數、剪切模量反射系數和密度反射系數.

將上式擴展為

(5)

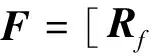
文獻(Downton, 2005; 楊培杰, 2008)指出，由于待反演的三個參數之間一般是統計相關的，因此需要應用三者之間的協方差矩陣對參數進行去相關處理，目的是提高解的穩定性，經過處理后的待反演參數之間是相互獨立的.

公式(5)進一步變成：

(6)

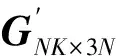
假定地震數據的噪聲服從正態分布，且獨立，F服從柯西分布(楊培杰, 2008)，用公式(1)將似然函數、先驗分布以及正演公式結合起來，就得到了初步的目標函數為

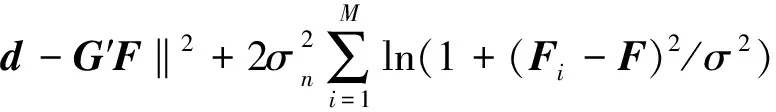
3.3 可變點約束目標函數的建立

如果對式(7)的目標函數直接進行求解，由于該目標函數中沒有考慮模型的約束作用，所以會導致反演結果的穩定性不好，特別是三維的反演結果，橫向上的連續性會很差，因此，我們提出了一種新的約束思路，通過在提取過程中加入可變數量的點約束來達到穩定反演結果、提高反演結果的客觀性、準確性的目的，公式推導過程如下.

在反射系數較小時有：

(8)

其中，rg為Gassmann流體因子反射系數.上式相對于時間積分，可以得到相對流體因子為

(9)

其中，Fg(t0)為初始流體因子的數值.將上式簡記為

(10)

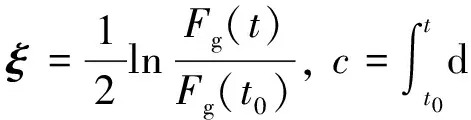
進一步地將式(10)進行擴展，就可以得到可變點約束的矩陣方程為

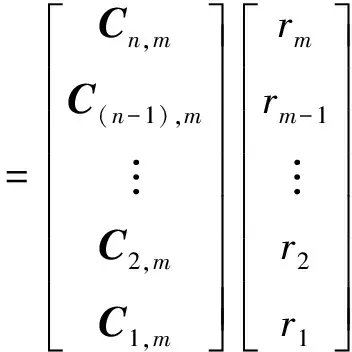
(11)

其中，n是約束點的數量，是變化的，m≥n>1，m是待反演的地震道的總點數，C是1行m列的向量.將點約束矩陣方程簡記為

(12)

那么根據貝葉斯公式，定義新的目標函數為minJ(F)=JG(F)+JP(F)+Jf(Fg)=JG(F)+JP(F) +α(C×Fg-ξ)T(C×Fg-ξ)，

(13)

當點約束的矩陣中的n選不同的值時，就可以實現待反演數據不同數量和不同時間點處的點約束.

式(13)即為最終的目標函數，下面將目標函數的每一項對參數求導，并令導數為零，最終可以得到式(14)的矩陣方程組為

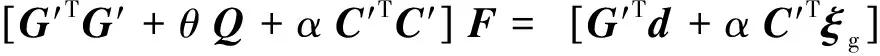
(14)

4 模型試算與分析

4.1 一維流體替代模型

首先構造砂泥巖互層模型(圖1)，然后基于Gassman理論，分別用氣、油、水對砂巖進行流體替代，并計算砂巖含氣、含油和含水后的縱波速度、橫波速度和密度，如圖2所示，其中，氣砂孔隙度30%，含氣20%；油砂孔隙度30%，含油90%；水砂孔隙度30%，含水90%.

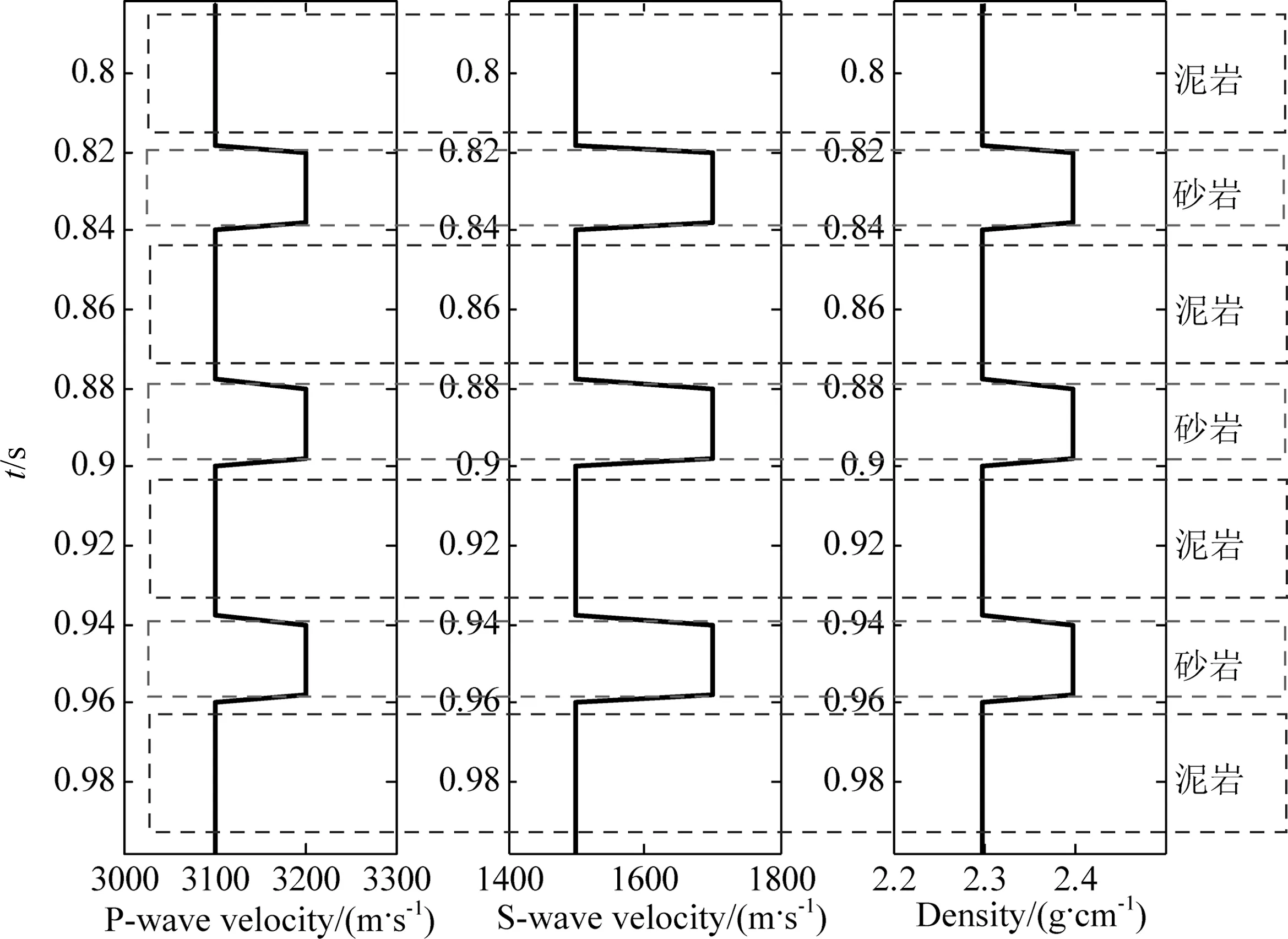
圖1 砂泥巖薄互層模型Fig.1 Thin sand-shale interbed model

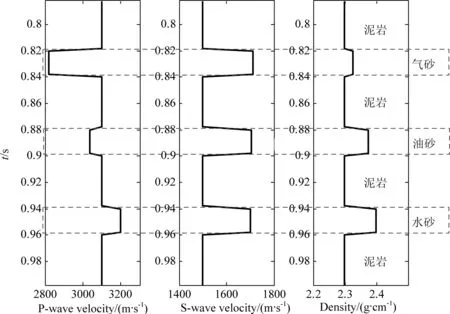
圖2 流體替代后砂泥巖薄互層模型Fig.2 Thin sand-shale interbed model after fluid substitution

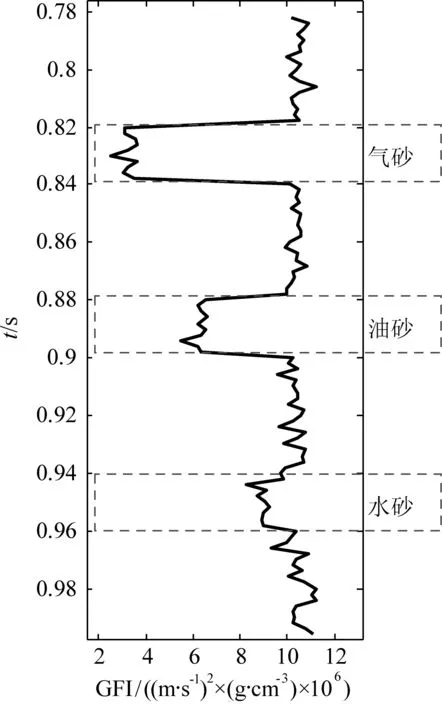
圖3 模型的Gassmann流體因子Fig.3 Gassmann fluid factor of the model

用公式(3)計算流體替代后模型的Gassmann流體因子，如圖3所示，該模型數據被加入了一定的噪聲，目的是使之更接近真實的地層參數.

以圖2中的縱橫波速度、密度為輸入，應用30 Hz的混合相位子波，進行基于Zoeppritz方程的疊前地震正演，為了說明本文提出的方法優秀的抗噪性，在道集中加入信噪比2∶1的隨機噪聲，如圖4所示.

圖5為沒有可變點約束的流體因子直接提取結果，由于疊前合成記錄的信噪比很低，并且沒有模型的約束，提取結果的穩定性和分辨率都比較差，雖然氣層有較好的提取結果，但是對于油層，特別是水層的結果不理想.

4.2 可變點約束模式

下面以該流體替代后的模型為例，來說明點約束的三種不同模式及其應用效果.

約束模式1：約束點的數量n=2，此時，認為待反演地震道的第一個點和最后一個點的流體因子值是已知的，其他所有的點都是未知的.α的取值應大一些，一般100>α>50.此時的可變點約束的矩陣方程如式(15)所示，其點約束的效果如圖6所示，公式(15)為

(15)

約束模式2：m>n>2，m是待反演地震道的總點數，該模式一般是在模式1的基礎上，再根據工區的實際情況選擇若干個點，此時α的取值應小一些，一般50>α>1.假設約束點數量n=5，此時的可變點約束的矩陣方程如式(16)所示，其點約束的效果如圖7所示，公式(16)為

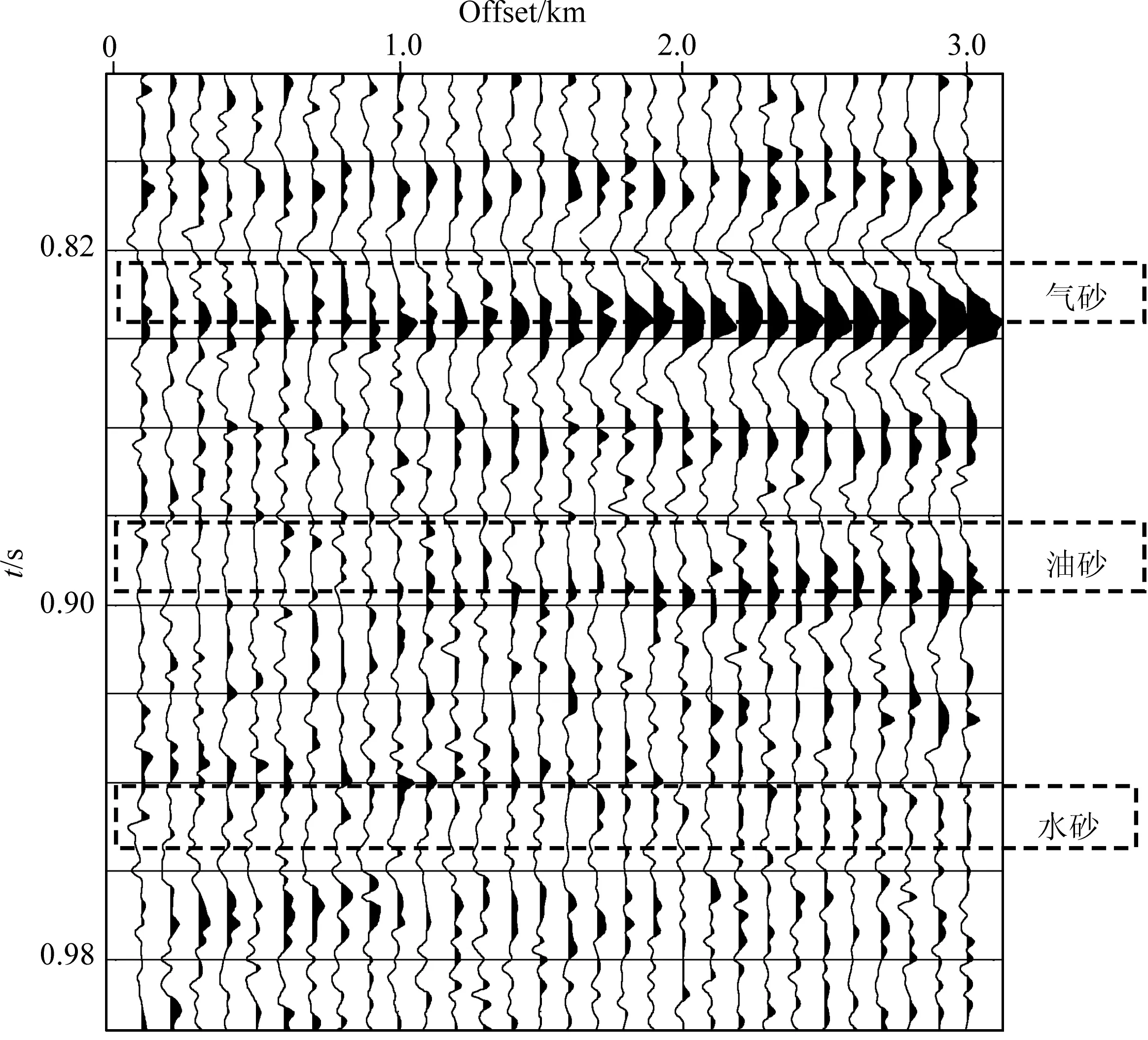
圖4 疊前合成記錄(S/N=2)Fig.4 Prestack synthetic record (S/N=2)

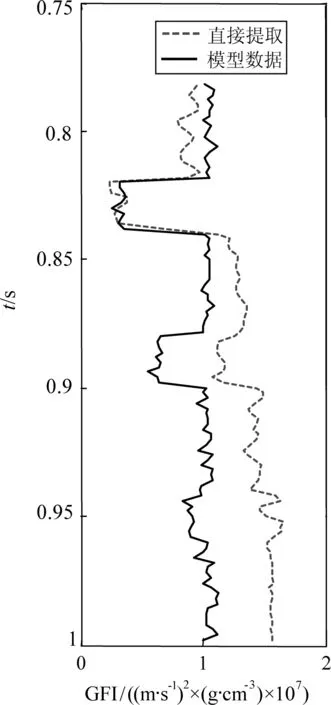
圖5 無約束提取結果(S/N=2)Fig.5 Unconstrained extraction results (S/N=2)

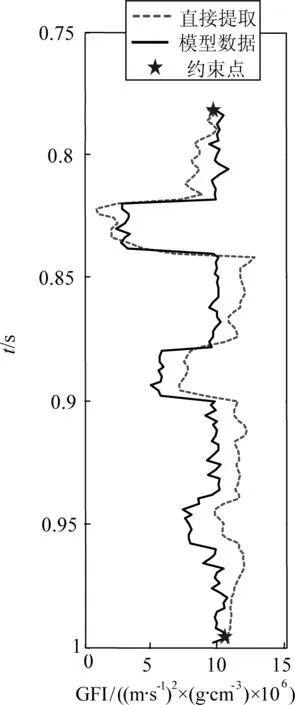
圖6 模式1提取結果(S/N=2)Fig.6 Extraction result with pattern 1

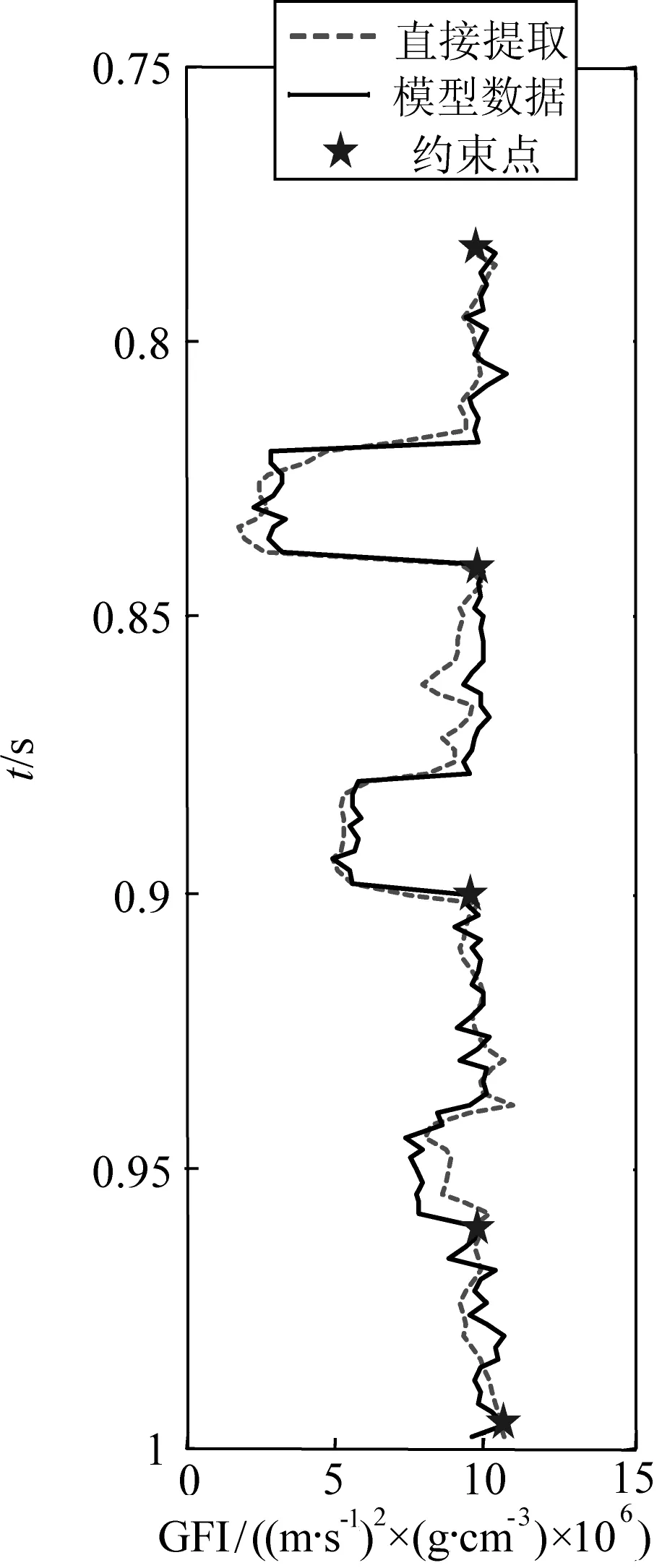
圖7 模式2提取結果(S/N=2)Fig.7 Extraction result with pattern 2

(16)

約束模式3：n=m，即使用和待反演的地震道相同的點數來進行約束，這時不使用高頻的初始模型，而是往往使用一個極低頻的模型(極端情況下是使用一個常數模型進行約束)，此時α的取值應最小，一般1>α，則反演結果不會和約束模型很像，而是往模型靠攏，即能夠起到穩定反演結果的目的.此時的可變點約束的矩陣方程如式(17)所示，其點約束的效果如圖8所示，公式(17)為

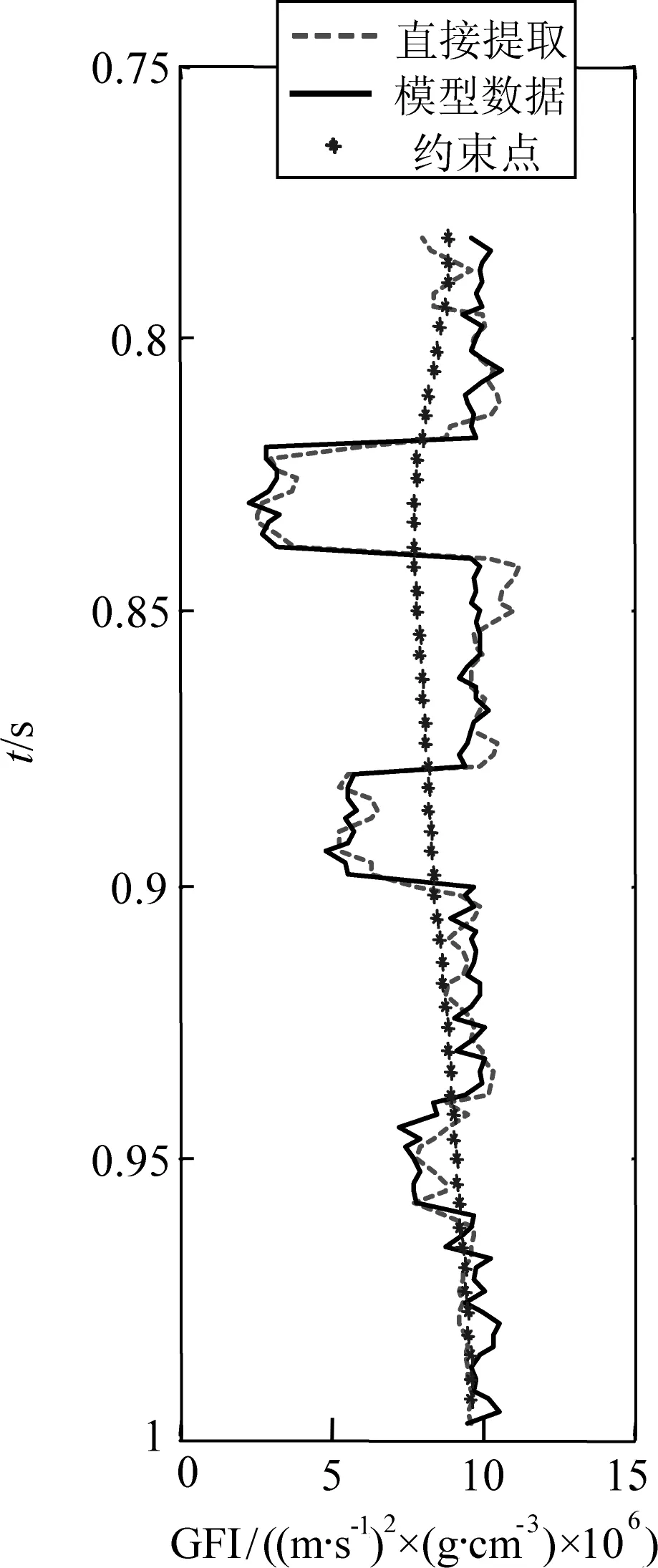
圖8 模式3提取結果(S/N=2)Fig.8 Extraction result with pattern 3

(17)

為了便于理解和應用，對不同的可變點約束模式與原則進行了總結，如表1所示.

4.3 二維模型分析

下面用一個二維Gassmann流體因子模型來說明不同約束模式的適用條件和應用效果，如圖9所示，并設置一口虛擬井Well A，用于提供約束模型.圖10是首先根據二維Gassmann模型的縱波速度、橫波速度、密度進行疊前正演，得到疊前道集后，再對疊前道集進行疊加的剖面，在該剖面上解釋了5個層位，用來提供約束點信息，從深到淺分別是h0、h1、h2、h3、h4.此次模型反演使用的是三個角度的角道集數據，信噪比為4∶1.

表1 約束模式與原則

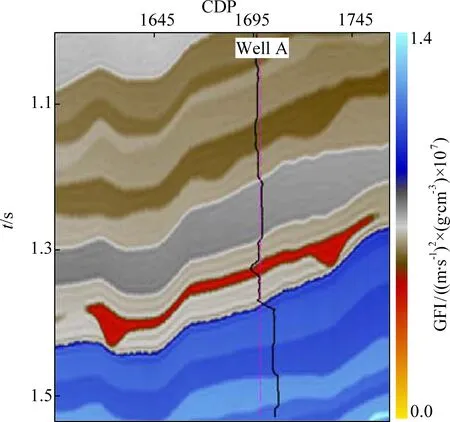
圖9 二維Gassmann流體因子模型Fig.9 2D Gassmann fluid factor model

圖11為模式1的Gassmann流體因子直接提取結果.在該模式中，分別選取層位h1和h2作為兩個約束點(在二維應用中，約束點就變成了約束線)，兩個約束點(線)的流體因子值從模型中得到，通過反復試驗，設定約束點權重α=200.可以看出，在該模式中，由于沒有初始模型的作用，因此流體因子的提取結果客觀準確.

圖12為模式2的Gassmann流體因子直接提取結果.在該模式中，分別選取層位h0、h1、h2、h3、h4作為約束點(線)，約束點的流體因子值從模型中得到，通過反復試驗，設定約束點權重α=20.該模式由于也沒有初始模型的作用，因此流體因子的提取結果較為客觀準確.

圖13b為模式3的Gassmann流體因子直接提取結果.在該模式中，使用一個極低頻模型的所有點進行約束，該極低頻模型來自于對原始模型的400次平滑處理，如圖13a所示，通過反復試驗，設定約束點權重α=0.02.可以看出，相對于模式1和模式2，模式3的流體因子提取結果分辨率和準確度略有降低，但是橫向上的穩定性卻得到了有效的提高.同時需要指出的是，在模式3中，低頻約束模型的作用只是為了穩定反演結果，并不參與反演解的迭代過程，因此，不會影響到結果的客觀準確性.

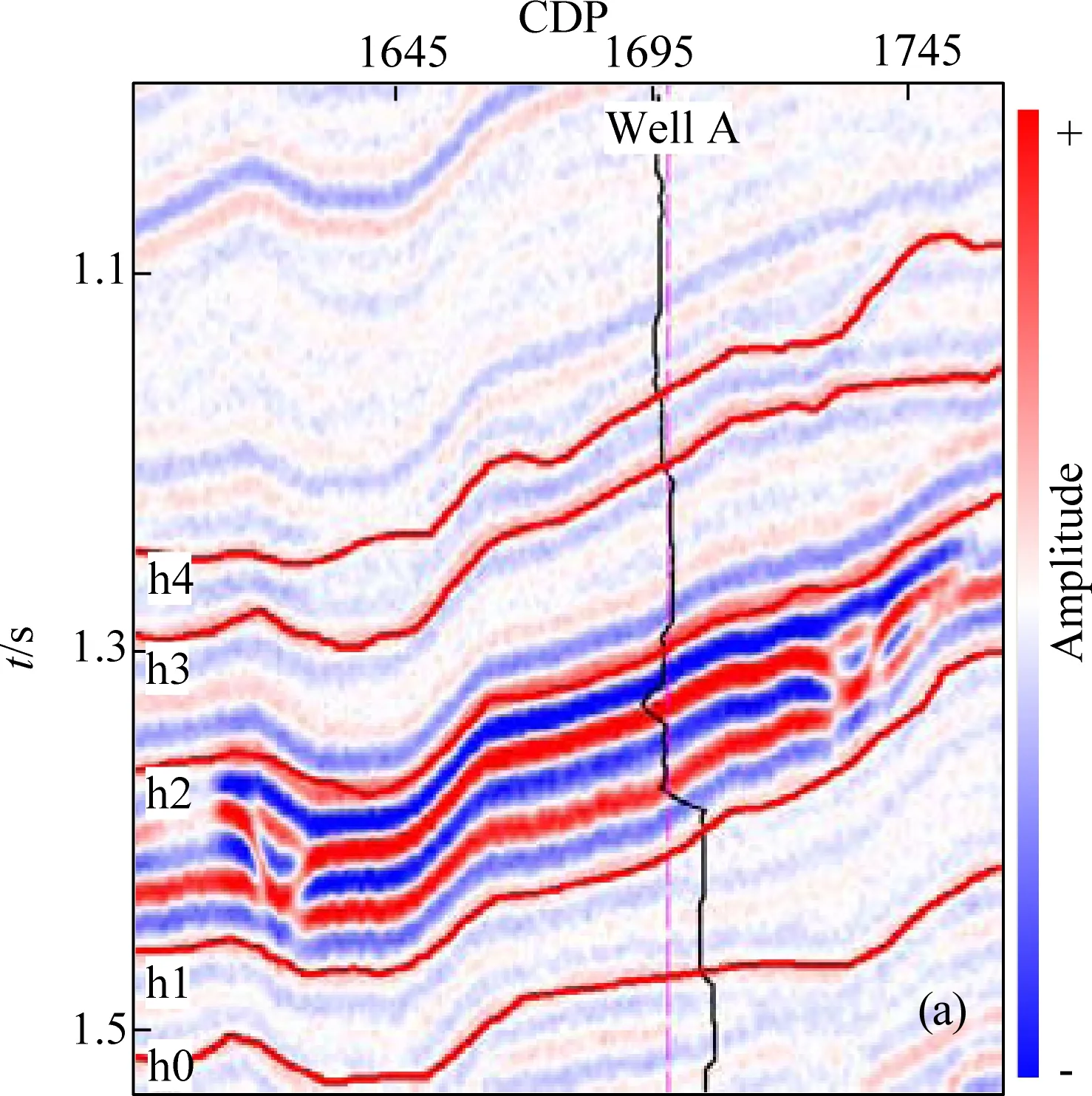
圖10 二維Gassmann模型疊加剖面(S/N=4)Fig.10 Stacked profile of 2D Gassmann model(S/N=4)

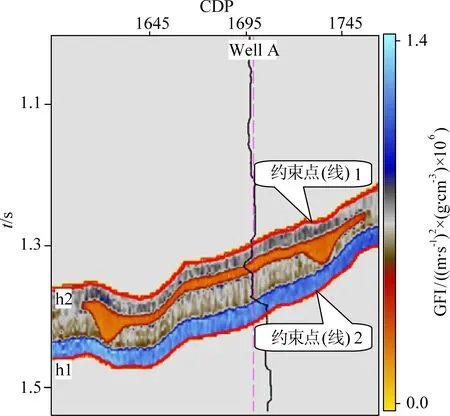
圖11 二維模式1提取結果Fig.11 2D Extraction result with pattern 1

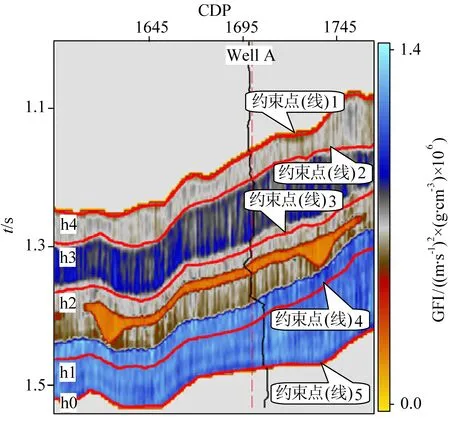
圖12 二維模式2提取結果Fig.12 2D Extraction result with pattern 2

從提取效果可以看出，該方法類似于基于模型的方法，但是與模型反演又是不相同的，基于模型的反演方法受模型的影響比較大，且分辨率會比較低，而該方法的靈活度高，且受模型影響的程度小，其優點是可以控制模型對反演結果的影響，在穩定性和分辨率之間尋求一個平衡.

4.4 約束模式選取原則

一般來說，模式1適合于約束層位間時間段比較小的情況，即屬于一種針對目標體的提取模式.實際應用中總結發現，當反演時間段大于一個子波的長度，而小于兩個子波的長度時，應用模式1會有較好的效果.

模式2可以看成是模式1的不同組合形式，即模式2可以用多個不同的層位作為約束點，進行約束，該方法適用于解釋的層位比較多的研究工區.

模式3使用約束模型的所有點進行約束，模式3更適合于約束層位間時間段比較大的、信噪比低的地震資料的流體因子提取.同時，如果反演的數據段不是很長，可以使用一個常數模型進行點約束，也會有很好的反演結果，即認為在這個時間段內地層的流體因子的變化趨勢是個常數.

在實際應用中，對于點約束的模式怎么選取并沒有什么規則可言，可嘗試不同的約束模式進行約束，并分析不同模式的提取結果和效果.最后需要指出的是，這三種約束模式是最常用的，但并不是唯一的，也可以根據工區的實際情況來制定不同的約束模式，此時只需要改變點約束的矩陣方程即可，或是將這三種模式進行組合使用，同樣會有很好的效果.

5 實際應用與分析

流體因子直接提取實際應用來自勝利油田埕島地區，工區主力含油層系是新近系，是目前勘探開發的熱點地區.

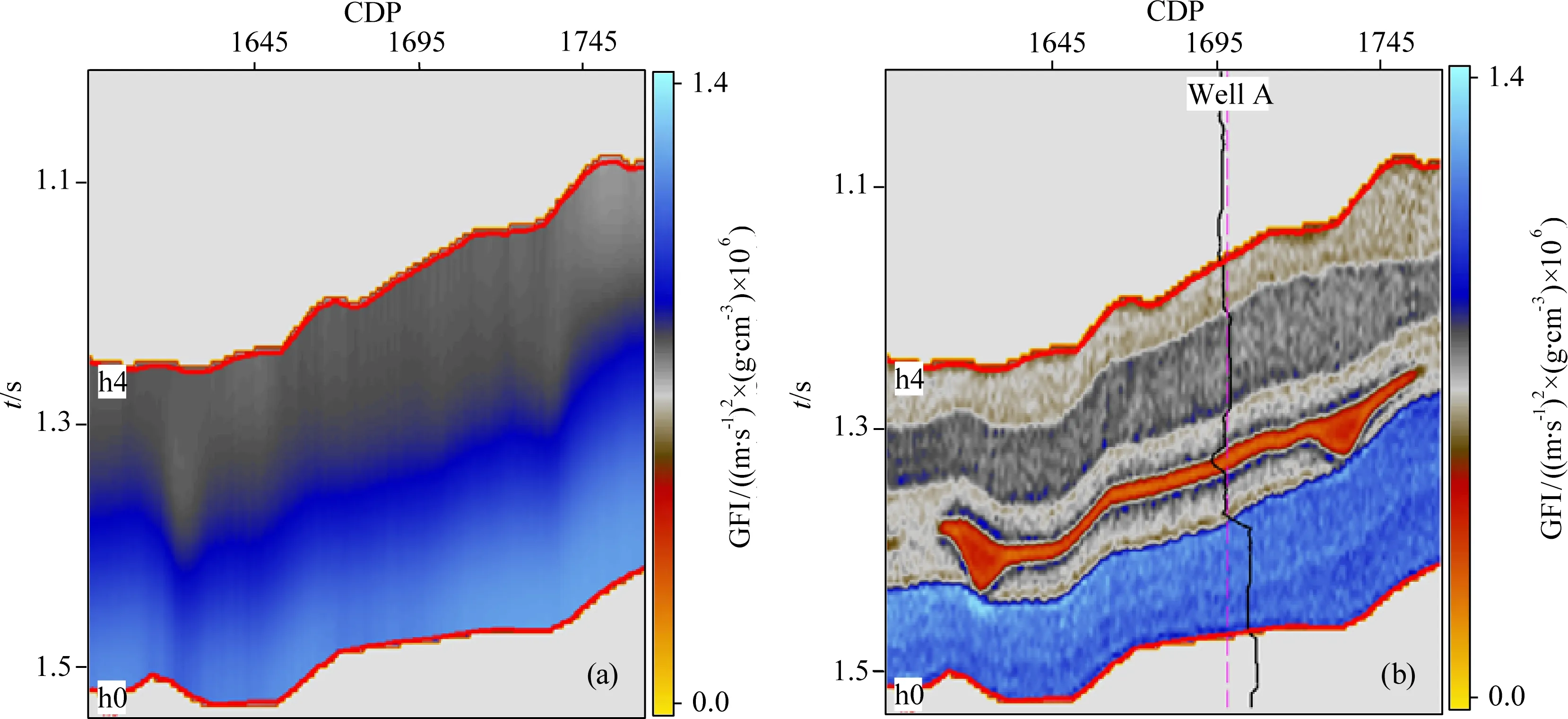
圖13 二維模式3提取結果(a) 約束所用的極低頻模型；(b)提取結果.Fig.13 2D Extraction result with pattern 3(a) Extremely low frequency model；(b) Extraction result.

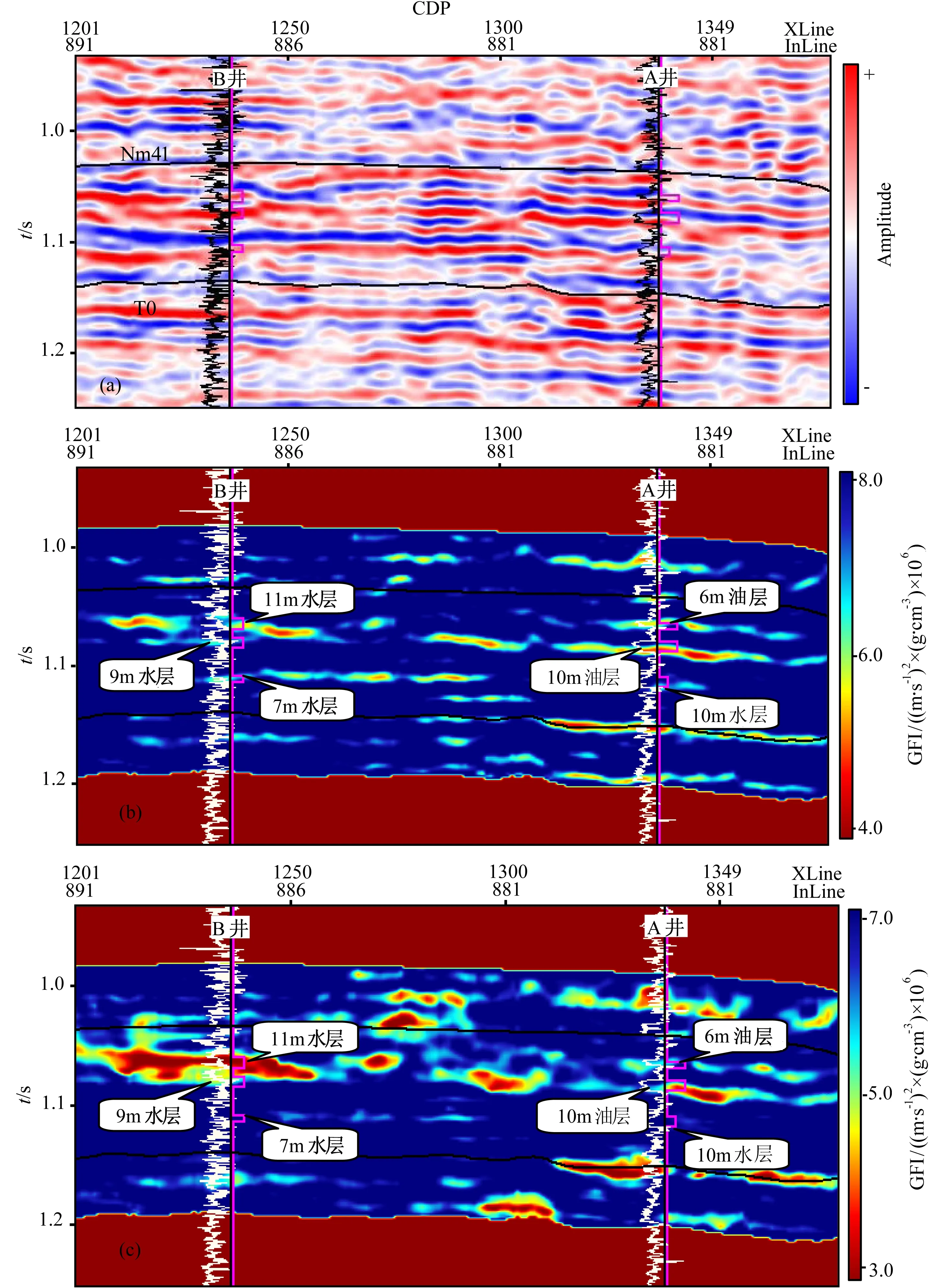
圖14 Gassmann流體因子提取剖面(a) 疊后地震剖面；(b) 直接提取結果；(c) 間接提取結果.Fig.14 Gassmann fluid factor extraction profiles(a) Poststack seismic section；(b) Direct extraction；(c) Indirect extraction.

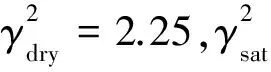
進一步將流體因子直接提取的結果和間接求取的結果進行了對比分析.圖14a為疊后地震剖面，黑色曲線為伽瑪測井曲線，粉紅色曲線為油水指示曲線，地震反射屬于中強度振幅，信噪比較低，很難通過疊后亮點或是分頻技術有效的識別含油氣性；圖14b為Gassmann流體因子直接提取的結果，圖14c為間接提取的結果，其中白色曲線為伽瑪曲線.對于A井，井旁道1.06s和1.077s處分別有一個6m、10m的油層，1.11s處有一水層，圖14b的流體因子直接提取結果在這三處都表現為低值，并且油層的流體因子相對于水層的流體因子更低一些.而圖14c的流體因子間接提取結果對于6m油層的反映并不明顯，對于10m的水層沒有反映.

對于B井，井旁道1.055s處、1.075s處、1.105s處分別有一個11m、9m、7m的水層，圖14b的流體因子直接提取結果對于這三處都能較好的識別，而圖14c的流體因子間接提取結果只是在1.06s處有個很低的值，對于上面的兩個水層，也沒有分開，分辨率明顯低于流體因子直接提取的結果.

通過以上的對比可以看出，流體因子在油層、水層處都表現為低值，但是油層的流體因子相對于水層的流體因子會更低一些.

通過提取兩個數據體的沿層結果進行比較，來進一步對比和分析本文所提出的方法的有效性和先進性.如圖15所示，圖15a為本文方法的流體因子直接提取結果，圖15b為流體因子間接提取的結果，沿層結果為拾取的Nm41層位往下40ms的流體因子均方根振幅值.本工區目的層系為河流相儲層，流體因子直接提取的結果(圖a)很好地展現了河流相砂體儲層的形態，準確度高.然而，相比于流體因子直接提取的結果，流體因子間接提取結果(圖b)并沒有較好地展現河道砂體儲層的形態，特別是B井在沿層切片上也表現出很低的流體因子值，與實鉆結果不吻合，準確度不高.

從實際應用結果可以看出，相對于間接提取的方法，本文提出的Gassmann流體因子直接提取結果的分辨率更高、準確性更好，從而實現了不同流體的有效區分，并且能夠與已知的流體解釋結果很好地匹配，說明本文提出的算法是準確可靠的.

圖15 Gassmann流體因子提取結果的沿層切片(a) 直接提取結果；(b) 間接提取結果.Fig.15 Layer-along slices of extracted Gassmann fluid factor(a) Direct extraction；(b) Indirect extraction.

6 結論

(1) 本文提出的可變點約束Gassmann流體因子直接提取算法約束過程靈活，可以使用兩個點，也可以使用多個點進行約束，可以使用較精確的模型進行約束，也可以使用極低頻模型進行約束，并可以通過調節α的大小來控制點約束的權重.

(2) 由于最大程度的弱化了對于反演初始模型的依賴，因此提取過程更加客觀準確，并且提取結果的穩定性好，實際應用范圍也更加廣泛，益于進一步的推廣應用.

(3) 該方法不僅可以提取Gassmann流體因子，也可以提取其它類型的流體因子，此時只需得到該流體因子的近似方程，而可變點約束的模式和原則不用改變.

Bosch M, Mukerji T, González E F. 2010. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics: A review.Geophysics, 75(5): A165-A176.

Buland A, Omre H. 2003. Bayesian linearized AVO inversion.Geophysics, 68(1): 185-198.

Chi X G, Han D H. 2006. Fluid property discrimination by AVO inversion. // 76th Annual Meeting, SEG Expanded Abstracts, 2052-2056.

Connolly P. 1999. Elastic impedance.TheLeadingEdge, 18(4): 438-452.

Downton J E. 2005. Seismic parameter estimation from AVO inversion[Ph. D. thesis]. Calgary: University of Calgary.

Fatti J L, Smith G C, Vail P J, et al. 1994. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique.Geophysics, 59(9): 1362-1376.

Goodway B, Chen T, Downton J. 1997. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters. // 67th Annual meeting, SEG, Expanded abstracts, 183-186. Gray D. 2002. Elastic inversion for Lame parameters. 72th Annual Meeting, SEG, Expanded Abstracts, 213-216.

Haas A, Dubrule O. 1994. Geostatistical inversion—A sequential method of stochastic reservoir modeling constrained by seismic data.FirstBreak, 13(12): 561-569. Hampson D. 1991. AVO inversion, theory and practice. The Leading Edge, 10: 39-42.Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data.Geophysics, 52(9): 1211-1228.

Ning Z H, He Z H, Huang D J. 2006. High sensitive fluid identification based on seismic data.GeophysicalProspectingforPetroleum, 45(3): 239-242.

Quakenbush M, Shang B, Tuttle C. 2006. Poisson impedance.TheLeadingEdge, 25(2): 128-138.

Russell B H, Gray D, Hampson D P. 2011. Linearized AVO and poroelasticity.Geophysics, 76(3): C19-C29.

Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassmann perspective.Geophysics, 68(1): 29-39.Shi Y M, Zhao W Z, Cao H. 2007. Nonlinear process control of wave-equation inversion and its application in the detection of gas.Geophysics, 72(1): R9-R18.

Simmons J L, Backus M M. 1996. Waveform-based AVO inversion and AVO prediction error.Geophysics, 61(6): 1575-1588.

Smith G C, Gidlow P M. 1987. Weighted stacking for rock property estimation and detection of gas.GeophysicalProspecting, 35(9): 993-1014.

Smith G C, Gildow P M. 2000. A comparison of the fluid factor withλandμin AVO analysis. // 70th Annual Meeting, SEG, Expanded Abstracts, 1940-1945.

Tarantola A. 2005. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia: Society for Industrial and Applied Mathematics.

Ulrych T J, Sacchi M D, Woodbury A. 2001. A Bayes tour of inversion: a tutorial.Geophysics, 66(1): 55-69.

Wang B L, Yin X Y, Zhang F C. 2005. Elastic impedance inversion and its application.ProcessinGeophysics(in Chinese), 20(1): 89-92. Whitcombe D N. 2002. Elastic impedance normalization.Geophysics, 67(1): 60-62.Yang P J. 2008. Seismic wavelet blind extraction and non-linear inversion[Ph. D. thesis] (in Chinese). Dongying: China University of Petroleum.Yang P J, Yin X Y. 2008. Non-linear quadratic programming bayesian prestack inversion.ChineseJ.Geophys. (in Chinese), 51(6): 1876-1882, doi: 10.3321/j.issn:0001-5733.2008.06.030.

Yin X Y, Yang P J. 2008. A Novel Prestack AVO Inversion and Application. // 78th Annual Meeting, SEG, Expanded Abstracts, 2041-2044.Yin X Y, Zhang S X, Zhang F. 2013a. Delicate construction of fluid factor and its application based on two-phase media theory.ProcessinGeophysics(in Chinese), 28(6): 2911-2918, doi: 10.6038/pg20130611.

Yin X Y, Zhang S X, Zhang F. 2013b. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification.ChineseJ.Geophys. (in Chinese), 56(7): 2378-2390, doi: 10.6038/cjg20130724.

Zhang S X. 2012. Methodology and application of fluid identification with seismic information[Ph. D. thesis] (in Chinese). Dongying: China University of Petroleum. Zheng J J, Yin X Y, Zhang G Z. 2011. Fluid factor analysis and the construction of the new fluid factor.ProcessinGeophysics(in Chinese), 26(2): 579-587, doi: 10.3969/j.issn.1004-2903.2011.02.024.

Zong Z Y, Yin X Y, Wu G C. 2012. Fluid identification method based on compressional and shear modulus direct inversion.ChineseJ.Geophys. (in Chinese), 55(1): 284-292, doi: 10.6038/j.issn.0001-5733.2012.01.028.

附中文參考文獻

寧忠華, 賀振華, 黃德濟. 2006. 基于地震資料的高靈敏度流體識別因子. 石油物探, 45(3): 239-242.

王保麗, 印興耀, 張繁昌. 2005. 彈性阻抗反演及應用研究. 地球物理學進展, 20(1): 89-92.

楊培杰. 2008. 地震子波盲提取與非線性反演[博士論文]. 東營: 中國石油大學.

楊培杰, 印興耀. 2008. 非線性二次規劃貝葉斯疊前反演. 地球物理學報, 51(6): 1876-1882, doi: 10.3321/j.issn:0001-5733.2008.06.030.

印興耀, 張世鑫, 張峰. 2013a. 雙相介質理論指導下的流體因子精細構建與應用. 地球物理學進展, 28(6): 2911-2918, doi: 10.6038/pg20130611.

印興耀, 張世鑫, 張峰. 2013b. 針對深層流體識別的兩項彈性阻抗反演與Russell流體因子直接估算方法研究. 地球物理學報, 56(7): 2378-2390, doi: 10.6038/cjg20130724.

張世鑫. 2012. 基于地震信息的流體識別方法研究與應用[博士論文]. 東營: 中國石油大學.

鄭靜靜, 印興耀, 張廣智. 2011. 流體因子關系分析以及新流體因子的構建. 地球物理學進展, 26(2): 579-587, doi: 10.3969/j.issn.1004-2903.2011.02.024.

宗兆云, 印興耀, 吳國忱. 2012. 基于疊前地震縱橫波模量直接反演的流體檢測方法. 地球物理學報, 55(1): 284-292, doi: 10.6038/j.issn.0001-5733.2012.01.028.

(本文編輯 張正峰)

Direct extraction of the fluid factor based on variable point-constraint

YANG Pei-Jie1,2, WANG Chang-Jiang1, BI Jun-Feng1, LIU Shu-Hui1

1GeoScienceResearchInstituteofShengliOilfield,SINOPEC,Dongying257015,China2PostdoctoralWorkstationofShengliOilfield,SINOPEC,Dongying257015,China

Fluid factor extraction plays an increasing important role in fluid discrimination. The conventional way of such extraction through prestack inversion is to calculate fluid factors indirectly from P-wave velocity, S-wave velocity and density data which can be derived from inversion of seismic data. However, this method has two disadvantages. One is that the density data imbedded in fluid factors is more contaminated by noise than the inverted P-wave and S-wave reflectivity even with large incident angles. The other is that the indirect way of fluid factor estimation can create more uncertainties caused by the indirect calculation. This article focuses on the direct extraction of Gassmann fluid item (GFI), which is the real factor that reflects the influence of fluid in porous rock as Russell et al. discussed. The objective is to improve accuracy and stability of fluid factor extraction compared with the conventional way.A novel method for direct extraction of fluid factors, named variable point-constraint fluid factor direct extraction (VPC-FFDE), is developed that uses variable point-constraint strategy to extract GFI the Gassmann fluid item from prestack data directly. The initial objective function is build combining likelihood function, priori information and GFI approximate equation. The final objective function is yielded by adding a variable number of constraint points to the initial objective function. Three different point-constraint patterns are examined, and different constraint effects are illustrated using synthetic data. Instead of the initial model, this method uses a constraint model to improve the accuracy and stability of the extraction results. The core of the proposed approach is to control the extraction results by adding a variable number of constraint points into the extraction process. Either accurate constraint points or the extremely low frequency model can be used, and different numbers of constraint points can be chosen during the constraint process. It does not need to obtain P-wave velocity, S-wave velocity and density first, and therefore can avoid accumulation of errors that often appear with indirect approach.We applied the proposed method to the Chengdao area of the Shengli Oilfield, Sinopec. The area is about 150 km2. We chose prestack angle stacks in this case. Neither the structural high nor the bright spot is unambiguous for the prediction of gas or oil sands in this area, and the SNR is also a little low. We used a constant value constraint model to constrain the extraction process and pattern 3 was chosen in this example. As can be seen from the extraction results, the direct GFI extraction profile in the three layers are all characterized by low values, but the GFI value of the oil layer is relatively lower compared to the water layer, which has already been verified in the fluid substitution model in the previous section. This result gives a clear indication of the lateral extent and vertical extent of the oil layer and water layer. The extraction results are consistent with current oil production and joint interpretation results with only well information. However, the indirect GFI extraction result is somewhat more ambiguous, and the resolution is also lower. The actual application results show that compared with the indirect GFI extraction results, the direct ones have higher resolution and accuracy, and can match the well logging interpretation results perfectly. We implemented the procedure to distinguish different fluids. The proposed method is accurate and reliable. We implemented the purpose of more accurate fluid discrimination through fluid factor direct extraction.We proposed a novel approach to extract GFI directly based on GFI linearized approximation, Bayesian inversion framework and variable points-constrain strategy. The likelihood function and priori information contribute to the high extraction resolution. The strategy of variable points-constraint renders the extraction process more stable and not sensitive to the constraint model. Model validation and actual application results show that the proposed method can produce good application effects even if the SNR of prestack data is low, and therefore is beneficial for further popularization and application.

Fluid Factor; Prestack Inversion; Variable Point Constraint; Direct Extraction; Objectivity; Stability

10.6038/cjg20150631.

國家科技重大專項“渤海灣盆地精細勘探關鍵技術”(2011ZX05006) 資助.

楊培杰，男，1972年生，2008年博士畢業于中國石油大學(華東)，現為勝利油田勘探開發研究院高級工程師，博士后，主要從事地震地質綜合解釋研究.E-mail:yangpeijie.slyt@sinopec.com

10.6038/cjg20150631

P631

2014-02-14，2015-05-06收修定稿

楊培杰， 王長江， 畢俊鳳等. 2015. 可變點約束疊前流體因子直接提取方法.地球物理學報，58(6):2188-2200,

Yang P J, Wang C J, Bi J F, et al. 2015. Direct extraction of the fluid factor based on variable point-constraint.ChineseJ.Geophys. (in Chinese),58(6):2188-2200,doi:10.6038/cjg20150631.