基于拆卸序列優化的零部件拆卸分析系統

王哲

（合肥工業大學機械與汽車工程學院，合肥230009）

0 引言

拆卸是采用一定的工具和手段，解除對零件造成約束的各種聯接，將產品零部件逐個分離的過程。拆卸序列規劃的定義為，在滿足產品結構和裝配關系等要求的前提下，生成零件拆卸序列的過程［1］。為了獲得能夠滿足裝配約束要求的拆卸序列，并對拆卸序列進行優化，提高拆卸效率及其使用價值，本文提出了基于拆卸混合圖的拆卸序列優化模型［2］，并在獲得滿足要求的拆卸序列后使用遺傳算法進行優化求解。為了方便裝配件拆卸信息的管理及拆卸序列的優化，編寫了拆卸分析系統，通過它可以計算得到近似最優序列。

1 拆卸序列模型

1.1 拆卸信息模型

本文考慮的產品拆卸信息模型主要包括三個部分：零件基本信息、拆卸過程信息及裝配信息。零件基本信息主要包括該零件的名稱、體積、重量等具體信息；拆卸過程信息即所使用的拆卸工具、拆卸時間等信息；而裝配信息則主要是考慮零件拆卸過程中的約束關系。

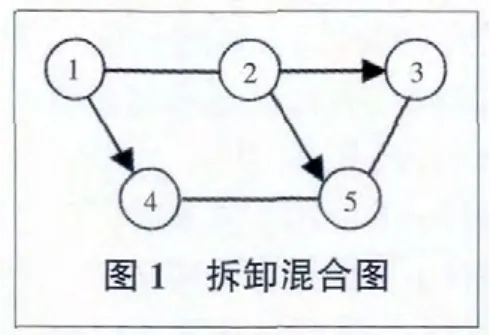
根據以上拆卸信息模型采用混合圖進行建模。拆卸混合圖是一種常用的拆卸信息建模方法，如圖1所示。混合圖的頂點定義為產品的零件或部件，有向邊或無向邊分別表示了零部件之間的裝配約束關系。

拆卸混合圖可以用集合形式表示為

式中：G 為混合圖集合；V=｛v1，v2，…，vn｝表示零部件集合；UE=｛ue1，ue2，…，uen｝是無向邊集合，表示零件之間無接觸約束關系；DE=｛de1，de2，…，den｝為有向邊集合，表示零件之間存在拆卸優先關系，即有接觸約束關系。

拆卸混合圖可以很清楚地反映出零件直接的拆卸約束關系，但是計算機是無法直接識別這類圖模型的，因此必須對其進行數字化處理。本文采用連接矩陣和優先矩陣來表達。

即可將混合圖 G=｛V，UE，DE｝分解為 GC=｛V，UE｝和GP=｛V，DE｝。對于連接矩陣

其中，

特別規定當i=j時，cij=0。

對于連接矩陣

其中，

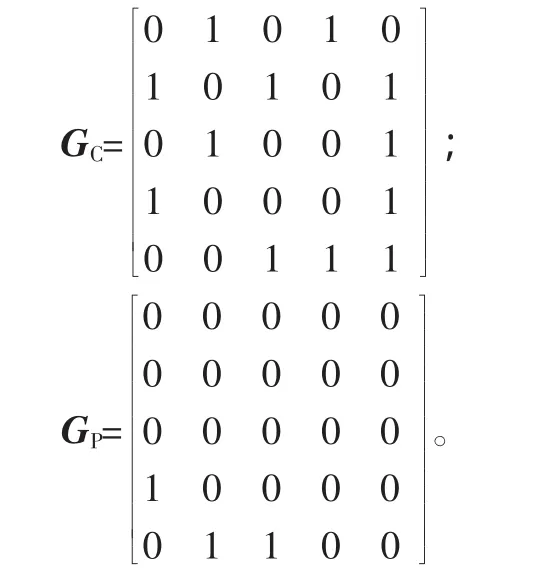
對于如圖1所示拆卸混合圖即可表示為：

1.2 拆卸序列生成

拆卸序列的生成基于定向搜索策略，即在優先關系矩陣的引導下，生成拆卸序列。具體流程如圖2所示。

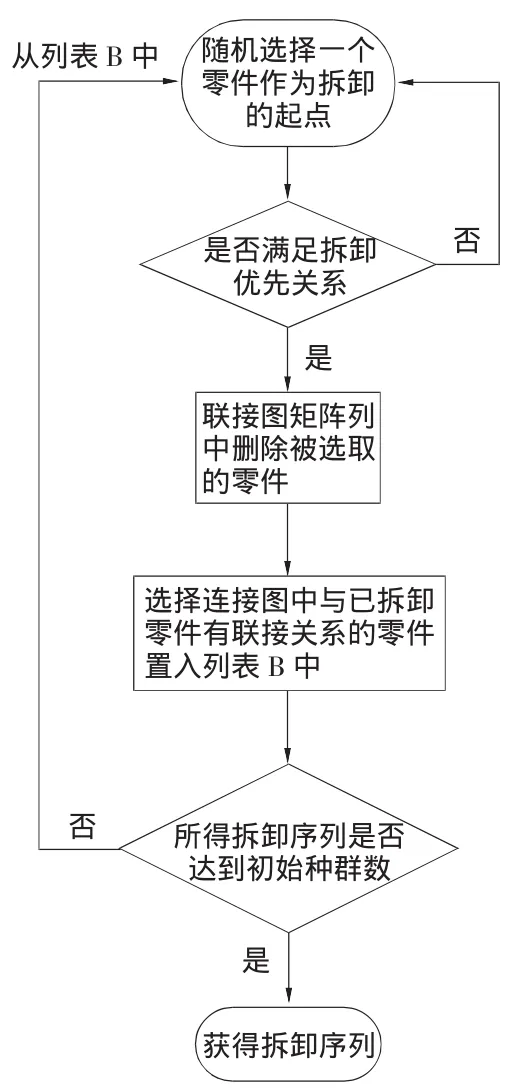
圖2 拆卸序列生成圖

驗證表明隨機選取零件作為拆卸的起始點比指定初始拆卸零件速度要快很多，其關鍵在于拆卸優先關系的合理定義和全面表述。根據此流程產生的拆卸序列作為初始序列能夠滿足拆卸的優先關系，因此初始序列是合理可行的。通過此方法能夠快速地生成足量的初始拆卸序列。

1.3 拆卸序列的優化

影響拆卸效率的兩個主要因素是拆卸方向的變更次數與拆卸工具的更換次數，因此拆卸序列的優化函數構建應主要考慮這兩方面。對于所得拆卸序列s，構建的適應度計算公式如下：

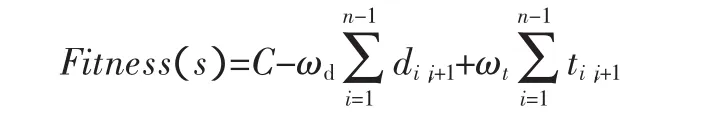
其中：ωd和ωt分別代表拆卸方向和拆卸工具的權重，n為拆卸序列中所含零件總數，常數C為保證適應度隨著時間增大而減小。對于 di，i+1和 ti，i+1，則有：

2 拆卸序列優化模型求解

拆卸序列規劃實際上是一個NP組合優化的問題，傳統的拆卸序列規劃方法大多是基于圖搜索的方法，但是圖搜索算法存在其弊端，即隨著被拆卸深度的增加，無法規避組合爆炸問題。

遺傳算法無需遍歷整個搜索空間就能夠得到最優或是次最優解，就能夠很好地解決組合爆炸問題。遺傳算法是由美國Michigan大學的John Holland與其同事、學生們基于生物進化論中的自然選擇和群體遺傳學規律而提出的一種優化搜索算法［3］。基本思想是：把整個待拆卸體信息庫空間映射成遺傳空間，將具體零部件信息映射成遺傳染色體，對其中的所有個體進行適應度大小的計算。之后對群體進行選擇、交叉或變異等遺傳操作，適應度小的個體自行淘汰，適應度大的個體保存下來。通過指定代數的反復操作或者達到適應度閾值后，求出最優個體。

具體算法流程圖如圖3所示。

2.1 染色體構造

在遺傳算法中把一個問題的可行解從其解空間轉換到遺傳算法所能處理的搜索空間的轉換方法稱為編碼。編碼決定了交叉、變異等遺傳運算方法，能夠極大地影響算法的運行效率。

對于零部件的拆卸序列，直接采用零件序號進行實數編碼明顯更加方便與合理。實數編碼省去了編碼和解碼的過程，更利于算法的實施。如染色體為“1，2，3，4，5”的一種拆卸序列為：1→4→2→3→5。

圖3 遺傳算法流程

2.2 交叉算子

交叉操作又稱為基因重組，就是按給定的交叉概率Pc，從群體中隨機選取2個父個體，互相替換2個父個體的其中一部分結構，之后進行重組形成新個體的操作。交叉操作是生成新個體的主要方式，能夠提高算法的全局搜索能力。本模型采用的是部分映射交叉法，即在父個體中選擇一個子序列并且在替換到另一個父個體時次序和位置盡可能不變。方式如下：

隨機父個體 1：1→2→|3→4|→5。

隨機父個體 2：1→4→|2→3|→5。

交換兩父體字串：1→2→|2→3|→5；1→4→|3→4|→5。

映射關系為：2→3→4。

映射后的子代為：1→4→|2→3|→5；1→2→|3→4|→5。

2.3 變異操作

變異是以較小的概率對染色體串上的某些位值進行改變，從而形成新的個體的過程。變異操作決定了遺傳算法的局部搜索能力，是產生新個體的輔助方法。

本模型采用的是置換變異方法，即隨機選擇2個基因，置換它們彼此在序列中的位置，并且要注意的是這種置換并不能改變零件之間的拆卸優先關系。舉例如下：

父個體 1：1→2→3→4→5。

選擇3、4進行置換后的序列為：1→2→4→3→5。

3 軟件設計

3.1 軟件設計思想

為了實現便捷地拆卸序列規劃操作，基于拆卸序列優化開發了一個計算系統。系統主要設計思想是：令使用者在輸入相對較少產品零件信息的基礎上，通過該系統可以對產品進行拆卸分析，生成拆卸序列，并對產品的拆卸序列進行回收評估，之后運用遺傳算法進行優化，得出最優或近似最優的拆卸序列。

3.2 參數選擇

本文中采用基因組的編碼方式表達裝配體中零件的信息。一個基因組封裝了零件拆卸中所有相關的信息，同時也是在數據庫中儲存的基本單元。基因組采用三位碼編碼，包括零件編號、拆卸工具、拆卸方向信息。表示如下：

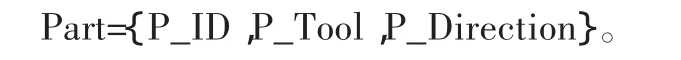
其中：PID表示零件編號，由數據庫自動生成；P_Tool表示拆卸工具編號，對應拆卸工具表中的工具；P_Direction表示拆卸方向，主要有｛+X，-X，+Y，-Y，+Z，-Z｝6個方向。

表1 Part數據庫字段表

遺傳算法中的參數選擇主要有群體規模S，交叉概率PC，變異概率Pm，終止條件等。這些參數的選擇對算法的運行性能影響較大，不恰當的選擇會導致算法運行緩慢。

群體規模S表示群體中所含個體的數量，在本模型中即為零件個數，一般的取值范圍是20～100；交叉概率PC，交叉操作是新序列生成的主要方式，所以交叉概率應取較大值，一般的取值范圍是0.4～0.99；變異概率Pm，變異概率太小會是遺傳算法趨近隨機搜索，太大又會使產生新個體能力變差，一般取值范圍是0.0001～0.1；終止條件主要是終止代數或適應度最小準則。終止代數指的是遺傳算法運行到指定的進化代數G之后就停止運行，取出群體適應度最佳的個體作為所求問題的最優解輸出；另一種終止條件是給定一個閾值C，當其連續L代的平均適應度差異小于該值時停止。

3.3 軟件結構及系統流程

系統集成了多個模塊的功能，其中產品模型信息管理、拆卸序列分析、拆卸序列優化等。系統具體工作流程如圖4所示。

實現系統邏輯的偽代碼表示如下∶

Initialize(s);//載入并初始化序列

Verify(x)

{驗證序列x是否符合拆卸優先順序}

Get_Fitness(x)

{按公式計算個體適應度值

returen Fs;}

Verify(Random(s));//隨機打亂并驗證序列s是否符合拆卸優先順序

for(i=0;Fs＜=C||i＜=G;i++)//C代表給定的終止閾值,G代表給定的進化代數

{

While(Verify(s))

{Intersect(s);//交叉操作

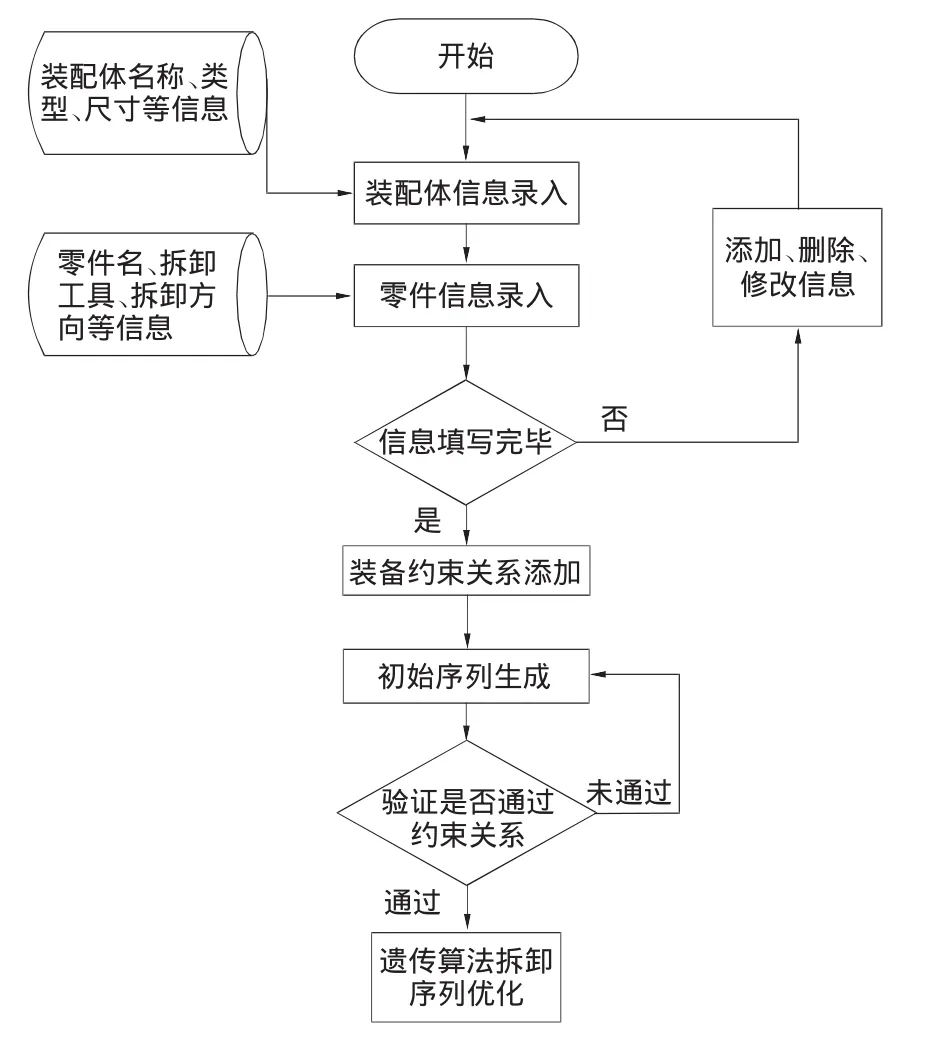
圖4 軟件邏輯流程

Mutate(s);//變異操作

Get_Fitness(s);//計算個體適應度}

}

輸出結果;

3.4 操作實例

圖5為某裝配體的裝配體信息管理界面，該裝配體由12個零件組成，界面支持裝配體信息及零件信息的添加刪除修改。

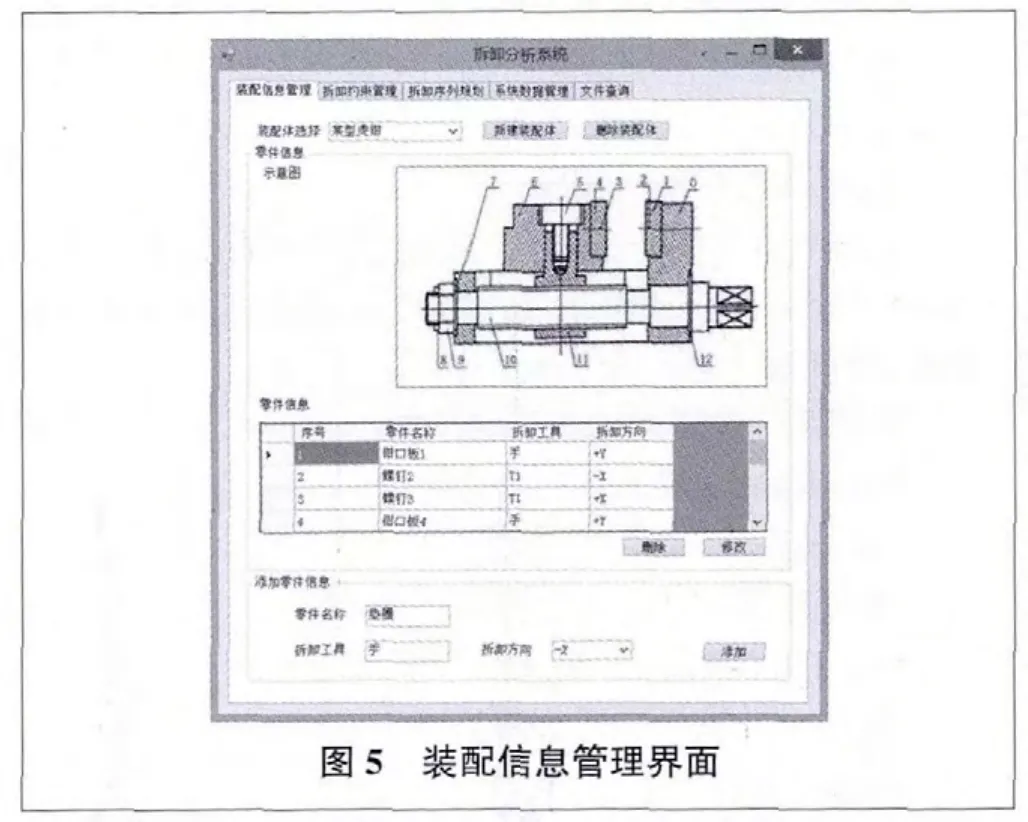
圖6為拆卸序列規劃界面，在參數設定框體中輸入預先設定的遺傳算法參數，這里取交叉概率PC=0.5，變異概率Pm=0.05，終止代數G=50，適應度閾值=180。生成初始序列為 8→9→2→10→3→4→11→1→12→7→5→6，之后點擊計算即可在滿足終止條件時生成最優或近似最優解，即 3→5→8→9→2→10→11→1→12→7→4→6。經驗證，所得拆卸序列符合約束條件且為適應度最大解，證明軟件從算法的執行上是可行的。

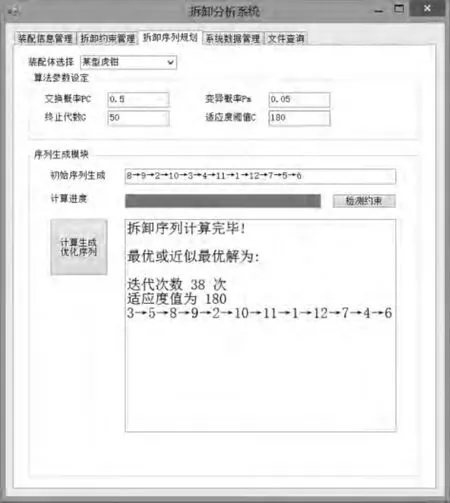
圖6 拆卸序列規劃界面

4 結語

本文提出了基于拆卸混合圖的拆卸序列優化模型，并對序列優化的適應度進行了闡述。之后給出了使用遺傳算法的拆卸序列模型求解辦法。為方便裝配件拆卸信息的管理及拆卸序列計算，編寫了拆卸分析系統，計算了實例并獲得了最優或近似最優拆卸序列，證明了軟件的可用性。能夠為裝配件信息管理及拆卸序列的智能生成提供一定的支持。

［1］ 劉志峰，胡迪，高洋，等.基于貪婪算法的產品拆卸序列規劃［J］.中國機械工程，2011（18）：2162-2166.

［2］ Zhang H C，Kuo T C.A Graph-Based Approach to Disassembly Model for End-of-Life Product Recycling［C］//IEEE/CPMT International Electronics Manufacturing Technology Symposium，1996：247-254.

［3］ 韓建升.基于遺傳算法的拆卸序列規劃研究［D］.武漢：華中科技大學，2007.

［4］ Silveira L R，Tanscheit R，Vellasco M.Quantum-Inspired Genetic Algorithms applied to Ordering ombinatorialptimization Problems［C］//WCCI2012IEEEWorld Congresson Computational Intelligence June，10-15，2012，Brisbane，Australia.

［5］ 張秀芬，張樹有.基于粒子群算法的產品拆卸序列規劃方法［J］.計算機集成制造系統，2009（3）：508-514.

［6］ 江吉彬，劉志峰，劉光復.基于工程語義信息的拆卸序列規劃算法研究［J］.計算機集成制造系統，2006（4）∶625-629.

［7］ 趙樹恩，李玉玲.模糊推理Petri網及其在產品拆卸序列決策中的應用［J］.控制與決策，2005（10）∶1181-1184，1188.

［8］ 章小紅，李世其，王峻峰，等.基于蟻群算法的單目標選擇性拆卸序列規劃研究［J］.計算機集成制造系統，2007，13（6）∶1109-1114.

［9］ 謝歆，趙國華.Visual C++高級編程實例精解［M］.北京∶國防工業出版社，2001.