基于有限元的過盈配合平均接觸壓力求解

沈健， 朱亞軍， 周丹， 劉光復， 杜曉東

（合肥工業大學，合肥230009）

0 引言

過盈配合是一種常見的連接方式，具有結構緊湊、對中性好、承載能力大、耐沖擊性好等優點。工程中通常按照彈性力學厚壁圓筒理論進行設計計算，理論計算時忽略了軸向應力，只考慮法向應力和周向應力，法向應力即接觸壓力。

過盈配合構件工作時，依靠過盈量產生的接觸壓力傳遞扭矩和軸向力，傳遞扭矩很大時設計的過盈量就需要很大，接觸壓力也相應很大。由于一些場合下過盈配合需要拆解，在應用上認為拆解時所需的拆解力是由于接觸壓力和摩擦因數導致的，且是線性關系，因此得到平均接觸壓力就可以得到宏觀拆解力。有限單元法能很好地解決過盈配合接觸的計算問題，并可以求解各種耦合問題，為實際問題的求解提供了有效的方法。

1 采用有限單元法計算過盈配合平均接觸壓力

1.1 過盈配合接觸問題的有限元求解方法

過盈配合是一種典型的非線性接觸行為，接觸問題的算法有罰函數法、拉格朗日法、增強拉格朗日法。罰函數法是計算每一載荷子步時,先檢查接觸面和目標面是否有穿透，若有穿透則在接觸面間引入法向接觸應力，其值大小與接觸剛度和穿透深度成正比。拉格朗日法是把接觸力作為一個獨立的自由度，可以實現穿透為零的真實接觸條件。但由于自由度增加會降低計算效率，增強拉格朗日法是不斷更新接觸剛度的罰函數，直到計算的穿透值小于允許值為止，該算法總體剛度矩陣較少出現病態，接觸單元接觸剛度取值更合理。本文采用增強拉格朗日法進行求解。

1.2 有限單元法的設置和求解

根據以上接觸問題計算方法的原理，建立三維模型導入有限元軟件Workbench中，仿真計算基于靜力模塊進行，設置接觸為摩擦接觸，添加摩擦因數，有限元模型的過盈量通過接觸單元實常數過盈的方法進行設置，以輸入offset（偏移量）的值來實現，設置固定約束面。設置時為了方便單元應力的提取，手動設置內孔面為接觸面（contact174），軸表面為目標面。

經過有限元計算可以得到各單元受力情況和受力單元數目，當接觸單元都受力時，平均接觸壓力是所有接觸單元的接觸壓力值的平均值。當受力單元數小于接觸面單元數時，采用將各受力單元面積乘以各單元接觸壓力再求和得到總接觸力，總接觸力除以接觸面的總面積得到平均接觸壓力。以下用實例來說明該計算過程。

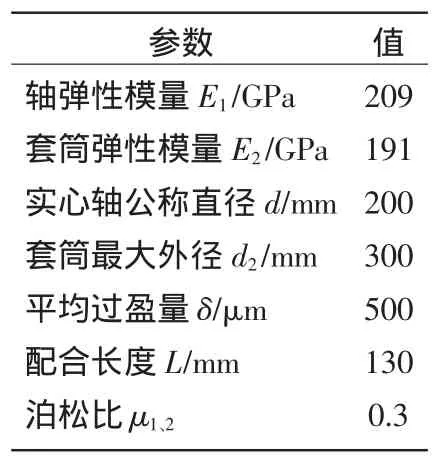
表1 軸和套筒的參數

2 計算實例

2.1 軸和套筒過盈配合平均接觸壓力的計算

給定軸和套筒的過盈配合模型如圖1所示，其各項參數如表1所示，設摩擦因數為0.1，過盈量為0.5 mm，添加圖1所示固定約束，對軸和葉輪裝配體進行自由網格劃分，設置軸和葉輪網格尺寸為15 mm，接觸面單元的網格大小為5 mm，設置內孔面為接觸面（contact174）。對模型求解，得到896個接觸單元都受法向應力，直接對各接觸單元的法向應力求平均值即可得到平均接觸壓力，為132.2 MPa。

圖1 軸和套筒約束模型

計算過盈配合接觸壓力的理論公式［4］為

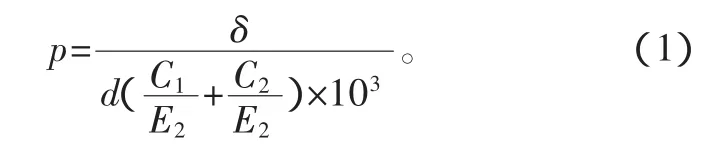
式中：C1為軸的剛性系數為套筒的剛性系數為平均過盈量，μm，d 為軸孔的公稱直徑mm；d1為空心軸內孔徑，實心軸為0。

該公式以理想狀態的軸和套筒配合為基礎。將表1中的參數帶入式（1）可以求得接觸面間的接觸壓力為135 MPa。比較有限元計算結果和式（1）的計算結果，相對誤差為2.2%，因此上述有限單元法求解的平均接觸壓力與理論計算結果相吻合。由此可見，有限單元法能很好地解決過盈配合的計算問題。

對于工程中大量復雜結構的過盈配合問題（如軸和葉輪），已沒有相應的理論計算公式，但采用上述的有限元方法的計算結果是可信的。

2.2 存在形狀誤差的軸和葉輪過盈配合平均接觸壓力的計算

2.2.1 軸的彎曲幾何模型建立

大型離心壓縮機的軸和葉輪通過大過盈配合（如φ225H7/y6）來傳遞扭矩，葉輪結構復雜，其基本參數如表2所示。

表2 葉輪的基本參數

軸在整個生產、服役周期內，容易產生彎曲，在葉輪需要修復時，要對葉輪進行加熱拆解處理，因此需要對拆解過程的接觸情況進行分析。為研究方便，將軸存在彎曲時配合模型簡化成如圖2所示，將配合面中部的彎曲量設為最大，用軸線的直線度來反映其彎曲程度，設直線度誤差為0.05 mm。

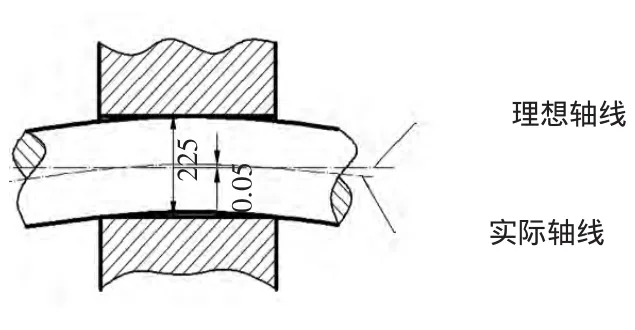
圖2 軸彎曲時的配合模型

2.2.2 有限單元法求解的設置

計算接觸壓力時的相關材料屬性、接觸和網格劃分的設置與上述軸和套筒的模型相同，將圖3中X軸負方向的端面添加面固定約束，得到接觸面（contact174）單元個數約為7700個。兩個配合面之間的接觸壓力來源于設置的過盈量和軸的直線度誤差形成的實際過盈量。

圖3 軸和葉輪有限元網格劃分

模擬加熱拆解過程，采用瞬態熱-結構耦合進行計算，添加材料的熱力學性能參數（見表3），實際加熱方式為流道面加熱，溫度載荷350℃，加熱時間為1 000 s。

2.2.3 有限單元法計算結果分析

通過有限元計算得到以下情況的接觸壓力分布云圖，如圖4～圖7所示。

表3 軸和葉輪的熱力學性能參數

圖4 不受熱、軸無直線度誤差時的接觸壓力云圖

圖5 不受熱、軸的直線度誤差為0.05 mm時的接觸壓力云圖

圖6 受熱、軸無直線度誤差時接觸壓力云圖

圖7 受熱、軸的直線度誤差為0.05 mm時的接觸壓力云圖

對比圖4和圖5，可以得到接觸壓力直觀的分布情況，接觸壓力最大的區域為中間部位，這是由于中間區域葉輪剛度最大導致的；當軸的直線度誤差為0.05 mm時，會嚴重影響葉輪上的接觸壓力分布狀況，接觸壓力最大的區域會向實際過盈量最大的部位移動；軸的直線度誤差為0.05 mm時的最大接觸壓力大于無直線度誤差狀態下的最大接觸壓力。

對比圖4和圖6，受熱時接觸壓力的分布相對于不受熱時變化很大，配合面靠葉輪進氣口處（配合面最右端）的接觸壓力最大。圖6、圖7所示中心區域接觸壓力很小，圖7中部分接觸區域接觸壓力幾乎為0。

針對得到的計算結果圖4和圖5，采用ANSYS后處理技術，提取接觸單元的接觸壓力，應用MATLAB編程連成曲面，建立表面接觸壓力分布曲面如圖8和圖9所示。設定該曲面的3個坐標分別為配合面軸向尺寸、圓周方向偏轉角度、接觸壓力的數值。

由圖8、圖9可知：1）軸無直線度誤差時，過盈配合接觸壓力的分布隨著軸向尺寸的變化而變化，接觸壓力的最大值出現在圖4所示葉輪距離左端面42 mm處，接觸壓力沿圓周方向的變化不大；2）軸的直線度誤差為0.05mm時，應力分布發生變化，應力隨軸向位置和偏轉角度的不同變化較大。最大接觸壓力出現在圖5所示葉輪距離左端面42 mm處，周向偏轉角度為0°。

圖8 軸無直線度誤差的接觸壓力曲面

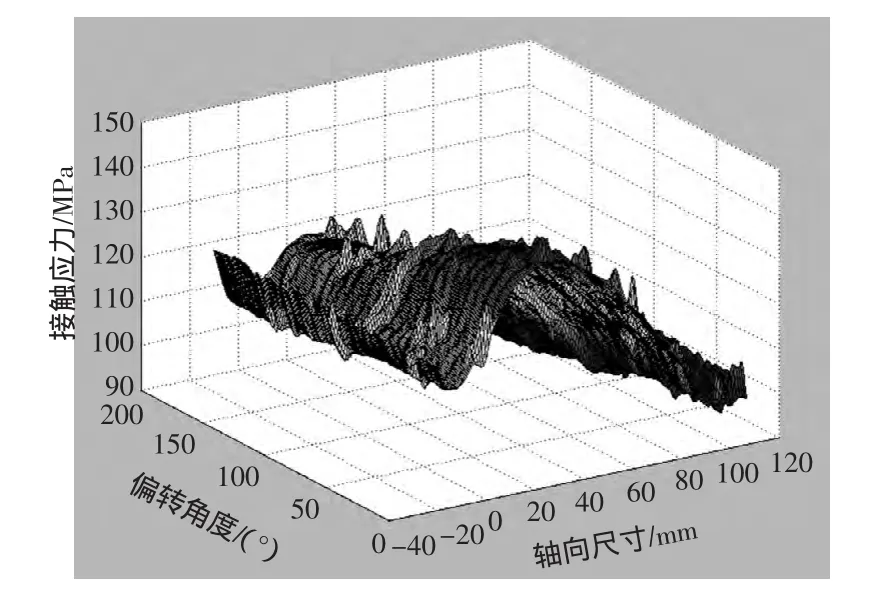
圖9 軸的直線度誤差為0.05 mm時的接觸壓力曲面

分別建立存在不同的直線度誤差的軸和葉輪裝配的有限元模型，經求解得到軸和葉輪裝配體的最大接觸壓力和平均接觸壓力的變化情況。

由圖10可知，最大接觸壓力隨軸彎曲程度的增大而增大，加熱時最大接觸壓力會減小，這是由于加熱降低了實際過盈量。

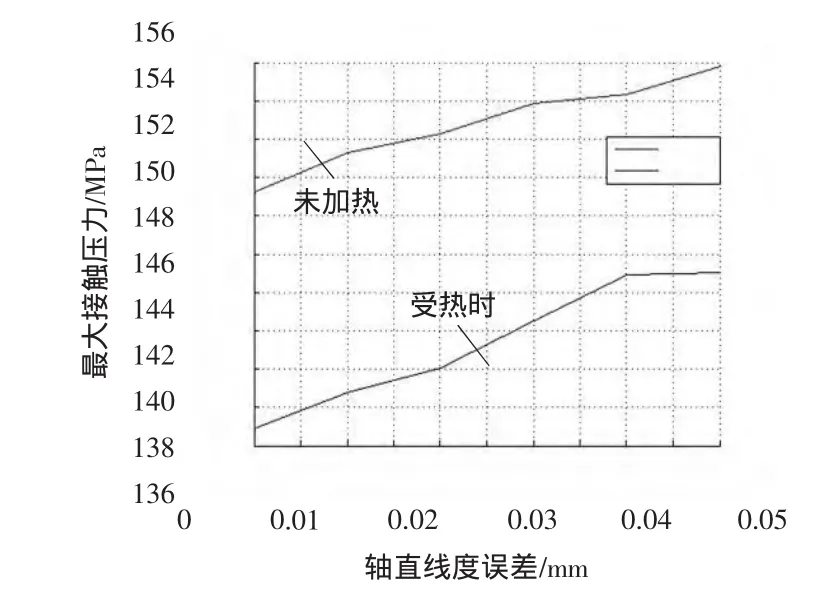
圖10 軸直線度誤差與最大接觸壓力的關系

由圖11可知，兩表面之間的平均接觸壓力隨軸的直線度誤差的增大變化很小。這是由于軸雖然存在直線度誤差，導致各處的接觸壓力分布發生變化，造成局部接觸壓力增大，但其他區域的接觸壓力會減小，而總的接觸壓力不會有較大的變化，因此使平均接觸壓力和拆解力不會隨誤差增大發生較大變化。這里也有可能研究的直線度誤差過小，且網格尺寸較大，導致平均接觸壓力變化不明顯。通過計算，得到軸和葉輪配合未加熱時，平均接觸壓力為115 MPa左右。加熱時降低到55 MPa左右。加熱時平均接觸壓力降低了約52%，因此拆解力也有相同的降幅。

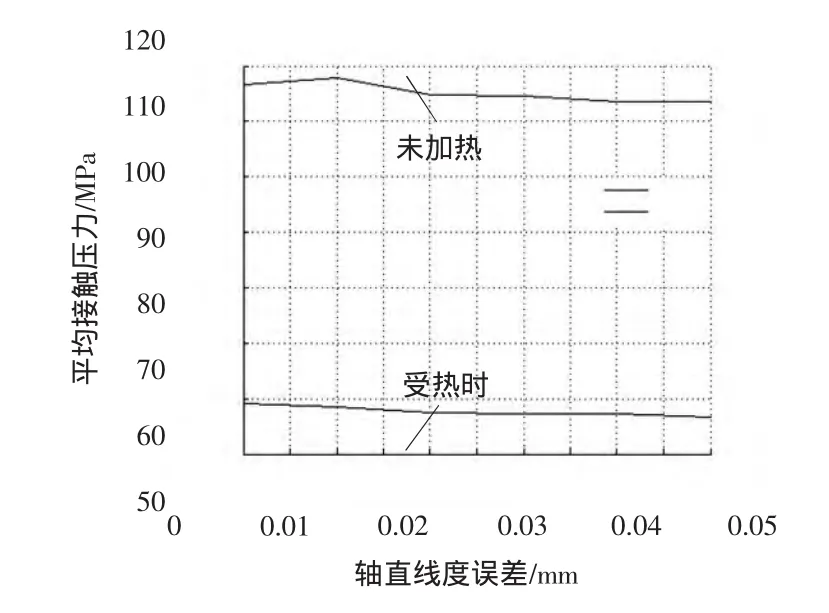
圖11 軸直線度誤差與平均接觸壓力的關系

3 結論

1）使用有限單元法求得了過盈配合的平均接觸壓力。

2）軸存在直線度誤差時，對過盈配合件的兩接觸表面的接觸壓力分布會有較大的影響。最大接觸壓力隨著軸直線度誤差增大而增大，平均接觸壓力和拆解力變化不大。

3）對葉輪加熱時，過盈配合的平均接觸壓力會有大幅度的降低，采用有限元方法求得變化規律。

［1］ 高俊福.大型離心壓縮機軸熱裝彎曲機理研究［D］ .大連：大連理工大學，2013.

［2］ 高耀東，張玉寶.ANSYS機械工程應用精華60例［M］.北京：電子工業出版社，2012.

［3］ Bengeri M,Mack W.Theinfluenceof thetemperaturedependence of the yield stress on the stress distribution in a thermally assembled elastic-plastic shrink fit［J］.ACTA MECHANICA,1994，103（1-4）：243-257.

［4］ 濮良貴，紀名剛.機械設計［M］.8版.北京：高等教育出版社,2005.

［5］ 李桂華.復雜規則曲面機械零件的熱變形理論及應用研究［D］.合肥：合肥工業大學，2006.