改進的BP神經網絡在刀具磨損狀態監測中的應用

何棟磊， 黃民

（北京信息科技大學 機電工程學院，北京 100192）

0 引言

作為前饋神經網絡的核心，BP神經網絡是目前應用最廣的一種人工神經網絡，其具有非線性映射、自適應、自學習和并行處理等特點。自從1987年Dornfeld和Ranguala［1］將BP神經網絡聯合多傳感器技術用于刀具磨損狀態監測，BP神經網絡在此領域內一直被廣泛而深入地研究，主要用于計算刀具磨損量并對刀具磨損狀態進行分類。但傳統的BP算法效率低，收斂速度較慢，容易陷入局部極小點，因此人們提出了許多改進方法，目的都在于提高收斂速度并改善易陷入局部極小的缺陷。

1 監測方法的選擇

目前，刀具磨損在線監測的常用方法主要有切削力監測、振動加速度監測、聲發射監測、電流和功率監測等。本文依據多傳感器融合技術，選擇振動傳感器和聲發射傳感器采集切削過程中刀具的動態信號，監測刀具的磨損狀態。振動信號是一種對刀具磨損及破損非常敏感的特征信號。在切削加工中，刀具與工件側面摩擦，不同磨損及破損程度的刀具，將會產生不同頻率結構的振動信號，包含與刀具狀態密切相關的豐富信息。根據加工方式的差別，需要選擇不同方向的振動信號監測刀具狀態。聲發射監測方法也是目前應用最廣泛且最具有潛力的一種方法。聲發射是一種物理現象，指固體材料在變形、破裂和相位改變時迅速釋放應變能而產生的一種彈性應力波［2］。通過聲發射傳感器測量切削過程中刀具產生的聲發射信號，適用于檢測刀具微小面積的破損和破損前產生的微裂紋。AE信號的頻率很高，一般在50 kHz以上，其能夠避開切削加工中振動和噪聲污染嚴重的低頻段，具有靈敏度高、信息量豐富等優點。

2 特征信號的分析及提取

刀具磨損狀態監測的關鍵是提取出與刀具磨損狀態密切相關的特征量。傳感器信號中除了有刀具磨損狀態信號，還包含噪聲及加工參數引起的干擾信號，不能直接用來監測刀具磨損，必須進行特征分析和選擇。由于切削加工中產生的信號包含了大量非平穩信號，且夾帶著瞬時突變成分，從時域上很難反映信號特征，從頻域上分析缺乏時域信息。因此，本文主要采用小波分析分解振動信號和AE信號，提取信號不同頻段的小波系數的均方根，建立與刀具磨損量之間的關系。另外，本文依據相關系數法對提取特征量進行優選，從而獲得最優的特征向量組輸入BP神經網絡。

3 BP神經網絡的改進研究

隨著對BP網絡的研究，BP網絡的局限性在實際應用中日益凸顯［3］，主要有：1）傳統 BP算法是一種梯度下降法，修正權值僅用到了誤差函數對權值的梯度,即一階導數信息，易導致學習過程發生振蕩，有可能陷入局部極小點。2）BP算法的學習效率η和動量因子α的很難確定。其中，η及α取值過大或過小都會對網絡的收斂速度和網絡穩定性產生巨大影響。3）網絡隱含層節點數和初始權值的確定隨機性和經驗性較大，沒有完整理論依據支持。由于Robert Hecht-Nielsen已經證明了可以用單隱含層的BP網絡去逼近任何一個閉區間內的連續函數，因此本文選擇帶單隱含層的三層神經網絡。

3 .1 改進BP算法

目前的改進算法主要有：附加動量法、學習速率可變法、彈性算法，變梯度法、擬牛頓法及L-M算法等。由于L-M算法收斂速度快且識別誤差小，因此本文選擇L-M算法。L-M算法是將梯度下降法和牛頓法相結合的算法［4］，使用了一階和二階導數信息。在開始時，梯度下降法下降較快，但接近最優值時下降變慢，轉向牛頓法可以在最優值附近產生更好的搜索方向。算法原理為

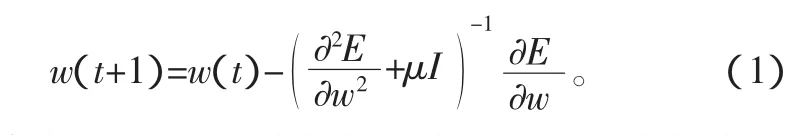
式中：I為單位矩陣；μ=0時為牛頓法，μ→∞時為梯度下降法。

3.2 改進樣本數據的歸一化方法

由于每個輸入樣本的物理量各不相同，為了消除物理單位的干擾，需要對樣本數據進行歸一化處理。通常以S形函數為激活函數的神經網絡將各輸入樣本歸一到［0，1］區間。本文為了使樣本數據更加緊湊，擴大網絡輸出空間，將樣本數據歸一化到［0.1，0.9］區間內。歸一化公式為

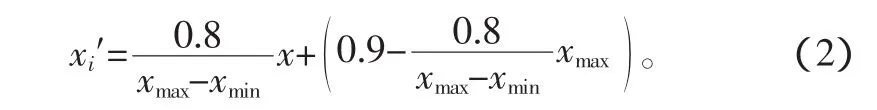
式中：xmax、xmin分別是該特征值歸一化前最大值和最小值；xi、xi′分別是歸一化前的值和歸一化后的值。

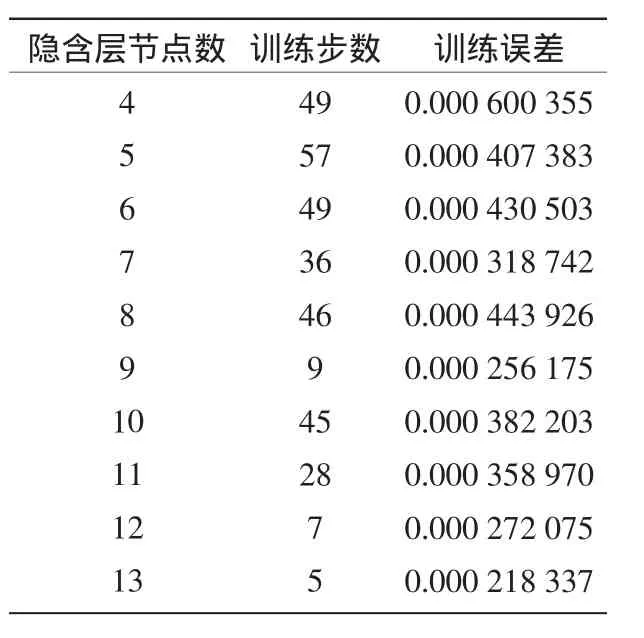
表1 不同隱含層節點數的訓練結果

3.3 優化選擇隱含層節點數

隱含層節點數的確定是個十分復雜的問題，對神經網絡的訓練精度和收斂速度有一定影響。隱含層節點數過少，降低樣本識別能力，容錯性差；節點數過多又會延長網絡訓練時間，泛化能力較差。往往憑借設計者的經驗來確定。為了減小盲目性，可參照以下公式：

式中：l為隱含層節點數；n為輸入節點數；m為輸出節點數；a為1～10的調節常數。

輸入同一個訓練樣本，只改變從所有網絡結構中選擇誤差最小時對應的隱含層節點數。通過MATLAB神經網絡［5］仿真實驗，不同隱含層節點數的訓練步數及誤差如表1所示。從表中可以看出，當隱含層節點數為13時訓練步數最少且訓練誤差最小，符合目標誤差，因此確定神經網絡的隱含層的節點數為13時最理想。

4 刀具磨損狀態監測實例

4.1 實驗設備

機床：DL-20MH數控車削中心，三軸聯動半閉環控制系統，主機由FANUC-0iTC系統控制，可對各種回轉體零件進行車削、鉆削、銑削加工。工件：45鋼，尺寸為φ90×380 mm。刀具材料：YT-15硬質合金刀具。加工方式：車削，加切削液。粗糙儀：上海某公司生產的TR240表面粗糙儀。振動監測設備：壓電式ICP：INV98822A加速度傳感器，共有4個，其中電主軸軸承位置的水平和垂直方向各安裝1個，刀柄及刀架位置各安裝1個；24位AD INV3018C采集卡，采樣頻率為5 kHz；DASP-10智能信號采集及分析系統。聲發射監測設備：R15A型聲發射傳感器，在刀柄及刀架位置各安裝1個；美國物理聲學公司的PCI-2型雙通道聲發射監測儀器。傳感器安裝位置如圖2所示。

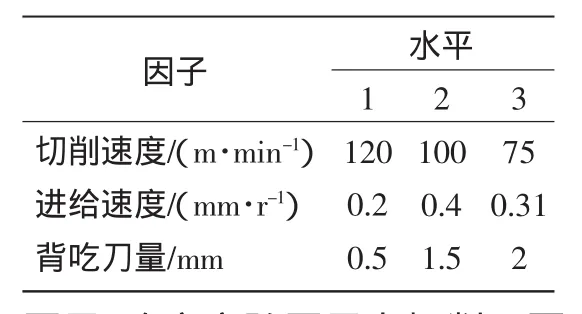
表2 實驗因子水平表

4.2 實驗方案

在刀具切削過程中，影響傳感器信號變化的因素很多，本實驗通過預處理和濾波等手段降低電氣和環境噪聲的干擾，剔除次要因子，確定實驗因子為切削三要素，即一個三因子三水平組成的實驗，如表2所示。設計正交實驗方案，共進行9組刀具磨損實驗。每組切削條件下，取刀具磨損量分別為0、0.1、0.3、0.5 mm 的刀片實驗，共進行 36 次實驗，將實驗數據作為BP神經網絡的訓練樣本，建立刀具磨損的監測模型。

實驗中選擇db4小波分別對3個刀具磨損程度不同階段對應的振動信號和聲發射信號進行4層小波分解，則每組信號的頻域被分解為8個頻帶，然后計算8個特征頻帶的小波系數的均方根值。利用相關系數法對特征量優化選擇后，本文選取振動信號和聲發射信號各3個特征頻帶的小波系數的均方根，再加上振動信號和聲發射信號的均方根值，共8個特征向量輸入BP神經網絡。文本最終確定的網絡結構為8-13-1，輸入層為8個神經元，當隱含層節點數為13時網絡誤差最小，輸出層為1個神經元，即代表刀具后刀面的磨損量VB，根據磨損量的不同，對應不同的磨損程度為：0～0.1 mm（初期磨損）；0.1～0.5 mm（中度磨損）；＞0.5 mm（嚴重磨損）。

4.3 實驗結果

根據上述建立的神經網絡模型，輸入層到隱含層的激活函數為Sigmoid函數，隱含層到輸出層的激活函數為purelin線性函數，初始化網絡權值系數在［0，1］之間，學習率取為0.01，學習誤差為0.0003，最大訓練次數為5000。基于不同算法的BP神經網絡的識別結果如表3所示。基于L-M算法的神經網絡最大識別誤差為0.025mm，而傳統BP算法的神經網絡最大識別誤差為0.136 mm，即基于L-M算法的神經網絡識別正確率明顯提高，能更好地滿足刀具磨損監測分類精度要求。

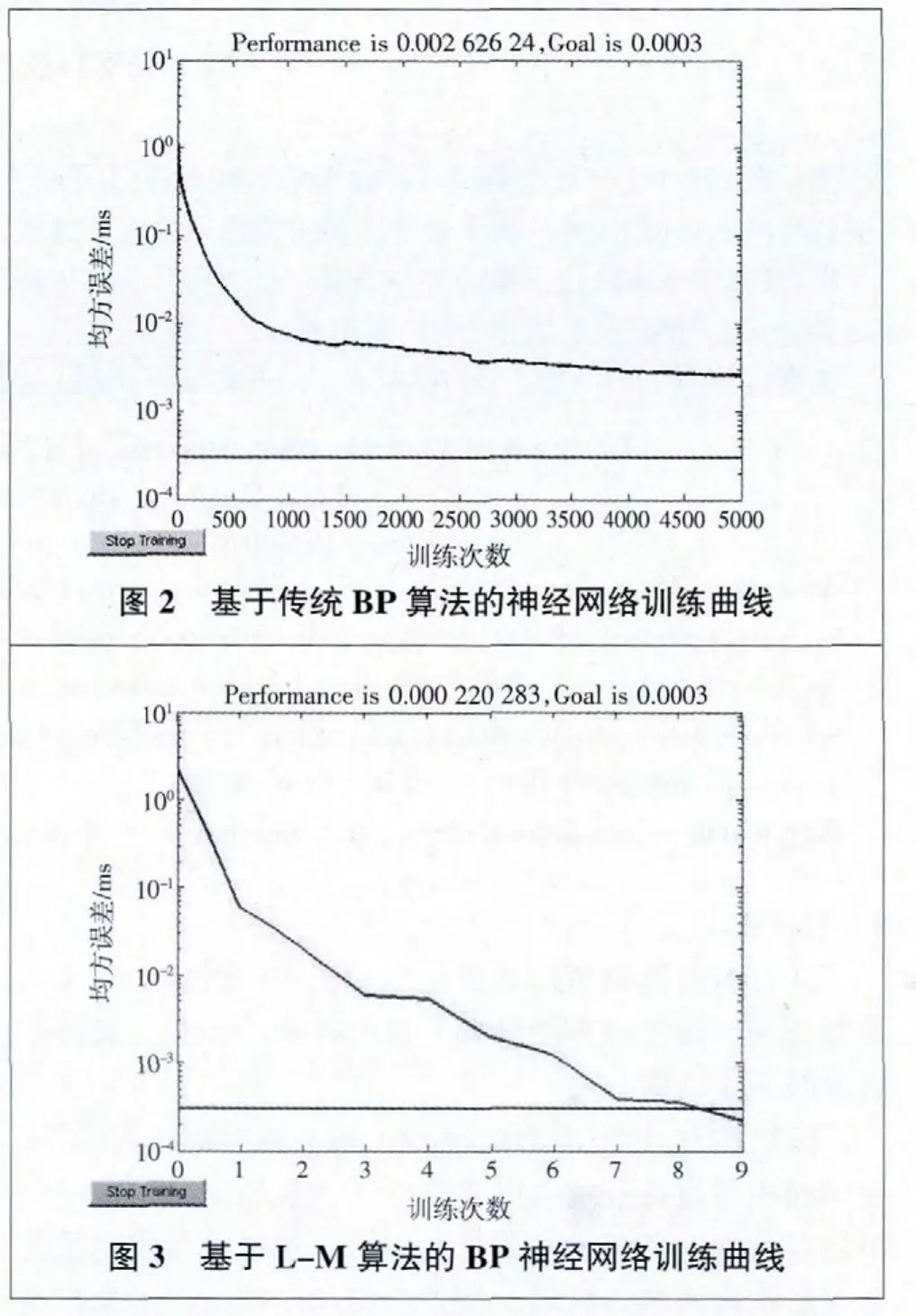
L-M算法和BP算法的神經網絡的收斂性能比較結果如圖3、圖4所示，在某一組切削條件下，前者訓練步數經過8步后即達到目標誤差，而后者經過5000步訓練后仍沒有達到目標誤差

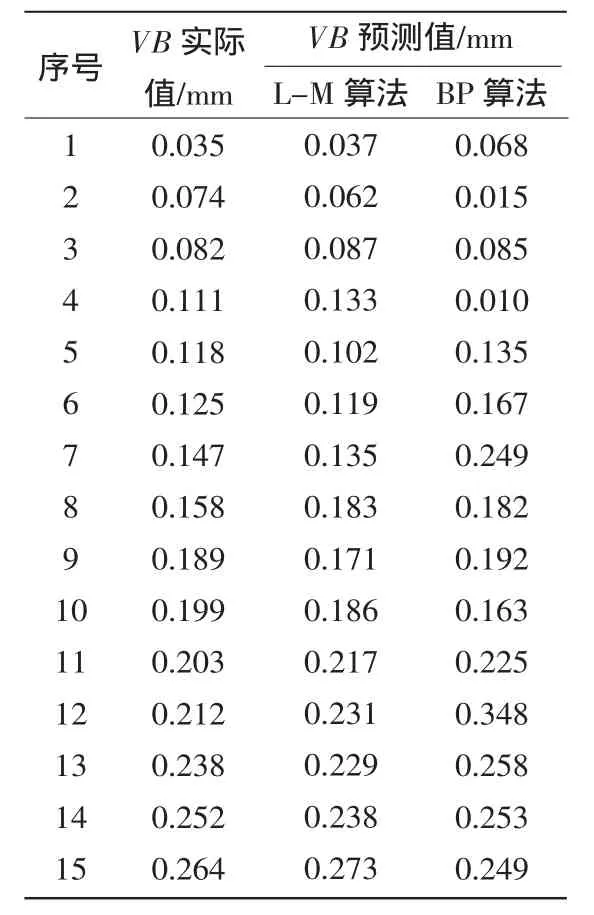
表3 L-M算法和BP算法的神經網絡識別結果

5 結 語

本文采用新的算法并合理調整網絡結構參數，明顯提高了網絡的收斂速度，獲得更好的識別精度，因此改進的BP神經網絡更適合于對刀具磨損狀態進行識別。

［1］ Dornfeld D A，盧冶.神經元網絡傳感器信息綜合用于刀具狀態監測［J］.組合機床與自動化加工技術，1991（7）∶35-41，50.

［2］ 黃民，劉秀麗，謝厚正.高檔數控機床刀具磨損故障監測方法及實驗系統［J］.北京信息科技大學學報(自然科學版)，2012（1）∶16-21.

［3］ 姜立芳，劉泊，施蓮輝.一種改進的BP算法及其在模式識別中的應用［J］.哈爾濱理工大學學報，2003（3）∶90-92，95.

［4］ 關山，聶鵬.L-M優化算法BP網絡在刀具磨損量預測中的應用［J］.機床與液壓，2012，40（15）∶22-26.

［5］ 傅薈璇，趙紅.MATLAB神經網絡應用設計［M］.北京：機械工業出版社，2010：83-100.