快速檢驗梅森素數的一種新方法

林柏鋼

(1. 福州大學數學與計算機科學學院，福建 福州 350116；2. 網絡系統信息安全福建省高校重點實驗室，福建 福州 350116)

快速檢驗梅森素數的一種新方法

林柏鋼1,2

(1. 福州大學數學與計算機科學學院，福建 福州 350116；2. 網絡系統信息安全福建省高校重點實驗室，福建 福州 350116)

研究梅森素數與偶完全數的內在聯系，分析偶完全數因子分解的結構特點，分別得到一個準偶完全數序列的通項公式：Sn=22n-2·(22n-1-1)，和一個準梅森素數序列的通項公式：SMn=(22n-1-1). 最后給出快速檢驗梅森素數新方法的算法思路.

準偶完全數序列； 通項公式； 梅森素數； 快速檢驗算法

0 引言

公鑰密碼的特點之一就是與素數緊密相關，判定素數、大數分解以及尋找最大的素數，始終是人們關注的課題[1-2]. 在我們所知道的梅森素數尋找過程中，如果說至今為止已找到的第48個梅森素數(對應確定的第48個偶完全數)，那可是花了九牛二虎之力才取得的成果[3-4]. 也就是說，從尋找第35個梅森素數開始，靠的是現代互聯網技術才得以取得突破進展. 20世紀90年代中后期，在美國程序設計師沃特曼和庫爾沃斯基等人的共同努力下，成立了世界上第一個基于互聯網的分布式計算項目——因特網梅森素數大搜尋(GIMPS)計劃[5-6]. 人們只要在GIMPS的主頁上下載一個計算梅森素數的免費程序，就可以立即參加該項目來搜尋新的梅森素數. 1996年11月13日，Joel Armengaud基于GIMPS平臺，找到了第35位梅森素數，對應p=1 398 269，Mp= 814 717 564…451 315 711，素數有420 921位. 2013年1月25日，美國中央密蘇里大學柯蒂斯·庫珀(Curtis Cooper)教授的研究小組發現了最大的素數Mp=257 885 161-1=58 188 726 623 224 644 217…46 141 988 071 724 285 951，是第48個梅森素數，對應p=57 885 161，該素數有17 425 170位. 由此可見尋找和發現更大梅森素數是多么的艱難.

盡管尋找梅森素數困難重重，但人們還是想盡各種辦法解決[7-8]，包括梅森素數和偶完全數的研究歷來備受人們關注，因為偶完全數的存在總是伴隨和依賴著梅森素數的發現而確定，兩者之間不是孿生兄弟關系，而是連體嬰兒關系. 只要發現一個新梅森素數，偶完全數就是它的副產品. 本文從研究偶完全數的分布特征入手，研究偶完全數的因子展開存在規律，進而確定對應的梅森素數的存在，并給出梅森素數的定位內在聯系，最后給出判定梅森素數的新方法.

1 梅森素數與偶完全數的內在聯系

定義1 幾個符號約定：Mp表示由正整數p所形成的梅森素數，記為Mp=2p-1；Ep表示由正整數p所形成的偶完全數，記為EP=2p-1·(2p-1)；φEp表示偶完全數的因子分解總項數;KEp表示分解因子成鏡像對稱兩兩相乘等于自身偶完全數的本數數目.

定義2 稱準偶完全數序列(sequenceofpseudo-evenperfectnumber,SPEPN)是指除偶完全數6外，序列形如： 1,28*,496*,8 128*,130 816,2 096 128,33 550 336*,536 854 528,8 589 869 056*,137 438 691 328*，… . 其中帶星號的整數為大于6的偶完全數.

定義3 稱偶完全數序列(sequenceofevenperfectnumber,SEPN)是指包含偶完全數6在內的可能存在都是偶完全數的序列. 即： 6*，28*,496*,8 128*,33 550 336*,8 589 869 056*,137 438 691 328*，….

根據偶完全數的定義： 若p與(2p-1)為素數，則2p-1.(2p-1)為偶完全數. 同理，根據梅森素數定義，也只有當(2p-1)為素數時才稱為梅森素數. 由Ep的相關性質特點，我們知道: ① 偶完全數的構造滿足公式EP=2p-1·(2p-1)； ② 偶完全數的表達結果具有2p-1～22p-2范圍的連續方冪之和； ③ 偶完全數的展開表達式呈三角形排列，等等.

由偶完全數性質不難得到：

定理1 準偶完全數序列的通項公式為：

Spepn=22n-2·(22n-1-1) (n≥1)

證明 根據偶完全數的性質②，準偶完全數序列的每個數也可以按一定范圍的連續方冪之和展開排列，具體如下(其中n≥1為順序號)：

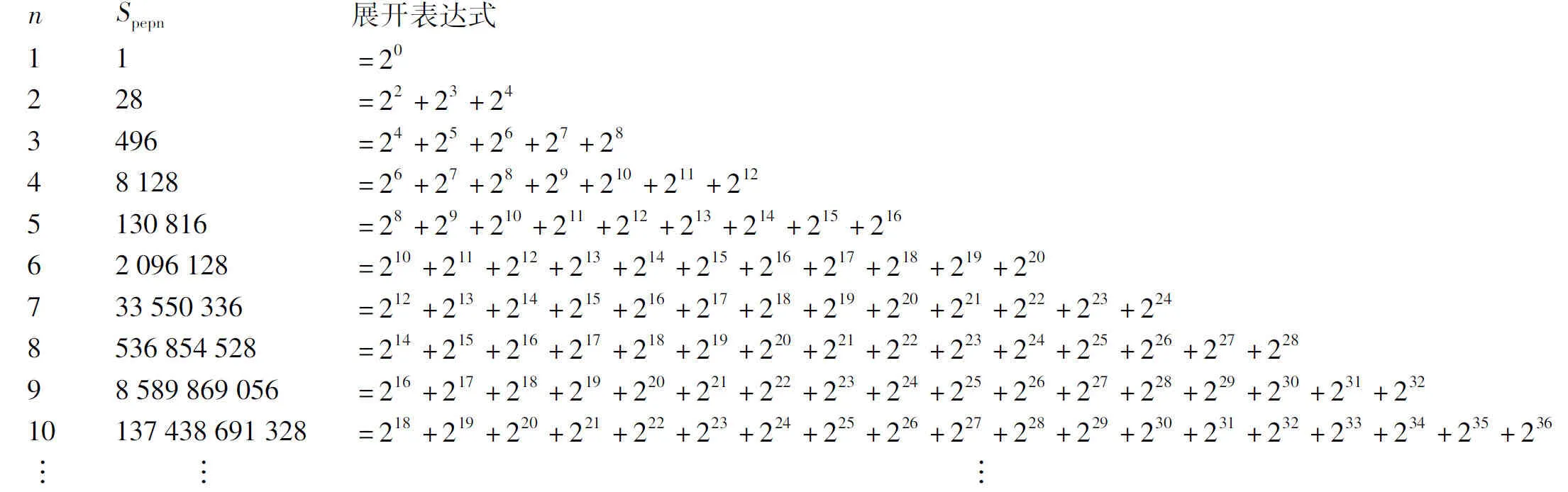
根據上述展開表達式，不失一般性可以給出基本表達式：

an=22n-2+2(2n-2)+1+2(2n-2)+2+…+2(2n-2)+(2n-4)+2(2n-2)+(2n-3)+2(2n-2)+(2n-2)

定理2 除偶完全數6外，偶完全數的序列SEPN是準偶完全數序列SPEPN的特列.

證明 由偶完全數的構造公式： (2p-1)·(2p-1)可知： 令p=2n-1，則有

根據偶完全數性質②可知，偶完全數具有2p-1～22p-2范圍的連續方冪之和. 考慮p?2n-1,當p=2n-1時，而準偶完全數序列SPEPN具有22n-2～24(n-1)范圍的連續方冪之和. 除偶完全數6外，兩者方冪個數均為奇數.

又因為連續方冪之和： 2p-1～22p-2? 22n-2～24(n-1)，所以定理2得證.

推論1 任一偶完全數Ep一定存在準偶完全數序列SPEPN中.

證明 由定理2易得本推論成立.

定理3 偶完全數的因子分解項排列結構為： 首項k0=20=1，k1項之后各因子按2n規律升冪展開，典型中項因子(包括左右兩項)分別為：kml=22(n-1)，kmr=(2(2n-1)-1)； 之后各因子按對稱鏡像映射遞減2n規律分布，尾項kend=24(n-1)-22n-3.

證明 根據偶完全數的因子展開分布，其各因子排列結構形式如下(其中p為素數)：

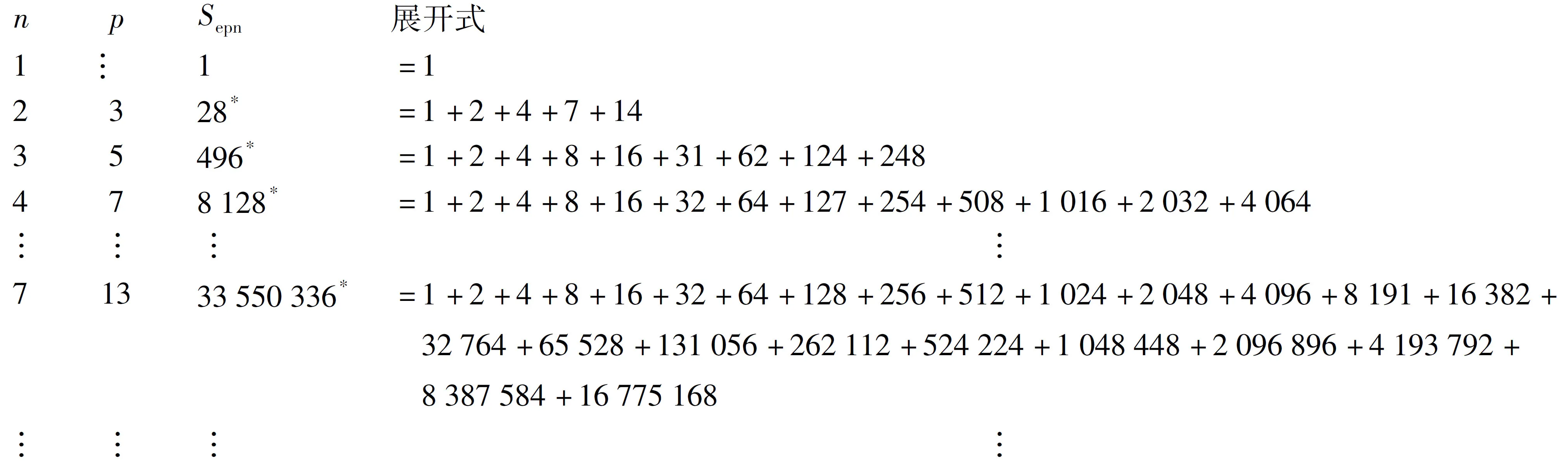
由偶完全數的因子展開式知道，它的一般表達式為：

令p=2n-1時，則有：

展開結果就有首項k0=20=1，前半部分大括弧中k1項之后按2n規律展開，中括弧中典型中項(包括左右兩項)分別為：kml=22(n-1)，kmr=(2(2n-1)-1)； 后半部分大括弧中各因子則按對稱鏡像映射遞減2n規律分布，結果就有尾項kend=24n-4-22n-3=24(n-1)-22n-3.

定理4 偶完全數的因子分解項恒為奇數，總項數φEp=4n-3； 滿足偶完全數自身數項目數為KEp=2(n-1).

證明 因為偶完全數的因子分解特點是首項必為20=1，其余分解因子成鏡像對稱兩兩相乘等于各偶完全數，結果必為偶數，加上首項總項數恒為奇數. 另由偶完全數的因子展開式可以看出，n=1，φEp(1)=1；n=2，φEp(28)=5；n=3，φEp(496)=9； …； 以此類推，當n≥1時，每個偶完全數的因子分解總項數恒為φEp=4n-3.

另證KEp，因為分解因子首項恒為1，其余分解因子成鏡像對稱兩兩相乘等于自身偶完全數，故有本數數目KEp=[(4n-3)-1]/2=2(n-1).

定理5 在偶完全數的因子分解總項數中，第2n項位置一定是梅森素數： (2p-1).

證明 根據定理4和偶完全數分解特點可知，除首項Ep(1)=1外，其余各項因子成鏡像對稱兩兩相乘等于給定偶完全數本數. 因此有(4n-3)-1=4(n-1)個因子構成兩兩相乘等于給定偶完全數本數，且KEp=2(n-1). 在所有這樣本數鏡像相乘組合對存在中，唯有中間左右兩項展開式因子能夠滿足鏡像相乘結果，符合2p-1×(2p-1)=Ep條件，即：

{Ep(2n-1)=22(n-1),Ep(2n)=22n-1-1} ? {(22(n-1)×(22n-1-1))=Ep}

當p=2n-1時，則有下式成立：

{Ep(2n-1)=2p-1,Ep(2n)=2p-1}? {(2p-1×(2p-1))=Ep}

其余各項鏡像相乘結果雖然也滿足偶完全數的本數存在，但不符合偶完全數條件. 另根據偶完全數定義，若Ep為偶完全數，則p與(2p-1 )必定為素數. 反之，若p為素數，(2p-1)為非素數，則偶完全數不成立. 又因為Ep中的(2p-1)項加上首項，剛好落在分解展開式(2n-1)+1=2n項位置，故可確定第2n項位置一定是梅森素數： (2p-1).

推論2 任一梅森素數也一定存在準偶完全數序列SPEPN中.

證明 由偶完全數和梅森素數的關系，以及定理5易證本推論成立.

引理1 當n≥1時，序列：bn=20+21+22+23+…+22n-3+22n-2的前(2n-1)項和為：

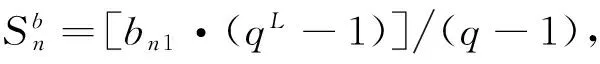
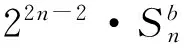
證明 根據準偶完全數特點，還可將其各因子展開如下形式排列(其中p為素數，*表示偶完全數)：

npSpepn展開形式1?120·(20)2328*22·(20+21+22)35496*24·(20+21+22+23+24)478128*26·(20+21+22+23+24+25+26)5?13081628·(20+21+22+23+24+25+26+27+28)????

由展開式可知，對應每個n，展開式的左邊恒為22n-2，右邊括弧中的序列形式為：

bn=20+21+22+23+…+22n-3+22n-2

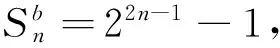
定義4 形如： 1,7*,31*,127*,511，2 047，8 191*，32 767，131 071*，524 287*，2 097 151，8 388 607，33 554 431，134 217 727，536 870 911，2 147 483 647*，…，稱為準梅森素數序列，記為SMn，(其中除3外，帶*號數全為梅森素數).

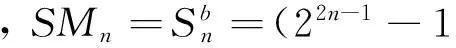
證明 當n≥1時，序列Mn中的每個數展開形式均為： 20+21+22+23+…+22n-3+22n-2

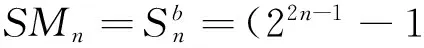
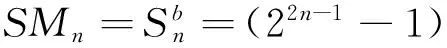
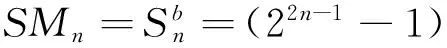
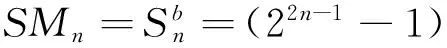
證明 由展開式易證推論3成立.

定理9 (ⅰ)若(22n-1-1)為已知數，則(2n-1)=log2(22n-1)；

(ⅱ)若2n-1=p，則有p=log2(22n-1).

證明 (ⅰ)已知(22n-1-1)數值給定，根據對數公式，則有下式成立：

(2n-1)=log2[(22n-1-1)+1]=log2(22n-1)

(ⅱ)同理，若令2n-1=p，由(ⅰ)可證(ⅱ)成立.

2 梅森素數的快速判定算法思路

算法1 根據準偶完全數序列SPEPN，檢驗梅森素數.

1) 從準偶完全數序列SPEPN中確定偶完全數Ep；

2) 由偶完全數Ep的展開形式，判定梅森素數存在.

算法2 根據準梅森素數序列SMn，檢驗梅森素數存在.

算例分析 根據算法1檢驗梅森素數存在. 由準偶完全數序列SPEPN中檢驗n=10時，Spepn=137 438 691 328的數確信是梅森素數的結果.

1) 從準偶完全數序列SPEPN中確定偶完全數Ep.根據定理3分解規則，從第1項開始到2n-1項之前，按2n升冪展開(簡單算法就是： 從第2項開始，2×前項到(2n-1)項為止)，2n項之后到結束項kend=24(n-1)-22n-3為止，偶完全數Ep對應分解各項按對稱映射遞減2n規律展開(簡單算法就是： 從(2n+1)項開始，2×前項到結束項(kend=24(n-1)-22n-3)為止). 檢驗判定若Ep確定為偶完全數，最后可得到n=10時，偶完全數Ep=137 438 691 328的展開形式為：

2) 由偶完全數Ep的展開式，判定梅森素數存在. 根據定理5，處于展開式中第2n=20項位置一定是梅森素數：Mp=2p-1= 524 287. 另據定理9(ⅱ)，其對應素數p=log2(22n-1)=log2(22×10-1)=19.

必須指出，對于p為素數，但不是梅森素數情形時，檢驗是否為偶完全數Ep也很簡便，只要找到一個因子不滿足偶完全數要求計算就停止. 這里不再贅述.

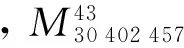
3 結語

在網絡安全日益突出的今天，在GIMPS計劃平臺上尋找更大的梅森素數，不僅反映計算機網絡硬件的數據處理能力，同時也是綜合各種計算方法的準確運用和水平的真實體現，它對基礎數論研究，對計算機學科發展，尤其對密碼學領域的大數分解和安全素數聯系緊密的應用方面有著極其深刻的影響. 本文通過分析梅森素數和偶完全數的相關內在聯系，從中找出偶完全數的基本展開規律，給出了準偶完全數序列SPEPN的通項公式和準梅森素數序列SMn的公式，最后給出快速檢驗梅森素數新方法的算法思路，無疑對快速尋找更大的梅森素數是一個新的研究途徑.

[1] 蓋伊RK.數論中未解決的問題[M].2版.張明堯，譯.北京： 科學出版社，2003: 12-17.

[2]CrandallR，PomeranceC.Primenumbers:acomputationalperspective[M]. 2nded.NewYork：Springer，2005.

[3]Knowprimes:listofknownMersenneprimenumbers[EB/OL]. [2015-07-08].http://www.mersenne.org/primes/greatInternetMersenneprimesearchGIMPS/current progress/

[4] 周海中.梅森素數的分布規律[J].中山大學學報:自然科學版，1992，31(4)，121-122.

[5] Website. PrimeNet CPU benchmarks (GIMPS)[EB/OL]. (2014-01-01)[2015-07-08].http://www.mersenne.org/report_benchmarks/get started/CPU benchmarks.

[6] 高全泉.大互聯網梅森素數尋求(GIMPS)研究計劃進展[J]. 數學的實踐與認識，2006，36 (1)： 232 -238.

[7] Thall A. Fast Mersenne prime testing on the GPU[EB/OL]. (2011-05)[2015-07].http:// www.researchgate.net/

[8] 張四保.關于完全數的研究[D].成都： 成都理工大學，2008.

(責任編輯： 鄭美鶯)

A new method of quick test Mersenne prime

LIN Bogang1,2

(1. College of Mathematics and Computer Science,Fuzhou University,Fuzhou,Fujian 350116,China;2. Key Lab of Information Security of Network System in Fujian Province,Fuzhou,Fujian 350116,China)

The relation about Mersenne prime and even perfect number is researched,the structure feature of factorization for even perfect number is analysis. The study obtain two important result: a general formula of sequence of pseudo-even perfect number (SPEPN) isSn=22n-2·(22n-1-1),another general formula of sequence of pseudo-Mersenne prime (SPMP )isSMn=(22n-1-1). And a new method of quick test Mersenne prime is given.

sequence of pseudo-even perfect number; general formula; Mersenne prime; quick testing method

2015-08-20

林柏鋼(1953-)，教授，博導，主要從事網絡與信息安全、編碼與密碼、云計算與物聯網安全、可信計算等研究，linbg@fzu.edu.cn

國家自然科學基金資助項目(61402112)

10.7631/issn.1000-2243.2015.05.0577

1000-2243(2015)05-0577-05

O156

A