半嚴格凸函數的性質及應用
李艷
(延安職業技術學院,陜西延安716000)
半嚴格凸函數的性質及應用
李艷
(延安職業技術學院,陜西延安716000)
凸函數是一類重要的函數,它在凸分析和數學規劃等學科中扮演著主要的角色,在不等式證明方面及其它各領域有著廣泛的應用。本文在楊新民對半嚴格凸函數研究的基礎上,給出了半嚴格上凸函數和半嚴格下凸函數的一些性質,研究了它們在不等式證明中的應用,并給出了若干例子。
半嚴格凸函數;性質;不等式;應用
一、引言
凸函數是凸分析中研究的主要內容,它在數理經濟、工程、管理科學及優化理論中有廣泛應用,特別是在數學規劃的各個分支中經常涉及到凸函數。文獻[1-5]中給出了上(下)凸函數,嚴格上(下)凸函數的定義和性質。文獻[7-10]中給出了凸函數及嚴格凸函數在積分不等式中的應用。楊新民在文獻[6]中給出半嚴格凸函數的定義,并討論了凸函數、半嚴格凸函數和嚴格凸函數之間的關系。
本文對半嚴格凸函數作了進一步研究和討論。在預備知識中給出半嚴格上(下)凸函數的定義,在主要結果中給出半嚴格上(下)凸函數的一些性質,研究它們在不等式證明中的應用,并給出若干例子。這在一定意義上推廣和完善了半嚴格凸函數。
二、預備知識
定義1[1]設函數?(x)在區間[a,b]上連續,若對任意x1,x2∈[a,b],以及任意λ∈(0,1),有
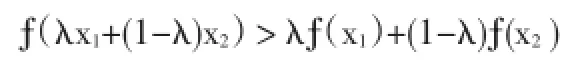
則稱?(x)為[a,b]上的凸函數.
定義2[1]設函數?(x)在區間[a,b]上連續,若對任意x1,x2∈[a,b],以及任意λ∈(0,1),有
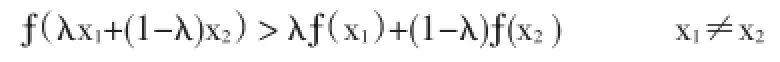
則稱為[a,b]上的嚴格凸函數.
定義3[1]設函數?(x)在區間[a,b]上連續,若對任意x1,x2∈[a,b],以及任意λ∈(0,1),有
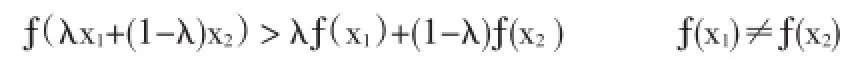
則稱?(x)為[a,b]上的半嚴格凸函數.
注:定義1[1[1]中不等式符號反向,則稱?(x)為[a,b]上的半嚴格上凸函數。在下文中我們主要討論半嚴格上凸函數和半嚴格下凸函數的性質及應用。
三、主要結果
現在我們提出半嚴格上凸函數和半嚴格下凸函數的一些性質。
定理1設?(x)在區間[a,b]上的半嚴格上凸函數,則對于任意的a∈[0,1](或a∈[-1,0])有,a?(x)在[a,b]上是半嚴格上(下)凸函數.
直接由定義可證.
定理2設?(x),g(x)在區間[a,b]上是半嚴格上凸函數,則?(x)+g(x)在[a,b]上也是半嚴格上凸函數.
證明?(x),g(x)在區間[a,b]上是半嚴格上凸函數,對任意x1,x2∈[a,b]有
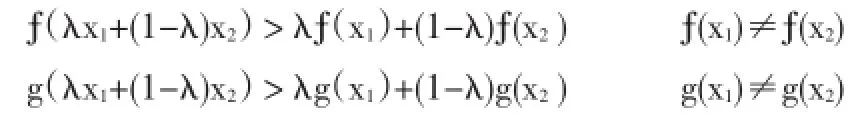
從而
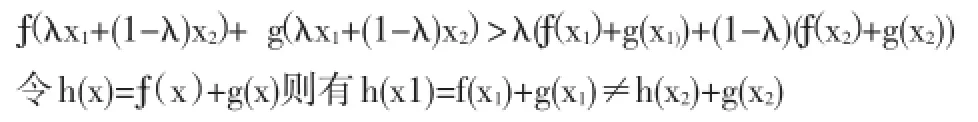
因此h(x)是半嚴格上凸函數,即?(x)+g(x)在[a,b]上是半嚴格上凸函數.
定理3 1。若?(u)是半嚴格上凸且單調增加的函數,g(x)是半嚴格上凸函數,則?(g(x))也是半嚴格上凸函數.
2。若?(u)是半嚴格下凸且單調減少的函數,g(x)是半嚴格上凸函數,則?(g(x))是半嚴格下凸函數.
3。若?(u)是半嚴格下凸且單調增加的函數,g(x)是半嚴格下凸函數,則?(g(x))是半嚴格下凸函數.
4。若?(u)是半嚴格上凸且單調減少的函數,g(x)是半嚴格下凸函數,則?(g(x))是半嚴格上凸函數.
證明1。g(x)是半嚴格上凸函數,則有
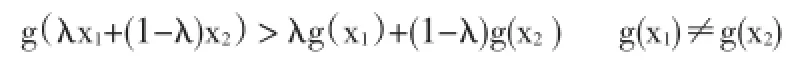
而?(u)是半嚴格上凸且單調增加的函數,因此
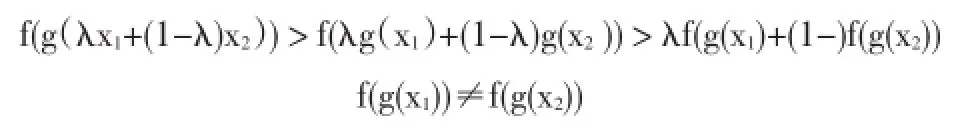
故?(g(x))是半嚴格上凸函數.
同理可證性質2。-4。.
由性質3。可得
1。若?(x)是半嚴格下凸函數,則e?(x)也是半嚴格下凸函數.
2。若?(x)是半嚴格上凸函數,則In?(x)也是半嚴格上凸函數.
進一步可得
esinx在[2kπ,2kπ+2π](k=0,±1,±2…)是半嚴格下凸函數;
Insinx在[2kπ,2kπ+2π](k=0,±1,±2…)上是半嚴格上凸函數.
定理4 1。設y=?(x)是半嚴格上凸且嚴格增加函數,則其反函數x=?-1(y)是半嚴格下凸嚴格增加函數.
2。設y=?(x)是半嚴格上凸且嚴格減少函數,則其反函數x=?-1(y)是半嚴格上凸嚴格減少函數.
3。設y=?(x)是半嚴格下凸且嚴格增加函數,則其反函數x=?-1(y)是半嚴格上凸嚴格增加函數.
4。設y=?(x)是半嚴格下凸且嚴格減少函數,則其反函數x=?-1(y)是半嚴格下凸嚴格減少函數.
證明1。y=?(x)是嚴格增加函數,則其反函數x=?-1(y)也是嚴格增加函數.由y=?(x)是半嚴格上凸函數,有
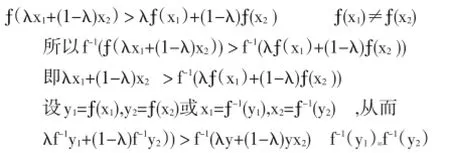
即?-1(y)是半嚴格下凸且嚴格增加的函數.
同理可證性質2。-4。.
下面我們給出半嚴格凸函數的一些應用.先介紹Jensen不等式然后考慮在證明積分不等式方面的應用.
例1(Jensen不等式)設?(x)為[a,b]上的半嚴格上凸函數.t1>0(i=1,2,…,n)且則
證明對n采用數學歸納法.
當n=2時,有
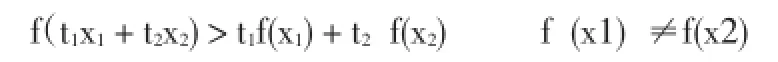
即為半嚴格上凸函數的定義.
設結論對于n≤k-1時成立,下面證明n=k時結論也成立.
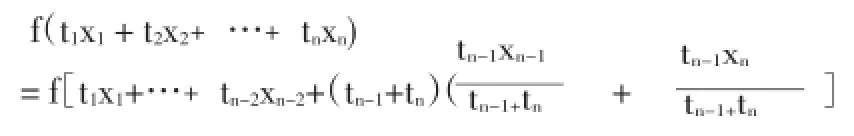
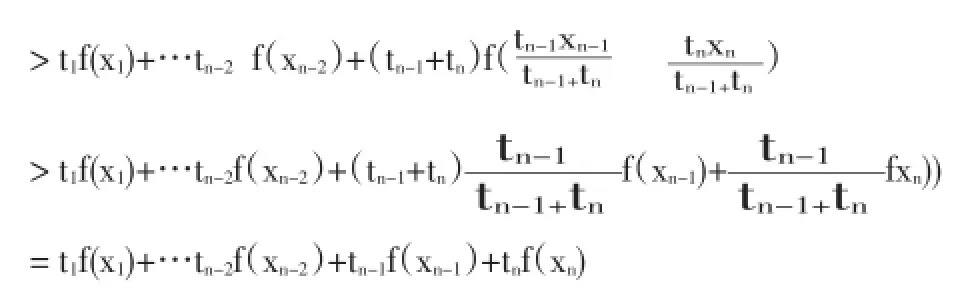
由數學歸納法知,結論成立.
例2設?(x),g(x)在區間[a,b]上可積,且m≤?(x)≤M,g(x)≥0,及∫bg(x)dx>0,R(t),R(t)在[m,M]上是半嚴格上凸函數,則
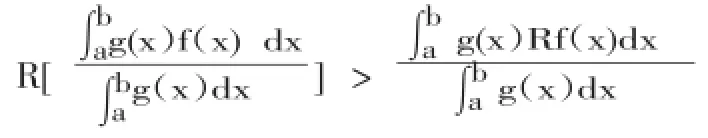
證明?(x),g(x)在區間[a,b]上可積,因此無論對[a,b]作怎樣的分割,其積分和的極限存在且相等.對[a,b]作n等分,并設
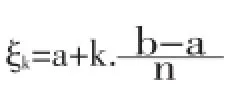
考慮到R(t)為半嚴格上凸函數及
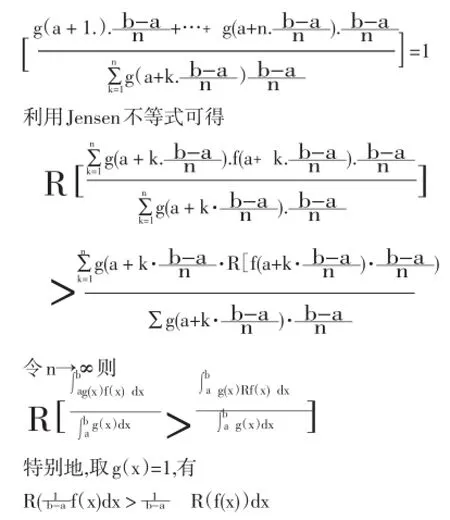
例3設?(x),g(x)是[a,b]上的正值連續函數,g(x)非常數,則
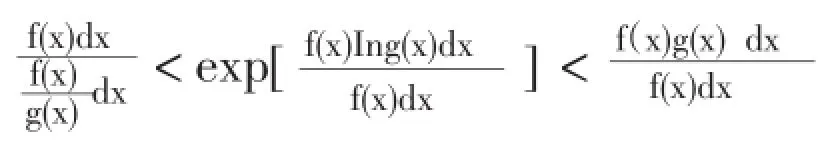
證明利用例2的結論.
1。設R(t)=-et,則R(t)是半嚴格上凸函數
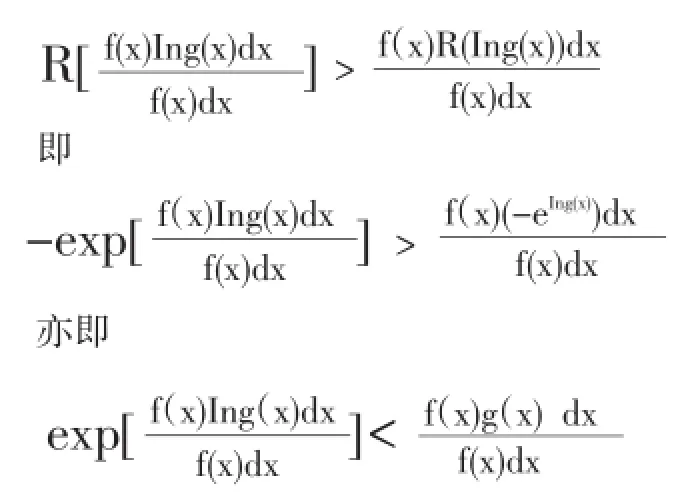
2。設Q(t)=-et,則Q(t)是半嚴格上凸函數.仿1。之證法,即可得
O174.13
A
1674-6198(2015)03-0076-03
2015-05-12
李艷(1986-)女,陜西佳縣人,延安職業技術學院教師。

