關于五行理論數學模型的參數反演

舒彬

（陜西學前師范學院，陜西 西安 710100）

在各個技術領域中，經常見到以待定未知參數這類反問題，要待定未知參數，最直接的方法是測量這些未知參數在一些離散點處的值，但似乎這類方法又行不通。此時只好通過測量微分方程組在若干點處的解的信息，來推算方程中的未知參數。對于參數估計的優化方法，其實是要在計算量和算法穩定性之間有一個權衡，而信賴域方法用較少的計算成本提高了算法的穩定性。信賴域法是一種比較復雜但很有效地優化算法，本文以信賴域算法為基礎，討論了五行理論數學模型的參數反演問題，最后給出了數值模擬。

1 問題的提出

金木水火土相生關系是木生火，火生土，土生金，金生水，水生木，就類似于大自然中，木燃燒為火，金屬產生于土中，金屬熔化則為水，水滋潤則木長，五者相生，金克木，火克金，水克火，土克水，木克土，互相聯系[1]。自然界萬事萬物都可取類比歸于這五個系統，這五大系統之間有生我，我生，克我，我克四種關系，因此構成了四種關系五個方面。這種生中有克，克中有生的觀點基本上反映了控制論中的輸入與輸出的作用。

如果用y1,y2,y3,y4,y5分別代表五行木，火，土，金，水，并從五行之間的相互生克關系可得到五行動力系統的微分方程組，如下[2,3]：

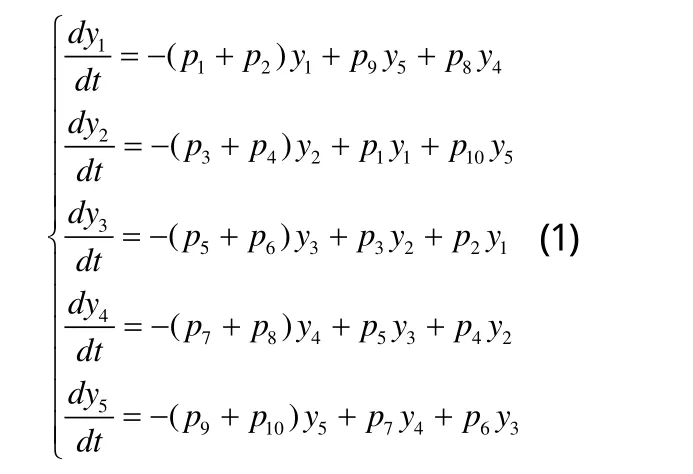
上式中，pi(i= 1 ,2,...,10)代表輸入輸出的速率，yi(i= 1 ,2,...,5)代表五行陰與陽的絕對值，t代表時間。在五行之間產生了陰陽的輸出流動，從而維持了生態間的陰陽平衡。pi(i= 1 ,2,...,10)通常未知，它們的確定有著重要的理論價值和實際意義[4]。

2 分析并實現算法步驟

將上述模型推廣到更為一般的數學模型，如下：

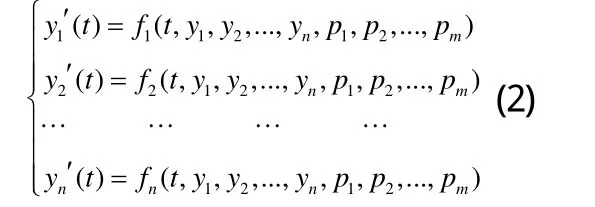
初始條件為：

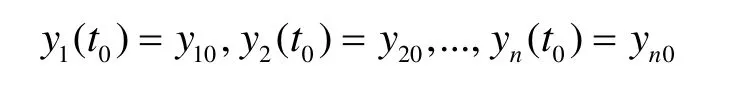
其中，p1,p2,...,pm是參數，表示為向量：

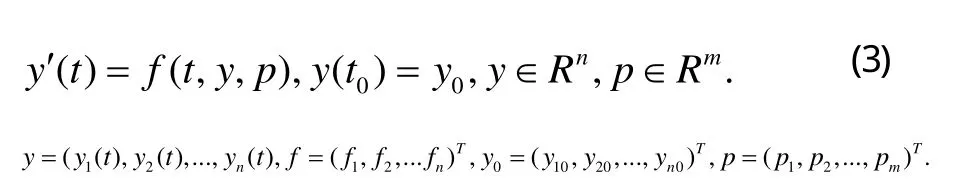
假設已知參數p1,p2,...,pm和初始條件，那么求解(3)則可知此方程的變化規律。在實際生產問題中，物體特性的參數用p1,p2,...,pm來表示，并且不可知，怎樣利用已知信息和上述方程組來確定未知的參數，即可構成參數識別的反演問題。

要反演參數p1,p2,...,pm，必須附加先驗條件，可取有限個時間點上的已知解，假設已知：y1(tl) ,y2(tl) ,...,yn(tl)，l= 1 ,2,...,r。但在實際問題中，數據的已知，難免有一定的誤差，從而實際應得數據是：

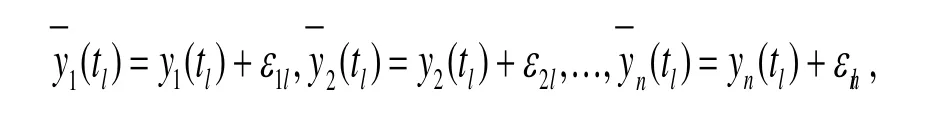
其中，ε1l,ε2l,… ,εnl為擾動量。

那么，參數反演可描述為求解以下的最小二乘優化問題：

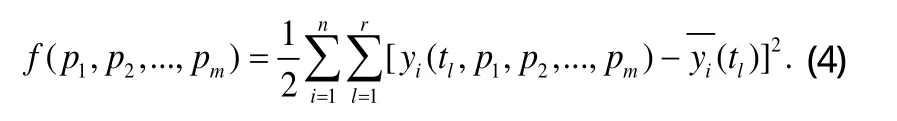
其中，yi(tl,p1,p2,...,pm)是以p1,p2,...,pm為參數解原問題(1)獲得的相應的計算值。

在信賴域內通過求解一個二次規劃取到可行點，即是信賴域算法的思想。在解(3)時，可行點 (p1(k),p2(k),...,pM(k))處，給出信賴域半徑rk下只需求解以下的子問題便可得出搜索方向：

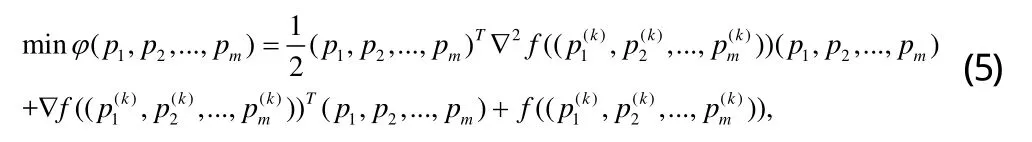
滿足

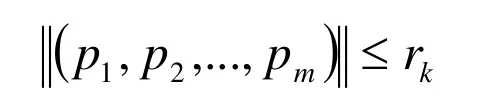
搜索方向得到后，修正信賴域半徑。

實現算法的過程：

步驟2 計算梯度

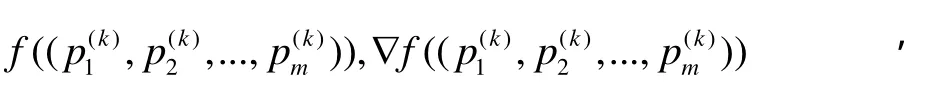
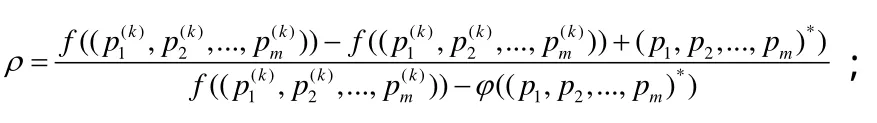
步驟4 如果ρ≤μ,令

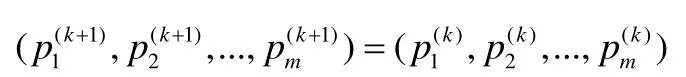
否則，

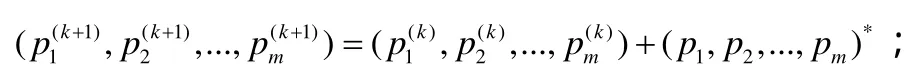
步驟5 按下式修改信賴域半徑：

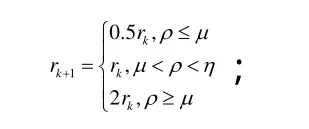
其中，μ= 0.25，η=0.75。

步驟6 置k=k+ 1 ,轉步驟2。

3 數值算例

3.1 參 數反演

模擬數值時，取初始條件

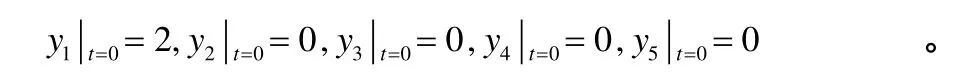
為了反演參數，需要附加一定的先驗條件，先給出p1,p2,p3,p4,p5,p6,p7,p8,p9,p10真值，取

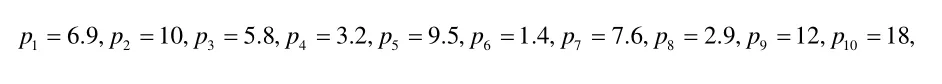
由數值計算得出y1,y2,y3,y4,y5在任意時刻t的數值解，并且把y1(t),y2(t),y3(t),y4(t),y5(t)在

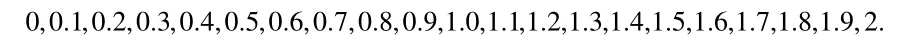
處的值加上一定擾動的δ＞0作為已知條件來反求參數。應用信賴域算法時，參數的初始取值

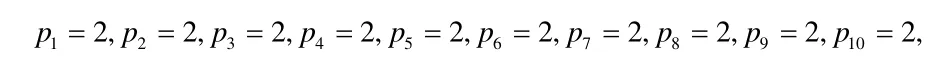
μ=0.25,η=0.75，它的反演數據結果見表1：

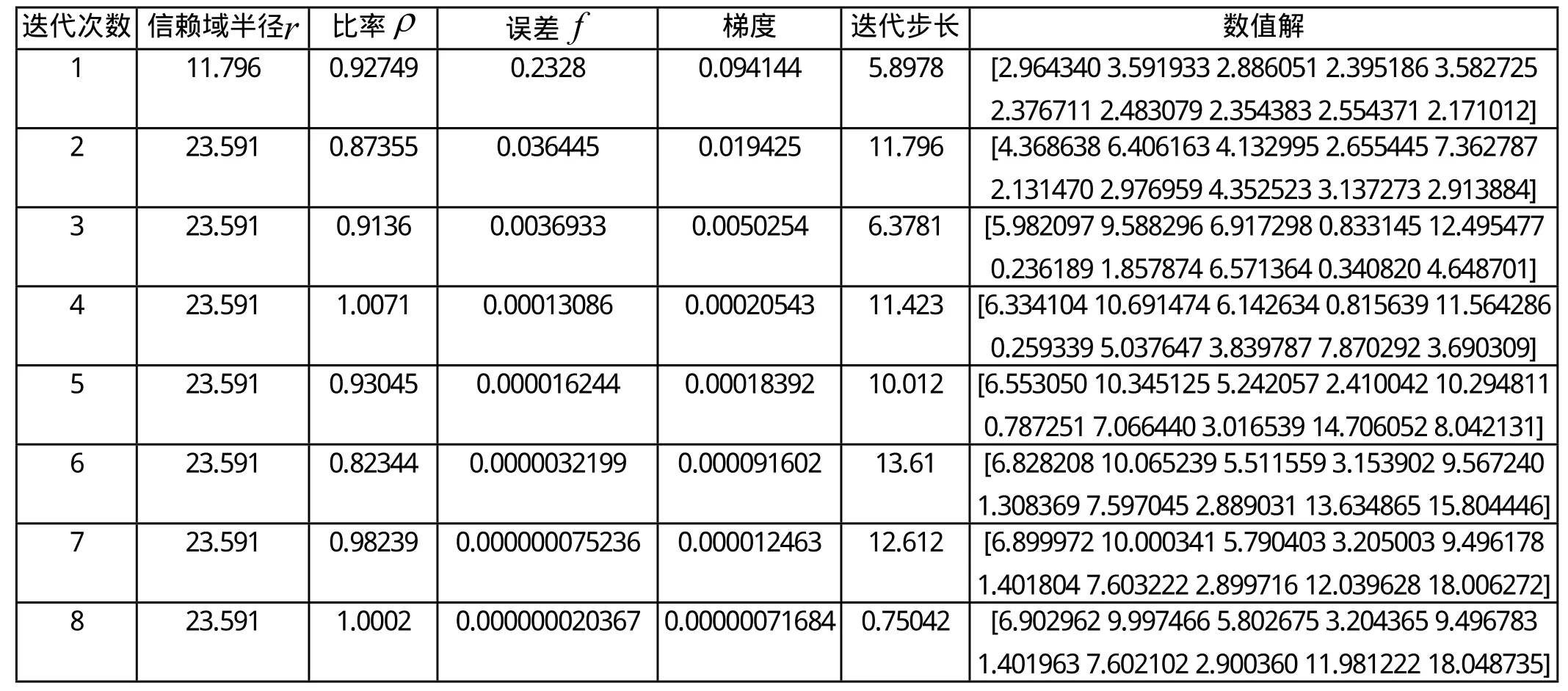
表1 參數反演數值模擬結果

從表1可以看出，經過8次迭代的反演值是與真值相比精度還要高。還可看到不同的初始猜測值得到了不同的反演結果，進一步知對參數的初始猜測值，信賴域算法并不敏感。

4 結語

本文對非線性動力系統中常微分方程的未知參數應用信賴域方法進行了反演，模擬數值的結果說明此算法的有效性。文中選擇了五個方程組和十個參數作為數值算例，證明了對多個方程組和多個參數信賴域算法也是可行的。

[1] 彭紹發.淺析易學在行政管理中的應用［J］.佳木斯大學社會科學學報，2011，29(1).

[2] 姜啟源，謝金星，葉俊.數學建模[M].北京：高等教育出版社.2003.

[3] 東北師大微分方程教研室.微分方程[M].北京：高等教育出版社.2005。

[4] 劉慧.宋廣華微分方程在數學建模中的應用探究［J］.科技信息（科學·教研）2008,6(13).