一種直線插補算法及其在機器人中的應用研究*

李進文，何素梅，吳海彬

(福州大學機械工程與自動化學院，福建福州350108)

0 引 言

工業機器人在搬運、碼垛、焊接、上下料等場合的應用越來越普遍，技術越來越成熟。很多經濟型工業機器人普遍選用通用的運動控制型PLC 作為機器人控制器。運動控制型PLC 有專門的高速脈沖輸出通道，可以通過對電機驅動器輸出脈沖實現單軸的運動控制。通常情況下，當機器人需要按照規劃的直線或曲線軌跡進行運動時，機器人控制器需要具備插補功能。在軌跡跟蹤精度要求不是很高的前提下，可以用直線插補替代圓弧插補實現曲線軌跡的運動，因此，直線插補是機器人實現插補運動最基本最重要的方法。有些運動控制型PLC 只提供單軸或多軸高速脈沖輸出功能，無插補指令;少數PLC 提供直線插補指令，但PLC 自帶的插補指令，其插補軸數一般為兩軸，并且這兩軸均為直線運動關節，即兩軸間插補的脈沖比例固定不變。而對于直線運動關節和轉動關節、或轉動關節與轉動關節之間的插補，這樣的插補指令并不能使用。

針對以上問題，有研究者開發了一套直線插補或者圓弧插補程序［1-4］，但所用方法并沒有充分利用PLC內置的脈沖輸出指令，插補脈沖頻率低、插補實時性差。通過采用專用的定位模塊也可以實現直線插補［5］，雖然提高了插補脈沖頻率，但大大增加了系統成本。有相關文獻提出利用PLC 本身內置的脈沖輸出指令［6-7］，開發高速直線插補程序，但是其只適用于插補軸為兩軸、插補的脈沖比例固定不變的場合。

針對以上問題，本研究提出了一種基于等時間間隔直線插補算法，該算法可以在任意結構形式的工業機器人上實現任意軸數的空間直線插補，適用于任意低成本的機器人控制器。

1 直線插補算法

基于等時間間隔的空間直線插補，就是在一個確定的時間間隔(也稱為插補周期)ΔT 內完成一次插補計算，為各坐標方向的運動提供一組數據。機器人控制器按照插補計算得到的數據，控制機器人各關節同時完成一次微小運動，從而使機器人執行器末端經過規劃的插補點［8-10］。

1．1 插補原理

機器人末端執行器在笛卡爾坐標系中的描述，包括位置描述與姿態描述，因此其插補算法中也包括位置插補與姿態插補。姿態插補一般采取線性方式，即把末端執行器在曲線上的終點和起點的方位差均勻地分配到插補的每一步，算法簡單，本研究不作討論。位置插補，就是求出在一個插補周期內，機器人末端執行器從當前位置(Xi，Yi，Zi)沿插補直線方向截取線段長ΔL(ΔL 取決于插補速度V、加減速時間Ta)后，所到達的下一個插補點位置(Xi+1，Yi+1，Zi+1)。

1．2 插補遞推公式

已知空間插補直線的起點坐標P1(x1，y1，z1)和終點坐標P2(x2，y2，z2)，其中P1，P2為相對于基座坐標系的坐標點，可以通過示教得到。設V 為沿插補直線方向的運動速度，ΔT 為插補周期，Ta為插補運動的加減速時間。

基于此可以求出直線軌跡長度:

(1)插補直線的長度L:

(2)插補總步數N:不考慮加減速的情況，可得理論插補步數N0:

實際上，考慮到機械臂的慣性以及高速脈沖輸出通道對初始脈沖頻率的限制，應該在插補直線的首尾分別設置加、減速段，因此實際的插補總步數應大于理論插補步數。由插補運動的加減速時間Ta可求得笛卡爾坐標系下的加減速度a:

加減速段的插補步數Na:

從而，得到實際插補總步數N:

(3)確定插補點與插補起點的距離Si:根據加減速特性的相關參數可計算出任意插補點Ni(i=1～N)與插補起點P1的距離Si:

(4)確定插補點Ni的坐標:插補起點P1(x1，y1，z1)與Si在笛卡爾坐標系三坐標軸方向上的分量疊加，即可得到各插補點在笛卡爾坐標系下的坐標(Xi，Yi，Zi):

式中:ΔX=x2－x1;ΔY=y2－y1;ΔZ=z2－z1。

由插補遞推過程知，插補點總在插補直線上，算法沒有累積誤差。求得各插補點的坐標后，再通過機器人運動學逆解，即可求得各插補點對應的關節變量。

對于不同的控制器，特別是PLC，由于存儲空間有限，其所能存儲的插補點數據是有限的。上述算法中插補周期ΔT 可以根據控制器的存儲空間以及插補直線的數量進行選擇，從而可以降低對控制器的性能要求。

2 插補算法的應用

以實驗室自行研發的四關節沖床上下料機器人為研究平臺，探討并驗證上述算法。該機器人結構示意圖和實物圖如圖1 所示。

圖1 四關節沖床上下料機器人

利用D-H 法建立機器人坐標系，可得到機器人末端執行器的正運動學方程為:

逆運動學方程為:

由于關節4 的運動只對機器人末端執行器的姿態產生影響，這里不予討論。

2．1 插補算法在PLC 上的實現

機器人控制器選用松下FP-X C60T 運動控制型PLC，其內置兩個頻率范圍1．5 Hz～100 kHz 和兩個頻率范圍1．5 Hz～20 kHz 的脈沖輸出通道，具有強大的浮點和三角函數運算功能，非常適合算法編程［11］。PLC 上的直線插補程序流程圖如圖2 所示。以下通過流程圖2 重點說明插補算法在PLC 上的實現。

插補程序采用絕對值式脈沖輸出。插補運動開始前先建立數據表，數據表結構如圖3 所示。數據表由連續的雙字組成，分別是控制代碼、頻率、目標脈沖值及脈沖輸出停止標志組成。其中控制代碼以位為單位使用，包括占空比、頻率范圍選擇、脈沖輸出模式、脈沖輸出方式等。

圖2 PLC 上的直線插補程序流程圖

圖3 PLC 的數據表結構

本研究在建立數據表前，先求出只需計算1 次的初始數據，為計算插補點做準備。之后，根據插補步數選擇加速段—勻速段—減速段距離，獲得插補點坐標。通過機器人運動學逆解，即可求得各插補點對應的關節變量，進而求得插補點及每一步對應的各關節目標脈沖和脈沖頻率。控制數據表每一組頻率及目標脈沖值對應一個插補點。插補計算結束時，建立運動控制數據表，并同時啟動各通道脈沖輸出，直到所插補直線脈沖輸出完成，結束插補程序。

上述插補程序約800 步，PLC 平均掃描時間為25 ms。

2．2 誤差的定性分析

2．2．1 插補程序造成的誤差

由于機器人結構的關系，求得各插補點坐標進而求取各插補點及每一步對應的各關節目標脈沖和脈沖頻率時，可能得到某兩點之間的目標脈沖值相等的情況(即［S+2(N+1)］=［S+2(N +3)］)。此時，若不對目標脈沖值進行修正，會造成實際輸出脈沖數量與指定脈沖數值不同。本研究所采取的修正方法為:當出現上一插補點的目標脈沖值與當前插補點的目標脈沖值相等時，將當前插補點的目標脈沖值加1，使其與上一插補點的目標脈沖值不一致。設當前插補點目標脈沖值修正后對應的坐標為N'i(X'i，Y'i，Z'i)，修正后各關節變量與修正前各關節變量差值Δθ1、Δd2、Δd3(即Δθ1=δ1，Δd2=δ2，Δd3=δ3)。此時，插補點定位誤差δi:

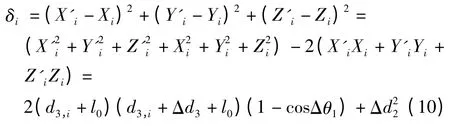
筆者所研究的機器人，各關節脈沖當量分別為δ1=0．002 5 rad、δ2=0．025 mm、δ3=0．013 mm，將上述數據帶代入式(10)，得到修正后插補點定位誤差δi≈6．25 ×10－4mm，可以滿足實際使用。

2．2．2 最低脈沖頻率造成的誤差

由于PLC 硬件上最低脈沖頻率的限制，求得的兩插補點間對應的各關節脈沖頻率可能低于允許最低脈沖頻率，此時PLC 會以最低脈沖頻率進行脈沖輸出，這樣，在某個插補點的運動上一個關節先于另一個關節完成脈沖輸出，造成插補誤差。最低脈沖頻率造成的誤差如圖4 所示。粗實線是理想的插補直線，虛線是為滿足最低脈沖頻率限制要求得到的實際插補直線。

圖4 最低脈沖頻率造成的誤差

3 實驗及結果分析

為驗證插補算法在自行研發的四關節沖床上下料機器人的應用效果，本研究設計實驗如下:機器人以起點P1(－926． 57，535． 03，50)，終點P2(－1 144．43，659．60，186．60)做直線插補，其中:V =240 mm/s，ΔT =50 ms、Ta=200 ms，實際插補軌跡如圖5 所示。由于機器人在運動過程中、特別是在加減速階段存在一定的抖動情況，以及傳動系統少許的間隙，致使機器人在實際運動過程中末端操作器的軌跡偏差還會更大一些。

圖5 插補直線的實際軌跡

插補過程中，每10 ms 采樣一次PLC 各脈沖通道輸出的絕對脈沖值，結合機器人結構，得到插補直線采樣點的空間坐標如圖6 所示。從圖6 可以看出，空間上插補直線可以比較好的跟蹤理論直線軌跡。

圖6 插補直線與理論直線的空間重合度

為進一步定量分析插補直線對理論直線的跟蹤精度，以插補直線為橫坐標，插補直線與理論直線對應采樣點的距離為縱坐標，作圖得到插補直線對理論直線的跟蹤精度如圖7 所示。跟蹤誤差小于0．3 mm，滿足機器人直線插補的精度要求。雖然插補直線不能與理論直線完全重合，但其基本與理論直線平行，如圖6 中插補直線與理論直線的局部放大圖所示。如果需要提高直線插補跟蹤精度，則需要減小插補周期，增加插補點數，但這反而會提高對控制器的性能要求。

圖7 插補直線對理論直線的跟蹤精度

4 結束語

本研究針對工業機器人在笛卡爾坐標系中的空間直線軌跡規劃問題，提出了一種基于等時間間隔的直線插補算法。該算法可以在任意結構形式的工業機器人上實現任意軸數的空間直線插補，對于有直線插補要求、但跟蹤精度要求不高的應用場合，可以通過適當增加插補周期、減少插補點數的方法降低控制器的硬件配置，從而降低機器人系統成本。所述算法已成功應用在自行研發的四關節沖床上下料機器人上，實際應用表明了該直線插補算法的有效性，具有一定的應用價值。

今后將通過其他機器人平臺來進一步驗證提出的直線粗插補算法的有效性。同時，考慮到圓弧插補算法在機器人曲線軌跡規劃中應用的普遍性，今后將進一步探討圓弧插補算法及其在低配置控制器上的實現。

［1］張鐵異，黃柄瓊，盧福寧，等．基于松下電工FPl 型PLC 的直線插補程序設計［J］．裝備制造技術，2007(10):68-70．

［2］黃菊生，龔慶壽，夏 平，等． 數控平臺PLC 控制系統的開發［J］．機床與液壓，2005(4):56-58．

［3］孫建仁．步進電機的PIE 控制系統設計［J］．機械研究與應用，2001(4):23-26．

［4］趙燕偉，朱雙勝，盧 東，等．基于直線插補的字體邊緣識別技術［J］．機電工程，2009，26(5):52-54．

［5］譚懷亮，劉 曉，賀再紅．基于三菱PLC 的刨床數控系統［J］．機械與電子，1999(6):51-53．

［6］任善巖． PLC 直線插補方法的研究［J］． 機床與液壓，2009，37(9):56-58．．

［7］葉伯生．計算機數控系統原理、編程與操作［M］．武漢:華中理工大學出版社，1999．

［8］金建新．機床CNC 系統中任意空間曲線的可控步長插補方法［J］．機械工程學報，2002(4):95-97．

［9］ADACHI H． Line interpolation apparatus and line interpolation method:U．S． Patent 6，636，267［P］．2003-10-21．

［10］席港港，趙慶志，王 軍，等．傳統逐點比較法直線插補方法的改進［J］．山東理工大學學報:自然科學版，2012，26(1):67-69．

［11］Matsushita Electric Works，Ltd．． FP Series Programming Manual［Z］．Matsushita Electric Works，Ltd．，2012．