非連續路段下移動機器人的軌跡跟蹤

孟 靜 ，高曉丁 ，陳 罡

(1．西安工程大學機電工程學院，陜西西安710000;2．浙江紡織服裝學院機電學院，浙江寧波315200)

0 引 言

基于視覺的移動機器人軌跡跟蹤已成為研究熱點，目前對移動機器人的軌跡跟蹤多是連續路段。如在自動化生產車間里，機器人沿著固定軌跡完成搬運貨物等重復性的工作;在醫院里機器人充當傳送病歷及常用資料的傳遞員等［1］。文獻［2］基于Backstepping 思想設計了一種滑模變結構軌跡跟蹤控制系統，很好實現了移動機器人的軌跡跟蹤。文獻［3］采用Lyapunov 函數直接法提出了一種軌跡跟蹤控制算法，分析了系統的漸進穩定性。對于移動機器人在非連續中的運動情況，目前尚未有系統的研究，本研究就輪式移動機器人在非連續路段中如何實現精確的軌跡控制等問題進行討論。

對于路面狀況的分析，目前多是針對于道路裂縫等問題進行研究，本研究在裂縫的識別與算法的基礎上，對非連續路段問題進行深入分析與研究，通過合理的算法實現對移動機器人在非連續路段中的穩定控制。

1 運動學模型及目標信息的獲取

1．1 運動學模型

筆者研究的輪式移動機器人采用兩個驅動輪、一個萬向輪的結構。左、右兩個驅動輪安裝在同一軸線上，分別安裝兩個電機驅動機器人運動，當兩個電機的轉動速度不同時，左、右兩輪將會產生差動，則可實現移動機器人的轉彎動作［4］。由于萬向輪僅起支撐作用，故忽略其在運動學模型中的作用，建立的移動機器人的運動模型如圖1 所示。

圖1 運動學模型

機器人的位姿可由它中心所在點的坐標及方向角表示，令:

Pc=(xc，yc，θc)T，q=(v，w)T

式中:(xc，yc)T—移動機器人的位置;θc—移動機器人前進方向與x 軸的夾角;v，w—移動機器人的線速度和角速度。

它們在運動學模型中是控制輸入，移動機器人的運動學方程為:

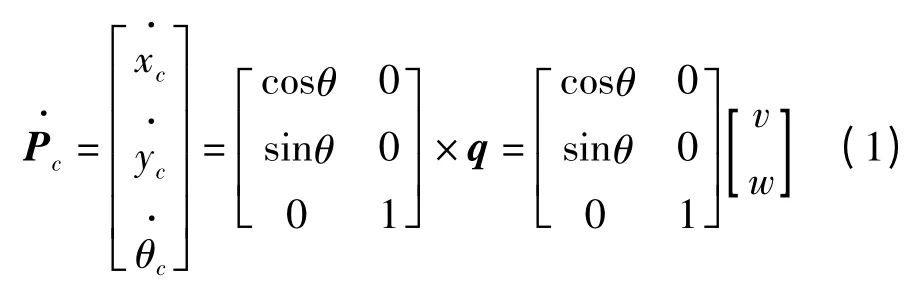
本研究中的軌跡跟蹤是讓機器人沿著給定路徑行走，當機器人從當前位姿Pc=(xc，yc，θc)T移動到目標位姿Pr=(xr，yr，θr)T時，產生了一個新的坐標系xe－ye，令移動機器人的位姿誤差為Pe=(xe，ye，θe)T，其中，θe=θr－θc。設新坐標系xe－ye與原坐標系x－y之間的夾角即為θc，可以得到機器人位姿誤差方程:

位姿誤差微分方程為:

由以上分析可知，移動機器人運動學模型的軌跡跟蹤可以定義為尋找有界輸入v 和w，使對任意初始誤差，位姿誤差微分方程在該控制輸入作用下有界且=0。

1．2 攝像機的標定

攝像機的標定方法一般是在攝像機前放置一個立體標靶，用上面位置已知的點作為特征點，采集標靶圖像后，利用這些點的圖像坐標和三維空間坐標建立方程，解方程即可獲得攝像機的內、外參數［5］。本研究采用Faugeras 的線性模型攝像機標定法對攝像機進行標定。設點的世界坐標系已知，攝像機的內參數模型為:

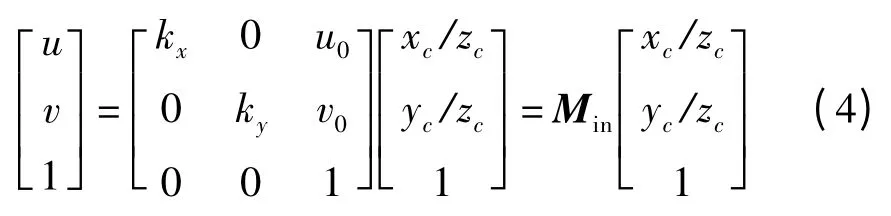
式中:Min—攝像機的內參數矩陣;(xc，yc，zc)—景物點在攝像機坐標系下的坐標;(u，v)—景物點的圖像坐標。

攝像機的外參數模型為:

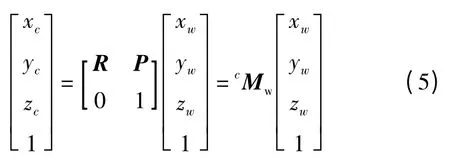
式中:(xw，yw，zw)—景物點在世界坐標系下的坐標且已知;cMw—外參數矩陣。

由式(4，5)可得:

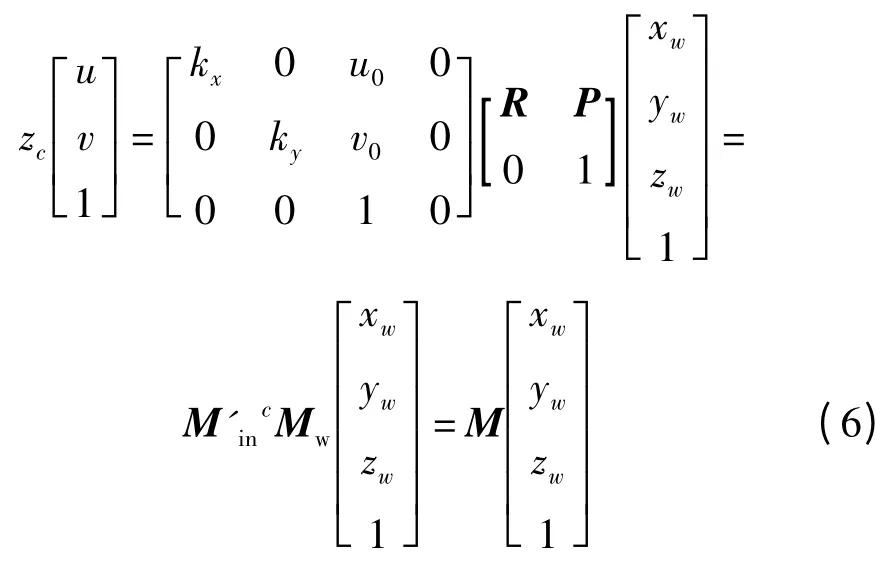
將式(6)展開并消掉zc后，得下式:

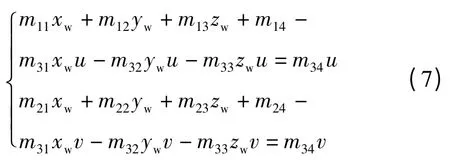
由于空間的每個點都符合式(7)兩個方程，于是可得式(8)所示矩陣:

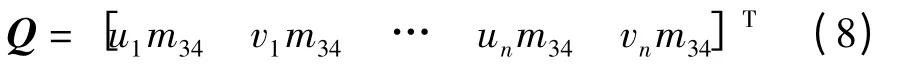
將外參數矩陣cMw和M 矩陣寫成式(9)形式，可得式(10)所示矩陣:

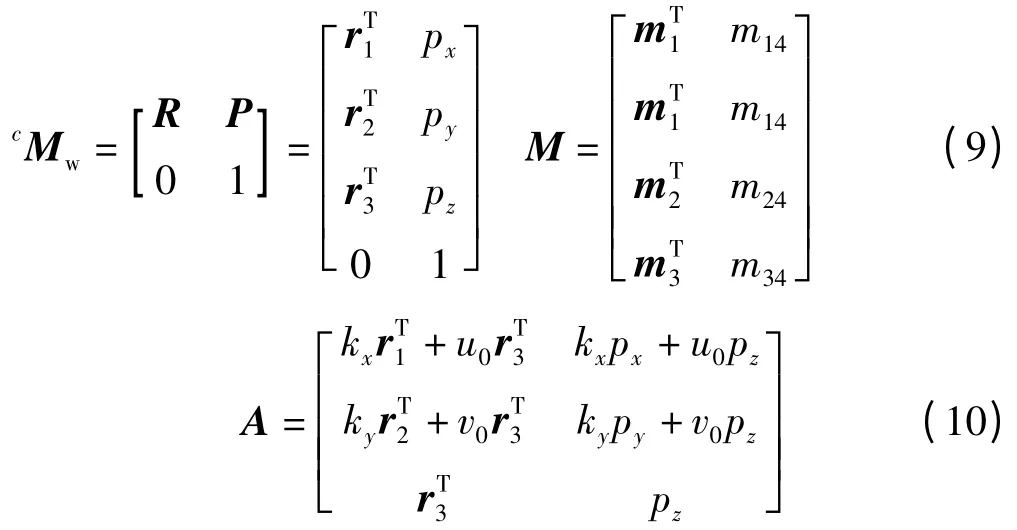
cMw中的R 是單位正交矩陣。利用單位正交矩陣的性質，可以從M 矩陣中分解出攝像機的內外參數，如下式:

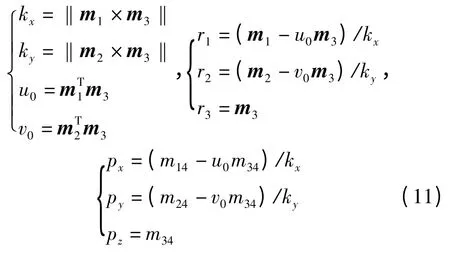
求出以上參數即可完成對攝像機的標定。

1．3 軌跡信息的獲取

本研究采用雙目立體視覺系統確定空間目標點相對于攝像機的三維空間位姿。設兩臺攝像機C1和C2的內參數采用四參數模型，相對外參數用c1Mc2表示。空間點P 在攝像機C1中的圖像坐標為(u1，v1)T，則像點坐標P1c1表示為:

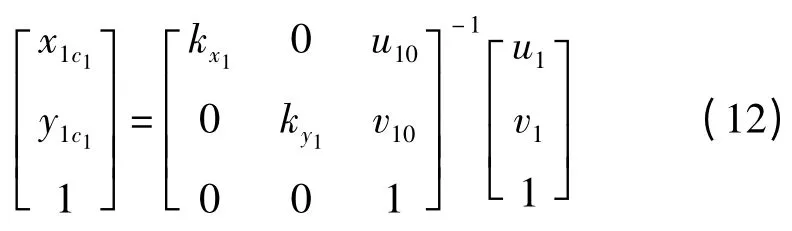
空間點P 在攝像機C1光軸中心點與點P1c1構成的直線上，即符合方程:

將點P1c2在C2中的坐標轉換為在C1中的坐標，如下式:

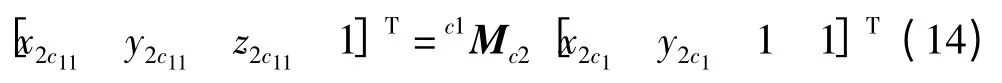
同理可求得點P 在C2中的像點坐標以及方程

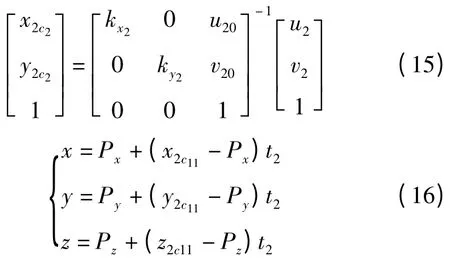
式(16)中Px、Py和Pz構成c1Mc2的位置偏移量。直線方程(13，16)的交點即為空間點P。至此可以求出空間點的坐標，同理可以通過判定其他點的位置獲取目標軌跡［6-7］。

2 道路模型

2．1 連續路段

當為連續路段時，本研究選取直線模型y =kx +b作為軌跡模型，然后利用路徑線上的n 個像素點(假設像素點坐標為(ai，ci)其中n ＞1，1≤i≤n)和最小二乘法對路徑線模型的參數k 和b 進行擬合計算［8］:

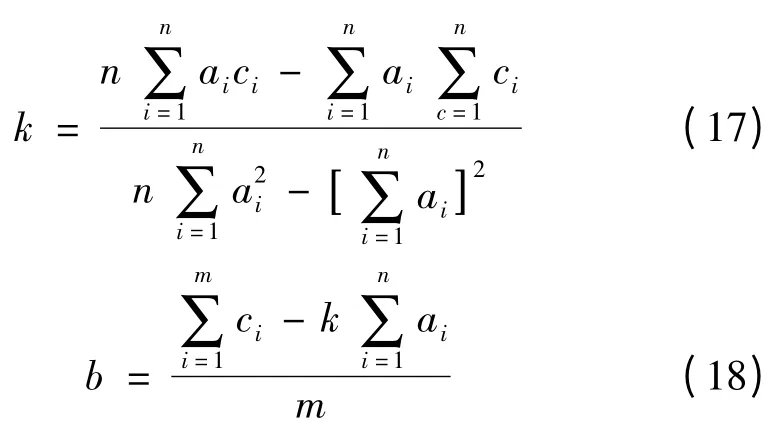
最后，根據計算出的直線模型即可確定移動機器人的期望跟蹤軌跡。

2．2 非連續路段

當移動機器人在軌跡跟蹤過程中出現如圖2 所示的非連續路段時，需先將攝像頭采集到的圖像進行圖像預處理，突出圖像中的非連續路段，再運用二值化的方法進行圖像區域分割，提取出圖像中非連續路段信息［9-10］。

二值化方法的關鍵在于閾值的選取與設定，本研究主要采用大津法進行閾值的確定，該方法的原理如下:

設圖2 中圖像的灰度值集合為P={0，1，2，3，…，255}，灰度值為j 的像素個數為mj，則整幅圖的像素總數為:

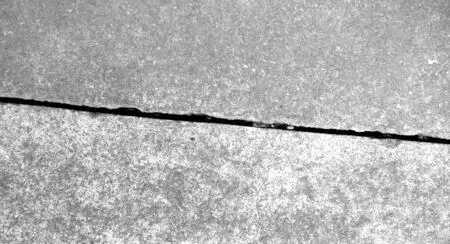
圖2 非連續路段

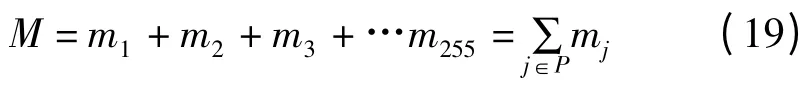
則對應灰度值為j 的像素概率分布為:

式中:j∈P，Qj≥0，Qj=1。

則整幅圖像的灰度平均值μ，方差σ2可表示為:

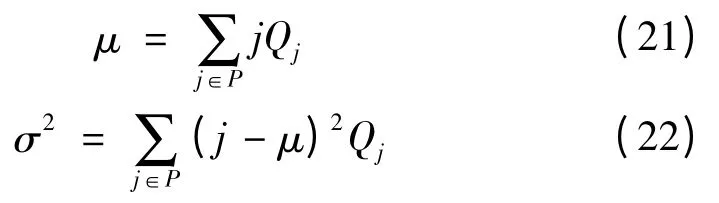
假若整幅圖像以灰度值作為閾值，那么將圖像分割成為P1={0，1，…T}，P2={T +1，T +2，…255}兩個類Z1，Z2，此時，類Z1和類Z2發生的概率P1，P2，可以表述為:

并且有P1+P2=1。

從而這兩類的均值分別為:

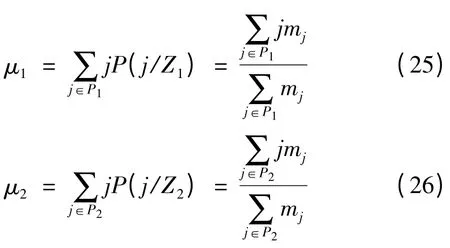
這兩類的方差分別為:

這樣就可以得到圖像的類間方差為:

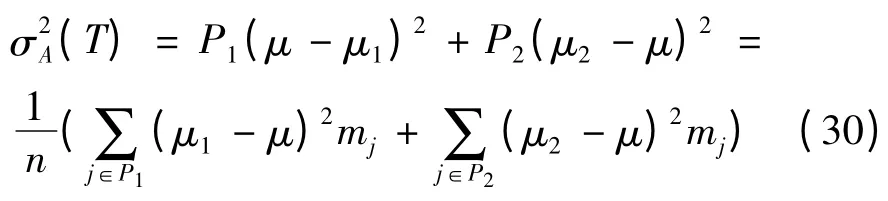
圖3 非連續路段的二值化圖像

在檢測到非連續路段后，還需計算非連續路段的寬度，看其是否超出機器人行走的安全范圍，計算方法為［11］:

(1)求出二值非連續路段圖像水平投影Y。

(2)設在坐標點j 處的投影值為pro［j］，pro［j］大于0。

(3)遍歷二值非連續路段細化圖像，選取j(j，y)點及其相鄰點i(i，x)，計算此處裂縫的傾角α。

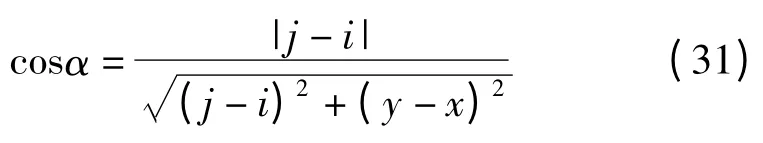
(4)計算裂縫寬度值W［j］。

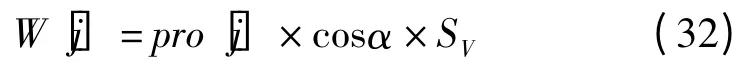
(5)對各個投影點為橫坐標的非連續路段點處的寬度都進行上述計算，最大值即為非連續路段點的最大寬度。

當所計算出的非連續路段點的寬度在機器人行走的安全范圍內時，機器人按照所給的軌跡繼續追蹤，當超出機器人行走的安全范圍時，機器人將停止或后退。

3 軌跡跟蹤

3．1 軌跡跟蹤控制原理

在機器人的運動過程中，可通過機器人的幾何中心坐標，生成實際運動軌跡曲線，并比較實際運動軌跡與理論運動軌跡的差值。當二者誤差小于θα時，不需要對機器人的運動進行糾正;當二者的誤差超出θα時，則可根據設定的算法程序，控制機器人左、右電機以不同的速度轉動，完成對機器人運動位姿的糾正與誤差補償，從而實現對機器人運動的閉環控制與自動跟蹤。經過反復控制器調節，最終使得系統位姿誤差Pe趨于零。移動機器人的軌跡跟蹤框圖如圖4 所示。

3．2 控制器的設計

為了使移動機器人的跟蹤誤差快速收斂于零，獲得良好的軌跡跟蹤效果，本研究設計了基于Lyapunov函數的控制器［12-14］，其控制律如下:

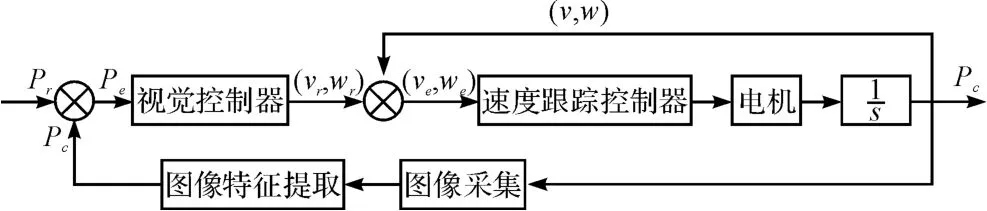
圖4 軌跡跟蹤控制框圖

令控制參數a1，a2，aθ有界，且都大于零。

構造Lyapunov 函數為:

結合式(2，3)對式(34)求導得:

將式(33)代入式(35)得:

根據Lyapunov 穩定性判據可知，當a1，a2，aθ有界且都大于零時，用式(33)表示的控制率能使輪式移動機器人位姿誤差趨近于零。

4 仿真試驗

為了驗證控制算法的有效性，本研究用Matlab 進行算法編程，對機器人直線軌跡跟蹤的連續路段和非連續路段進行仿真［15-16］。算法程序流程圖如圖5 所示。參考軌跡的初始位置為xr(0)=0，yr(0)=0，θr(0)=π/4 控制輸入為v=0．2 m/s，w=0，角度誤差θα=7°，移動機器人的初始位置為xc(0)=1．5，yc(0)=1．5，θc(0)=2π/3;控制參數a1=a2=10，aθ=50，裂縫寬度的安全值為W［j］=5 mm，SV=2;直線軌跡跟蹤效果圖如圖6 所示;當為連續路段時，仿真結果如圖7 所示。當t=3．2 s 出現非連續路段時，非連續路段寬度安全范圍如圖8 所示，非安全范圍如圖9 所示。

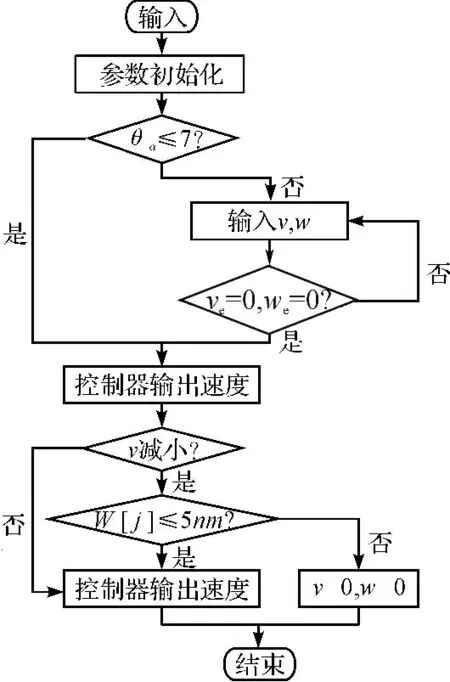
圖5 算法程序流程圖

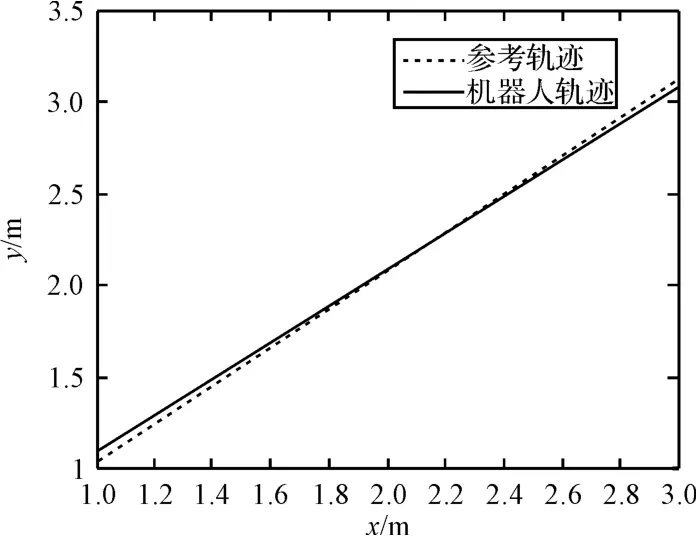
圖6 直線軌跡跟蹤效果圖

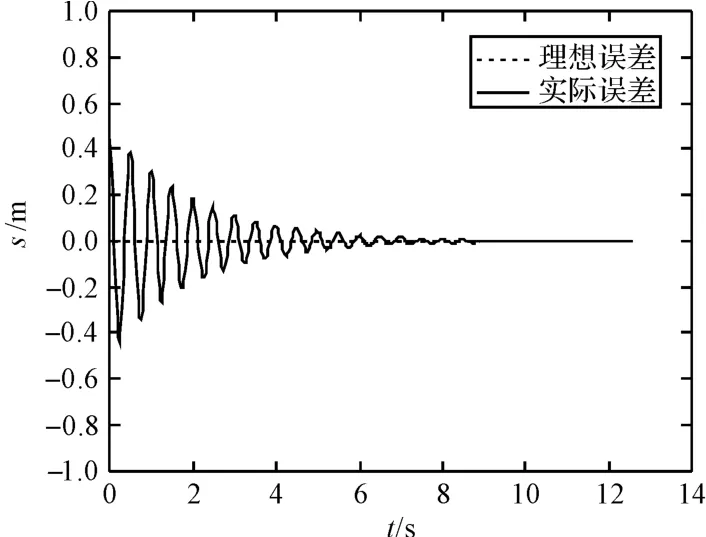
圖7 連續路段軌跡跟蹤效果圖

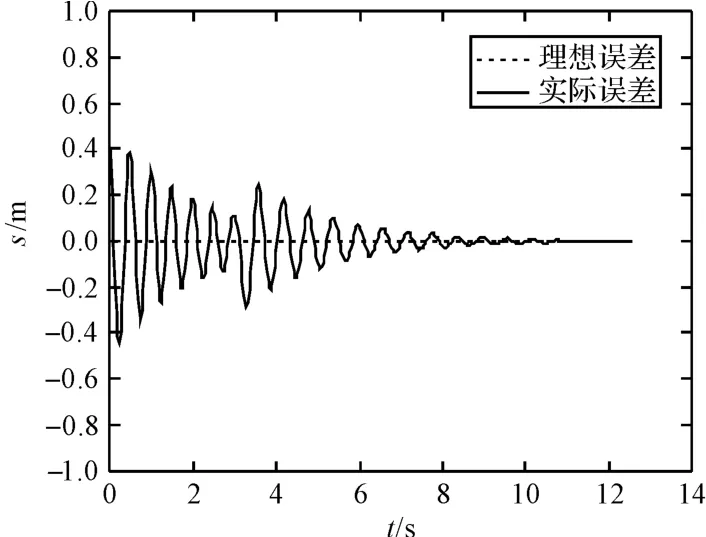
圖8 非連續可走路段軌跡跟蹤效果圖

移動機器人的跟蹤結果與偏差變化如圖6 所示。機器人在連續路段中的軌跡跟蹤情況如圖7 所示;圖8 中，機器人在t=3．1 s 時遇到非連續路段，其寬度小于5 mm，故機器人可以行走，但在此刻位移誤差出現了波動，在t=10 s 時實現了穩定跟蹤，收斂到理想軌跡;圖9 中在t=3．2 s 時遇到非連續路段，其寬度大于5 mm，機器人不可以行走，故最終停留原地;圖10 中在t=2．5 s 時位姿誤差收斂到零，從而驗證了所設計的控制率能夠實現移動機器人對給定軌跡的跟蹤。

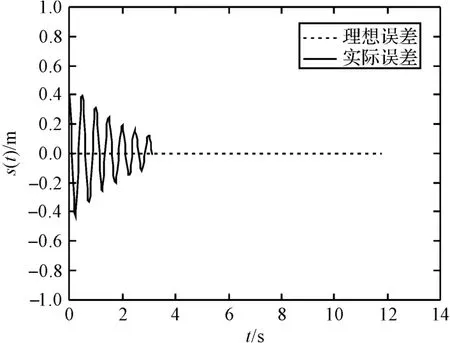
圖9 非連續不可走路段軌跡跟蹤效果圖

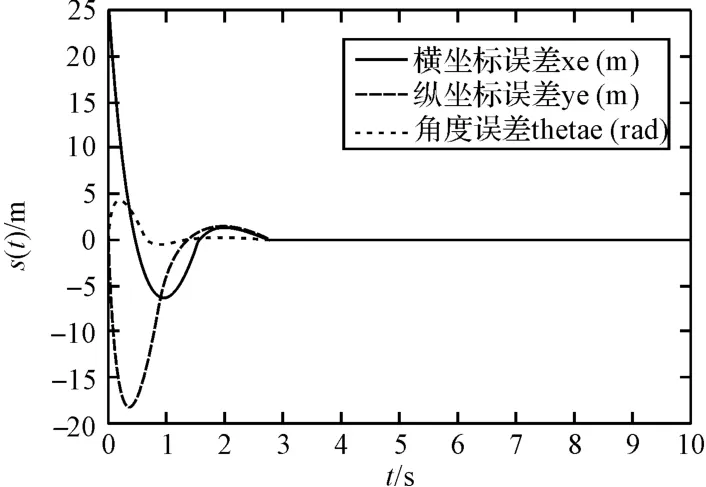
圖10 位姿誤差變化曲線

5 結束語

本研究討論了移動機器人在非連續路段下的軌跡跟蹤問題，利用二值化方法對非連續路段圖像進行處理，通過大津法對閾值進行確定來提取圖像的非連續路段信息，并設計了基于Lyapunov 函數的控制器實現了機器人對給定軌跡的跟蹤，最后用Matlab 進行仿真，仿真結果證明了該控制率及算法的可行性。通過對非連續路段的處理，使機器人能夠更好地實現對道路軌跡的跟蹤，防止機器人在運行過程中因路面的破損而損壞機器人。

與其他算法進行比較，大津法能夠選取出理想的閾值，但在很多情況下不是最佳的分割，在后續內容中，本研究將著重于最佳閾值的分割進行研究。

［1］日本機器人學會．機器人技術手冊(新版)［M］．宗光華，稱君實譯．北京:科學出版社．2008．

［2］GREYY W，PONDAR． The URANUS mobile robot［R］．The Robotics Institute Technical Report． Carnegie-Mellon University，1986:127-129．

［3］胡浚濤，李亞榮，李 林．輪式移動機器人軌跡跟蹤控制研究［J］．儀表技術，2013(4):27-28．

［4］上官望義．輪式移動機器人移動性能研究及樣機設計開發［D］．西安:西安理工大學機儀學院，2009．

［5］王寶磊，王朝立，李 菲，等．基于雙目視覺伺服反饋的非完整移動機器人軌跡跟蹤［J］． 測控自動化，2012，28(10):125．

［6］張顯偉，吳忠偉，張鳳海，等．移動機器人模糊滑模軌跡跟蹤控制［J］．長春工業大學，2013，34(4):374-375．

［7］曹 洋，項龍江，徐心和．基于全局視覺的輪式移動機器人軌跡跟蹤控制［J］．機器人，2004，26(1):79-82．

［8］李晉蕙． 用圖像處理的方法檢測公路路面裂縫類病害［J］．長安大學學報:自然科學版，2004，24(3):25-29．

［9］肖旺新，張 雪，黃 衛，等．路面破損自動識別的一種新算法［J］．公路交通科技，2005，22(11):75-78．

［10］孫波成，邱延峻． 基于圖像處理的路面裂縫識別研究［J］．重慶交通大學學報:自然科學版，2008，27(1):62-64．

［11］肖 靖．道路裂縫識別算法研究［D］．北京:北京郵電大學理學院，2009．

［12］劉 磊，向 平，王永驥，等．非完整約束下的輪式移動機器人軌跡跟蹤［J］．清華大學學報:自然科學版，2007，47(S2):1885-1889．

［13］岳龍旺，朱敬花．基于輪式移動平臺的新型濕式清潔機器人系統［J］．輕工機械，2013，31(6):66-68．

［14］羅 劍，雷 勇．智能移動機器人中視覺跟蹤算法研究［J］．儀器儀表學報，2009，30(6):336-340．

［15］晏祖根，李 明，徐克非，等．高速機器人分揀系統機器視覺技術的研究［J］．包裝與食品機械，2014(1):28-31．

［16］劉金琨．機器人控制系統的設計與Matlab 仿真［M］．北京:清華大學出版社，2008．