一類食餌染病且垂直傳染的生態流行病擴散模型的整體性態

陳安寧

(隴東學院 數學與統計學院, 甘肅 慶陽 745000 )

一類食餌染病且垂直傳染的生態流行病擴散模型的整體性態

陳安寧

(隴東學院 數學與統計學院, 甘肅 慶陽 745000 )

研究一類具有空間擴散和食餌染病且垂直傳染的生態—流行病模型的整體性態.首先討論解的存在唯一性和一致有界性; 其次由線性化方法得到了該模型非負平衡點的局部漸近穩定的充分條件, 并構造恰當的 Lyapunov泛函證明非負平衡點的全局漸近穩定性, 得到了捕食者滅絕、疾病消失和疾病成為地方病的充分條件.

垂直傳染; 空間擴散; 生態流行病模型; 穩定性

0 引 言

1927年Kermack等開創性的構造了著名的SIR倉室模型后 , 流行病模型的研究越來越受到重視[1-6]. 文獻[1]研究了疾病僅在食餌中傳播的捕食者—食餌模型. 文獻[3] 研究了疾病在食餌和捕食者之間傳播的捕食者—食餌模型. 此外還有許多傳染病模型[5-6], 但某些傳染病能夠垂直傳染, 文[4]首先建立并討論了如下捕食者—食餌系統中食餌染病且垂直感染的傳染模型給出了非負平衡點的存在條件, 并得到了非負平衡點局部和全局穩定的充分條件. 然而, 很少有關于帶流行病種群擴散模型解的定性性質的已知結果. 本文將主要討論在Neumann邊界條件下具有空間擴散和食餌染病且能夠垂直傳染的捕食者—食餌模型解的一致有界性,平衡點的局部漸近穩定性和全局漸近穩定性, 其中Ω?是邊界?Ω光滑的有界區域,η是?Ω上的單位外法向量,?η=?/?η;u1,u2分別表示食餌中易感者和感染者種群密度,u3表示捕食者的密度;K,a,b,d,β,δ,ri(i=1,2),di(i=1,2,3) 都是正常數;di是種群ui(i=1,2,3)的擴散系數.ri為食餌中易感者和感染者的內稟增長率, 由于要考慮因病死亡,所以r1>r2;K為環境最大容納量;β為傳染率;a,b為捕食系數,b≥a表示捕食者更易捕到染病的食餌;δ為消化系數;d表示捕食者的死亡率.

(1)

(2)

本文內容安排如下: 第2節討論解的一致有界性. 第3, 4節分別討論平衡點的局部漸近穩定性和全局漸近穩定性.

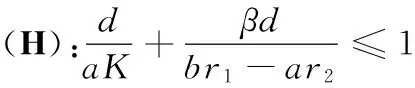
1 一致有界性

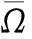
其中

M2是依賴于|Ω|(2)的系數及初值u0,v0的正常數.

(2)中的3個方程在Ω上積分并求和, 得

‖ui(x,t)‖L∞(Ω)≤M2,i=2,3,

M2是依賴于Ω,(2)的系數及初值ui0(i=1,2,3)的正常數.故T=+∞.

2 平衡點的局部穩定性

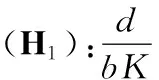
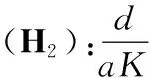
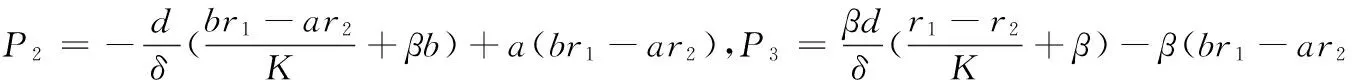
(2)對應的常微分方程組在E0(0,0,0),E1(K,0,0) 處不穩定. 而(2)對應的常微分方程組的解是(2)的特解, 從而E0(0,0,0)和E1(K,0,0) 也是(2)的不穩定的平衡點. 下面討論平衡點E2,E3,E4,E5的穩定性.

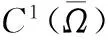
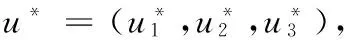
(2)在u*處的線性化方程為ut=Lu.對任i≥1,Xi是算子L的不變子空間,λ是算子L在Xi上的特征值當且僅當λ是-μiD+Fu(u*)的特征值.-μiD+Fu(u*)的特征方程為

λ3+A1iλ2+A2iλ+A3i=0,

其中

A1i=μi(d1+d2+d3)+B1,

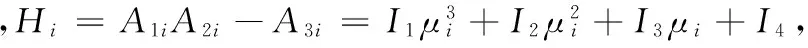
I1=(d1d2+d1d3+d2d3)(d1+d2+d3)-d1d2d3,

I2=-{(a11+a22)[d1d2+d3(d1+d2+d3)]+(a11+a33)[d1d3+d2(d1+d2+d3)]+(a22+a33)[d2d3+d1(d1+d2+d3)]},

I3=B2(d1+d2+d3)-B1[d1(a22+a33)+d2(a11+a33)+d3(a11-a22)]- [d1(a22a33-a23a32)+d2(a11a33-a13a31)+d3(a11a22-a12a21)]=d1[B2+(a11+a22+a33)(a22+a33)-a22a33+a23a32]+d2[B2+(a11+a22+a33)(a11+a33)-a11a33+a13a31]+d3[B2+(a11+a22+a33)(a11+a22)-a11a22+a12a21],

那么I1,I2,I3,I4均大于0, 故Hi>0.又A1i>0,A3i>0.根據Routh-Hurwitz判別法得, 對任i≥1,λi1,λi2,λi3均有負實部.

下證存在正常數δ, 對任意i≥1有

Re{λi1},Re{λi2},Re{λi3}≤-δ.

(3)

令λ=μiξ，則

當i→∞時，μi→∞有

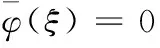
那么，當i≥i0時

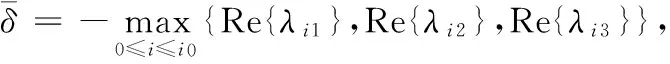
注1 文[4]給出了常微分方程組(2)與定理2和定理3類似的結果，且穩定的條件一致.

3 平衡點的全局穩定性

本節應用Lyapunov泛函方法討論問題 (2)的平衡點E2,E3,E4和E5的全局漸近穩定性.

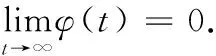
設u是(2)唯一的正解，由定理1和文[10]定理A2知，對任t0>0有

(4)

其中α∈(0,1)，C是不依賴于t的正常數.

證明 構造如下Lyapunov函數

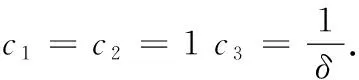
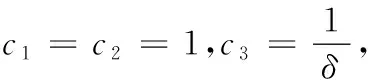
如果條件(H3)成立，則上述二次型正定，從而存在正常數δ1>0，使得

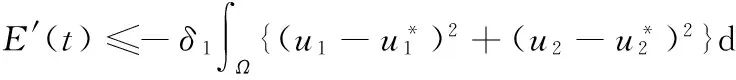
(5)

仍由(4)知ψ′(t)在[t0,∞)有界，t0>0.應用引理1得，當t→∞時ψ(t)→0,即

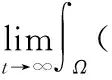
由Pioncaré不等式得

(6)

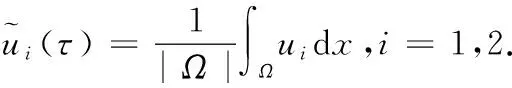
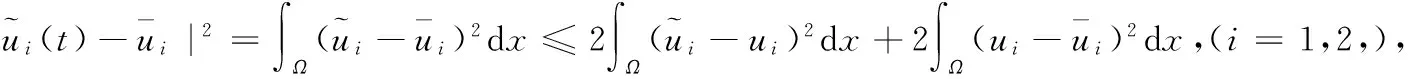
由(5)，(6)得

(7)

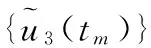
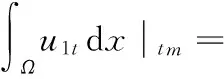
另一方面

(8)

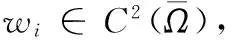
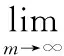
根據(5)-(8)有

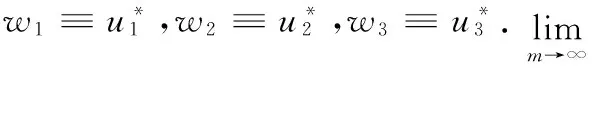
類似于定理2的討論, 可得如下定理：

證明(i)構造如下Lyapunov函數

其中ci為待定正常數.

(ii)定義如下Lyapunov函數

其中ci為待定正常數.

其它的證明與定理4類似, 在此不再贅述.

證明 定義Lyapunov函數如下

其中ρ=λ=δ. 由強極值原理知, 在初值滿足條件u10,u20,u30≥(?)0時,問題(2)的解在任正時刻為正函數.從而E(t)關于(1)的正解u(t)滿足

如果取ρ=λ=δ,第4,第5項為0; 經簡單計算知,條件(H4)保證d-ρbK>0, 那么第二個積分為正; 第三項恒為負; 第一個積分對應的二次型是正定的. 從而存在正常數δ2>0, 使得

由定理1和(4)知,u1,(u2-K)2,u3的導數有界, 再由引理1得

(9)

由(4)和(9)知，從存在{tm}，使得

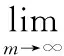
由前面的討論可知,E2(0,K,0) 局部漸近穩定. 所以, 當t→∞時,(u1(x,t),u2(x,t),u3(x,t))→(0,K,0),問題(1)的平衡點E2全局漸近穩定.

4 討 論

由以上討論知，系統 (2)有 6個平衡點E0,E1,E2,E3,E4,E5, 其中平衡點E0.E1總是不穩定點.

由定理5可知, 如果(H5)和(H7)分別成立時, 邊界平衡點E3和E4分別全局漸近穩定.

[1]Chattopadhyay J, Arino O. A predator-prey model with disease in the prey[J]. Nonlinear Anal, 1999,36(2):749-766.

[2] Xiao Y N, Chen L S． Analysis of a three species eco-epidemiological model[J]. J Math Appl, 2001, 258(2):733-754.

[3] Venturino E． The influence of diseases on Lotka-Volterra system[J]. Rlckymount J Math, 1994, 24(1)： 389-402.

[4] 趙麗萍, 李自珍, 王文婷, 馬智慧. 一類疾病垂直感染的生態—流行病模型的動力學研究[J]. 蘭州大學學報(自然科學版), 2009, 45(4): 127-132.

[5] 郭中凱, 李文龍, 程雷虎, 李自珍. 具有功能性反應且捕食者有病的生態—流行病模型[J]. 蘭州大學學報(自然科學版), 2009, 45(3): 117-121.

[6] 孫樹林, 原存德. 捕食者具有流行病的捕食—被捕食(sI)模型的分析[J]. 生物數學學報, 2006, 21(1): 97-104.

[7] Pao C V. Nonlinear Parabolic and Elliptic Equations[M]. New York: Prenum, 1992.

[8] Henry D. Geometic Theory of Semilinear Parabolic Equations[M]. New York: Springer-Verlag, 1993.

[9] 王明新．非線性拋物型方程[ M]．北京: 科學出版社, 1993. 121-122.

[10] Brown K J, Dunne P C, Gardner R A. A semilinear parabolic ststem arising in the theory of superconductivity[J]. J Diff Eqs, 1981, 40: 232-252.

【責任編輯：王軍】

Global behavior of solutions in a diffusive eco-epidemiological model with disease and vertical infection in the prey

CHEN Anning

(School of Mathematics and Statistics, Longdong University, Qingyang 745000,China)

In this paper, global behavior of solutions in a diffusive eco-epidemiological model with disease and vertical infection in the prey is discussed. Firstly, the global existence, uniqueness and uniform boundedness of positive solutions to (2) are proved under homogeneous Neumann boundary condition. Secondly, by using linearization， we obtained the sufficient condition of locally asymptotical stability of the equilibria point． Furthermore, the sufficient conditions for the extinction of infective prey population, disease disappearance and epidemic persistence were obtained through analyzing the global asymptotical stability of the equilibria point by Lyapunov function.

vertical infection; spatial diffusion; eco-epidemiological model； stability

2014-05-23

陳安寧(1965-)，男，隴東學院副教授，主要從事數學教學論及應用數學的研究.

O175.26

A

1672-3600(2015)03-0037-06