基于ICA-ELM的工業(yè)過程故障分類
嚴(yán)文武,潘 豐
(江南大學(xué)輕工過程先進控制教育部重點實驗室,江蘇 無錫 214122)
基于ICA-ELM的工業(yè)過程故障分類
嚴(yán)文武,潘 豐
(江南大學(xué)輕工過程先進控制教育部重點實驗室,江蘇 無錫 214122)
基于獨立成分分析(ICA)的多變量統(tǒng)計過程監(jiān)控主要用于故障檢測,不能有效地進行故障分類。為此,結(jié)合極限學(xué)習(xí)機(ELM),提出一種ICA-ELM的故障分類方法。利用ICA提取故障特征,通過ELM學(xué)習(xí)算法訓(xùn)練神經(jīng)網(wǎng)絡(luò),從而實現(xiàn)故障分類。采用 TE過程數(shù)據(jù)進行驗證,實驗結(jié)果表明,與概率神經(jīng)網(wǎng)絡(luò)和支持向量機相比,ICA-ELM算法的故障分類準(zhǔn)確率更高,訓(xùn)練速度更快。
獨立成分分析;極限學(xué)習(xí)機;故障分類;概率神經(jīng)網(wǎng)絡(luò);支持向量機;TE過程
DO I:10.3969/j.issn.1000-3428.2015.10.055
1 概述
為了實現(xiàn)更大的產(chǎn)能和更高的產(chǎn)品質(zhì)量,工業(yè)系統(tǒng)變得越來越復(fù)雜,隨之,現(xiàn)代工業(yè)過程監(jiān)控受到越來越多的關(guān)注。目前比較流行的過程監(jiān)控方法有多變量統(tǒng)計法、專家系統(tǒng)法和人工智能法等[1]。在多變量統(tǒng)計方法中最為普遍的是主成分分析法(Principal Component Analysis,PCA)和獨立成分分析法(Independent Component Analysis,ICA)等[2]。獨立成分分析最初是為了解決盲信號分離問題而被提出,后作為主成分分析法的延伸被引入多變量統(tǒng)計過程監(jiān)控。與PCA方法相比,ICA方法不要求變量滿足高斯分布,能夠有效地利用信號中的高階統(tǒng)計信息,提取內(nèi)在獨立特性成分,從而更有效地進行過程監(jiān)控[3]。
ICA方法故障檢測性能較好,但在故障識別分類方面有所欠缺。在工業(yè)過程故障診斷中,快速準(zhǔn)確地進行故障分類有重要的意義,及時地識別故障類型有助于盡早排除故障,恢復(fù)正常生產(chǎn)。傳統(tǒng)的智能故障分類方法有反向傳播神經(jīng)網(wǎng)絡(luò)(Back Propagation Neural Network,BPNN)、概率神經(jīng)網(wǎng)絡(luò)(Probabilistic Neural Network,PNN)等,對于小樣本分類有支持向量機(Support Vector Machine,SVM)。傳統(tǒng)神經(jīng)網(wǎng)絡(luò)訓(xùn)練時間大多過于冗長,且訓(xùn)練參數(shù)選擇復(fù)雜。支持向量機分類同樣存在參數(shù)選擇復(fù)雜的問題,且隨著訓(xùn)練數(shù)據(jù)量的增加,算法計算量急劇
增加,所需訓(xùn)練時間過長,算法甚至難以實施。為此,本文提出一種ICA-ELM算法來實現(xiàn)快速簡單的故障分類。極限學(xué)習(xí)機(Extreme Learning Machine,ELM)是一種針對單隱藏層前饋神經(jīng)網(wǎng)絡(luò)的快速機器學(xué)習(xí)算法,該算法訓(xùn)練速度快、參數(shù)簡單易于實現(xiàn),同時具有很好的范化能力[4]。本文通過TE化工過程仿真來測試ICA-ELM方法的可行性,并與PNN和SVM方法進行比較。
2 ICA和ELM理論
2.1 獨立成分分析
獨立成分分析(ICA)是信號處理領(lǐng)域在20世紀(jì)90年代后期發(fā)展起來的一項新處理方法,文獻[5]提出了基于ICA的過程監(jiān)控方法。
多導(dǎo)觀測X是多個獨立信號S通過混合矩陣A組合而成(X=AS),ICA的任務(wù)就是在S和A均未知的情況下,求解混矩陣W,使得X通過W得到的輸出Y(Y=WX)是S的最優(yōu)逼迫。
獨立成分分析算法有很多,其中快速ICA算法(FastICA)因為收斂速度快、效果好而被廣泛應(yīng)用[6]。
2.2 極限學(xué)習(xí)機
極限學(xué)習(xí)機是一種針對于單隱含層前饋神經(jīng)網(wǎng)絡(luò)(Single-hidden Layer Feedforward Neural Network,SLFN)的學(xué)習(xí)算法。由文獻[7-8]提出的極限學(xué)習(xí)機(ELM)算法克服了大多數(shù)基于梯度下降法神經(jīng)網(wǎng)絡(luò)訓(xùn)練慢、易陷入局部極小點、學(xué)習(xí)率敏感等缺點。該算法僅需設(shè)置隱含層神經(jīng)元個數(shù)便可求得唯一最優(yōu)解,整個算法一次完成,無須迭代,學(xué)習(xí)速度極快(通常是BPNN、SVM等速度10倍以上)。
ELM網(wǎng)絡(luò)結(jié)構(gòu)如圖 1所示,是一個典型的SLFN結(jié)構(gòu),由輸入層、隱含層和輸出層構(gòu)成,其神經(jīng)元數(shù)分別為n,l,m。
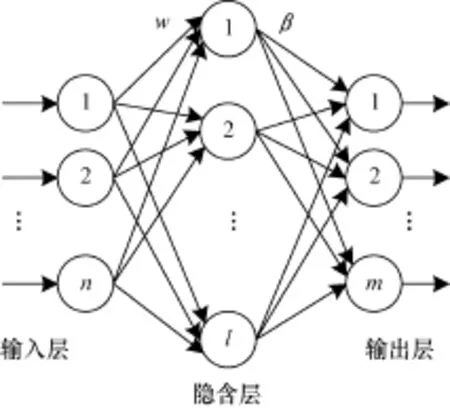
圖1 ELM網(wǎng)絡(luò)結(jié)構(gòu)
設(shè)連接隱含層的輸入連接權(quán)矩陣為 w,隱含層閾值矩陣為b,輸出權(quán)值矩陣為β,分別表示為:
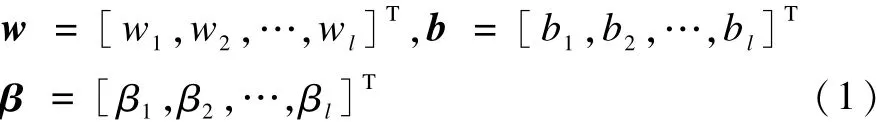
其中,wi=[wi1,wi2,…,win];βi=[βi1,βi2,…,βim]。
設(shè)有 q組輸入輸出,則輸入和輸出矩陣分別為X=[χ1,χ2,…,χQ]n×q,T=[t1,t2,…,tQ]m×q,則有:
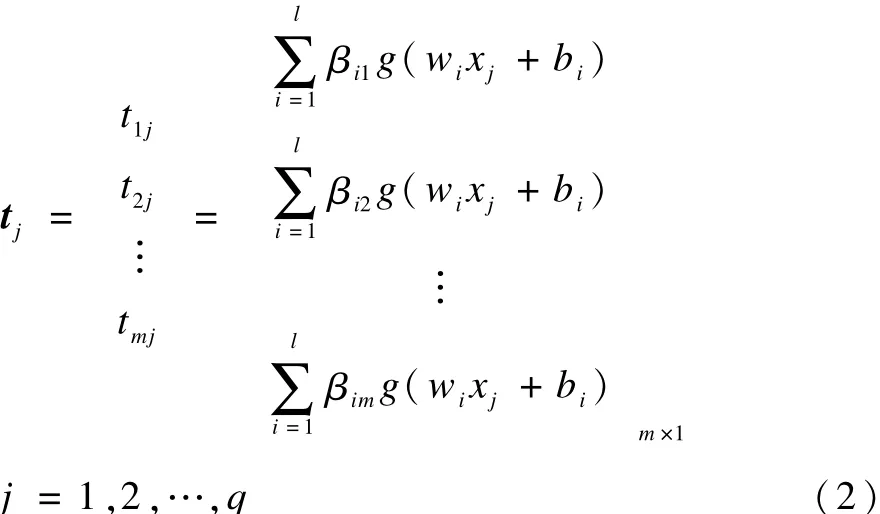
其中,χj=[χ1j,χ2j,…,χnj]T;g()為隱含層神經(jīng)元激活函數(shù)(該函數(shù)無限可微)。可將式(2)表示成如下形式:

其中,TT為T的轉(zhuǎn)置;H為神經(jīng)網(wǎng)絡(luò)的隱含層輸出矩陣,形式如下:
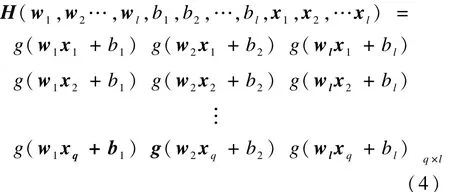
ELM算法步驟如下:
(1)確定神經(jīng)元個數(shù)。
(2)隨機選取 w和 b,并計算隱含層輸出矩陣H。
由上述算法步驟可以看出,ELM算法不需要在訓(xùn)練過程中調(diào)整 w和 b,只需設(shè)置好神經(jīng)元個數(shù),按以上算法一次性就能得到唯一全局最優(yōu)解β^,不存在會陷入局部最優(yōu)的問題。整個ELM算法參數(shù)選擇簡單,沒有迭代過程,所以算法速度得到了極大提升。
3 ICA-ELM故障分類
ICA-ELM故障分類方法,首先利用獨立成分分析提取獨立故障特征,將所提取的故障特征作為神
經(jīng)網(wǎng)絡(luò)的輸入,再通過ELM學(xué)習(xí)算法訓(xùn)練神經(jīng)網(wǎng)絡(luò),從而實現(xiàn)故障分類。
ICA-ELM故障分類主要分為4大步,依次為數(shù)據(jù)預(yù)處理、ICA建模、ELM建模和分類測試,算法流程如圖2所示。
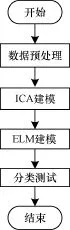
圖2 ICA-ELM故障分類
ICA-ELM具體算法如下:
(1)對所有數(shù)據(jù)作標(biāo)準(zhǔn)化處理,去均值后除標(biāo)準(zhǔn)差得到數(shù)據(jù)矩陣X。正常狀態(tài)數(shù)據(jù)Xnormal經(jīng)PCA去相關(guān)得Znormal:

其中,Q為PCA白化矩陣。
(2)對Znormal進行ICA分析,得到解混矩陣W。
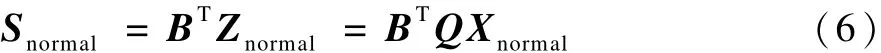
其中,Snormal為正常狀態(tài)獨立成分;B采用FastICA算法[9]求得,則有解混矩陣W=BTQ。
(3)故障數(shù)據(jù)Xfault經(jīng)W可得到故障特征Sfault= WXfault。設(shè)故障標(biāo)簽為 t=[0,0,…,1,0,0,…,0]T(即ELM網(wǎng)絡(luò)輸出),若為故障i,則對應(yīng)故障標(biāo)簽第i個元素為1,其余為0。將Sfault和故障標(biāo)簽t分別作為單隱含層神經(jīng)網(wǎng)絡(luò)的輸入和輸出,采用ELM學(xué)習(xí)算法訓(xùn)練網(wǎng)絡(luò),得到相應(yīng)網(wǎng)絡(luò)參數(shù)。
(4)進行故障分類。待分類故障數(shù)據(jù) Xtest經(jīng) W得到待分類故障特征Stest=WXtest,再由ELM網(wǎng)絡(luò)分類得到故障標(biāo)簽,從而判斷故障類型。
4 ICA-ELM實驗分析
4.1 實驗數(shù)據(jù)來源
實驗數(shù)據(jù)來自Tennessee Eastman(TE)化工過程,該過程由美國伊斯曼化學(xué)品公司過程控制部提出,被廣泛應(yīng)用于連續(xù)過程的監(jiān)視診斷研究。
TE過程包括41個測量變量和12個控制變量,預(yù)設(shè)有21個故障,具體見文獻[10]。該實驗選取前16個測量變量進行過程監(jiān)控,并取正常狀態(tài)和故障1,2,6,8,13,14數(shù)據(jù)作為實驗數(shù)據(jù)。這6種故障的描述如表1所示。

表1 TE中的6種故障描述
4.2 ICA特征提取
從TE過程數(shù)據(jù)中選取前16個監(jiān)控量進行ICA建模。首先對正常狀態(tài)數(shù)據(jù)進行預(yù)處理,標(biāo)準(zhǔn)化得到 Xnormal,后用 PCA去相關(guān)化得到 Znormal,再使用FastICA算法求得解混矩陣W,最后得到正常狀態(tài)獨立成分Snormal=WXnormal。故障數(shù)據(jù)Xfault通過W可得故障狀態(tài)獨立成分Sfault=WXfault。將Sfault故障狀態(tài)特征數(shù)據(jù)結(jié)合ELM算法實現(xiàn)故障分類。
ICA特征提取采用500組TE正常狀態(tài)數(shù)據(jù)用于求得分離矩陣W。所選6種TE故障數(shù)據(jù)分為訓(xùn)練集和測試集,其中訓(xùn)練集每種故障有480組數(shù)據(jù),測試集每種故障數(shù)據(jù)有800組數(shù)據(jù)。由此,可提取到故障訓(xùn)練集和測試集特征數(shù)據(jù),分別記為 Sf-train和Sf-test。
4.3 ICA-ELM模型
為了實現(xiàn)ELM分類功能,給每類故障定義一個故障標(biāo)簽作為神經(jīng)網(wǎng)的輸出值t。設(shè)第i類故障標(biāo)簽為[0,0,…,1,0,0,…,0]T,該向量第 i個元素為 1,其余均為0。
ELM算法唯一需要確定的參數(shù)是神經(jīng)元的個數(shù),理論上神經(jīng)元個數(shù)等于訓(xùn)練樣本個數(shù)時,ELM網(wǎng)絡(luò)可零誤差逼近訓(xùn)練樣本。在實際應(yīng)用中,出于減少計算量和實際效果考慮,神經(jīng)元個數(shù)都遠小于樣本數(shù)。
為了分析ELM隱含層神經(jīng)元個數(shù)l對實際分類效果的影響,令l=100,110,120,…,1 000(一次增加10),分別進行10次測試,其中,ELM訓(xùn)練集和測試集分別為Sf-train和Sf-test,網(wǎng)絡(luò)激活函數(shù)采用常用的S型函數(shù)為:

分析結(jié)果如圖3所示,l值越大,訓(xùn)練集分類正確率越高,但測試集分類效果并非l越大越好。l= 450時,效果最好。因此,ELM需要在訓(xùn)練集和測試
集正確率間折中選擇合適的隱含層神經(jīng)元個數(shù)l。
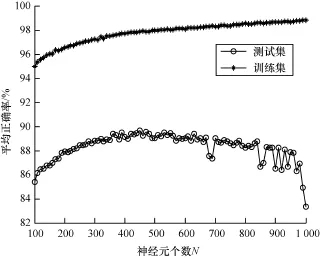
圖3 神經(jīng)元個數(shù)對分類結(jié)果的影響
ICA-ELM模型整體流程如下:
(1)TE正常狀態(tài)原始數(shù)據(jù)經(jīng)標(biāo)準(zhǔn)化和PCA去相關(guān)化得到Znormal。
(2)Znormal經(jīng)FastICA算法求得解混矩陣W。
(3)提取故障特征數(shù)據(jù),得到訓(xùn)練集數(shù)據(jù) Sf-train和測試集數(shù)據(jù)Sf-test,并在ELM網(wǎng)絡(luò)訓(xùn)練之前作歸一化處理。
(4)確定ELM神經(jīng)元個數(shù)l=450。
(5)設(shè)ELM激活函數(shù)為g(χ)=1/(1+e-χ),隨機選取輸入層與隱含層連接權(quán)w和隱含層神經(jīng)元閥值b,選定后不改變。
(7)測試集通過所得網(wǎng)絡(luò)可求得對應(yīng)輸出t,由t可知故障類別數(shù)。
4.4 ICA-ELM分類效果
通過結(jié)合ELM算法,彌補了基于ICA多變量統(tǒng)計過程監(jiān)控在故障分類方面的不足。ICA-ELM實際分類效果如圖4所示。ICA-ELM故障分類正確率接近90%,效果較為理想。
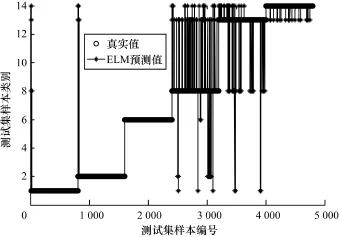
圖4 ICA-ELM分類結(jié)果
5 算法分類效果與性能比較
除了ICA-ELM方法進行故障分類外,其他方法也可實現(xiàn)故障分類的目的,比如ICA可結(jié)合概率神經(jīng)網(wǎng)絡(luò)(PNN)和支持向量機(SVM),這3種方法分類效果如表2所示。
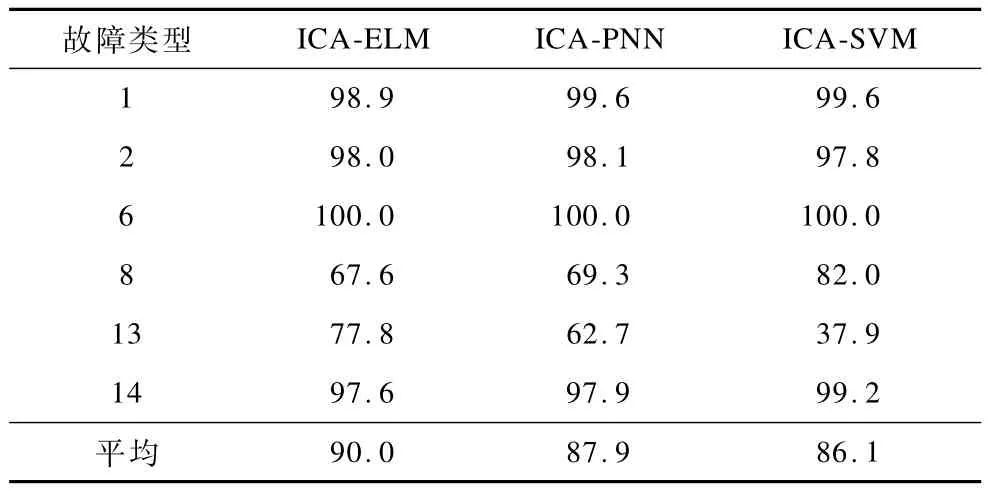
表2 測試集分類效果 %
從表2可以看出,ICA-ELM,ICA-PNN和ICA-SVM這3種方法都能夠有效地進行故障分類。其中,結(jié)合ELM方法的分類效果最好,平均分類正確率最高,達到90.0%。對于階躍類型和閥粘滯型的故障,如故障1、故障2、故障6和故障14,3種方法都有97%以上的分類正確率。對于隨機變量型的故障8,結(jié)合SVM方法的效果較好,這是由于SVM對于不易區(qū)分的類別(如故障8和故障13)有所偏重,故障8分類正確率高,而故障13分類正確率低,其中故障13更多地被錯誤歸類為故障8。對于慢偏移型的故障13,結(jié)合ELM方法的效果較好。
表3為3種算法的分析。ELM算法結(jié)構(gòu)簡單,參數(shù)選擇方便,無需迭代學(xué)習(xí),所以故障訓(xùn)練和測試時間用時少,3種算法中最快。PNN算法是一種結(jié)合概率密度分類估計的并行處理神經(jīng)網(wǎng)絡(luò)[11],具有快速學(xué)習(xí)能力,PNN算法比ELM速度稍慢,速度也很快。PNN算法中隱含層神經(jīng)元個數(shù)等于樣本個數(shù),而ELM神經(jīng)元個數(shù)一般都遠小于樣本數(shù)。PNN樣本個數(shù)越多,隱含層神經(jīng)元個數(shù)越多,網(wǎng)絡(luò)的逼近精度就越高,但也將導(dǎo)致網(wǎng)絡(luò)復(fù)雜度隨之提高。SVM算法參數(shù)較多,合理地選擇參數(shù)對分類效果有重要的作用,為了確定這些參數(shù)以達到理想的分類效果,需要花費大量時間[12]。
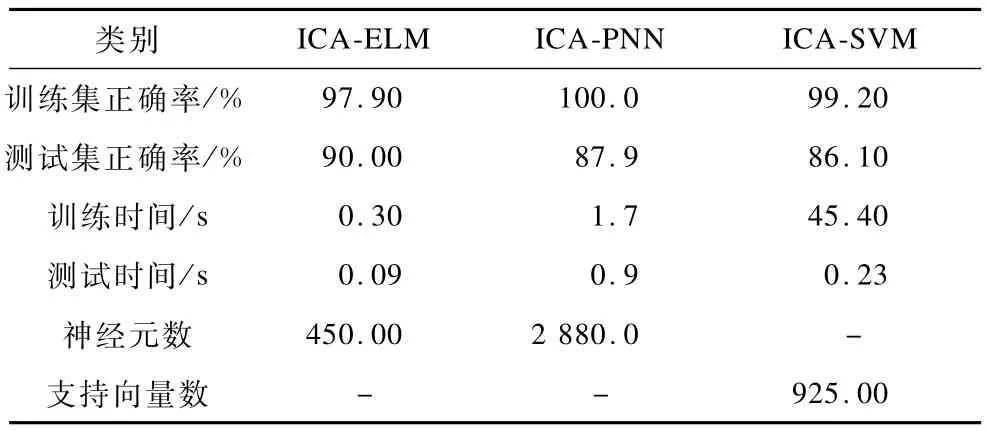
表3 3種算法性能比較
6 結(jié)束語
本文提出一種將獨立成分分析與極限學(xué)習(xí)機相結(jié)合的工業(yè)過程故障分類方法。利用ICA的故障提取能力和ELM的快速學(xué)習(xí)能力實現(xiàn)故障的快速分類。通過TE故障數(shù)據(jù)進行實驗,結(jié)果表明,ICAELM方法分類效果和速度都較好,結(jié)構(gòu)簡單且參數(shù)選擇方便,唯一參數(shù)隱含層神經(jīng)元個數(shù)對分類效果有一定的可控性。但ICA-ELM方法仍有一定的改進空間。本文算法主要是針對線性獨立成分分析,可以考慮采用非線性獨立成分分析的方法來提取故障特征。本文ELM算法為離線固定型,當(dāng)建模完成后,不能根據(jù)新的數(shù)據(jù)更新模型,可使用可在線更新的ELM算法。
[1] 李 晗,蕭德云.基于數(shù)據(jù)驅(qū)動的故障診斷方法綜述[J].控制與決策,2011,26(1):1-9.
[2] 周東華,李 鋼,李 元.數(shù)據(jù)驅(qū)動的工業(yè)過程故障診斷技術(shù)——基于主元分析與偏最小二乘的方法[M].北京:科學(xué)出版社,2011.
[3] 樊繼聰,王友清,秦泗釗.聯(lián)合指標(biāo)獨立成分分析在多變量過程故障診斷中的應(yīng)用[J].自動化學(xué)報,2013,39(5):494-501.
[4] 鄧萬宇,鄭慶華,陳 琳,等.神經(jīng)網(wǎng)絡(luò)極速學(xué)習(xí)方法研究[J].計算機學(xué)報,2010,33(2):279-287.
[5] Kano M,Tanaka S,Hasebe S,et al.Monitoring Independent Components for Fault Detection[J].AIChE Journal,2003,49(4):969-976.
[6] 張 杰,劉 輝,歐倫偉.改進的FastICA算法研究[J].計算機工程與應(yīng)用,2014,50(6):210-218.
[7] Huang Guangbin,Zhu Qinyu,Siew C K.Extreme Learning Machine:A New Learning Scheme of Feed Forward Neural Networks[C]//Proceedings of IEEE International Joint Conference on Neural Networks. Washington D.C.,USA:IEEE Press,2004:985-990.
[8] Huang Guangbin,Zhu Qinyu,Siew C K.Extreme Learning Machine:Theory and Applications[J].Neurocomputing,2006,70(1):489-501.
[9] Hyv?rinen A,Oja E.Independent Component Analysis:Algorithm s and Applications[J].Neural Networks,2000,13(4):411-430.
[10] Chiang L H,Braatz R D,Russell E L.Fault Detection and Diagnosis in Industrial Systems[M].Berlin,Germany:Springer,2001.
[11] 繆素云,張 峰,李 蕊,等.基于概率神經(jīng)網(wǎng)絡(luò)的 TE過程故障診斷[J].自動化技術(shù)與應(yīng)用,2011,30(5):78-80.
[12] 丁 勇,秦曉明,何寒暉.支持向量機的參數(shù)優(yōu)化及其文本分類中的應(yīng)用[J].計算機仿真,2010,27(11):187-190.
編輯顧逸斐
Industry Process Fault Classification Based on ICA-ELM
YAN Wenwu,PAN Feng
(Key Laboratory of Advanced Control for Light Industry Process,Ministry of Education,Jiangnan University,Wuxi 214122,China)
The process monitoring method with multivariate statistics based on Independent Component Analysis(ICA)is mainly used for fault detection,but it is not effective for fault classification.For this reason,combining with Extreme Learning Machine(ELM),a method called ICA-ELM for fault classification is proposed.ICA-ELM extracts the fault features with ICA,and then trains the networks with ELM,so as to realize fault classification.ICA-ELM is tested with Tennessee Eastman(TE)process data and compared with Probabilistic Neural Network(PNN)and Support Vector Machine(SVM).Experimental result show s that the accuracy of ICA-ELM is higher,training speed of ICA-ELM is faster.
Independent Component Analysis(ICA);Extreme Learning Machine(ELM);fault classification;Probabilistic Neural Network(PNN);Support Vector Machine(SVM);Tennessee Eastman(TE)process
嚴(yán)文武,潘 豐.基于ICA-ELM的工業(yè)過程故障分類[J].計算機工程,2015,41(10):290-294.
英文引用格式:Yan Wenwu,Pan Feng.Industry Process Fault Classification Based on ICA-ELM[J].Computer Engineering,2015,41(10):290-294.
1000-3428(2015)10-0290-05
A
TP39
國家自然科學(xué)基金資助項目(61273131);江蘇省產(chǎn)學(xué)研聯(lián)合創(chuàng)新基金資助項目(BY 2013015-39)。
嚴(yán)文武(1989-),男,碩士研究生,主研方向:控制理論與控制工程;潘 豐,教授、博士生導(dǎo)師。
2014-09-30
2014-11-03E-mail:yanw enwu1989@outlook.com

