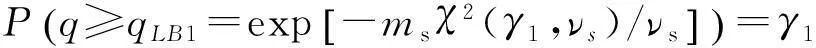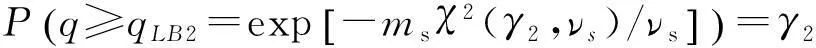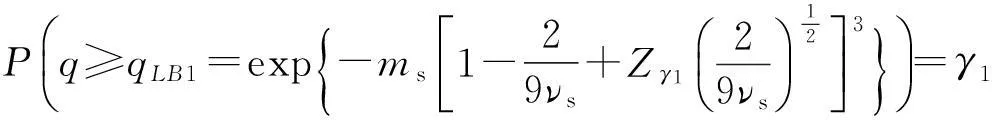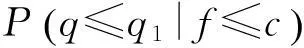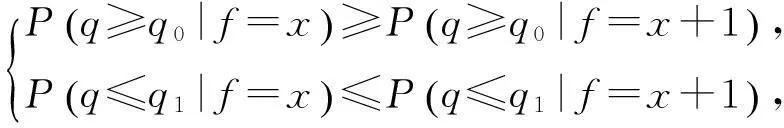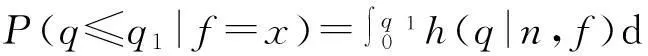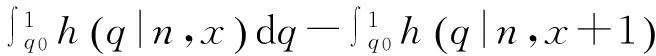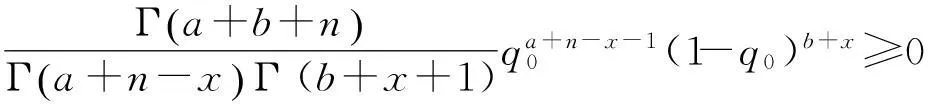利用分系統數據制定整機測試性驗證試驗方案*1

?

利用分系統數據制定整機測試性驗證試驗方案*1

王敏，楊江平，盧雷，王永攀

(空軍預警學院，湖北 武漢430019)

摘要：現有利用研制階段試驗數據制定測試性驗證試驗方案的方法都需要裝備整機系統測試性先驗信息，這對僅有分系統試驗信息的大型復雜裝備難以適用。針對這一問題，以故障檢測率為驗證指標，提出利用研制階段分系統試驗數據制定整機測試性驗證試驗方案的新方法。首先，利用分系統試驗數據計算整機系統故障檢測率置信下限，然后利用兩點分位數方法確定整機故障檢測率的先驗分布參數，在此基礎上根據貝葉斯最大后驗風險準則確定了新的測試性驗證試驗方案。實例對比分析表明，與傳統試驗方案相比，新方案可明顯降低試驗故障樣本量。

關鍵詞：測試性；驗證試驗方案；分系統試驗信息；故障樣本量；故障檢測率；貝葉斯方法

0引言

在裝備投入使用前，為了判定是否達到了規定的測試性要求，需進行測試性驗證試驗。測試性驗證試驗應首先確定試驗故障樣本量及允許的最大故障檢測或隔離失敗數，即測試性驗證試驗方案[1]。

現有測試性驗證試驗方案一般依據一些軍用標準來制定[2-3]。文獻[4]對比分析了二項分布模型、泊松分布模型、正態分布模型以及多項分布模型的優缺點和適用性，得出二項分布模型和泊松分布模型在確定測試性驗證試驗方案上具有明顯的優勢。文獻[5]通過對二項分布函數單調性的討論，提出了求解二項分布函數聯立不等式的精確算法，可迅速準確地獲得測試性驗證的抽樣方案。文獻[6-7]分析了國內外現有軍用標準中給出的測試性驗證方法，總結出現有方法存在普遍適用性缺乏、可操作性差等不足之處，提出應該制定測試性驗證專用標準。以上標準與方法中關于驗證試驗方案的確定是在對裝備測試性水平完全未知的情況下確定的，往往具有試驗樣本量大、試驗周期長、費用高等缺點，在工程上難以實現。為此，國內外學者開始關注如何利用驗證試驗前的先驗信息來制定測試性驗證試驗方案，進而減少試驗故障樣本量，節省試驗費用。文獻[8-9]將研制階段的試驗數據進行折合，得到驗證試驗前故障檢測率(fault detection rate, FDR)的信仰(fiducial)分布，依據此分布制定了FDR的驗證試驗方案。由于利用了研制階段的試驗數據，得到的試驗方案相比于二項分布法，樣本量減少效果明顯，但沒有考慮研制過程中多階段的試驗數據來自不同總體的特點。文獻[10]運用證據理論方法，建立了基于融合不同種類研制信息(測試性試驗數據、測試性預計結果和專家經驗)的測試性驗證試驗方案。文獻[11]提出利用研制階段試驗數據和專家信息制定測試性驗證試驗方案的貝葉斯方法。該方法首先利用研制階段試驗數據建立了產品的FDR增長模型，以此描述FDR在研制階段的變化趨勢，然后利用專家信息確定模型中的超參數，進而得到FDR的驗前分布，最后依據貝葉斯最大后驗風險準則制定了新的測試性驗證試驗方案。

上述研究利用的先驗信息都是整機系統自身的歷史試驗數據，而對于設備量大或體積龐大的裝備，如大型復雜電子裝備，由于系統復雜，試驗組織困難，試驗費用高昂，研制過程中整機系統自身的試驗較少甚至沒有，因此，上述研究在制定大型復雜裝備測試性驗證試驗方案上適用性不強。在實際工程中，為保證整機系統的測試性水平，構成整機系統的分系統通常會有較多的試驗數據，通過這些數據可以確定整機系統的測試性先驗水平。基于文獻[12]，根據將分系統試驗數據融合到可靠性驗證中的思想，本文以整機系統故障檢測率FDR為驗證指標，討論了二項分布下，利用分系統試驗數據制定整機系統測試性驗證試驗方案的新方法。本文方法適用于整機測試性先驗信息缺乏的情況，依據本文方法確定的測試性驗證試驗方案，可有效減少故障樣本量，節省試驗費用。

1FDR一次抽樣試驗方案

FDR的驗證試驗可以看成是成敗型試驗。典型的FDR一次抽樣試驗方案的思路是：隨機抽取n個故障樣本進行試驗，其中有f次沒檢測到故障(檢測失敗)。規定一個正整數c，如果f≤c則認為FDR合格，判定接收；如果f>c則認為不合格，判定拒收。試驗方案簡記為(n，c)。

設裝備整機系統的FDR為q，則在n次試驗中，出現f次失敗的概率為

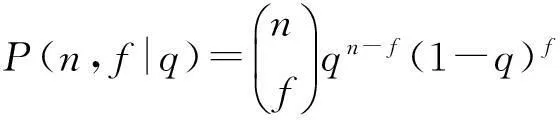
(1)

產品被接收的概率，即f≤c的概率為

(2)

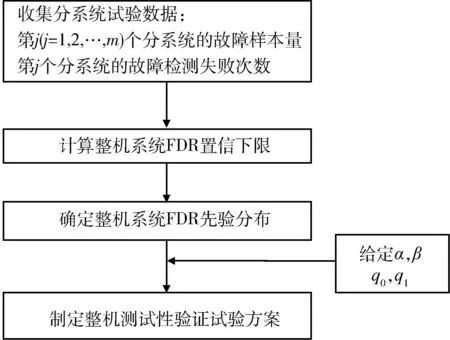
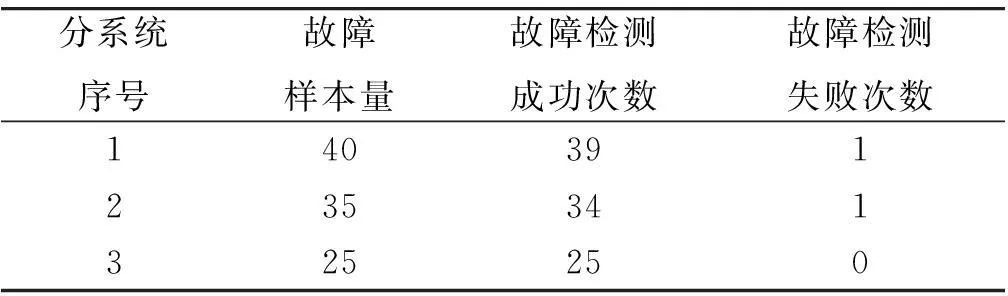
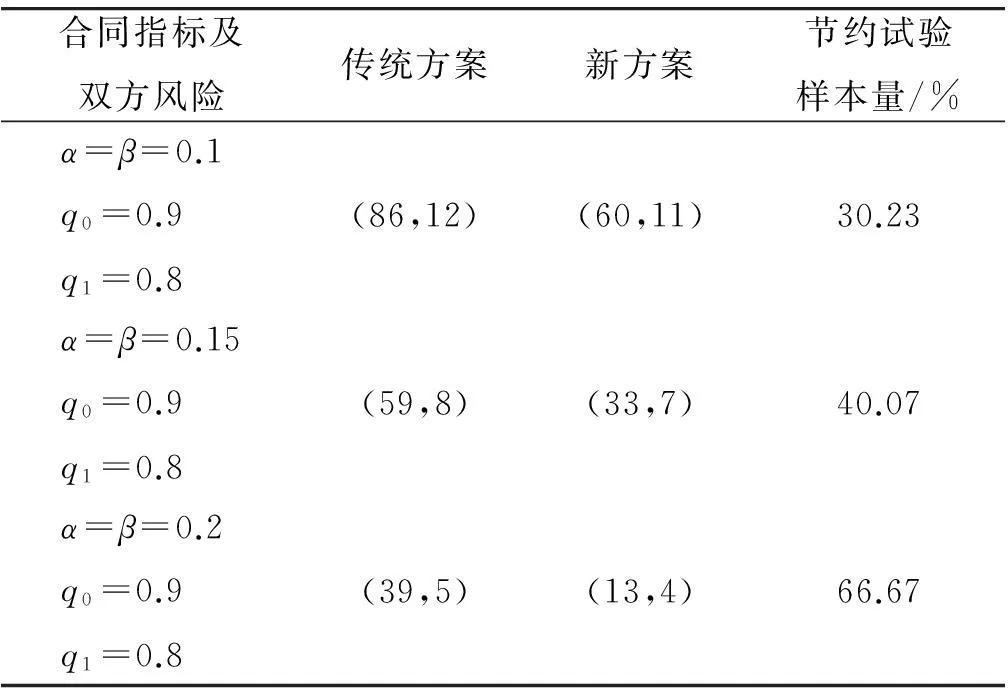
裝備在設計之初，使用方和生產方協商確定FDR的設計要求值q0(規定值)和最低可接受值q1，且q1

(3)

對于FDR要求較高的裝備，若雙方要求風險較低，則依據式(3)確定的故障樣本量很大。例如，對于大型相控陣雷達，如果規定q0=0.95,q1=0.90，α=β=0.05，則可確定試驗方案為(298,21)。由于故障注入試驗的破壞性，在裝備中注入大量的故障是不現實的。因此，上述試驗方案在工程中很難以實現。

2利用分系統數據制定整機測試性驗證試驗方案的方法

2.1方法流程

新方法的流程如圖1所示：首先利用分系統試驗數據計算整機系統FDR置信下限，然后采用兩點分位數方法確定整機系統FDR的Beta先驗分布參數，最后在給定α，β，q0，q1情況下，依據貝葉斯最大后驗風險準則制定整機系統FDR的驗證試驗方案。

圖1　方法流程圖Fig.1　Flow chart of the method

2.2計算整機故障檢測率置信下限

考慮由m個分系統組成的串聯整機系統，設各分系統故障發生相互獨立，第j(j=1,2,…,m)個分系統在進行測試性驗證試驗時，注入故障樣本量為nj，其中有xj次故障檢測失敗。利用近似最優法求取整機系統FDR的置信下限[10]，計算公式如下：

當νs<3時，

(4)

(5)

當νs≥3時，

(6)

(7)

(8)

νs=4ms/Δ，

(9)

(10)

(11)

2.3確定整機故障檢測率先驗分布

系統FDR的先驗分布類型，國內外文獻大多選取Beta(a，b)分布，其密度函數可表示為

(12)

確定整機系統FDR的先驗分布參數，可給定2個不同的置信水平，由式(4)，(5)或式(6)，(7)分別求出其對應的單側置信下限，進而利用兩點分位數方法確定先驗分布的參數，如下所示：

(13)

用Matlab軟件編制程序可求解出參數a和b,進而得到整機FDR的先驗分布。

2.4確定整機系統測試性驗證試驗方案

在獲得整機FDR先驗分布后，即可制定相應測試性驗證試驗方案。假設使用方和生產方協商確定的試驗方案為(n，c)，現場驗證試驗結果為(n，f)，f表示故障檢測失敗次數，則整機故障檢測率FDR的后驗分布為

(14)

即q的后驗分布為Beta(a+n-f，b+f)分布。

根據式(14)可證明如下不等式組成立：

(15)

上述不等式組中2個不等式證明類似，下面證明第1個不等式：

maxP(q≤q1|f≤c)=P(q≤q1|f=c).

(16)

(17)

若規定使用方風險為β，生產方風險為α，則可由下列不等式組制定新的試驗方案(n，c)。

(18)

3實例分析

某電子設備由3個分系統串聯而成，在研制過程中分別對各分系統進行測試性試驗。各分系統試驗數據見表1。

表1　各分系統試驗數據

對表1中分系統試驗數據進行折合，可得出整機故障檢測率的Beta先驗分布參數a=25，b=2。在求得先驗分布后，就可制定整機可靠度新試驗方案。

為了對比分析傳統一次抽樣試驗方案和新試驗方案的優劣，選取3組不同的合同指標及風險組合，對比分析結果見表2。

表2　傳統試驗方案和新試驗方案的結果對比

由表2的對比分析結果可以看出，整機故障檢測率新試驗方案由于考慮了分系統的試驗信息，相比傳統試驗方案具有以下優點：

(1) 在雙方風險相同的情況下，新試驗方案可明顯減少試驗樣本。例如在第1種組合情況下，試驗故障樣本量可節約30.23%。

(2) 由于需注入的故障樣本量少，新試驗方案可操作性更強。

4結束語

本文方法可以充分利用裝備研制階段分系統的測試性試驗信息，對于整機系統測試性先驗信息缺乏的情況尤為適用。

采用本文方法制定的整機測試性驗證試驗方案較傳統一次抽樣方案試驗所需故障樣本量大為降低，可節約試驗經費。

參考文獻：

[1]田仲,石君友.系統測試性設計分析與驗證[M].北京:北京航空航天大學出版社,2003.

TIAN Zhong, SHI Jun-you. Design, Analysis and Demonstration of System Testability [M]. Beijing: Beihang University Press, 2003.

[2]Department of Defense Washington D C. MIL- STD-471A: Maintainability Verification/Demonstration/Evaluation [S]. U. S Government Printing Office, 1973.

[3]國防科學技術工業委員會.GJB 2072-94 維修性試驗與評定[S].北京:中國標準出版社,1994.

National Science and Technology Industrial Committee. GJB 2072-94 Maintainability Test and Evaluation[S].Beijing: Standards Press of China.1994.

[4]田仲, 石君友.現有測試性驗證方法分析與建議[J].質量與可靠性,2006,21(2):47-51.

TIAN Zhong, SHI Jun-you Analysis and Advice for the Existing Testability Demonstration Methods [J].Quality and Reliability, 2006, 21(2):47-51.

[5]徐忠偉,周玉芬,徐松濤,等.測試性驗證中的精確算法及應用[J].航空學報,2000,21(1):67-69.

XU Zhong-wei, ZHOU Yu-fen, XU Song-tao,et al. Accurate Algorithm of Sampling Plan and Its Application in Testability Demonstration[J].Acta Aeronautica et Astronautica Sinica, 2000, 21(2): 67-69.

[6]周玉芬,徐松濤,高錫俊,等.測試性驗證的理論和方法[J].電子產品可靠性與環境試驗,1998,19(2):10-15.

ZHOU Yu-fen, XU Song-tao, GAO Xi-jun, et al.Research on Theory and Method of Testbility Demonstration Test [J].Electronic Product Reliability and Environment Testing, 1998, 19(2):10-15.

[7]石君友,紀超,李海偉.測試性驗證技術與應用現狀分析[J].測控技術,2012,31(5):29-32.

SHI Jun-you，JI Chao，LI Hai-wei. Analysis of Testability Verification Technology and Application Status [J].Measurement and Control Technology, 2012, 31(5):29-32.

[8]李天梅，邱靜，劉冠軍.利用研制階段試驗數據制定測試驗證試驗方案新方法[J].機械工程學報,2009,45(8):52-57.

LI Tian-mei, QIU Jing, LIU Guan-jun.New Methodology for Determining Testability Integrated Teat Scheme with Test Data in the Development Stages [J].Journal of Mechanical Engineering, 2009, 45(8): 52-57.

[9]李天梅，邱靜，劉冠軍. 基于Bayes變動統計理論的測試性外場統計驗證方法[J]. 航空學報,2010,31(2):335-341.

LI Tian-mei, QIU Jing, LIU Guan-jun.Research on Testability Field Statistics Verification Based on Bayes Inference Theory of Dynamic Population[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2):335-341.

[10]常春賀,楊江平,曹鵬舉.基于研制信息的測試性驗證試驗方案研究[J].航空學報,2012,33(11): 2057-2064.

CHANG Chun-he, YANG Jiang-ping, CAO Peng-ju. Study on the Scheme of Testability Demonstration Test Based on Development Information[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2057-2064.

[11]雷華軍,秦開宇.確定測試性驗證試驗方案的貝葉斯方法[J].系統工程與電子技術,2012,34(12):2612-2616.

LEI Hua-jun, QIN Kai-yu. Bayesian Method for Determination of Testability Demonstration Test Scheme [J]. Systems Engineering and Electronic, 2012, 34(12):2612-2616.

[12]Nancy R Mann. Approximately Optimum Confidence Bounds on Series and Parallel-System Reliability for Systems with Binomial Subsystem Data [J].IEEE Transactions on Reliability, 1974, 23(5): 295-304.

Determining Testability Demonstration Test Scheme with Subsystem Data

WANG Min，YANG Jiang-ping，LU Lei，WANG Yong-pan

(Air Force Early Warning Academy,Hubei Wuhan 430019, China)

Abstract:Existing method using development stage test data to determine testability demonstration test scheme needs whole system prior information, and is difficult to apply when only subsystem data are available. To solve this problem, taking the system failure detection rate as a target, a new method is presented to make full use of the subsystem test data. Firstly, the subsystem test data is used to calculate the confidence bound of system failure detection rate. Then, the two percentile method is applied to determine the prior distribution of system failure detection rate. Finally, a new testability demonstration test scheme is defined according to the Bayesian maximum posterior risk rule. Compared with the classical test scheme, the new scheme can obviously reduce the failure sample size.

Key words:testability; demonstration test scheme; subsystem test data; fault sample size; fault detection rate; Bayesian method

中圖分類號：TJ06

文獻標志碼：A

文章編號：1009-086X(2015)-05-0213-05

doi:10.3969/j.issn.1009-086x.2015.05.034

通信地址：430019湖北省武漢市黃浦大街288號研究生管理大隊20隊E-mail：lyanmin87@163.com

作者簡介：王敏(1987-)，女，山東萊蕪人。博士生，主要研究方向為預警裝備管理與保障。

*收稿日期：2014-06-18；修回日期：2014-08-23