基于最大功效檢驗判斷散落數據的歸屬*

2015-03-09 14:33:42中山大學公共衛生學院醫學統計與流行病學系510080張晉昕

中國衛生統計 2015年4期

中山大學公共衛生學院醫學統計與流行病學系（510080）趙志張晉昕

基于最大功效檢驗判斷散落數據的歸屬*

中山大學公共衛生學院醫學統計與流行病學系（510080）趙志張晉昕△

目的給出醫學研究中進行資料匯總時判斷散落資料歸屬的方法。方法按照最大功效檢驗的思想，從Neyman-Pearson引理出發，推導出遺漏資料歸屬假設檢驗的拒絕域，據以得出判斷結果的P值，全部計算在SAS環境中實現。結果此處給出的方法在分析文中的實例時，檢驗功效為0．9956，獲得的歸屬判斷結果甚為可靠。結論實際工作中出現一份資料從總體中散落，不宜直接通過差異性假設檢驗判別其歸屬，需用此處給出的假設檢驗方法合理地進行歸并。

資料歸屬 Neyman-Pearson引理最大功效檢驗

在臨床試驗［1－2］、社會調查［3］等研究實踐中，錄入數據資料時，有時會出現遺漏的情況。例如整理兩組人群資料，對A、B兩組資料分批錄入。但是隨后發現遺漏的部分資料還未錄入，而此時已經難以分辨出這部分資料屬于A、B兩組中的哪一組，僅僅知道的是，這些遺漏的資料同屬于A組或同屬于B組。

試圖將這些資料歸并回所屬組別，一種比較容易想到的做法是：根據所研究的指標，將那些遺漏的資料數據分別與兩組資料數據進行t檢驗，得到兩個P值，設其中只有一個P＞0．05，另一個P＜0．05，于是自然地將資料歸為沒有統計學意義（P＞0．05）的那組。但是，當研究的兩組人群指標差異不是很大時，兩次檢驗都會沒有統計學意義；或者當兩組人群指標差異大，兩次t檢驗都得出P＜0．05的結果。此時，若是直接比較兩個P值，將遺漏的資料歸為P值較大的那組，其判斷結果并不能令人信服。按照統計學假設檢驗的思維，為了較好控制決策所犯錯誤的大小，應通過一次假設檢驗推斷出結論。Neyman-Pearson引理為解決此問題提供了思路。

最大功效檢驗［4］

在進行假設檢驗時，無論是決定接受還是拒絕原假設，研究者都可能犯錯誤。通常，要用犯錯誤的概率來評價和比較假設檢驗方法的優劣。也就是如何控制這些犯錯誤的概率，使得在某些情況下，所選檢驗具有最小的犯錯誤概率。

一般的做法是控制犯Ⅰ類錯誤的概率，例如水平為α的檢驗對所有可能的待檢驗參數θ∈Θ0，允許犯Ⅰ類錯誤的概率至多為α。在這樣的一類檢驗中，一個好的檢驗犯Ⅱ類錯誤的概率也應當小，即當θ∈Θc0時它的功效比較大。如果一個檢驗犯Ⅱ類錯誤的概率比這類檢驗中所有其他檢驗都小，它理應是這個類中首選的檢驗。這便是最大功效檢驗（most powerful test，簡稱MP檢驗）。

對于一個需要進行假設檢驗的實際問題，想要得到最大功效檢驗并不容易。下面的定理清楚地描述了原假設和備擇假設都只含一個關于樣本的概率分布（即H0和H1都是簡單假設）的情況下，如何得到一個MP檢驗。

定理（Neyman-Pearson引理）考慮檢驗H0：θ＝θ0對H1：θ＝θ1，對于一個樣本x＝（x1，x2，…，xn），相應于θi的聯合概率密度函數或概率質量函數是f（x｜θi），i＝0，1，利用一個拒絕域為R的檢驗，R滿足對某個k≥0

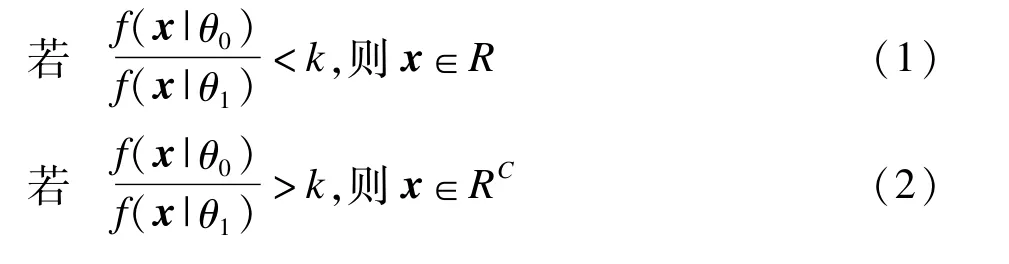
而且

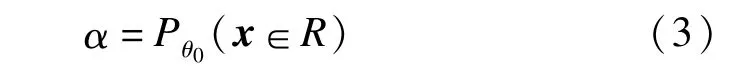
則滿足以上條件的檢驗是一個MP檢驗。

遺漏數據的假設檢驗實施

針對兩組人群遺漏資料的歸類，通過Neyman-Pearson引理做出的檢驗是很直觀的：假設研究者關心的統計指標是均值，則判別遺漏數據歸屬時，可以借助遺漏部分算出的均值與兩組總體均值的關系來推斷。建立假設時，可以直接將H0和H1分別設為：遺漏數據所對應的總體均值等于A組的總體均值以及等于B組的總體均值。這樣的檢驗結果要么是拒絕原假設，即遺漏數據來源于B組；要么不能夠拒絕原假設，即沒有充分理由否定遺漏數據來源于A組。此時，一定能給出一個判別的結果。而且，通過Neyman-Pearson引理得到的檢驗還是最大功效的檢驗，保證了判別結果的可靠性。

將所要研究的問題抽象出來：現有兩組A、B服從正態分布的獨立樣本資料m份和n份

其中，u1－α為標準正態分布的1－α分位數。因此，得到水平為α下MP檢驗的拒絕域為

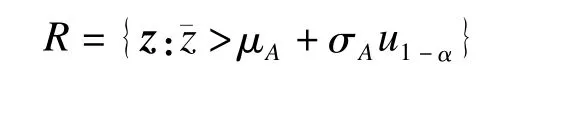
（2）當a＞0，即σ2A＜σ2B時，由式（6）得

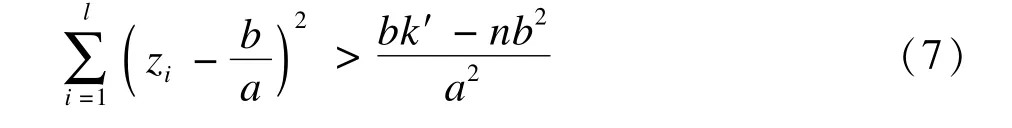
這里需要注意的是，在代入數據計算時，需要將遺漏的數據與A組數據合并后求μA和這是由于以上推導出來的拒絕域是在原假設H0成立的條件下得到的。也就是說，此時，遺漏的資料來自A組已被視作計算的前提。

舉例

某一次調查擬了解兩個民族的肺活量水平。A、B民族的肺活量數據如表1所示。研究結束后，發現有12份調查表資料未被錄入數據庫，肺活量數據為2．65，2．78，2．79，2．85，2．88，3．14，2．98，2．99，3．05，3．08，3．15，3．22。可以確知的是這12名個體屬于同一民族，可否根據統計學知識判斷他們屬于哪一個民族？

表1 兩個民族人群的肺活量／L

由以上數據計算得到：

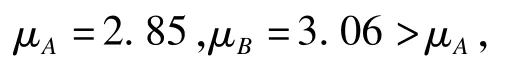
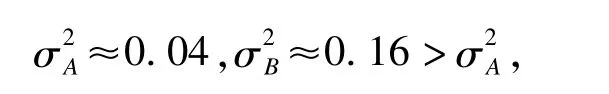
按照本文“遺漏數據的假設檢驗實施”第（2）部分內容建立假設并求得

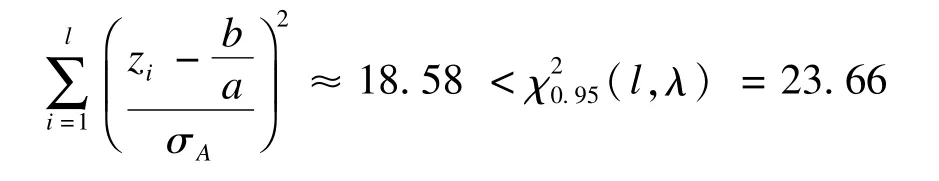
進一步通過SAS程序（見附錄）得到檢驗的P值為0．17，也就是說，在顯著性水平α＝0．05時，不能夠拒絕原假設，即遺漏資料屬于A民族。同時，可以計算出檢驗功效為0．9956，提示結論較可靠。

討論

實際調查研究中，簡單的兩組人群資料獨立錄入結束后，遺漏的部分可以通過數理統計中的Neyman-Pearson引理將其合理地判給所屬的資料組別。并且，由于對應的檢驗是MP檢驗，故能夠在控制Ⅰ類錯誤的前提下，使得犯Ⅱ類錯誤的概率最小，為實際工作判別資料的歸屬提供了切實有效的方法。

另外，如果出現多組資料錄入后，遺漏了部分資料，本文所述方法尚不能夠奏效。此時可以嘗試通過判別分析或者其他一些算法分類器，如樸素貝葉斯（naive Bayes classifier）、支持向量機（support vector machines）等判斷資料的歸屬情況，但是這些方法都不能像假設檢驗那樣，在作出決策的同時控制犯錯誤的概率水平。

［1］O′Leary E，Seow H，Julian J，et al．Data collection in cancer clinical trials：Too much of a good thing．Clinical Trials，2013，10（4）：624-632．

［2］范彩霞，吳劍秋，寇瑩瑩，等．RDC Onsite-藥物臨床試驗數據采集系統電子病例報告表常見疑問分析．藥學與臨床研究，2013，21（2）：196-198．

［3］陳向明．資料的歸類和分析．社會科學戰線，1999，4：223-229．

［4］Casella G，Berger R L．統計推斷．第2版．張忠占，傅鶯鶯譯．北京：機械工業出版社，2010，356-358．

［5］韋博成．參數統計教程．北京：高等教育出版社，2006，18-20．

附錄 SAS假設檢驗P值和功效計算程序