復(fù)雜抽樣數(shù)據(jù)統(tǒng)計分析方法回顧*

姜 博王麗敏劉 艷△李鎰沖△

復(fù)雜抽樣數(shù)據(jù)統(tǒng)計分析方法回顧*

姜 博1王麗敏2劉 艷1△李鎰沖2△

當今社會科學(xué)與健康科學(xué)調(diào)查研究，尤其是大規(guī)模調(diào)查，往往涉及多地區(qū)或多中心的抽樣問題，采取單純隨機抽樣選擇樣本因調(diào)查對象過于分散，成本高，可行性低［1］，調(diào)查設(shè)計者更傾向于可行性較高的復(fù)雜抽樣，但其通常使樣本結(jié)構(gòu)復(fù)雜化。若采用忽略抽樣特征的傳統(tǒng)統(tǒng)計學(xué)方法分析此類數(shù)據(jù)，會導(dǎo)致標準誤的低估，進而低估可信區(qū)間，且增大犯I類錯誤的可能性，最終導(dǎo)致偏倚甚至得到錯誤的統(tǒng)計推斷［2］。目前，對于復(fù)雜抽樣數(shù)據(jù)的統(tǒng)計分析主要分為基于設(shè)計和基于模型兩種方法體系［3］，本文對這兩種分析體系的主要文獻進行了回顧。

復(fù)雜抽樣簡介

復(fù)雜抽樣指在抽樣過程中采用除一階段單純隨機抽樣外，其他抽樣方法或其組合的抽樣方案。復(fù)雜抽樣通常具有分層、整群、不等概率或多階段等設(shè)計特點，其產(chǎn)生的樣本稱為復(fù)雜樣本。復(fù)雜抽樣優(yōu)勢在于：節(jié)省人力物力，使大規(guī)模調(diào)查更具可行性；可靈活調(diào)整樣本量在各級抽樣單位中的分配；可通過改變抽樣比來提高子總體的代表性和估計的可靠性。因此，目前在衛(wèi)生領(lǐng)域調(diào)查研究中，復(fù)雜抽樣設(shè)計已非常普遍［4］，許多大規(guī)模國家級調(diào)查均采用了復(fù)雜抽樣設(shè)計，如2010年中國慢性病及其危險因素監(jiān)測［5］、美國全國健康及營養(yǎng)狀況調(diào)查［6］等。

復(fù)雜樣本結(jié)構(gòu)

復(fù)雜抽樣設(shè)計往往使樣本具有明顯層次性，即樣本信息在一定地理區(qū)域或范圍內(nèi)存在聚集性［7］，其內(nèi)個體彼此不獨立。以2010年慢性病及其危險因素監(jiān)測多階段復(fù)雜抽樣設(shè)計為例：第一階段在所有162個監(jiān)測縣／區(qū)中按不等概率方法（與人口規(guī)模成比例的抽樣方法，PPS）隨機抽取4個鄉(xiāng)鎮(zhèn)；第二階段在每個抽中的鄉(xiāng)鎮(zhèn)中利用PPS法隨機抽出3個村；第三階段在每個抽中的村中利用整群抽樣隨機抽取居民戶；第四階段從抽中的居民戶中隨機抽取1名符合條件的居民作為調(diào)查對象［5］。四個階段抽樣將樣本分為5個水平，1水平是居民，2水平是居民戶，依次類推，每個水平包含多個抽樣單位即鄉(xiāng)鎮(zhèn)是縣／區(qū)的抽樣單位，依次類推。生活在同一水平、單位間的居民因有相同的經(jīng)濟、環(huán)境等因素，常具有相似的生活習(xí)慣，使得居民個體觀測指標數(shù)據(jù)有明顯層次聚集性，這種數(shù)據(jù)稱為層次結(jié)構(gòu)數(shù)據(jù)。這種現(xiàn)象廣泛存在于自然界和人類社會中，衛(wèi)生領(lǐng)域大規(guī)模調(diào)查更是無法避免接觸此類數(shù)據(jù)。因此，能夠解釋復(fù)雜樣本層次結(jié)構(gòu)的統(tǒng)計分析方法就顯得尤為重要。

復(fù)雜樣本分析方法

針對復(fù)雜樣本，目前有兩種統(tǒng)計分析方法體系，即基于設(shè)計和基于模型的統(tǒng)計分析方法，二者主要區(qū)別在于假設(shè)總體是否來自于一個無限的超總體［3］。前者不依賴于數(shù)據(jù)分布特征，通過對樣本的抽樣設(shè)計特點來分析并解釋數(shù)據(jù)；后者則不考慮設(shè)計因素，利用相應(yīng)模型假設(shè)進行分析［8］。

1．基于設(shè)計的統(tǒng)計分析方法

（1）描述性統(tǒng)計

基于設(shè)計的統(tǒng)計描述方法常結(jié)合權(quán)重進行構(gòu)造，權(quán)重包括三個方面：抽樣權(quán)重、無應(yīng)答權(quán)重和事后分層權(quán)重［9］，可表示為：

ws為抽樣權(quán)重，wr為無應(yīng)答權(quán)重，wps為事后分層權(quán)重。抽樣權(quán)重為入樣單元被抽中概率倒數(shù)，若存在多階段抽樣，則為各階段入樣單元權(quán)重之積［10］。無應(yīng)答權(quán)重為樣本應(yīng)答率倒數(shù)，可用與應(yīng)答率相關(guān)變量分層計算。事后分層權(quán)重目的在于將樣本特征調(diào)整與目標總體一致，其計算需將目標總體與樣本按關(guān)鍵指標分層，分別計算各層目標總體總量與累計權(quán)重（抽樣權(quán)重與無應(yīng)答權(quán)重）之和，最終形式即每層總體總量與累計權(quán)重之比［11］。利用權(quán)重，均數(shù)可表示為：

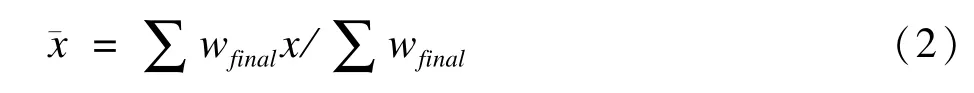
率可表示為：

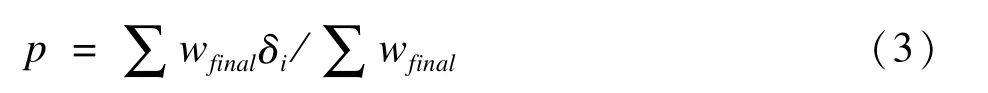
δi表示當?shù)趇個對象具有某特征，則δi＝1，否則δi＝0。

對于方差估計，主要包括泰勒級數(shù)線性近似法、刀切法、平衡半樣本法［12］。泰勒級數(shù)線性近似法基本思想是利用泰勒級數(shù)方法將非線性統(tǒng)計量線性化，然后計算方差的估計值［2，9］。刀切法基本思想是將總體分成k組，每次抽取時從中去掉一組，得到的多個二次抽樣樣本，每個二次樣本可得到一個均數(shù)或率的估計值，根據(jù)估計值的差異估計方差［13］。平衡半樣本法基本思想是假設(shè)總體分成L層，從每層隨機抽取兩個樣本單位，共抽取2L次，產(chǎn)生2L個半樣本，得到多個均數(shù)或率的估計值，利用多個估計值的差異估計方差［12，14］。研究顯示，泰勒級數(shù)線性近似法更為穩(wěn)定［15］，應(yīng)用范圍更廣［16］。為簡化計算，SAS等統(tǒng)計軟件應(yīng)用泰勒級數(shù)線性近似法估計方差時一般只考慮初級抽樣單元的數(shù)目，而忽略其他級別抽樣單元［17］，當初級抽樣單元抽樣比例較小時，方差估計的偏倚也較小［18］。

基于設(shè)計的統(tǒng)計推斷方法適合大樣本層次結(jié)構(gòu)數(shù)據(jù)，估計較為精確、穩(wěn)定［8］，對于小樣本數(shù)據(jù)、缺失數(shù)據(jù)等情況可能造成估計偏倚［3］。

（2）分析性統(tǒng)計（關(guān)系或效應(yīng)估計）

基于設(shè)計的統(tǒng)計分析方法是將權(quán)重引入模型。若因變量為連續(xù)型變量，常用基于設(shè)計的線性回歸模型。其模型參數(shù)估計方法根據(jù)偽極大似然法推導(dǎo)出［19］：

w表示權(quán)重，Y＝（Y1…Yn）T，XT＝（x1…xn）。

若因變量為分類變量，常用基于設(shè)計的logistic回歸模型，其采用極大似然法估計參數(shù)，似然函數(shù)為［20－21］：

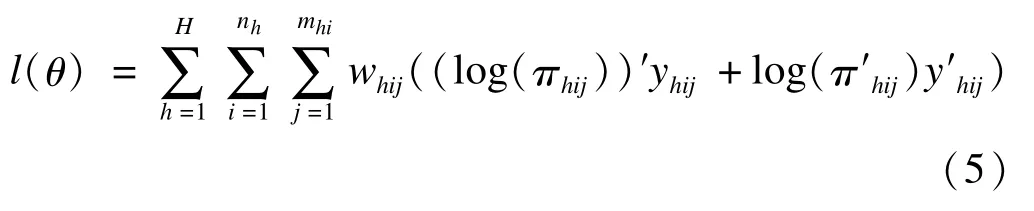
H為分層抽樣層數(shù)，h＝1，2，…，H；i為第h層中第i單位，i＝1，2，…，nh；j為第h層中第i單位的第j個觀測值，j＝1，2，…，mhi，h層中總計mhi個觀測值；whij為權(quán)重；y為結(jié)局變量。以二分類為例，yhij表示y第一類的指示變量，y′hij表示y第二類的指示變量；πhij是y的期望向量。

基于設(shè)計的方法不足在于，需要足夠樣本量，即使大型調(diào)查研究中，也可能出現(xiàn)某些地區(qū)樣本量較小導(dǎo)致結(jié)果不可靠；覆蓋不全、無應(yīng)答等情況導(dǎo)致抽樣隨機化假定被破壞，造成偏倚［16］。基于設(shè)計的統(tǒng)計分析方法應(yīng)用較為廣泛，如英國健康調(diào)查、英國社會態(tài)度調(diào)查等［22］。

2．基于模型的統(tǒng)計分析方法

（1）描述性統(tǒng)計

基于模型的方法通過擬合相應(yīng)模型進行統(tǒng)計描述。對于計量資料，假設(shè)數(shù)據(jù)滿足線性模型，Y＝β＋e且e～（0，δ），β的估計值即為樣本均數(shù)，可用公式＝計算，采用正態(tài)近似法估計總體均數(shù)雙側(cè)可信區(qū)間為同理對于計數(shù)資料，假設(shè)數(shù)據(jù)滿足二項分布概率模型，總體概率π的估計值p＝X／n，正態(tài)近似法估計總體概率雙側(cè)可信區(qū)間為p±uα／2Sp。

另一種描述方法是根據(jù)超總體模型理論，假設(shè)所研究的總體是隨機從超總體中抽取的一個樣本。對總體參數(shù)的統(tǒng)計推斷轉(zhuǎn)變?yōu)轭A(yù)測未抽中單元［23］，即在某種特定模型假設(shè)條件下，利用樣本數(shù)據(jù)估計未抽到數(shù)據(jù)，進而估計總體參數(shù)［24］。

如公式所示，從總體中抽取樣本S后，總體總和Y被分解為兩個部分。其中是抽取到的樣本集合屬于未抽中部分，通過樣本S擬合相應(yīng)模型進行估計。通過此方法可以估計總體總和、均數(shù)、比率、方差等，具體計算方法可參考相關(guān)文獻［3，23－24］，目前超總體模型在衛(wèi)生領(lǐng)域的應(yīng)用并不多見。

基于模型的統(tǒng)計推斷方法可適用于小樣本問題、數(shù)據(jù)缺失問題、離群值問題［3］，但其對模型的假設(shè)有較高要求，也無法很好描述層次結(jié)構(gòu)數(shù)據(jù)［23］。

（2）分析性統(tǒng)計

基于模型的方法采用適當?shù)哪Ｐ蛠頂M合數(shù)據(jù)，如線性模型、多水平模型等。多水平模型與傳統(tǒng)模型（線性模型、logistic回歸模型等）區(qū)別在于其將總的隨機誤差分解到相應(yīng)水平中，每個水平都有與其誤差項相應(yīng)的殘差、方差與協(xié)方差項，最終構(gòu)建適應(yīng)層次結(jié)構(gòu)數(shù)據(jù)具有復(fù)雜誤差結(jié)構(gòu)的模型［25］。多水平模型中因變量可為定量或定性變量，以多水平logistic回歸模型為例，擬合兩水平隨機效應(yīng)模型［7］。

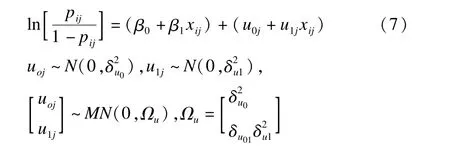
i為1水平；j為2水平；β0為平均截距，u0j為截距的隨機變量；β1為平均斜率，u1j為平均斜率的隨機變量；（β0＋β1xij）為固定效應(yīng)，（u0j＋u1jxij）為隨機效應(yīng)，以迭代廣義最小二乘法與邊際擬似然法等方法估計參數(shù)。

因?qū)哟谓Y(jié)構(gòu)數(shù)據(jù)有聚集性特點，應(yīng)用傳統(tǒng)模型將導(dǎo)致各參數(shù)及方差估計不準確，并可能掩蓋不同水平對反應(yīng)變量的影響，導(dǎo)致錯誤結(jié)論［25］，而多水平模型可以有效將各水平作用分離出來，較精確地調(diào)整因不同水平個體間相關(guān)性對結(jié)果產(chǎn)生的偏倚［26］；可有效處理缺失值問題［27］。其不足在于，各水平單位數(shù)量不能太少；模型參數(shù)估計與假設(shè)檢驗較復(fù)雜［28］。多水平模型常用于注重區(qū)域影響作用的調(diào)查，如不同水平醫(yī)學(xué)心理學(xué)調(diào)查研究［29］、不同地區(qū)兒童生長發(fā)育影響因素調(diào)查研究［30］等。

3．基于設(shè)計的模型輔助方法

若樣本來自于不等概率的抽樣設(shè)計，忽略設(shè)計特點可能導(dǎo)致估計的偏倚［31］。基于設(shè)計的分析方法雖考慮了權(quán)重的影響，但對數(shù)據(jù)的處理僅停留在一水平單位［32］，無法同時考慮各水平的影響，且對缺失數(shù)據(jù)較敏感。所以能夠同時汲取二者優(yōu)點，相互取長補短的方法具有較強的理論吸引力和應(yīng)用價值。近20年來，許多統(tǒng)計學(xué)家積極探索基于設(shè)計的模型輔助方法，加權(quán)多水平模型（weighted multilevelmodels）即為其中重要的一部分。

加權(quán)多水平模型從抽樣理論與多水平模型理論兩個角度綜合對層次結(jié)構(gòu)數(shù)據(jù)進行分析，利用權(quán)重減小不等概率抽樣在參數(shù)估計中產(chǎn)生的偏倚，又能同時分析多個水平單位的影響。加權(quán)多水平模型的模型結(jié)構(gòu)與一般多水平模型相似，但加權(quán)多水平模型是利用偽極大似然估計法進行參數(shù)估計［33－34］：

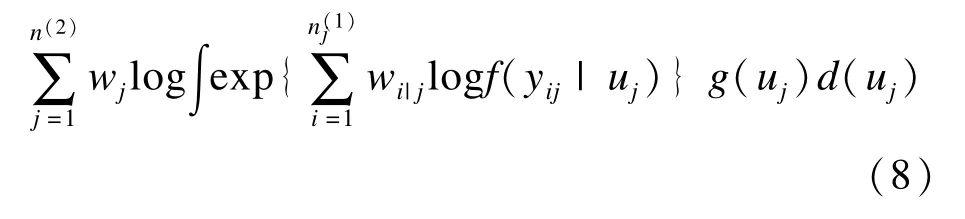
i為1水平，j為2水平，權(quán)重wj＝1／πj，wi｜j＝1／πi｜j，標準誤可根據(jù)泰勒線性三明治法計算。模型中，需分別計算各水平權(quán)重，但如果樣本量較少會導(dǎo)致偽極大似然估計產(chǎn)生偏倚，為減小偏倚可以調(diào)整權(quán)重。以兩水平為例，目前權(quán)重縮放（scaling of weights）常用計算方法有兩種，其一是Pfeffermann等于1998年提出，另一種是由Longford等于1995年提出［35］：

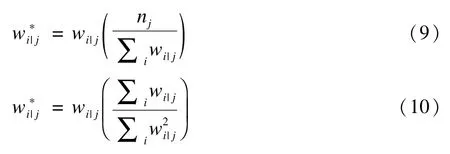
加權(quán)多水平模型可通過SAS 9．4版本GLIMMIX過程、Stata軟件gllamm分析模塊實現(xiàn)。目前由于權(quán)重的收集與計算較復(fù)雜、統(tǒng)計學(xué)軟件支持較少等原因，加權(quán)多水平模型的應(yīng)用較少，還處于推廣之中。

結(jié) 論

目前公共衛(wèi)生領(lǐng)域大規(guī)模調(diào)查研究中，復(fù)雜抽樣的應(yīng)用十分廣泛，基于設(shè)計和基于模型的統(tǒng)計分析方法都可以普遍應(yīng)用在復(fù)雜樣本，有研究表明，在大樣本的條件下，其估計結(jié)果相差不大［21］，可根據(jù)調(diào)查研究目的、抽樣設(shè)計等因素選擇相應(yīng)的方法，在抽樣框信息完整，樣本量足夠大的前提下，推薦使用基于設(shè)計的統(tǒng)計分析方法；抽樣信息不完整時或更多考慮層次結(jié)構(gòu)關(guān)系的前提下，推薦使用基于模型的統(tǒng)計分析方法。而加權(quán)多水平模型綜合了兩種方法優(yōu)點即在統(tǒng)計分析時，不僅考慮抽樣設(shè)計而且考慮層次結(jié)構(gòu)關(guān)系，具有較大的使用價值和推廣意義，可以為衛(wèi)生及相關(guān)領(lǐng)域政策的制定提供更加全面、精確的參考。

［1］Warszawski J，Messiah A，Lellouch J，et al．Estimating means and percentages in a complex sampling survey：application to a French national survey on sexual behaviour（ACSF）．Stat Med，1997，16（4）：397-423．

［2］劉建華，金水高．復(fù)雜抽樣調(diào)查總體特征量及其方差的估計．中國衛(wèi)生統(tǒng)計，2008，25（4）：377-379．

［3］金勇進，賀本嵐．復(fù)雜抽樣推斷方法體系的比較研究．統(tǒng)計與信息論壇，2011，26（10）：3-8．

［4］Osborne JW．Best Practices in using large，complex samples：The importance of using appropriate weights and design effect compensation．Practical Assessment，Research＆Evaluation，2011，16（12）：1-7．

［5］趙文華，寧光．2010年中國慢性病監(jiān)測項目的內(nèi)容與方法．中華預(yù)防醫(yī)學(xué)雜志，2012，46（5）：477-479．

［6］ES Ford WHG，Dietz WH．Prevalence of themetabolic syndrome among US adults：findings from the third National Health and Nutrition Exam ination Survey．Jama，2002，287（3）：356-359．

［7］楊珉，李曉松主編．醫(yī)學(xué)和公共衛(wèi)生研究常用多水平統(tǒng)計模型．北京：北京大學(xué)醫(yī)學(xué)出版社，2007：374-374．

［8］DCWheeler JEV，Paskett E．A Comparison of Design-based and Model-based Analysis of Sample Surveys in Geography．The Professional Geographer，2008，60（4）：466-477．

［9］West BT．Statistical and methodological issues in the analysis of complex sample survey data：practical guidance for trauma researchers．JTrauma Stress，2008，21（5）：440－7．

［10］胡楠，姜勇，李鎰沖，等．2010年中國慢病監(jiān)測數(shù)據(jù)加權(quán)方法．中國衛(wèi)生統(tǒng)計，2012，29（3）：424-426．

［11］Little R．Post-stratification：a modeler′s perspective．J Am Stat Assoc，1993，88（423）：1001-1012．

［12］王曉榮，趙俊康，王彤．復(fù)雜抽樣下的截取回歸模型在醫(yī)學(xué)研究中的應(yīng)用．中國衛(wèi)生統(tǒng)計，2012（5）：691-697．

［13］D Krewski JR．Inference from stratified samples：properties of the linearization，jackknife and balanced repeated replication methods．The Annals of Statistics，1981，9（5）：1010-1019．

［14］呂萍．重權(quán)數(shù)在復(fù)雜調(diào)查的方差估計中的應(yīng)用．統(tǒng)計研究，2011（2）：93-99．

［15］Paben SP．Comparison of Variance Estimation Methods for the National Compensation Survey：Proceedings of the Section on Survey Research Methods，American Statistical Association，1999．［16］Statistics-stockholm gk-jofo．Models in the practice of survey sampling（revisited）．JOURNAL OF OFFICIAL STATISTICS-STOCKHOLM，2002，18（2）：129-154．

［17］SAS Institute Inc．2011．SAS／STAT？9．3 User′s Guide．Cary，NC：SAS Institute Inc．

［18］Rao J．Interplay between sample survey theory and practice：an appraisal．Survey Methodology，2005，31（2）：117-138．

［19］Li J．Regression Diagnostics for Complex Survey Data：Identification of Influential Observations．Ann Arbor：Proquest，2007：5-8．

［20］繆凡，童峰．復(fù)雜抽樣數(shù)據(jù)的logistic回歸分析方法及其應(yīng)用．中國衛(wèi)生統(tǒng)計，2008，25（6）：577-579．

［21］陳丹萍．廣義線性混合效應(yīng)模型（GLMM）與復(fù)雜抽樣的logistic回歸模型在分層整群抽樣數(shù)據(jù)分析中的比較：復(fù)旦大學(xué)，2010．

［22］Rafferty A．Introduction to Complex Sample Design in UK Government Surveys．London：ESDSGovernment，2011：21-33．

［23］鄒國華，馮士雍．超總體模型下有限總體的估計．系統(tǒng)科學(xué)與數(shù)學(xué)，2007，27（1）：27-38．

［24］艾小青，金勇進．有限總體的估計——基于超總體模型．統(tǒng)計教育，2009，（2）：3-6．

［25］孫振球主編．醫(yī)學(xué)統(tǒng)計學(xué)（第3版）．北京：人民衛(wèi)生出版社，2002：445-464．

［26］C Duncan KJ，Moon G．Context，composition and heterogeneity：usingmultilevelmodels in health research．SocSciMed，1998，46（1）：97-117．

［27］王艷梅，王潔貞，丁守鑾，等．多水平模型在縱向研究資料中的應(yīng)用．山東大學(xué)學(xué)報（醫(yī)學(xué)版），2007，（7）：658-661．

［28］谷曉然．資本資產(chǎn)定價之收益率影響因素分析——基于多水平模型的實證研究：云南財經(jīng)大學(xué)，2012．

［29］張巖波，張海敏，何大衛(wèi)．多水平模型及其在醫(yī)學(xué)心理領(lǐng)域中的應(yīng)用．山西醫(yī)科大學(xué)學(xué)報，2001，（6）：510-512．

［30］金芳，倪宗瓚，李曉松，等．多元多水平模型及其在兒童生長發(fā)育研究中的應(yīng)用．中國衛(wèi)生統(tǒng)計，2004，（04）：13-15．

［31］D Pfeffermann CJS，Holmes DJ．Weighting for unequal selection probabilities in multilevelmodels，1998，60（1）：23-40．

［32］Asparouhov T．Weighting for unequal probability of selection in multilevelmodeling．Mplusweb notes，2004（8）：1-28．

［33］SRabe-Hesketh．Multilevelmodelling of complex survey data．J．R．Statist．Soc．A，2006，169：805-827．

［34］于石成，廖加強，等．復(fù)雜抽樣數(shù)據(jù)多水平模型分析方法及其應(yīng)用．中國衛(wèi)生統(tǒng)計，2014，31（2）：1-5．

［35］Carle AC．Fittingmultilevelmodels in complex survey data with design weights：Recommendations．BMCMedical Research Methodology，2009，9（1）：49．

（責任編輯：劉 壯）

國家自然科學(xué)基金（81202287）

1．哈爾濱醫(yī)科大學(xué)衛(wèi)生統(tǒng)計教研室（150081）

2．中國疾病預(yù)防控制中心慢性非傳染性疾病預(yù)防控制中心

△通信作者：李鎰沖，E-mail：alexleeliyichong＠gmail．com；劉艷，E-mail：liuyan＠ems．hrbmu．edu．cn