塊Toeplitz矩陣低復雜度求逆的衛(wèi)星導航空時抗干擾算法*

吳舜曉，黃仰博，聶俊偉，歐 鋼

(國防科技大學電子科學與工程學院，湖南長沙410073)

衛(wèi)星導航信號到達地面時非常微弱，極易受到有意或無意干擾，軍用接收機系統(tǒng)和航空應用系統(tǒng)通常采用自適應天線陣技術來提高其抗干擾能力［1］。為同時利用空域與時域自由度，抗干擾天線陣通常采用空時自適應處理［2］(Space-Time Adaptive Processing，STAP)算法。對于接收衛(wèi)星導航信號的天線陣列，由于導航信號用于測距，傳統(tǒng)的窄帶假設不再適應現(xiàn)實要求，需采用可描述整個通道內(nèi)各頻率點處陣列響應的寬帶模型［3-4］。針對陣列的寬帶模型，需要通過增加時序抽頭個數(shù)來提高STAP處理的自由度，由此可以更好地補償各陣元接收信號群時延差異，達到更好地抑制干擾和增強有用信號的效果［5-6］。設陣元個數(shù)為N，每個陣元后的抽頭個數(shù)為K，則對于功率倒置、最大信干噪比等常用空時自適應處理準則，直接全精度求解自適應權值向量需要對(N·K)×(N·K)維的采樣協(xié)方差矩陣求逆，其計算復雜度為O［(N·K)3］。可見增加時域抽頭個數(shù)，將使得STAP處理的計算量及相應的工程實現(xiàn)代價急劇增大，限制了其在機載、彈載等小型化武器平臺上的廣泛應用。

針對STAP中矩陣求逆計算量大的問題，早期的文獻從準最優(yōu)的角度提出了以多級維納濾波為代表的降秩、降維方法［7］。近年來，隨著數(shù)字信號處理實現(xiàn)技術的發(fā)展，直接快速實現(xiàn)矩陣求逆運算變?yōu)榭赡埽琑osado等在2012年提出了直接在可編程門陣列(Field Programmable Gate Array，F(xiàn)PGA)中實現(xiàn)矩陣求逆的方法［8］。為達到更好的抗干擾性能，適應更嚴苛的應用環(huán)境，采用直接對采樣協(xié)方差矩陣求逆方法(Sample Matrix Inversion，SMI)的STAP正逐漸取代準最優(yōu)方法，任磊等對用數(shù)字信號處理器(Digital Signal Processor，DSP)實現(xiàn)SMI進行了深入的研究［9］。為進一步減少實現(xiàn)代價，大量文獻針對減少矩陣求逆的計算量和實現(xiàn)結(jié)構(gòu)展開了研究。Zhu等針對無線通信應用環(huán)境下協(xié)方差矩陣的特點提出了加速矩陣求逆的算法［10］。針對雷達信號處理中的采樣協(xié)方差矩陣具有Hermite對稱性的特點，高飛、Yang等提出了矩陣求逆的并行實現(xiàn)結(jié)構(gòu)和快速求逆算法［11-12］。然而，上述傳統(tǒng)矩陣求逆方法的計算量仍然與K3成正比，其計算量仍然會隨著抽頭個數(shù)的增加而快速增長。針對此問題，本文通過提出新的協(xié)方差矩陣近似估計方法，以使得采樣協(xié)方差矩陣具有便于實現(xiàn)求逆運算的結(jié)構(gòu)特點。根據(jù)在平穩(wěn)條件下協(xié)方差矩陣可表示為塊Toeplitz矩陣的特性，新的協(xié)方差矩陣估計方法可保證所得到的采樣協(xié)方差矩陣同時為塊Toeplitz矩陣與Hermite矩陣，且對于通常的導航應用來說，此種近似對抗干擾性能的影響很小。在此基礎上通過運用塊Toeplitz矩陣低復雜度求逆算法，使得矩陣求逆問題的計算量與K2成正比。

1 協(xié)方差矩陣特性分析

1.1 空時濾波器實現(xiàn)結(jié)構(gòu)

圖1所示為N個陣元，每個陣元后有K個時延抽頭的GNSS抗干擾空時濾波器實現(xiàn)結(jié)構(gòu)。在空間傳播的射頻信號經(jīng)過各個天線陣子接收、射頻前端等處理后得到復基帶信號。各路復基帶信號再被依次延時到各抽頭上，各抽頭上的信號與相應的權值相乘后再通過求和得到陣列的輸出y。設射頻前端的帶寬為B，空時濾波器處理的數(shù)據(jù)率為，則要求抽頭時間間隔T略小于設陣元的編號為1，2，…，N，抽頭按照先后順序編號為1，2，…，K，陣元m后第u個抽頭處的采樣值序列為xmu［k］，與之對應的加權系數(shù)求共軛以后為wmu。

用向量X表示各抽頭上的數(shù)據(jù)，向量W表示與各抽頭對應的加權系數(shù)，則整個陣列的輸出可表示為:

式中，上標H表示對矩陣進行共軛轉(zhuǎn)置操作，下文中都采用此符號。將陣列信號看成多維隨機變量，則其協(xié)方差矩陣為:

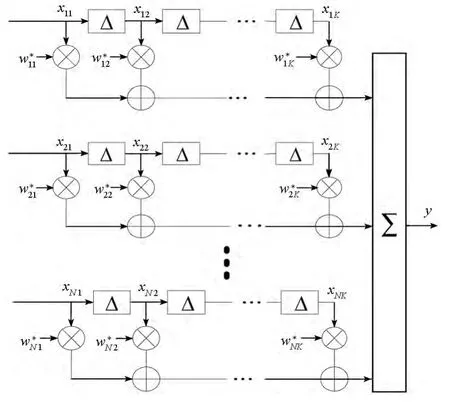
圖1 空時濾波結(jié)構(gòu)Fig.1 Space-time filtering structure

空時權值求解中通常需要求解如式(3)所示的線性方程組［11］:

其中b為由抗干擾準則所決定的約束向量。式(3)的解為，因此通過求協(xié)方差矩陣的逆來求解式(3)是SMI方法的關鍵步驟。本文采用按照先陣元編號，后抽頭先后順序排列向量X中各變量，即

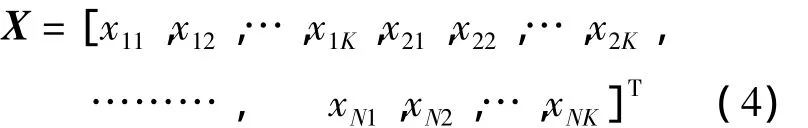
相應地，W中各變量的排列順序如下:

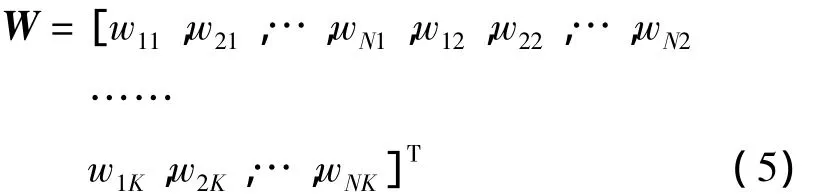
1.2 平穩(wěn)條件下的協(xié)方差矩陣特性

為了便于發(fā)現(xiàn)協(xié)方差矩陣的特征，先在一種較理想的條件下進行分析。為此，假設各陣元上的信號滿足平穩(wěn)性條件，即各陣元上的信號是平穩(wěn)的且各陣元信號之間也是聯(lián)合平穩(wěn)的。在平穩(wěn)性條件成立的前提下，任意兩個抽頭處數(shù)據(jù)的互相關值，僅取決于信號到達這兩個抽頭的時延差。易知任意抽頭處的信號相對于參考陣元上參考抽頭信號的時延均由兩部分構(gòu)成，一部分由陣元空間位置確定，另一部由信號所經(jīng)過的抽頭個數(shù)決定，由此第m個陣元后的第u個抽頭處的時延為:

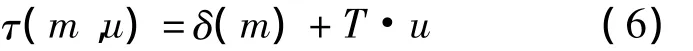
式(6)中函數(shù)δ(·)表示由陣元位置決定的時延。由此可知對于任意兩個抽頭處的信號xmu與xnv，其時延差為δ(m)-δ(n)+T(u-v)，即時延差的值僅取決于m，n與u-v。因此協(xié)方差矩陣中的構(gòu)成元素E(xmu xnv)的取值僅由m，n與u-v決定。設第u個抽頭處各陣元信號構(gòu)成的向量為X u，第v個抽頭處各陣元信號構(gòu)成的相位為X v，即:

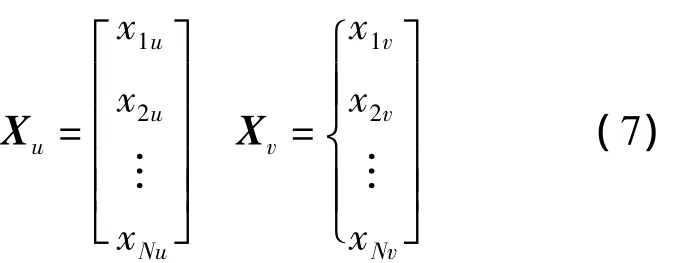
易知X u與X v的互相關矩陣僅與u-v有關，不妨設i=v-u，由此可表示為:

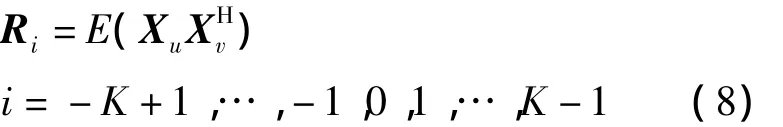
易知，X u與X v均為X中的子塊，由此可知R i是R xx中的N×N子塊，且其排列如式(9)所示:

1.3 采樣協(xié)方差矩陣計算

在實際的工程應用中需要利用采樣值近似計算得到的協(xié)方差矩陣估計值，即采樣協(xié)方差矩陣。雖然平穩(wěn)性假設不會嚴格成立，但在一次權值更新周期這樣短的時間內(nèi)，此假設可近似認為成立，因此可參照式(8)和式(9)的形式來估計協(xié)方差矩陣。此時只需要將式(8)中R i的數(shù)學期望運算用求平均值的運算來替代即可。設在一個權值更新周期中用L個采樣值參與估算協(xié)方差矩陣，則R i的第m行n列元素可按照式(10)近似計算

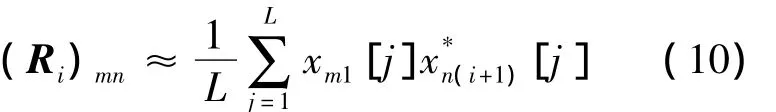
本文算法中的采樣協(xié)方差矩陣的計算方式為:先用式(10)得到R i的估計值，再將其帶入式(9)中得到采樣協(xié)方差矩陣。下文中，為書寫方便，采樣協(xié)方差矩陣及其構(gòu)成子塊仍然用R xx與R i表示。容易驗證本文算法所提的采樣協(xié)方差矩陣即是塊Toeplitz矩陣又是Hermite矩陣。

易知，與傳統(tǒng)的采樣協(xié)方差矩陣計算方法相比，本文的計算方法為保證所得結(jié)果的塊Toeplitz結(jié)構(gòu)，對參與求平均運算采樣點所對應的時間區(qū)間進行了平移，且平移范圍不超過K個采樣點。因此，只要K?L的條件成立，不管平穩(wěn)性假設是否成立，都能保證本文算法得到的采樣協(xié)方差矩陣與傳統(tǒng)方法得到的采樣協(xié)方差矩陣高度近似，因而性能差異小。通常情況下，為獲得高抗干擾性能，采樣協(xié)方差矩陣的計算由硬件電路完成，在一個權值更新周期內(nèi)的全部數(shù)據(jù)都被用于計算采樣協(xié)方差矩陣。例如:假設數(shù)據(jù)采樣率為20MHz，權值更新周期為1ms，則L的取值為20 000，然而一般情況下受實現(xiàn)資源的制約，通常有K〈20成立。因此，對于導航抗干擾應用來說K?L很容易滿足，大多數(shù)情況下都可采用塊Toeplitz結(jié)構(gòu)的采樣協(xié)方差矩陣來求解空時權值。

2 自適應權值求解

在得到了具有塊Toeplitz和Hermite結(jié)構(gòu)特性的采樣協(xié)方差矩陣以后，本節(jié)首先利用塊Toeplitz矩陣的快速求逆算法［13］得到求逆過程的迭代表示，然后結(jié)合其Hermite特性實現(xiàn)進一步優(yōu)化。

2.1 塊Toep litz矩陣的方程組迭代求解

本節(jié)將文獻［13］中的算法應用到求解式(3)以得到自適應權值，這里僅列出主要結(jié)果。將權值向量和約束向量寫成分塊形式，即

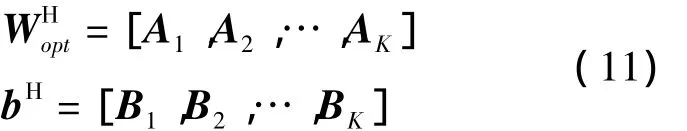
式中:A i為1×N的行向量，對應于各陣元在抽頭i處的加權系數(shù);B i也為1×N的行向量。由此可將最優(yōu)權值的求解問題表示為:

設L p+1，p=1，2，…，K-1的第一行子塊為R0，R-1至R-p且第一列子塊為R0，R1至R p的塊Toeplitz矩陣，即

為方便表述，對于構(gòu)成元素均為N×N矩陣的任意分塊矩陣C，引入兩個算符:一個為，表示對矩陣中的子塊進行轉(zhuǎn)置操作，即中第(i，j)子塊，正好是C中的第(j，i)子塊;另一個為，表示交換矩陣中同一行中各子塊的先后順序，即若設

利用上述符號，L p+1可表示為如下的迭代表達式:

式(14)中:

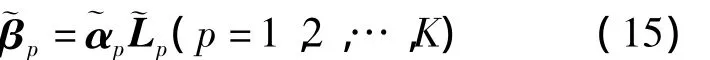
顯然，當取p=K時，所得方程即為式(12)的方程。為便于表述算法迭代過程，先定義如下變量和算符。

設I與Z分別為C N×N中的單位矩陣與零矩陣。在第p步迭代中，將式(15)的解拆分為p個C1×N中的向量，即

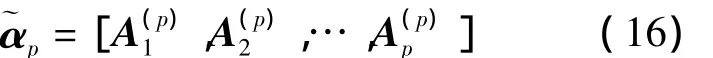
對于t=1，2，…，K-1定義迭代初始化及后續(xù)各步驟中的中間變量，包括:

1)N×N的矩陣Q(t)與S(t)，其逆矩陣分別表示為Q-1(t)與S-1(t);

2)由t個N×N的子矩陣塊排成一行得到的矩陣I s(t)與F q(t)。對于此兩個矩陣序列，定義算符(·)n表示取其中的第n個子塊，例如:(I s(t))1表示取I s(t)中的第1個子塊，(F q(t))t-1表示取F q(t)中的第t-1個子塊。

利用塊Toeplitz矩陣快速求逆算法的空時權值迭代求解流程如圖2所示。初始化階段由求解取p=1與p=2時式(15)的方程構(gòu)成，后續(xù)的K-2個迭代步驟對應于求解p=3，4，…，K時式(15)的方程。

在上述流程的初始化步驟中，先求解p=1時的方程，具體計算過程為:

再求解p=2時的方程，此時可部分地利用上一個步驟所得結(jié)果和中間變量，具體計算過程如下。

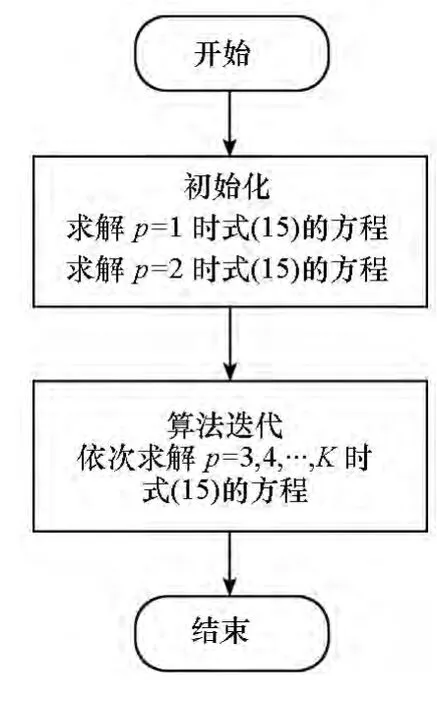
圖2 塊Toeplitz矩陣快速求逆的空時權值求解流程Fig.2 Solve the space-time weights by fast algorithm for block Toeplitz matrix inversion

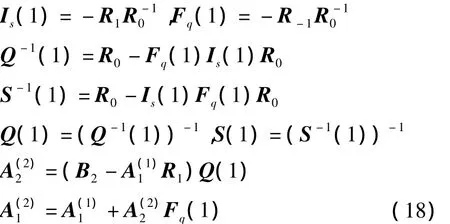
在迭代處理的方程求解中，不是直接對矩陣進行求逆，而是利用中間變量的遞推關系先計算出中間變量，再根據(jù)中間變量計算出方程的解。設迭代變量為h=1，2，…，K-1，則每一次迭代包括以下三步計算過程。

1)按照式(19)計算中間變量

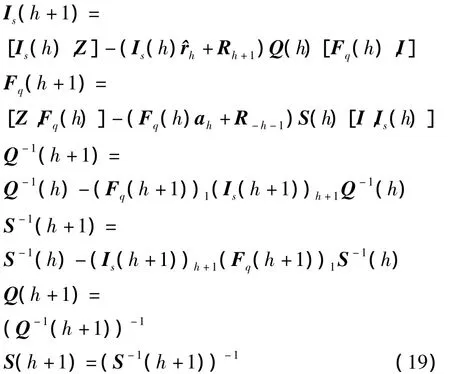
2)計算解向量中的最后一個1×N子塊，計算公式如下。

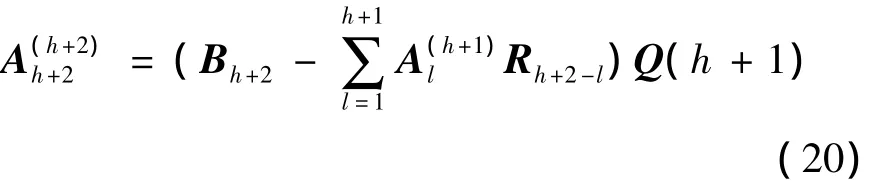
3)計算解向量的前h+1個1×N子塊，即對于l=1，2，…，h+1執(zhí)行以下計算

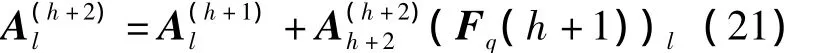
2.2 利用共軛對稱性的優(yōu)化

上一節(jié)迭代求解空時權值的算法僅利用了協(xié)方差矩陣為分塊Toeplitz矩陣的特點，沒有利用其Hermite對稱性。利用的對稱性，參照文獻［13］中的推導方法可知與互為共軛轉(zhuǎn)置;Q(p)，S(p)，)均為Hermite矩陣。根據(jù)上述特點，本文算法可進一步采用如下簡化處理:

2)計算Q-1(p)，S-1(p)時可只計算其下三角部分，上三角部分利用Hermite矩陣的對稱性得到;

3)對Q-1(p)，S-1(p)進行求逆計算Q(p)，S(p)時，可利用Hermite矩陣的對稱性減少計算量［11-12］。

從本文算法的迭代過程可知，Q(p)，S(p)均為N×N的矩陣;I s(p)，F(xiàn) q(p)均由p個N×N的子塊按行排列構(gòu)成為1×N的行向量。因此，算法的計算過程可分為以下5類基本運算:a)N×N矩陣的乘法;b)N×N矩陣的加減法;c)N×N矩陣的求逆;d)1×N向量與矩陣乘法;e)1×N向量之間的加減法。考慮到陣元數(shù)目N一般較小，且目前的FPGA已能較好地支持浮點運算，上述五類運算都可以在FPGA中快速實現(xiàn)并行處理，因此可以方便地利用FPGA來加速算法1的實現(xiàn)。

3 性能分析

本文算法用于簡化空時抗干擾處理中計算采樣協(xié)方差矩陣和對其進行求逆運算這兩個基本處理環(huán)節(jié)的計算量，因此可具體應用于多種抗干擾準則中。本文算法的目的是在保持與傳統(tǒng)算法性能接近的前提下大幅減少計算量。因此下面將通過數(shù)值仿真來比較本文算法與傳統(tǒng)算法在抗干擾性能上的差異，然后再分析本文算法的計算量。

3.1 抗干擾性能比較

為便于對比和簡化仿真，傳統(tǒng)算法和本文算法都采用工程實踐中最常用的功率倒置準則，即b為僅有一個為1，其余全部為0的向量，1對應參考陣元上的參考抽頭。針對導航信號的特點，干擾抑制性能采用等效陣列增益［3］來衡量。等效陣列增益描述的是陣列處理對解擴后獲得的載噪比所產(chǎn)生的影響，取正數(shù)表示增強了載噪比，取負數(shù)表示對載噪比造成了損耗。

仿真時有用信號用GPS的L2頻點P碼(調(diào)制碼率為10.23MHz的長碼)信號模擬，采用4元方陣，陣元間距為半波長，假設信號和干擾都為遠場入射。表1所示為設置的仿真條件和按照傳統(tǒng)方法計算采樣協(xié)方差矩陣與按照本文算法計算采樣協(xié)方差矩陣所分別得到的等效陣列增益。

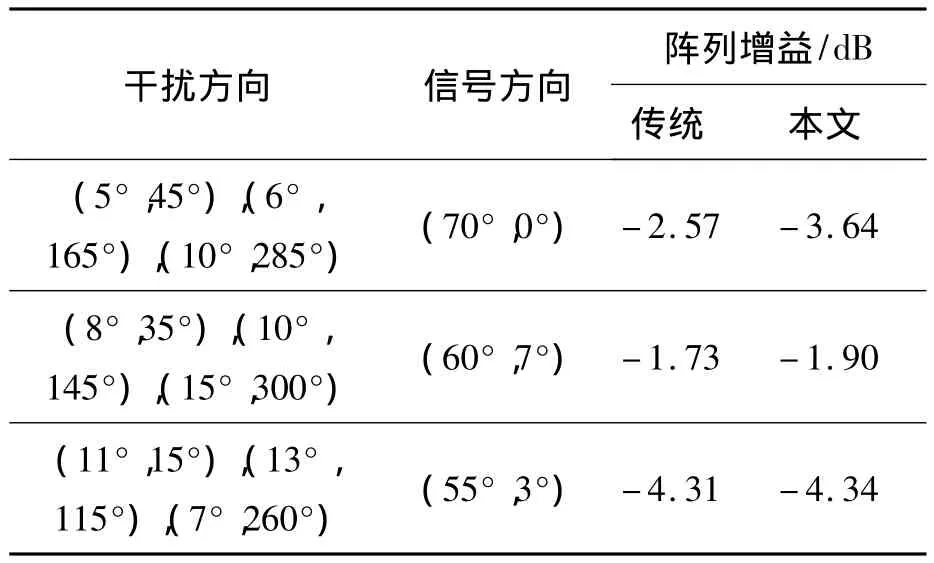
表1 仿真條件設置與陣列增益Tab.1 Simulation condition setting and array gain

表1的來波方向表示中，第一個數(shù)為俯仰角，第二個數(shù)為方位角。有三個由二相相移鍵控(Binary Phase Shift Keying，BPSK)調(diào)制產(chǎn)生的寬帶干擾和一個有用信號入射，干信比均為65dBc，K=9，L=21 000，單個陣元上的載噪比為43dBHz，數(shù)據(jù)采樣率(62/3)MHz，仿真時間長度為1.5s。取一組典型情況下本文算法所獲得的空時濾波權值，據(jù)此可計算出在整個信號通帶范圍內(nèi)各頻率處的陣列響應幅度如圖3所示。

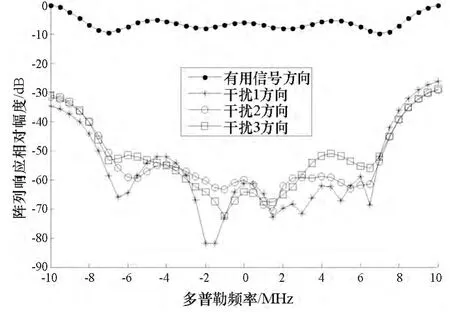
圖3 有用信號及干擾信號方向的陣列響應Fig.3 Array response in the direction of useful signal and jamming signals

從圖3可定性地看出，對于4元天線陣，本文算法確實可以在各干擾方向形成寬帶零陷。表1的等效陣列增益結(jié)果表明，雖然傳統(tǒng)算法的性能較優(yōu)，但與本文算法的性能差異不超過1dB。因此本文算法對采樣協(xié)方差矩陣的簡化計算方法是合理的，為了大幅減少計算量可以承受此種性能損耗。

3.2 計算量分析

本文算法不僅簡化了采樣協(xié)方差矩陣的計算，更重要的是縮小了其求逆運算的復雜度。下面將分析本文算法中根據(jù)采樣協(xié)方差矩陣求解空時權值的計算量。根據(jù)本文所提算法的特點，首先分析在一次空時權值求解過程中，2.2節(jié)中的5類基本運算各自的執(zhí)行次數(shù)，然后再根據(jù)各類運算的計算量得到總的計算量。最終得到以復數(shù)乘除法和加減法次數(shù)作為度量的計算量總和。利用互為共軛轉(zhuǎn)置的特點僅計算其中一個，并忽略對矩陣進行共軛轉(zhuǎn)置、交換子塊位置等操作的計算量，可得到初始化階段、每一步迭代和完整的算法執(zhí)行過程中5類基本運算的次數(shù)如表2所示。

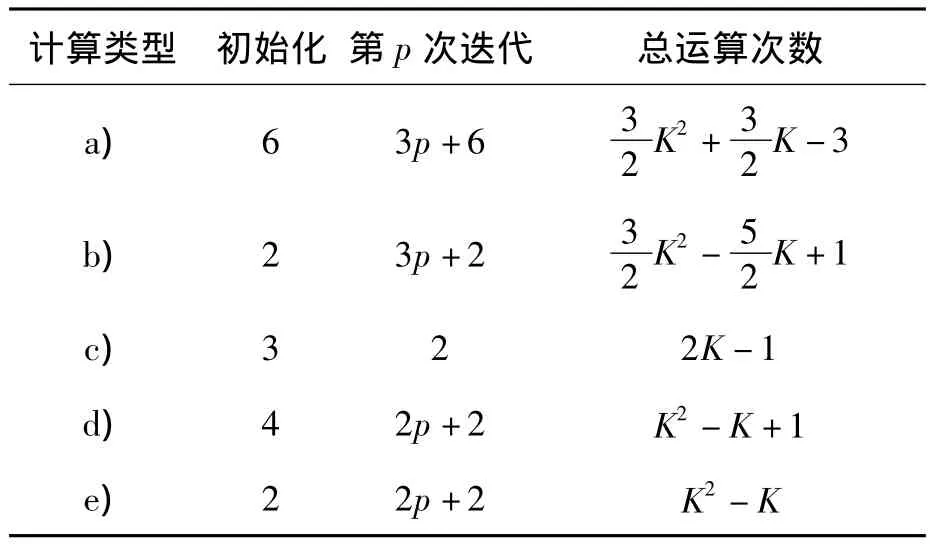
表2 算法1的計算量分析Tab.2 Analysis of computational load of algrithm 1

1)矩陣乘法的計算量為:

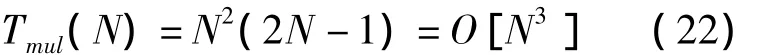
2)矩陣加減法的計算量可表示為:

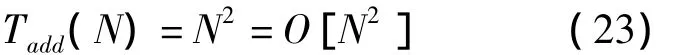
3)由于需要求逆的矩陣均為Hermite矩陣，故利用其對稱性可得到其計算量為［12］:

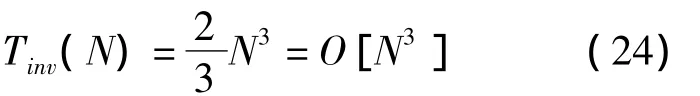
4)向量與矩陣乘法的計算量為:

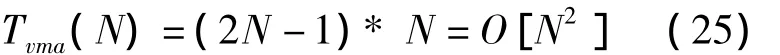
5)向量加減法的計算量為:

綜合以上分析可知，以復數(shù)乘除法和加減法次數(shù)衡量的算法總計算量為:

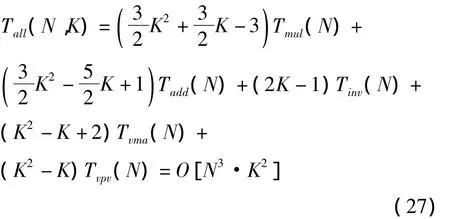
注意到通常的導航抗干擾天線陣中陣元個數(shù)N較小，故求解濾波權值的計算量主要取決于時域抽頭個數(shù)。式(27)表明，本文算法的計算量與K2成正比，因此隨著時域抽頭數(shù)K的增加，本文算法相比傳統(tǒng)算法減少的計算量越多。與現(xiàn)有的利用Hermite對稱性的矩陣求逆方法(計算量為對比，對于4陣元的典型情況，根據(jù)式(27)可計算得到，在抽頭數(shù)分別為9與15時，本章方法的計算量分別降低到現(xiàn)有方法計算量的65%與38%。

4 結(jié)論

在STAP處理中采用SMI方法時，計算量隨著時域抽頭個數(shù)的增加而急劇增加，工程實現(xiàn)代價較大。對此，本文提出了一種降低計算復雜度的空時抗干擾算法。該算法首先在平穩(wěn)性假設的啟發(fā)下，通過采用一種新的協(xié)方差矩陣近似計算方式，得到了具有塊Toeplitz矩陣結(jié)構(gòu)又具有Hermite對稱性的采樣協(xié)方差矩陣。然后，利用上述結(jié)構(gòu)特點，應用塊Toeplitz矩陣的線性方程快速求解算法，將空時權值求解的復雜度從傳統(tǒng)方法的O［N3·K3］降低到O［N3·K2］，很好地減少了權值求解的計算量。理論分析和數(shù)值仿真表明，新的協(xié)方差矩陣近似計算方法對抗干擾性能的影響較小，可以忽略不計。本文算法可大量用于各種涉及協(xié)方差矩陣求逆的空時處理中。

References)

［1］Fante R，Vaccaro J J.Wideband cancellation of interference in a GPS receive array［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36(2):549-564.

［2］王永良，彭應寧.空時自適應信號處理［M］.北京:清華大學出版社，2000.WANG Yongliang，PENG Yingning.Space time adaptive processing［M］.Beijing:Tsinghua University Press，2000.(in Chinese)

［3］聶俊偉，葛銳，李敏，等.窄帶假設對GNSS天線陣抗干擾性能評估的影響分析［J］.國防科技大學學報，2011，33(5):128-133.NIE Junwei，GE Rui，LI Min，et al.The Influence analysis of narrowband hypothesis to GNSS array anti-jamming performance evaluation［J］.Journal of National University of Defense Technology，2011，33(5):128-133.(in Chinese)

［4］O'Brien A J，Gupta I J.Comparison of output SINR and receiver C/N0 for GNSS adaptive antennas［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45(4):1630-1640.

［5］Moore T D，Gupta I J.The effect of interference power and bandwidth on space-time adaptive processing［C］//Proceedings of IEEE Antennas and Propagation Society International Symposium，2003.

［6］王瑛.衛(wèi)星導航天線陣抗干擾關鍵技術研究［D］.長沙:國防科學技術大學，2008.WANG Ying.Research on the key technologies of anti-jamming antenna arrays in satellite navigation systems［D］.Changsha:National University of Defense Technology，2008.(in Chinese)

［7］Goldstein J S，Reed I S，Scharf L L.Multistage representation of the wiener filter based on orthogonal projections［J］.IEEE Transactions on Information Theory，1998，44(7):2943-2959.

［8］Rosado A，Iakymchuk T，Bataller M，et al.Hardware-efficient matrix inversion algorithm for complex adaptive systems［C］//Proceedings of the 19th IEEE International Conference on Electronics，Circuits and Systems，2012.

［9］任磊，王永良，陳輝，等.基于DSP的SMI方法快速實現(xiàn)研究［J］.國防科技大學學報，2009，31(3):53-59.REN Lei，WANG Yongliang，CHEN Hui，et al.Research on fast implementation of SMI method based on DSP［J］.Journal of National University of Defense Technology，2009，31(3):53-59.(in Chinese)

［10］Zhu H F，Chen W，She F.Improved fast recursive algorithms for V-BLAST and G-STBC with novel efficient matrix inversion［C］//Proceedings of IEEE International Conference on Communications，2009.

［11］高飛，王永良，陳輝，等.STAP中的矩陣求逆問題研究［J］.雷達科學與技術，2008，6(3):215-218.GAO Fei，WANG YongLiang，CHEN Hui，et al.Study on matrix inversion for STAP［J］.Radar Science and Technology，2008，6(3):215-218.(in Chinese)

［12］Yang X P，Liu Y X，Long T.Pulse-order recursive method for inverse covariance matrix computation applied to spacetime adaptive processing［J］.Science China Information Sciences，2013，56(4):1-12.

［13］Akaike H.Block Toeplitz matrix inversion［J］.Siam Journal on Applied Mathematics，1973，24(2):234-241.