空間繩網系統展開動力學特性分析*

劉海濤，張青斌，楊樂平，朱彥偉

(國防科技大學航天科學與工程學院，湖南長沙410073)

近年來，一種繩網捕獲、繩系拖曳的離軌服務手段，在航天領域受到日益廣泛的關注［1-2］。如圖1所示，軌道拖船機動接近目標后，通過一定的發射方式，在空間展開一張由柔性細繩編織的繩網，形成特定構型覆蓋包裹目標，并利用連接到繩網上的系繩完成對目標的回收或離軌銷毀。作為一種柔性捕獲模式，繩網捕獲在非合作目標捕獲、遠距離捕獲等方面展現了極大的應用潛力。與傳統的機械臂捕獲方式相比，繩網捕獲具有壓縮體積小、發射質量輕、抓捕距離遠、容錯范圍大、對載體影響小等突出優勢［2］。

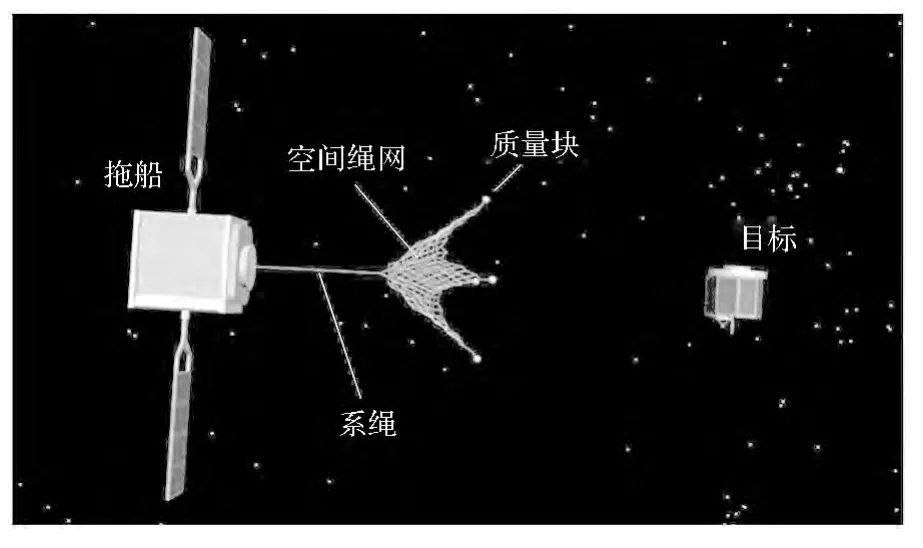
圖1 空間繩網捕獲示意圖Fig.1 Sketch map of space web capture

空間繩網極度柔軟，極易出現變形、松弛與纏繞［3］，具有非常復雜的非線性、多柔體動力學特性。由于目前仍然無法準確分析與預測空間繩網的動力學特性，太空與地面的繩網試驗過程中經常出現故障。例如，1999年俄羅斯Znamya 2.5反射鏡試驗出現失敗［4］，2006年日本Furoshiki試驗中出現了繩索纏繞與松弛現象［5］。國內外學者對空間繩網系統開展了大量研究工作。Mankala等［6］研究了繩系飛網系統的動力學建模與仿真問題，翟光等［7-8］研究了空間繩網系統的捕獲偏差與反饋控制問題，他們的研究中都將空間繩網視為質點。陳欽等［9-11］對空間繩網捕獲系統進行了系統設計，利用集中質點法建立了空間繩網系統剛柔耦合動力學模型，研究了繩網發射展開過程的動力學問題。于洋等［12-14］分別利用軟件THUsolver和ABAQUS建立了飛網拋射展開的有限元模型，研究了飛網在靜態和動態環境下的力學特性，比較了兩種飛網折疊方式的展開效果。馬駿等［15］設計了一種自主機動空間繩網機器人系統，針對該系統采用集中質量法建立了動力學模型。張青斌等［16-17］通過繩網地面試驗，校核和改進了空間繩網動力學模型，分析了地面環境和空間環境下繩網展開過程的差異性。本文在此研究基礎上進一步開展空間繩網系統動力學分析等方面的研究工作。

1 空間繩網動力學模型

1.1 模型描述

本文研究采用發射質量塊的方式展開空間繩網。空間繩網發射機構剖面圖如圖2所示，柔性繩網壓縮封裝在網艙內，質量塊軸對稱式安裝并分別連接在繩網的頂點上。當發射機構點火啟動后，質量塊會以一定的發射速度υ和發射張角α被彈出，牽引繩網逐漸展開并向前飛行。

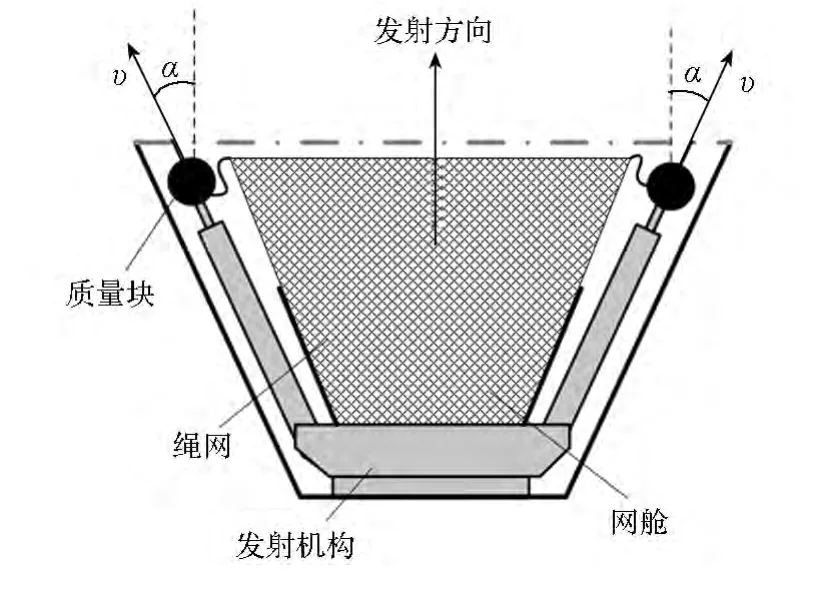
圖2 空間繩網發射機構剖面圖Fig.2 Section map of the trigger mechanism of space web

引入地心慣性系OE-XYZ和拖船軌道系O1-xyz，如圖3所示。其中拖船軌道系的x軸由地心OE指向拖船質心O1，z軸沿拖船軌道面法向，y軸在軌道面內垂直于x軸并指向運動方向。模型假設為:1)繩索可拉不可壓，有縱向的彈性和阻尼;2)忽略繩索結構中的彎曲撓性和接觸效應;3)地球視為均質球體，完全中心引力場;4)拖船運行于圓軌道，且不考慮空間繩網發射對拖船軌道的影響;5)不考慮空間繩網在網艙內的折疊位型及其在網艙所受的摩擦力。

空間繩網屬于典型的非線性、多柔體系統，目前還很難建立精確的解析模型。為此，采用離散化的建模思路，將空間繩網離散為若干有限段，然后將各繩段的質量集中在兩端點，即繩段節點。由于繩索極度柔軟，僅能承受拉力，故可假設繩段節點之間節點由“彈簧”相連，而且該“彈簧”只能承受張力，不能承受壓力，同時考慮到繩索的阻尼效應，可將各繩段處理為集中質量阻尼彈簧，這就是“半彈簧阻尼(semi-linear springs and dampers)”模型，如圖4所示。在后續的動力學建模中，首先計算各繩段的張力，然后計算各繩段所受的外力，并將其等效到繩段兩端的節點上，最后聯立各節點動力學方程，即可得到繩網系統的動力學方程。

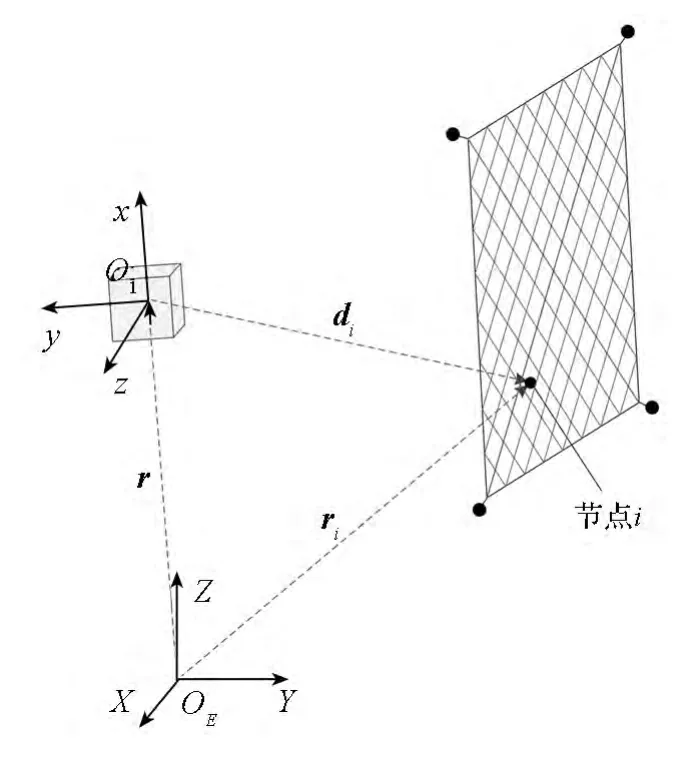
圖3 空間繩網的坐標系Fig.3 Coordinate frames of the space web

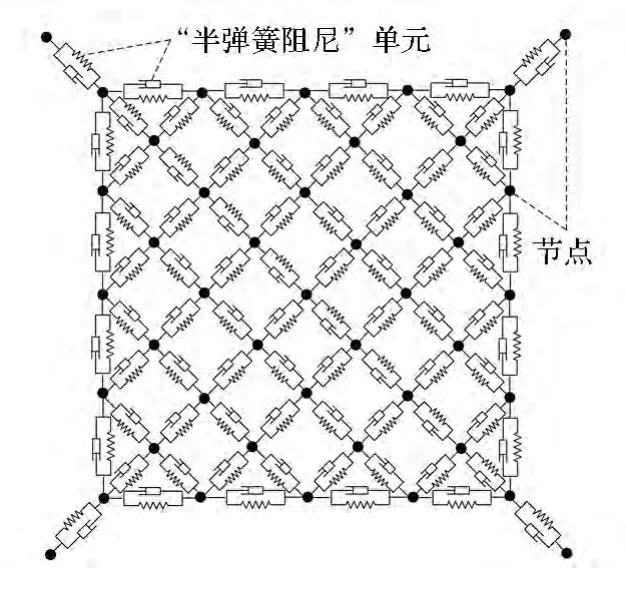
圖4 空間繩網的“半彈簧阻尼”模型Fig.4 Semi-linear springs and dampers model of the space web

1.2 繩段單元張力計算

由于繩索極度柔軟，僅能承受張力，不能承受壓力，同時考慮到繩索的阻尼效應，因此將各繩段單元假設為“半彈簧阻尼”單元。通常，繩段張力可近似為線彈性與線性阻尼之和，如圖5所示，繩段sij的張力大小為

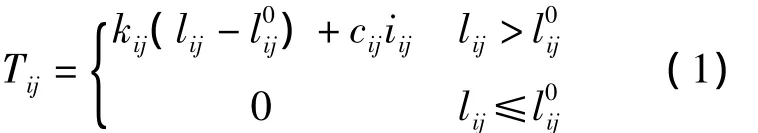
式中:lij，iij分別為繩段sij的實際長度及其變化率;kij，cij分別為繩段sij的等效彈性系數與等效阻尼系數，其取值一般通過試驗得出。

如圖5所示，繩段sij兩端的節點為節點i與節點j，在慣性系下的位置矢量分別為r i，r j，則繩段sij的實際長度lij及其變化率iij可如下計算

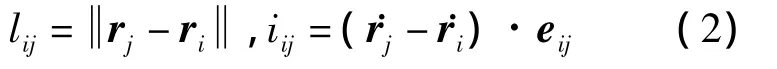
式中e ij為由節點i指向節點j的單位矢量。

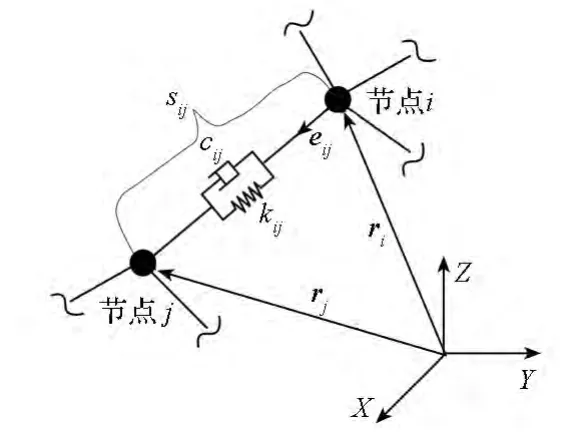
圖5 繩段sij的張力Fig.5 Tension on the segment sij

1.3 繩段單元外力計算

在空間環境下，繩段受萬有引力作用，由于大氣稀薄，氣動力可忽略不計，而且由于空間繩網展開過程較快，地球非球形攝動等干擾力也可忽略不計。由此作用于繩段sij的外力F exij為

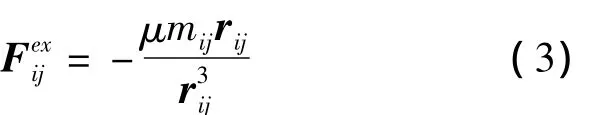
式中r ij為慣性系下繩段sij中心的位置矢量。

在地面環境下，作用于繩段的外力主要包括重力和氣動力等，而且氣動力可以分解為氣動阻力和氣動升力，如圖6所示，作用于繩段sij的外力為

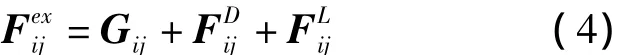
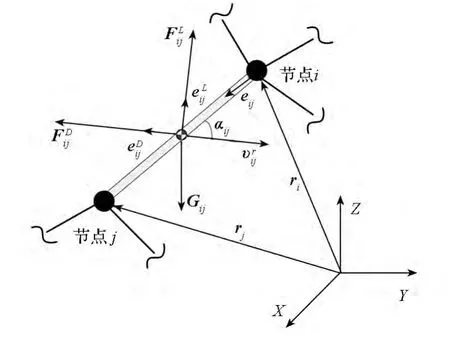
圖6 地面環境下作用于sij的外力Fig.6 Outside force on the segment sij on the ground

設地面重力加速度為g，則重力G ij可表示為

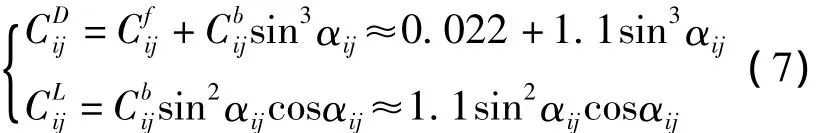
式中αij為sij的攻角。

1.4 系統動力學方程

不論是在地面環境，還是在空間環境，節點i的動力學方程都可以在地心慣性系下表示為

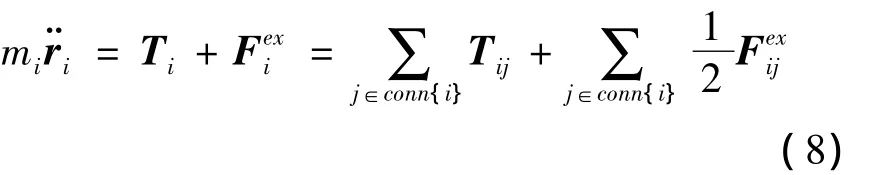
為了便于描述空間環境下的空間繩網展開特性，需要建立空間繩網在拖船軌道系下的相對運動動力學方程。由于拖船運行于圓軌道，由C-W方程，節點i在拖船軌道系下的相對運動方程為

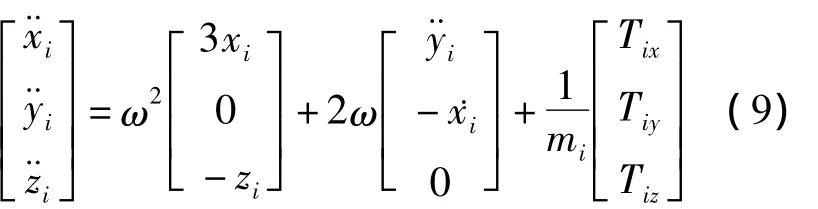
2 空間繩網展開過程仿真分析

2.1 性能參數定義

影響空間繩網展開性能的參數主要有展開面積和飛行距離，下面給出它們的定義。

展開面積可用于描述繩網覆蓋范圍，它決定了空間繩網可捕獲目標的尺寸。由于繩網的柔性，展開過程的形狀并不規整。對于正方形繩網，展開面積S可以由空間繩網四個頂點所圍成的四邊形ABCD的面積來表示，如圖7所示，d DA，d CB分別為四邊形兩條對角線的矢量，則展開面積S可由式(10)近似計算。

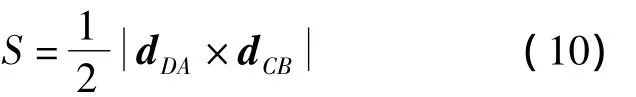
飛行距離是指空間繩網與拖船之間的相對距離，可以表征空間繩網的捕獲半徑。對于正方形繩網，飛行距離d可以由拖船到空間繩網四個頂點的中心的距離來表示。設拖船到四個頂點的位置矢量分別為d A，d B，d C，d D，則空間繩網四個頂點的中心On的位置矢量為

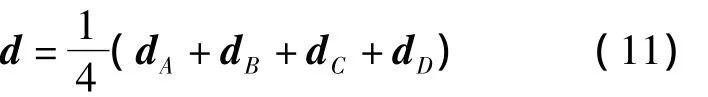
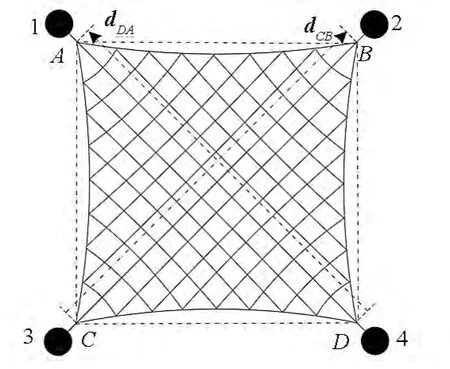
圖7 展開面積示意圖Fig.7 Sketch map of the deployment area

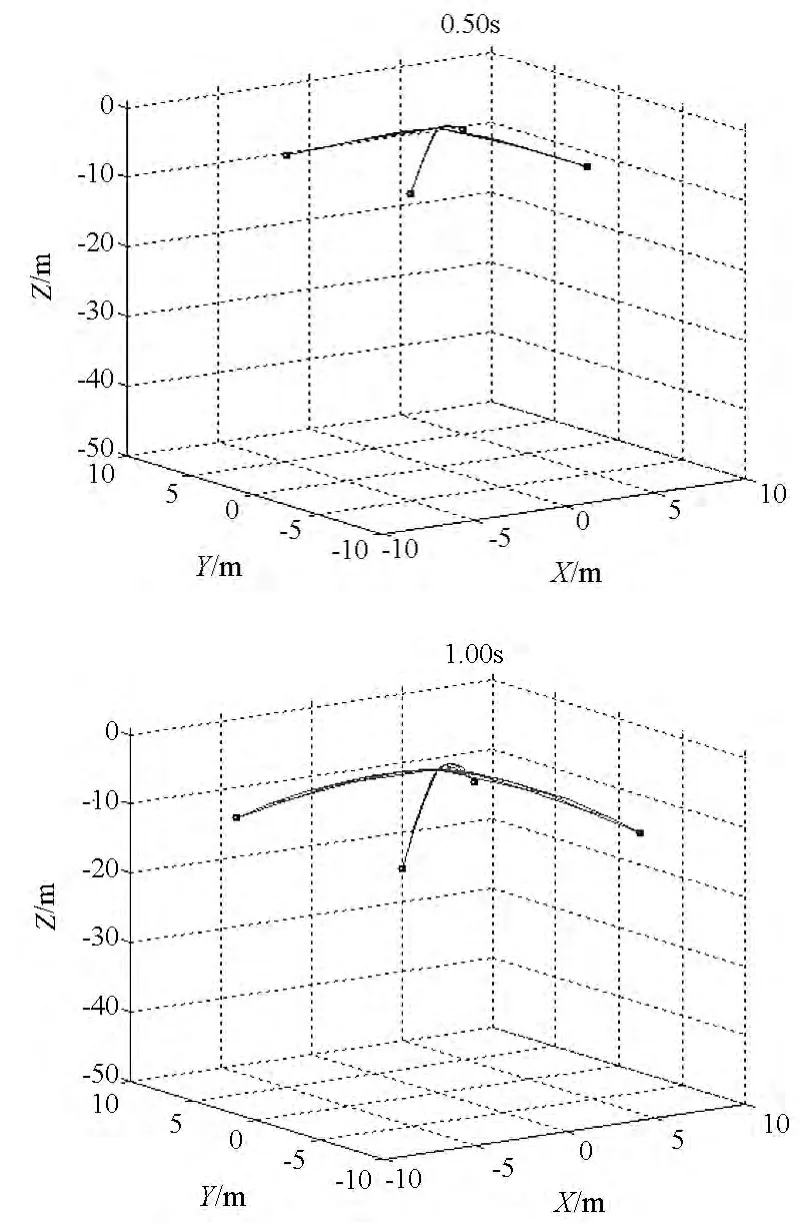
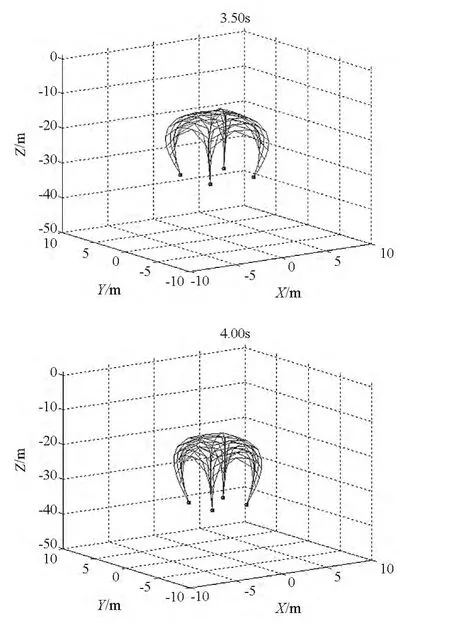
圖8 空間繩網地面試驗仿真圖Fig.8 Simulation diagram of ground test of the space web

2.2 地面試驗驗證

作者近年來進行了大量的地面試驗［10，17］，并通過試驗數據校核，改進了空間繩網動力學模型。下面以某次空間繩網地面試驗為例，對比試驗過程與仿真模型。地面試驗采取空中投放的方式，試驗中繩網系統從高空豎直向下發射，這樣可以有較長時間完成空間繩網展開。仿真參數根據試驗參數選取，動力學模型中考慮了空氣阻力和重力等外力。

空間繩網地面試驗的仿真過程如圖8所示，展開面積的試驗值與仿真值對比如圖9所示，飛行距離的試驗值與仿真值對比如圖10所示。可以看出，在地面環境下，空間繩網在質量塊的牽引下由“+”字形拉出并逐漸展開，在空氣阻力和重力作用下，空間繩網呈“降落傘”形狀下落。在試驗中展開面積的最大值為176.0 m2，在仿真中展開面積最大值為177.2 m2，兩者都遠遠小于空間繩網的設計面積(此處為40 m×40 m)，可見地面環境下空間繩網無法完全展開。在試驗與仿真中，展開面積與飛行距離的變化規律基本相似，數值誤差也都很小，這充分證明了地面環境下動力學模型的可靠性，也間接說明了空間環境下動力學模型的可靠性。

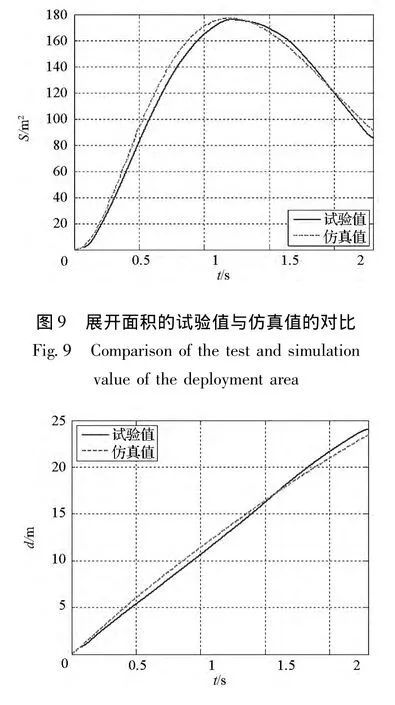
圖10 飛行距離的試驗值與仿真值的對比Fig.10 Comparison of the test and simulation value of the flying distance

2.3 空間繩網展開動力學特性

下面研究空間環境下的空間繩網展開過程。假設目標位于GEO軌道，拖船位于目標V-bar方向，繩網為邊長40 m的正方形繩網。繩網材料為Zylon?纖維，網目尺寸為Lmesh=0.404 1 m，編織繩索的線密度為0.247 5 g/m，由此編織而成的繩網質量為mw=2 kg。此外，單個質量塊質量為ms=1.5 kg，發射速度為υ=15 m/s，發射張角為α=30°，繩索阻尼比為ζ=0.5。

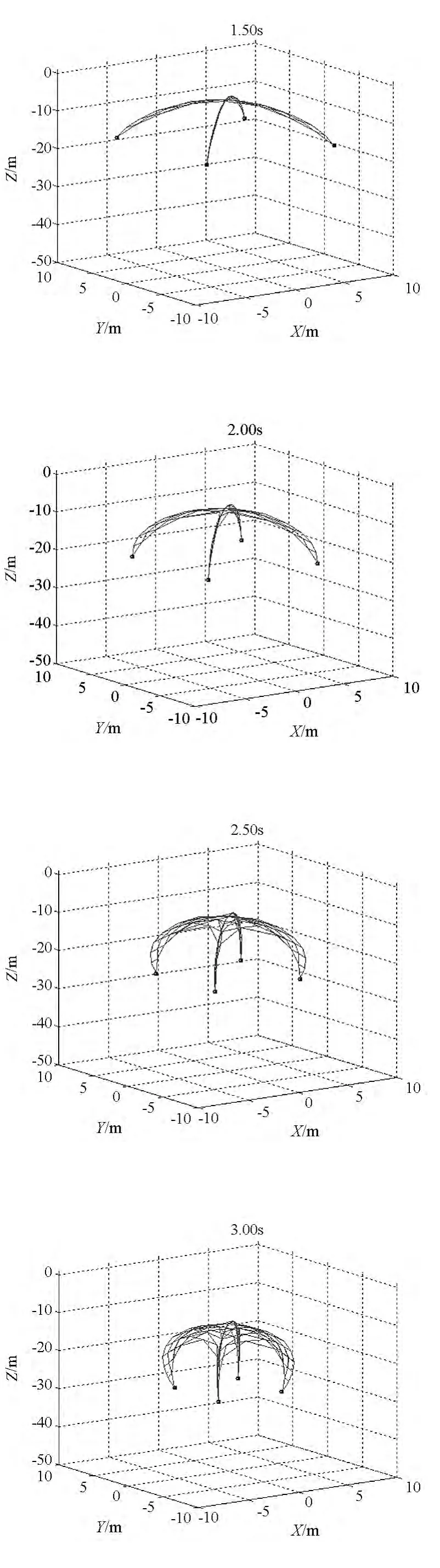
空間繩網展開的過程如圖11所示，圖中柱條表示繩段張力大小，單位為N。從圖中可以看出，在質量塊的牽引作用下，空間繩網沿對角線呈“+”字形拉出并逐漸展開成面狀，展開面積不斷變大，此時空間繩網幾何構型呈凹形。在一定時刻展開面積達到最大，整個空間繩網幾乎在一個平面上。在此之后，由于繩網具有彈性，質量塊和網面將發生收縮回彈，展開面積不斷變小，而且空間繩網中部的節點將超越質量塊向前運動，此時空間繩網幾何構型呈凸形。展開面積與飛行距離的變化曲線如圖12、圖13所示，可以看出展開面積先增大后減小，在圖中“〇”處達到最大值，此時飛行時間為5.24 s，展開面積為1580 m2，約為設計面積的98.75%，說明展開效果極佳;飛行距離則隨時間不斷增加，當展開面積最大時，飛行距離為51.1 m。

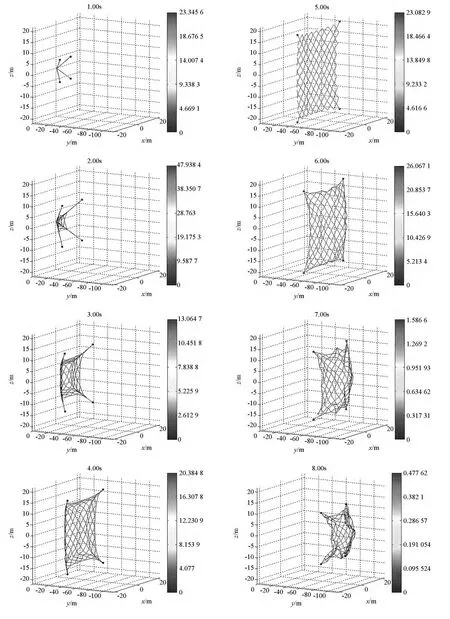
圖11 空間繩網展開過程圖Fig.11 Deploy course of the space web

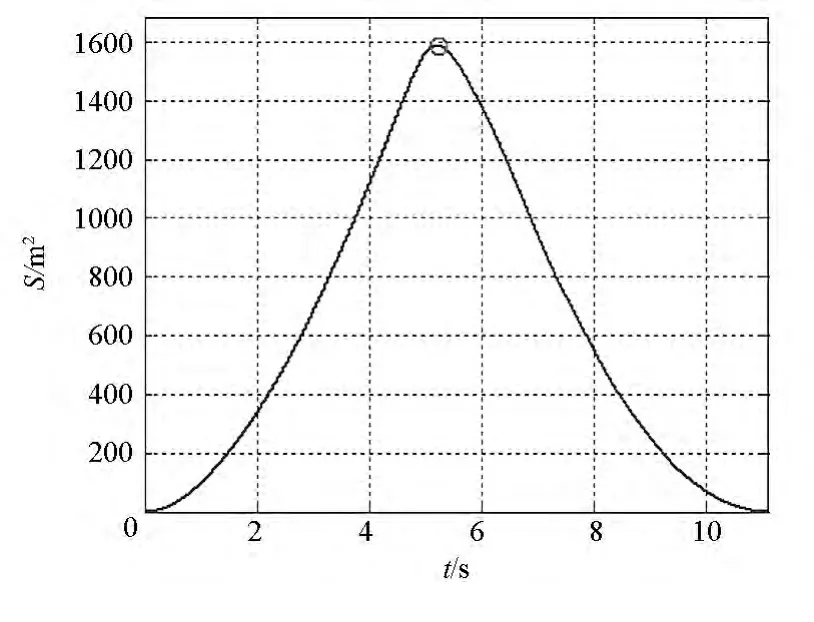
圖12 展開面積變化過程Fig.12 Change process of the deployment area

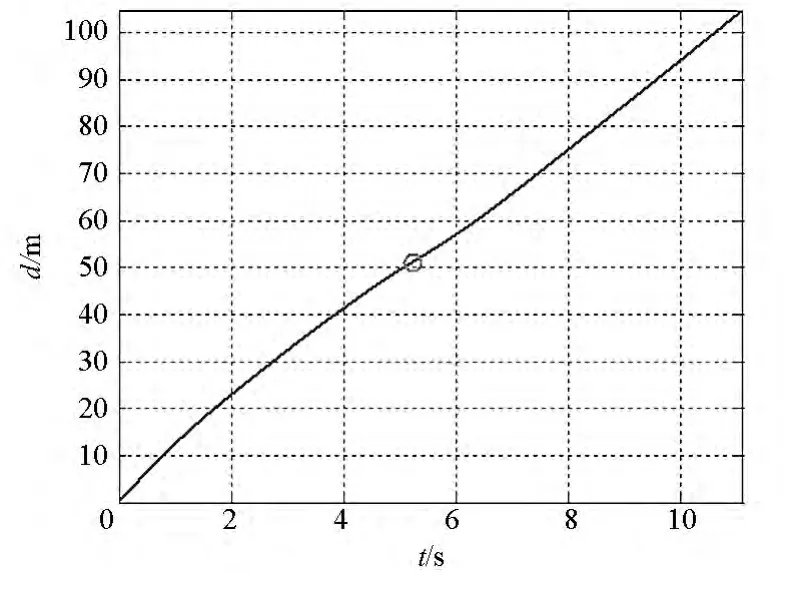
圖13 飛行距離變化過程Fig.13 Change process of the flying distance

空間繩網展開過程中的能量變化如圖14所示。可以看出，質量塊發射后，質量塊動能逐漸減小，繩網動能由0逐漸增大，在空間繩網完全展開前后質量塊動能達到最小值，繩網動能達到最大值;之后質量塊動能又逐漸增大，繩網動能逐漸減小。這一過程說明空間繩網展開過程中，質量塊與空間繩網之間發生著復雜的能量傳遞過程。系統的彈性勢能為繩網中所有繩段的彈性勢能之和，可以看出整個展開過程中，彈性勢能的量級都很小。系統總機械能為系統動能與彈性勢能之和，可以看出它始終呈下降趨勢，其原因是空間繩網的阻尼效應。

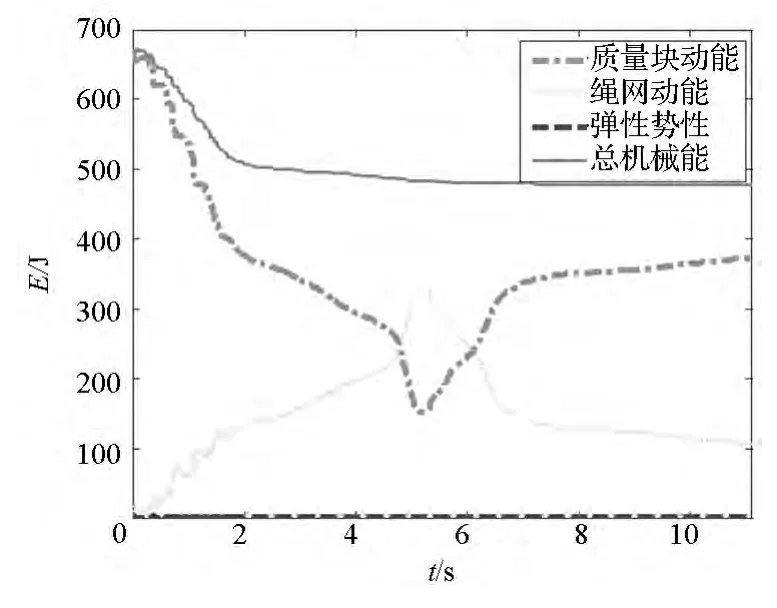
圖14 能量變化規律Fig.14 Change rule of the energy

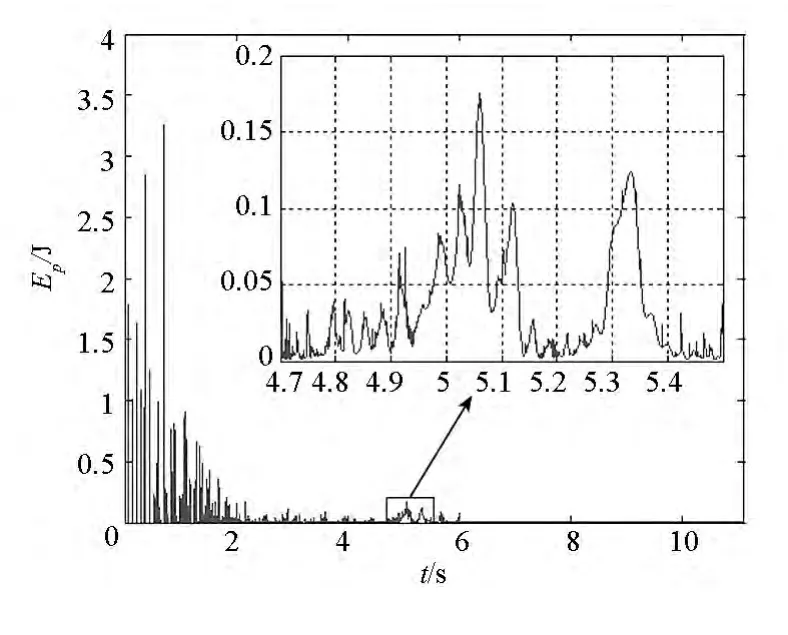
圖15 彈性勢能變化規律Fig.15 Change rule of the elastic potential energy

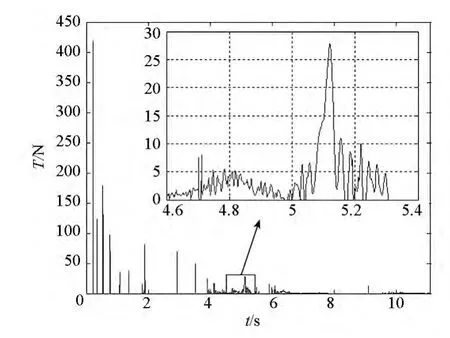
圖16 對角線上某繩段單元的張力Fig.16 Tension on the segment at the diagonal

圖15為單獨表示的彈性勢能曲線，圖16、圖17為兩個繩段單元的張力，這兩個繩段分別位于對角線和邊線，且與圖7所示的正方形頂點A相鄰。可以看出，起初彈性勢能成脈沖式變化規律，這是由于在質量塊牽引下，空間繩網中的繩段單元突然被拉緊，然后又迅速回彈，不停地經歷張緊與松弛的狀態變化，這時繩段單元張力的峰值很大，但作用時間很短;在空間繩網完全展開前后，彈性勢能的變化則相對平緩，這是由于此時空間繩網幾乎展開成一個平面狀(見圖11)，在四角的質量塊往外的拉力作用下，空間繩網內部的繩段單元有一個持續的張緊過程;在此之后，空間繩網彈性勢能更為微弱，這是由于空間繩網中的繩段單元處于長期松弛的狀態，而且張緊時張力的峰值也很小。

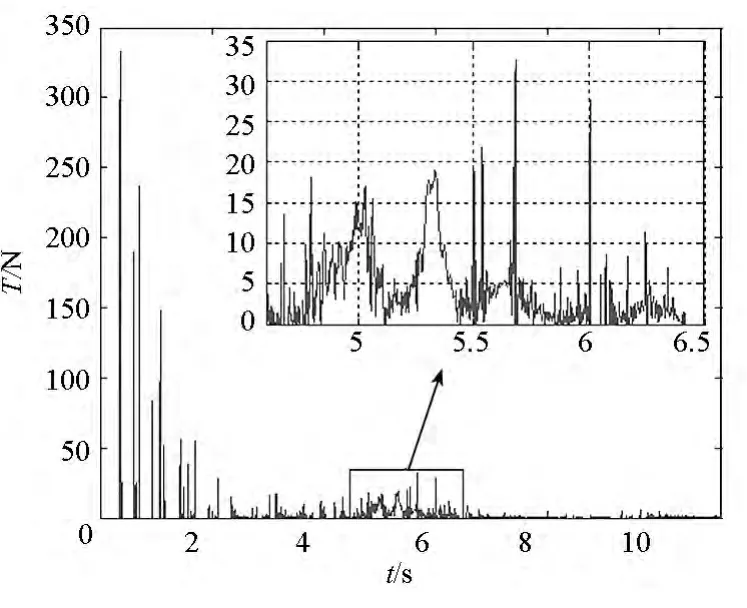
圖17 邊線上某繩段單元的張力Fig.17 Tension on the segment at the sideline

2.4 軌道高度與捕獲方向的影響

空間繩網在不同軌道高度以及不同捕獲方向下的展開效果是一個值得關注的問題。如果展開效果不受軌道高度的影響，則可說明空間繩網應用范圍的廣泛性;如果展開效果不受捕獲方向的影響，那么在捕獲時只需將發射軸線對準目標并發射繩網即可，不需另行調節其他參數就可以完成捕獲。下面分別就空間繩網在GEO、LEO軌道，沿V-bar、R-bar和H-bar這三個典型的捕獲方向的展開過程進行仿真研究。仿真中，GEO軌道半徑設為42 164 km，LEO軌道半徑設為7000 km，其他仿真參數不變。

圖18為不同軌道高度與捕獲方向的展開面積對比，圖19為不同軌道高度與捕獲方向的飛行距離對比。可以看出，在各種情況下，空間繩網展開過程的展開面積高度一致，飛行距離也高度一致。這說明軌道高度與捕獲方向對展開面積與飛行距離基本沒有影響。

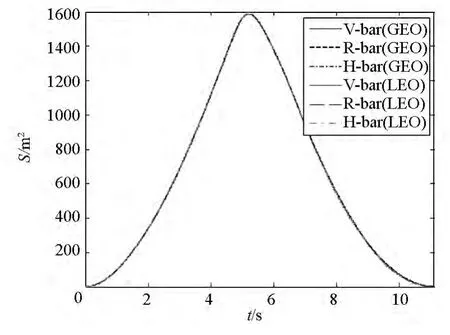
圖18 不同軌道高度與捕獲方向的展開面積Fig.18 Deployment area of different orbit height and capture direction

盡管軌道高度與捕獲方向不影響展開面積與飛行距離，但是由于軌道動力學的作用，不同的軌道高度與捕獲方向可能使得空間繩網飛行過程中偏離發射軸線的程度不一樣。定義空間繩網在飛行過程中，相對于發射軸線方向的偏移為橫向偏移，如果橫向偏移過大有可能影響空間繩網成功捕獲目標。對于正方形繩網，橫向偏移Dax可以由空間繩網四個頂點的中心On到發射軸線的距離來表示，On的位置矢量由式(11)求得，Dax由點到直線的距離公式計算得到。

圖19 不同軌道高度與捕獲方向的飛行距離Fig.19 Flying distance of different orbit height and capture direction

圖20、圖21分別表示GEO軌道和LEO軌道下，不同捕獲方向的橫向偏移。可以看出，橫向偏移隨著時間大致成指數級增長，而且受捕獲方向的影響較為明顯，捕獲方向為V-bar和R-bar時空間繩網的橫向偏移比捕獲方向為H-bar時的要大。V-bar捕獲時，GEO軌道下空間繩網完全展開時(5.24 s)的橫向偏移僅為毫米級，而LEO軌道下為分米級。但是，由于空間繩網完全展開后尺寸高達40 m，而且設計時考慮了對目標捕獲的冗余度，因此空間繩網捕獲完全能夠承受這一量級的橫向偏移，這體現了繩網捕獲的容錯性這一優勢。

圖20 不同捕獲方向的橫向偏移(GEO)Fig.20 Transverse offset in different capture direction(GEO)

圖21 不同捕獲方向的橫向偏移(LEO)Fig.21 Transverse offset in different capture direction(LEO)

2.5 發射參數的影響

影響繩網展開性能的發射參數有發射速度和發射張角，合理選擇發射參數對于捕獲任務的實施至關重要。

發射速度分別取10 m/s，15 m/s和20 m/s，發射張角都取30°，其他仿真參數不變，仿真得到展開面積與飛行距離如圖22、圖23所示，圖中“〇”對應著展開面積達到最大的時刻。

圖22 不同發射速度的展開面積Fig.22 Deployment area in different casting velocity

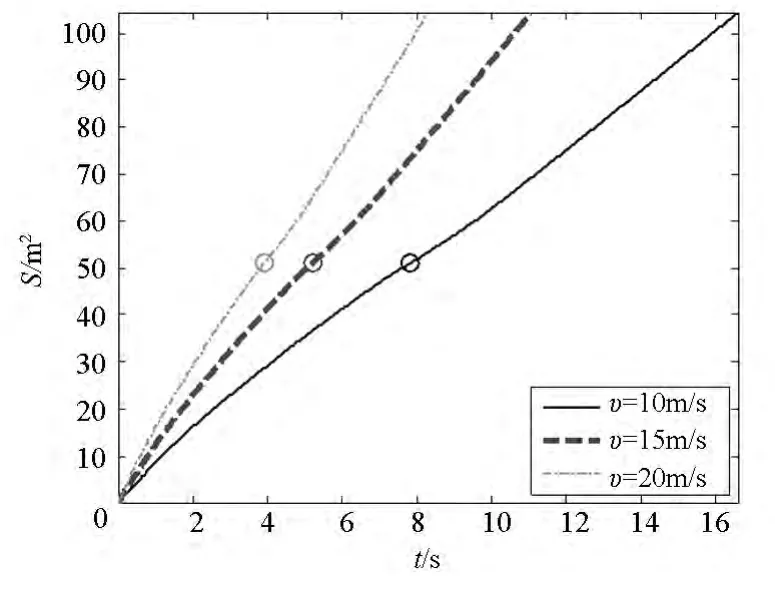
圖23 不同發射速度的飛行距離Fig.23 Flying distance in different casting velocity

可以看出，不同的發射速度對展開面積的最大值以及展開面積最大時的飛行距離幾乎沒有影響;但發射速度越大，達到最大展開面積的時間越短。

發射張角分別取20°，30°和40°，發射速度都取15 m/s，其他仿真參數不變，仿真得到展開面積與飛行距離如圖24、圖25所示，圖中“〇”對應著展開面積達到最大的時刻。可以看出，不同的發射張角對展開面積的最大值幾乎沒有影響;但發射張角越大，達到最大展開面積的時間越短，而且展開面積最大時的飛行距離越小。

綜上可知，不同的發射速度與發射張角對最大展開面積幾乎沒有影響;但是較大的發射速度與較大的發射張角有利于繩網快速展開，較小的發射張角有利于增大繩網捕獲距離。

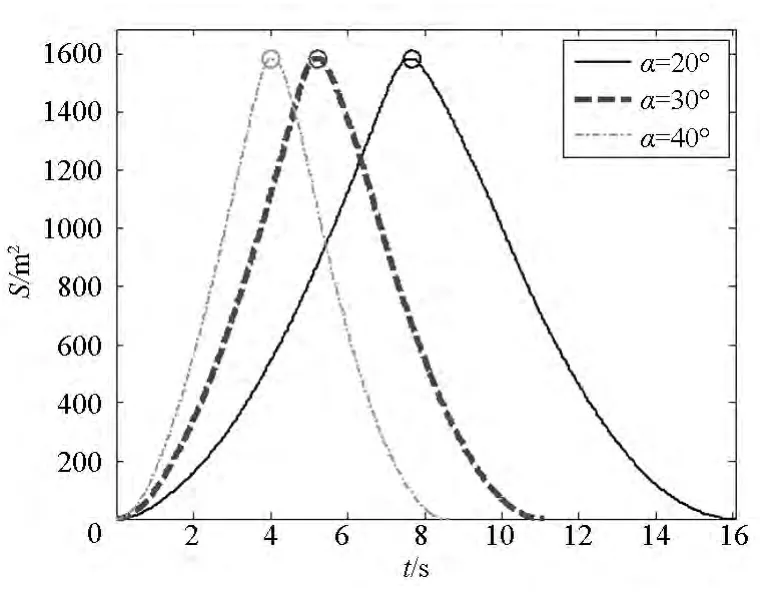
圖24 不同發射張角的展開面積Fig.24 Deployment area in different casting angle

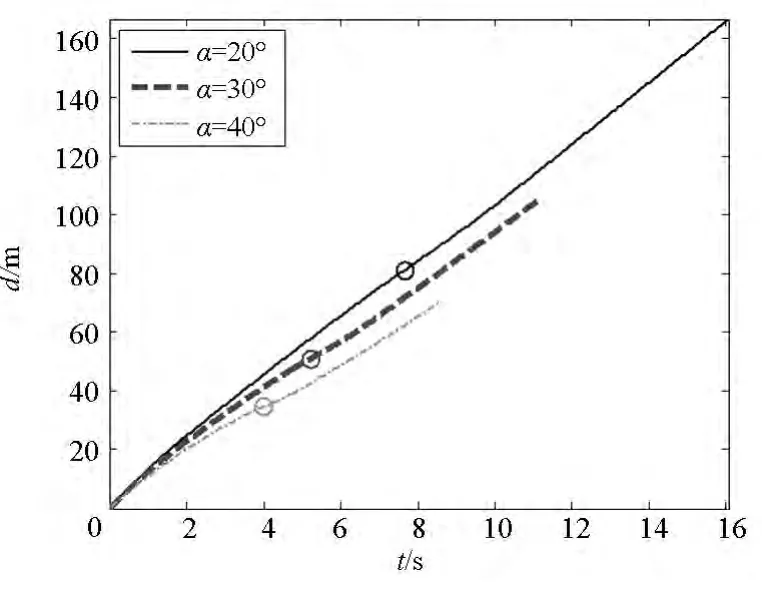
圖25 不同發射張角的飛行距離Fig.25 Flying distance in different casting angle

3 結論

采用離散化的建模思路，推導了空間繩網動力學模型;通過地面試驗驗證了動力學仿真模型的有效性;通過仿真，分析了空間繩網展開過程中的動力學特性。

繩網展開過程中，展開面積先逐漸增大，達到最大值后由于彈性發生網面收縮回彈;系統總機械能由于阻尼效應始終呈下降趨勢;系統彈性勢能的量級很小，而且一直處于劇烈波動狀態，這是由于繩網中的繩段單元一直在不斷經歷張緊與松弛的狀態變化。軌道高度和捕獲方向不會影響展開面積與飛行距離的變化，但是會產生不同的橫向偏移，在LEO軌道能達到分米量級，但由于繩網尺寸的冗余性設計，使得繩網捕獲依然有效，體現了繩網捕獲容錯性的優勢。發射速度與張角影響繩網展開性能，較大的發射速度與張角有利于繩網快速展開，較小的發射張角有利于增大繩網捕獲距離，可在下一步研究中尋找使展開效果達到最優的發射參數組合。

References)

［1］Bremen A S.Robotic geostationary orbit restorer(ROGER)phase a final report［R］.European Space Agency，2003.

［2］Liu H T，Yang L P，Zhang Q B，et al.An investigation on tether-tugging de-orbit of defunct geostationary satellites［J］.Science China Technological Sciences，2012，55(7):2019-2027.

［3］Tibert G，G?rdsback M.Space webs final report［R］.European Space Agency，2006.

［4］Grossman J.Solar sailing:the next space craze?［J］.Engineering and Science，2000，63(4):18-29.

［5］Nakasuka S，Kaya N.Quick release on experiment results of mesh deployment and phased array antenna by S-310-36［J］.The Forefront of Space Science，2006.

［6］Mankala K K，Agrawal S K.Dynamic modeling and simulation of impact in tether net/gripper systems［J］.Multibody System Dynamics，2004，11(3):235-250.

［7］Zhai G，Qiu Y，Liang B，et al.Research of capture error and error compensate for space net capture robot［C］//Proceedings of the IEEE International Conference on Robotics and Biomimetics，Sanya，China，2007:467-472.

［8］Zhai G，Qiu Y，Liang B，et al.On-orbit capture with flexible tether-net system［J］.Acta Astronautica，2009，65(5-6):613-623.

［9］陳欽，楊樂平.空間繩網系統發射動力學問題研究［J］.宇航學報，2009，30(5):1829-1833.CHEN Qin，YANG Leping.Research on casting dynamics of orbital net systems［J］.Journal of Astronautics，2009，30(5):1829-1833.(in Chinese)

［10］陳欽，楊樂平，張青斌.空間飛網發射動力學建模仿真研究與地面試驗［J］.國防科技大學學報，2009，31(3):16-19.CHEN Qin，YANG Leping，ZHANG Qingbin.Dynamic model and simulation of orbital net casting and ground test［J］.Journal of National University of Defense Technology，2009，31(3):16-19.(in Chinese)

［11］陳欽.空間繩網系統設計與動力學研究［D］.長沙:國防科學技術大學，2010.CHEN Qin.Design and dynamics of an orbital net-capture system［D］.Changsha:National University of Defense Technology，2010.(in Chinese)

［12］于洋，寶音賀西，李俊峰.空間飛網拋射展開動力學建模與仿真［J］.宇航學報，2010，31(5):1289-1296.YU Yang，BAOYIN Hexi，LI Junfeng.Modeling and simulation of projecting deployment dynamics of space webs［J］.Journal of Astronautics，2010，31(5):1289-1296.(in Chinese)

［13］李京陽，于洋，寶音賀西，等.空間飛網兩種動力學模型的比較研究［J］.力學學報，2011，43(3):542-550.LI Jingyang，YU Yang，BAOYIN Hexi，et al.Simulation and comparison of different dynamical models of space webs［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(3):542-550.(in Chinese)

［14］Yu Y，Baoyin H X，Li J F.Dynamic modelling and analysis of space webs［J］.SCIENCE CHINA Physics，Mechanics＆Astronomy，2011，54(4):783-791.

［15］馬駿，黃攀峰，孟中杰，等.自主機動空間繩網機器人設計與動力學建模［J］.宇航學報，2013，34(10):1316-1322.MA Jun，HUANG Panfeng，MENG Zhongjie，et al.Design and dynamics modeling of autonomous maneuvering tetherednet space robot system［J］.Journal of Astronautics，2013，34(10):1316-1322.(in Chinese)

［16］Liu H T，Zhang Q，Yang L，et al.Modeling and simulation of deployment dynamics of space webs［C］//Proceedings of the 64th International Astronautical Congress，Beijing，China，2013:2628-2635.

［17］張青斌，孫國鵬，豐志偉，等.柔性繩網動力學建模與天地差異性分析［J］.宇航學報，2014，35(8):871-877.ZHANG Qingbin，SUN Guopeng，FENG Zhiwei，et al.Dynamics modeling and differentia analysis between space and ground for flexible cable net［J］.Journal of Astronautics，2014，35(8):871-877.(in Chinese)

［18］Williams P.Optimal wind power extraction with a tethered kite［C］//Proceedings of the AIAA Guidance，Navigation，and Control Conference，Keystone，Colorado，2006.

［19］Williams P，Sgarioto D，Trivailo P.Optimal control of an aircraft-towed flexible cable system［J］.Journal of Guidance，Control and Dynamics，2006，29(2):401-410.