零控脫靶量有限時間收斂制導律*

雷虎民，張 旭，董飛垚，李 炯

(1.空軍工程大學防空反導學院，陜西西安710051;2.中國人民解放軍95437部隊，四川彭山620864)

近年來，隨著全球空間競爭的日趨激烈，高速機動飛行器的研究受到各國的普遍重視并得到了相當程度的發展，目前，一些高超聲速飛行器已經投入軍事應用，給各國導彈防御系統帶來了嚴峻的挑戰。

在新的攔截情形下，由于彈目相對速度很大，末制導攔截時間又很短，這就對攔截導彈的精確制導技術研究提出了特別的要求［1-3］。文獻［1］研究了使視線角速率有限時間收斂的多種高精度制導方法，以滿足新一代導彈實現“趨零脫靶量”精確制導能力的要求，取得了良好的制導效果;文獻［2］基于Lyapunov穩定性理論分別設計了導彈俯仰平面和偏航平面的視線角速率有限時間收斂制導律，該制導律既能保證系統有限時間穩定，又能夠保證其有限時間收斂;文獻［3］基于新型自適應非奇異Terminal滑模控制方法，設計了一種部分制導與控制一體化有限時間收斂控制算法，可保證滑模面在有限時間內收斂到零。同時，為了使導彈能夠更好地適應新型攔截的實際需要，考慮導彈自動駕駛儀動態特性的制導律也得到了廣泛的研究［1，4-10］。文獻［4-5］分別考慮導彈自動駕駛儀一階和二階動態特性，設計了變結構制導律，但不能使導彈的視線角速率在有限時間內收斂到零;文獻［6］運用非線性反步設計法，設計了考慮自動駕駛儀動態特性的終端角度約束滑模導引律，并能夠保證導彈的有限時間收斂特性;文獻［7］基于有限時間穩定性理論，設計了考慮導彈自動駕駛儀動態特性的有限時間收斂制導律，具有較強的魯棒性;文獻［8-9］通過引入低通濾波器，運用動態面控制方法，設計了考慮導彈自動駕駛儀二階動態特性的制導律;文獻［10］為改善BTT導彈的捕獲區性能，設計了考慮導彈自動駕駛儀動態特性的最優制導律，仿真實驗證明了其有效性和實用性。文獻［11］根據平行接近法原理推導了一種動能攔截器零控脫靶量制導律，具有較高的制導精度;文獻［12］設計了基于零控脫靶量的大氣層外超遠程攔截制導律;但是這兩種制導律只能使零控脫靶量在攔截結束時刻收斂到零，不能使零控脫靶量在有限時間內收斂到零。

1 零控脫靶量三維制導模型推導

零控脫靶量的具體表達式有多種形式，對零控脫靶量的定義如下:從當前時刻開始，導彈的制導指令為零，目標按照當前的機動狀態繼續飛行，最終獲得的彈目之間的最小距離。導彈-目標三維相對運動學關系如圖1所示。

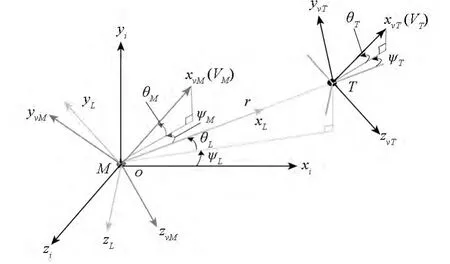
圖1 導彈-目標三維相對運動學關系Fig.1 Three-dimensional relative motion geometry of missile and target

圖1中:M為導彈，T為目標，r為彈目相對距離;oxi yi zi為慣性坐標系，oxL yL zL為視線坐標系;θT和ψT為目標的彈道傾角和彈道偏角;θM和ψM為導彈的彈道傾角和彈道偏角;θL和ψL為視線傾角和視線偏角。由圖1所示的彈目三維相對運動學關系，可得如下彈目運動方程:

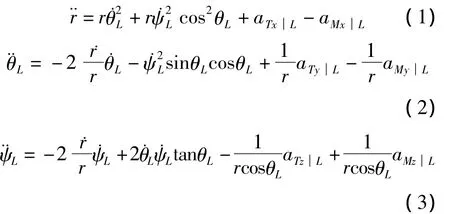
由于重點對導彈攔截目標的末制導段進行研究，可假定導彈中制導結束后，導彈-目標初始對準良好，且整個飛行過程中彈目視線角變化不大［13］。因此，選擇以導彈-目標初始視線坐標系oxL0yL0zL0為基準，將三維非線性彈目攔截幾何關系解耦為俯仰平面和偏航平面進行單獨研究。首先對俯仰平面內的彈-目攔截問題進行研究，如圖2所示。

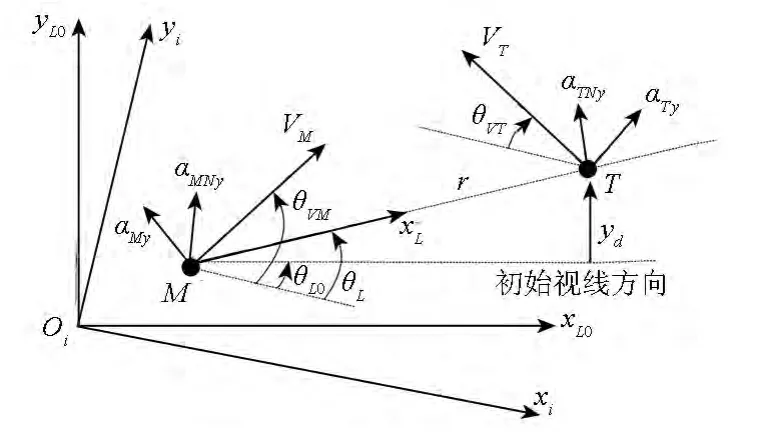
圖2 俯仰平面內的彈目相對幾何關系Fig.2 Relative motion geometry of missile and target in pitch plane

令ψL=180°，˙ψL=0，則式(1)和(2)可轉化為:

式中，Vr和Vy⊥分別為彈目相對速度沿視線方向和垂直視線方向分量。根據幾何關系，其表達式如下所示:

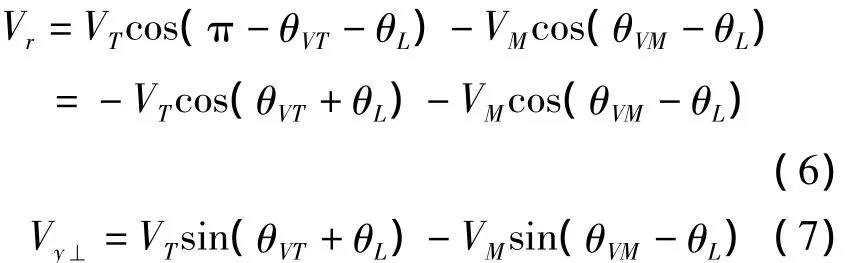
假定在制導末端，導彈和目標的速度大小變化不大，近似認為是常值，則剩余飛行時間tgo可近似由式(8)確定:

令yd，aTNy和aMNy表示r，aT和aM沿初始視線坐標系y方向的分量，則有:

由于在導彈攔截目標的過程中，彈目視線角變化不大［13］，故有:

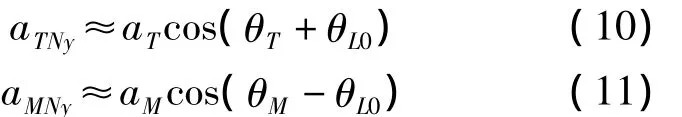
式中，θL0為彈目初始視線傾角。

為了更加符合實際作戰情形，將目標和導彈的動態特性分別視為時間常數為τT和τM的一階慣性環節，即:

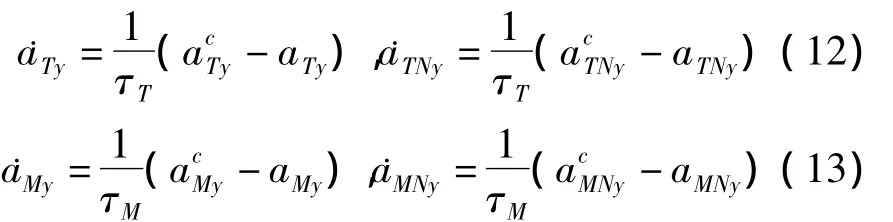
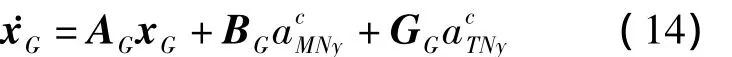
根據零控脫靶量的定義，得俯仰平面內導彈的零控脫靶量yZEM為:

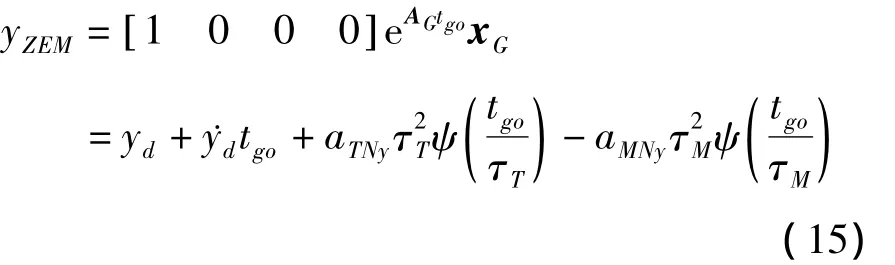
式中，ψ(ξ)=e-ξ+ξ-1，eAGtgo為式(14)關于剩余飛行時間tgo的狀態轉移矩陣，其表達式為:

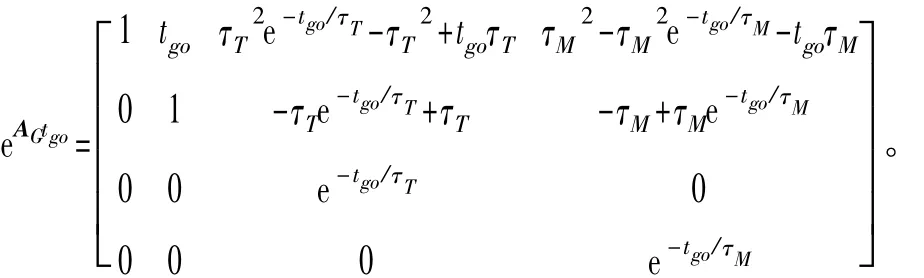
考慮信息的可獲取性，對式(15)進行重新整理和化簡。根據圖2描述的幾何關系有:

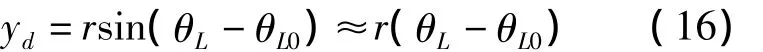
對式(16)兩端求導，可得:

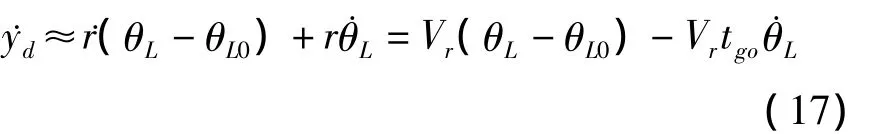
對式(17)兩端同時乘以tgo并結合式(16)，可得:

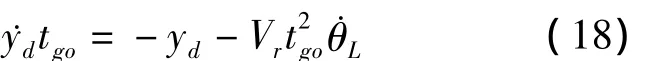
將式(18)代入式(15)，可得:

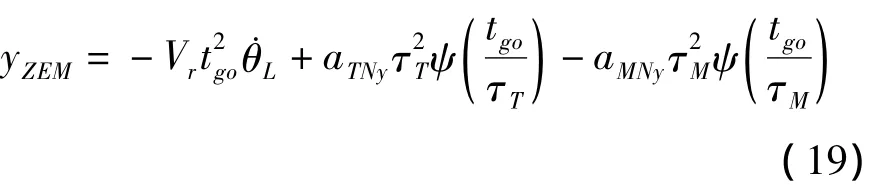
同理，可得偏航平面的零控脫靶量zZEM為:

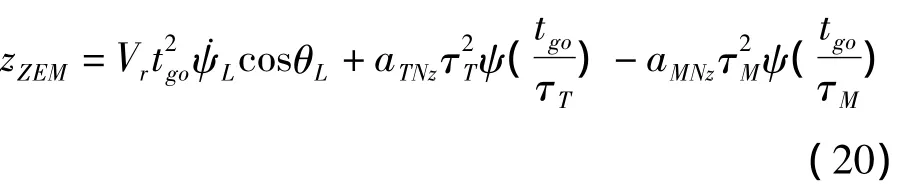
式中，aTNz和aMNz分別表示aT和aM沿初始視線坐標系z方向的分量。

2 零控脫靶量有限時間收斂制導律設計

2.1 制導律設計

根據零控脫靶量的定義，零控脫靶量是當導彈的制導指令為零，目標按照當前的機動狀態繼續飛行時，所獲得的彈目之間的最小距離。因此，若yZEM和zZEM到達并保持到零附近的鄰域內，就能夠保證導彈-目標的最終脫靶量為零，從而確保導彈準確命中目標。又的相對階為1，因此可直接選擇yZEM為滑模變量:

為了便于后續推導，對式(6)～(8)求導并結合式(2)，可得:

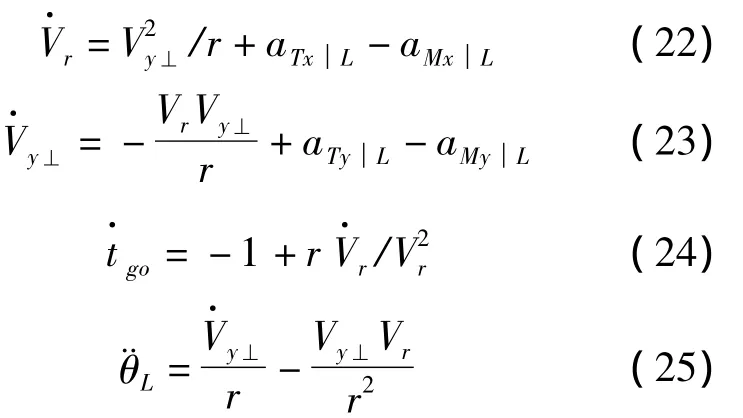
結合式(19)、式(24)和式(25)，可得

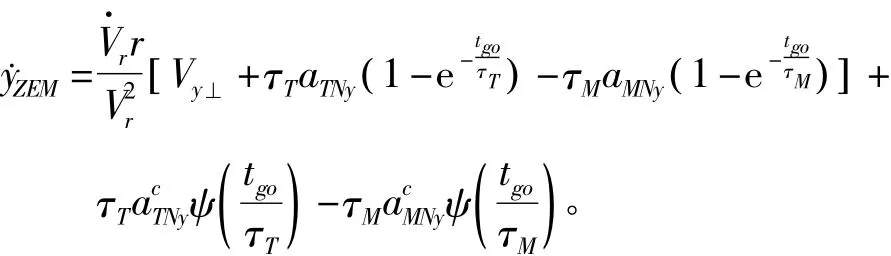
證明:由于導彈在攔截目標的過程中，彈目距離不斷減小，因此剩余飛行時間也逐漸趨向于零，即

由此，俯仰平面和偏航平面的制導律可設計如下:

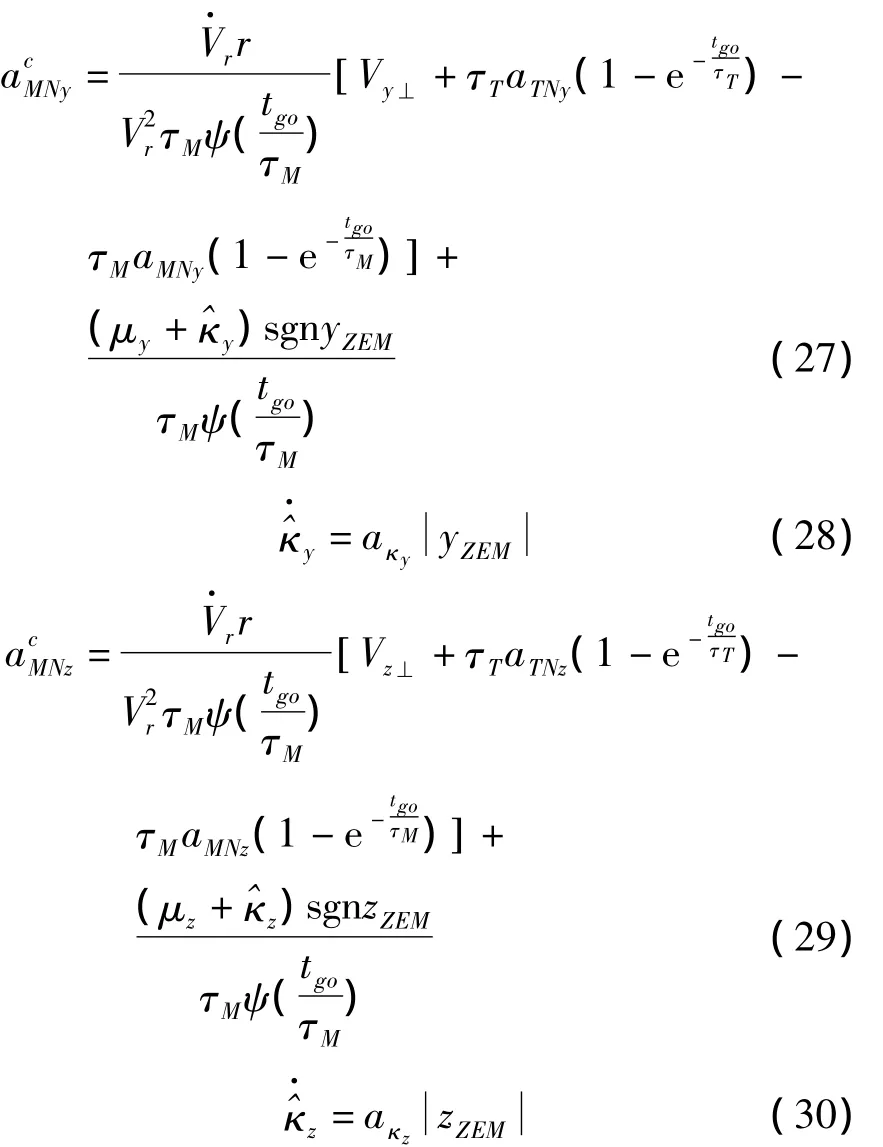
式中，μy，μz為大于零的常數，aκy，aκz為自適應因子。

同時，為了克服普通滑模帶來的抖振現象，采用如下飽和函數sat(·)代替符號函數sgn(·):

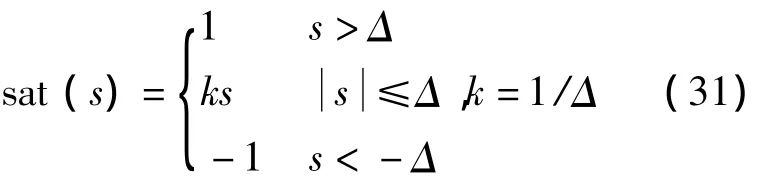
式中，Δ為邊界層厚度。

2.2 穩定性分析

選擇如下Lyapunov函數:

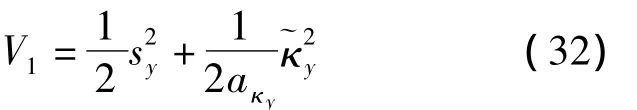
對式(32)兩端求導，并結合式(26)，可得:

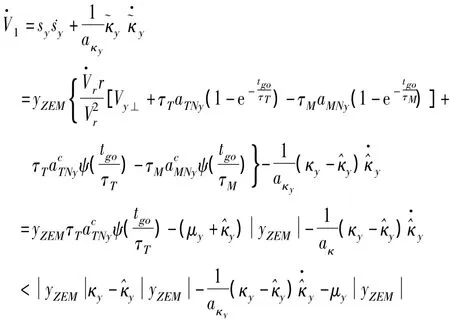
因此，穩定性得證。同理，可證明式(29)～(30)所示的偏航平面的零控脫靶量有限時間收斂制導律亦能保證系統Lyapunov穩定。

2.3 有限時間收斂特性分析

該制導律設計的目的，就是在考慮導彈自動駕駛儀動態特性的前提下，設計導彈視線角速率有限時間收斂制導律。因此需要對其有限時間收斂特性進行分析，首先給出如下引理［14］。

引理針對自治系統˙x=f(x)，f(0)=0，假設存在連續光滑可微函數V2(x):U→R，使其滿足如下條件:

1)V2(x)為正定函數。

2)存在實數c〉0和κ∈(0，1)，以及一個定義在原點的鄰域U0∈U，使得下列條件成立:

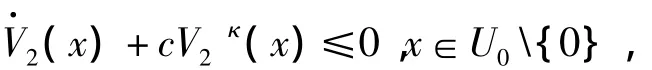
則上述自治系統是有限時間穩定的;若U=U0=Rn，則該自治系統為全局有限時間穩定。

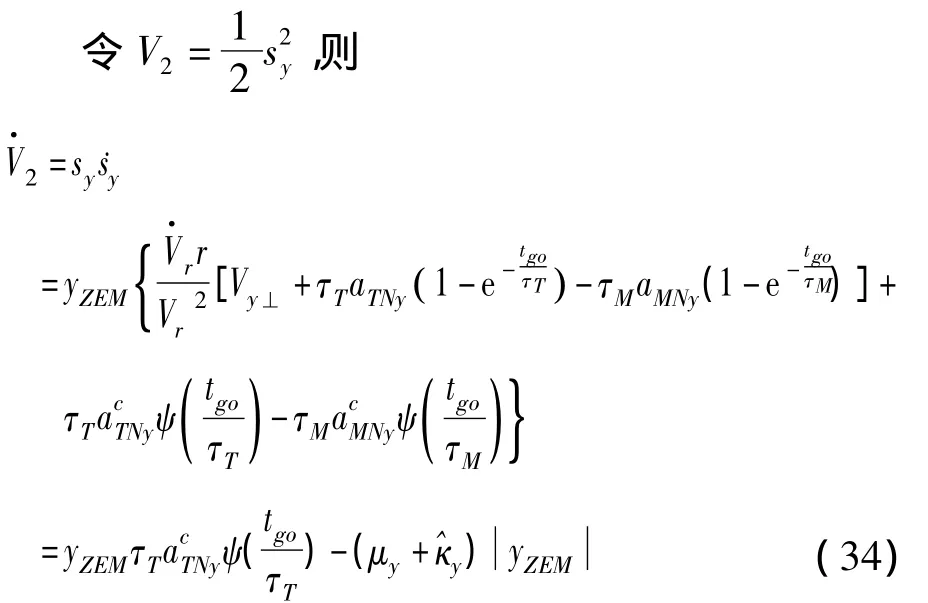
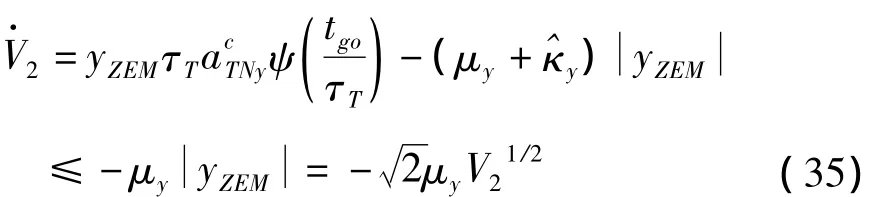
由于采用飽和函數法對制導律的繼電特性進行了連續化，因此會對系統的有限時間收斂特性產生一定的影響。如式(36)所示:

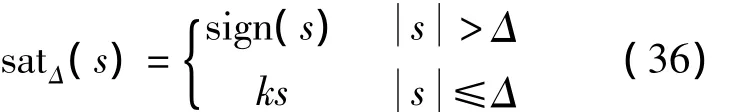
3 仿真結果分析

為驗證所設計的零控脫靶量有限時間收斂的自適應滑模制導律的有效性，在MATLAB下進行數字仿真，仿真步長為0.01s;但當彈目距離小于300m時，步長為0.01ms。導彈和目標初始參數設置如下:目標初始位置為(26 000m，21 000m，2000m)，速度為1800m/s，初始彈道傾角為170°，初始彈道偏角為0°，目標在俯仰和偏航平面內做正弦型機動，aty=aty0sin(πt/3)，atz=atz0sin(πt/3);由于目標機動加速度延遲時間常數無法測得，故令其機動時間常數為0.01s;導彈初始位置為(0m，19 000m，0m)，速度為1600m/s，初始彈道傾角為4.39°，初始彈道偏角為-4.40°。

此外，仿真中，將所設計的制導律與比例制導律進行對比分析，有效導航比為3.0，為突出考慮自動駕駛儀動態特性的制導律的優勢，自動駕駛儀時間常數取較大的0.45s，導彈的最大可用過載為20g;aκy=aκz=0.5，，μy=μz=0.5。為了便于描述，比例導引律用PNG表示，基于零控脫靶量有限時間收斂制導律用FZEM表示，仿真結果如圖3～5和表1所示。

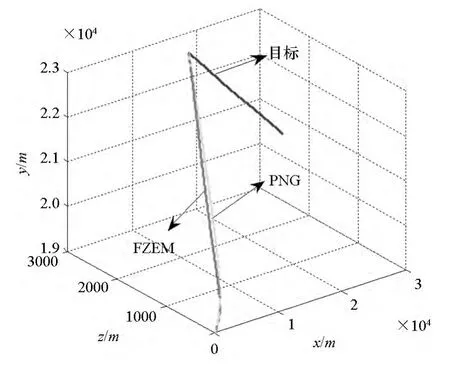
圖3 三維彈道軌跡Fig.3 Three-dimensional ballistic trajectories

由圖3～4可知，FZEM可保證導彈俯仰平面偏航平面內的零控脫靶量在有限時間內收斂到零，而PN只能保證零控脫靶量在導彈攔截目標結束時刻收斂到零。由圖5可知，在攔截初始階段，FZEM的過載大于PN的過載，此后FZEM的過載均小于PN，這主要是由于FZEM在攔截初始階段需要較大的過載，使零控脫靶量在有限時間內收斂到零;一旦零控脫靶量達到有限時間收斂，則其過載便會小于PN過載。由表1可知，在目標做不同形式和大小的機動時，FZEM均能夠以較小的脫靶量準確命中目標，而PN在aty0較大時，總是出現脫靶。因此，與比例制導律相比，零控脫靶量有限時間收斂制導律具有更高的制導精度，且可使零控脫靶量在有限時間內收斂到零。

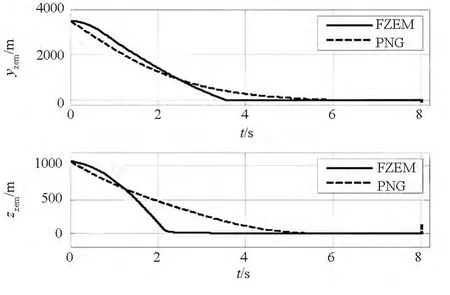
圖4 零控脫靶量隨時間變化曲線Fig.4 Time history of zero-effort miss

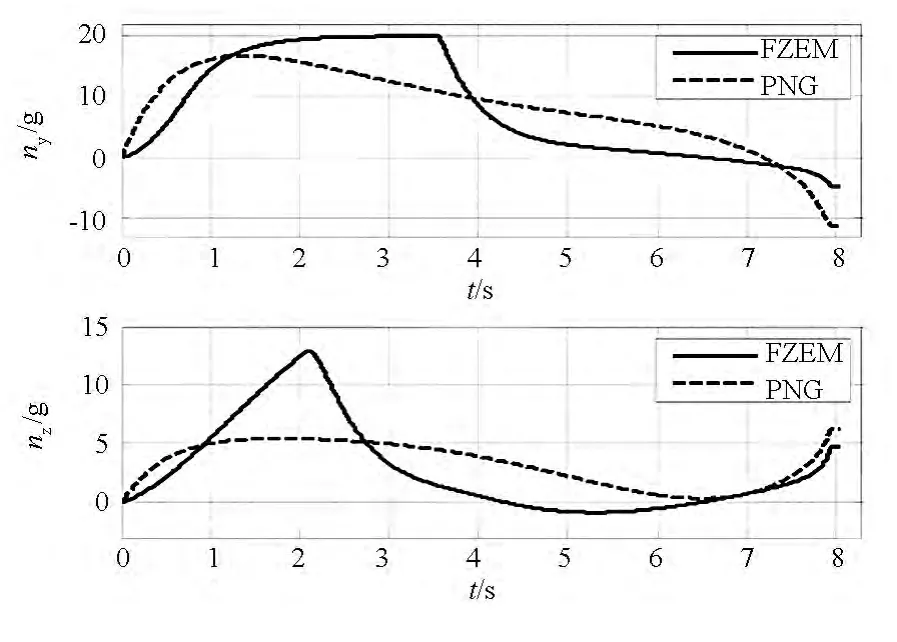
圖5 導彈過載隨時間的變化曲線Fig.5 Time history of missile overload

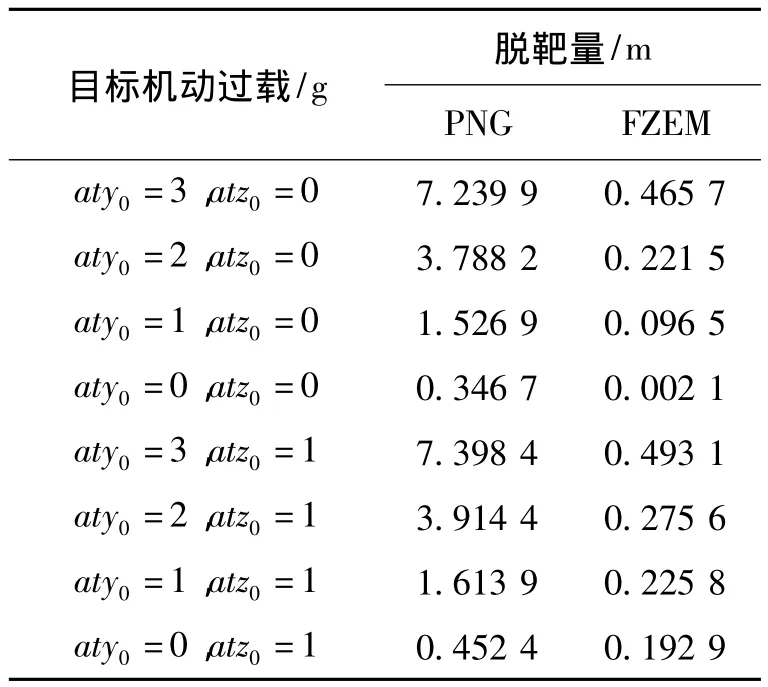
表1 不同制導律攔截性能比較Tab.1 Interception performance comparison between different guidance laws

4 結論

本文針對新型高速機動目標的攔截問題，將彈目三維攔截幾何關系解耦到俯仰平面和偏航平面，推導了考慮導彈自動駕駛儀動態特性的新型零控脫靶量制導模型;根據自適應滑模控制理論和有限時間穩定性理論，選取兩個平面的零控脫靶量為滑模面，設計了三維零控脫靶量有限時間收斂制導律;選取兩種不同的Lyapunov函數，對所設計制導律的穩定性和有限時間收斂進行了詳細地分析;通過與比例制導律進行仿真對比分析，表明該制導律具有良好的零控脫靶量有限時間收斂特性，且在目標做不同形式和大小的機動時，均能夠有效命中目標，并具有更高的制導精度。

References)

［1］孫勝.有限時間收斂尋的導引律［D］.哈爾濱:哈爾濱工業大學，2010.SUN Sheng.Guidance laws with finite time convergence for homing missiles［D］.Harbin:Harbin Institute of Technology，2010.(in Chinese)

［2］Zhou D，Sun S，Teo K L.Guidance laws with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1838-1846.

［3］Wang X H，Wang J Z.Partial integrated missile guidance and control with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2013，36(5):1399-1409.

［4］佘文學，周軍，周鳳岐.一種考慮自動駕駛儀動態特性的自適應變結構制導律［J］.宇航學報，2003，24(3):245-249.SHE Wenxue，ZHOU Jun，ZHOU Fengqi.An adaptive variable structure guidance law considering missile's dynamics of autopilot［J］.Journal of Astronautics，2003，24(3):245-249.(in Chinese)

［5］佘文學，周鳳岐，周軍.考慮自動駕駛儀動態魯棒自適應變結構制導律［J］.系統工程與電子技術，2003，25(12):1513-1516.SHE Wenxue，ZHOU Fengqi，ZHOU Jun.Robust adaptive variable structure guidance law considering autopilot dynamics［J］.Systems Engineering and Electronics，2003，25(12):1513-1516.(in Chinese)

［6］孫勝，張華明，周荻.考慮自動駕駛儀動特性的終端角度約束滑模導引律［J］.宇航學報，2013，34(1):69-78.SUN Sheng，ZHANG Huaming，ZHOU Di.Sliding mode guidance law with autopilot lag for terminal angle constrained trajectories［J］.Journal of Astronautics，2013，34(1):69-78.(in Chinese)

［7］Sun S，Zhou D，Hou W T.A guidance law with finite time convergence accounting for autopilot lag［J］.Aerospace Science and Technology，2013，25(1):132-137.

［8］曲萍萍，周荻.考慮導彈自動駕駛儀二階動態特性的三維導引律［J］.航空學報，2011，32(11):2096-2105.QU Pingping，ZHOU Di.Three-dimensional guidance law accounting for second-order dynamics of missile autopilot［J］.Acta Aeronautica et Astronautica Sinica，2011，32(11):2096-2105.(in Chinese)

［9］Qu P P，Zhou D.Observer-based guidance law accounting for second-order dynamics of missile autopilots［J］.Journal of Harbin Institute of Technology，2013，20(1):17-22.

［10］Yeom J H，Hong J W，Yoo S J.Terminal-phase optimal guidance law for BTT missiles considering significant autopilot dynamics［C］//Proceedings of AIAA Guidance，Navigation，and Control Conference，Portland，Oregon，2011.

［11］鄭立偉，荊武興，谷立祥.一種適用于大氣層外動能攔截器的末制導律［J］.航空學報，2007，28(4):953-958.ZHENG Liwei，JING Wuxing，GU Lixiang.A terminal guidance law for exoatmospheric kill vehicle［J］.Acta Aeronautica et Astronautica Sinica，2007，28(4):953-958.(in Chinese)

［12］陳峰，肖業倫，陳萬春.基于零控脫靶量的大氣層外超遠程攔截制導［J］.航空學報，2009，30(9):1583-1589.CHEN Feng，XIAO Yelun，CHEN Wanchun.Guidance based on zero effort miss for super-range exoatmospheric intercept［J］.Acta Aeronautica et Astronautica Sinica，2009，30(9):1583-1589.(in Chinese)

［13］李運遷.大氣層內攔截彈制導控制及一體化研究［D］.哈爾濱:哈爾濱工業大學，2011.LI Yunqian.Integrated guidance and control for endoatmospheric interceptors［D］.Harbin:Harbin Institute of Technology，2011.(in Chinese)

［14］丁世宏，李世華.有限時間控制問題綜述［J］.控制與決策，2011，26(2):161-169.DING Shihong，LI Shihua.A survey for finite-time control problems［J］.Control and Decision，2011，26(2):161-169.(in Chinese)