融合量子理論的結(jié)構(gòu)元素尺寸自適應調(diào)整策略*

張培林， 陳彥龍， 李 兵， 吳定海

(1.軍械工程學院七系 石家莊，050003) (2.軍械工程學院四系 石家莊，050003)

?

融合量子理論的結(jié)構(gòu)元素尺寸自適應調(diào)整策略*

張培林1， 陳彥龍1， 李 兵2， 吳定海1

(1.軍械工程學院七系 石家莊，050003) (2.軍械工程學院四系 石家莊，050003)

受量子理論啟發(fā)，提出一種針對數(shù)學形態(tài)學結(jié)構(gòu)元素尺寸自適應調(diào)整的新策略，以達到更優(yōu)的沖擊響應信號形態(tài)學提取效果。首先，結(jié)合量子理論建立起振動信號的量子系統(tǒng)，在此基礎(chǔ)上提出了振動信號的量子比特數(shù)學表達式，用于刻畫振動信號的狀態(tài)；然后，針對機械振動信號的局部特點，分析1×3鄰域的振動信號相關(guān)性，提出了機械振動信號在量子概率特征下的結(jié)構(gòu)元素尺寸衡量算子；最后，依據(jù)尺寸衡量算子和自適應控制結(jié)構(gòu)元素的長度達到更優(yōu)的濾波效果。利用該策略對軸承沖擊故障信號進行形態(tài)濾波，并與傳統(tǒng)方法進行了比較，結(jié)果表明該方法可以有效提取信號的全局和局部特征。

振動分析方法； 沖擊響應； 量子力學； 數(shù)學形態(tài)學； 結(jié)構(gòu)元素； 自適應

引 言

機械設(shè)備結(jié)構(gòu)復雜，為實現(xiàn)高效安全生產(chǎn)，需要對設(shè)備的運行狀態(tài)進行快速有效的評估。當機械設(shè)備發(fā)生故障時，運轉(zhuǎn)過程中會產(chǎn)生沖擊力，振動信號中將出現(xiàn)沖擊響應成分，監(jiān)測信號將發(fā)生突變。因此，準確地提取沖擊響應信號，快速地診斷故障，能夠顯著提高設(shè)備的監(jiān)測管理效率。

數(shù)學形態(tài)學具有良好的信號處理能力，研究表明[1-3]，不同的結(jié)構(gòu)元素(structuring element，簡稱SE)長度將對分析產(chǎn)生極大影響。然而，對于現(xiàn)場采集的故障信號，由于沖擊響應成分的先驗知識匱乏，難以選擇合適長度的SE；另一方面，信號在不同的時刻，局部特征存在差異，固定SE長度的細節(jié)處理能力欠缺，無法實現(xiàn)信號的最優(yōu)處理[4]。文獻[5]通過動態(tài)調(diào)整橢圓形結(jié)構(gòu)元素的長度，實現(xiàn)了圖像的邊緣連接。文獻[6]自適應地調(diào)整圓形結(jié)構(gòu)元素的長度，并應用于木質(zhì)識別。文獻[7]采用多尺度形態(tài)學分析，通過改變結(jié)構(gòu)元素的尺度，取得了良好的圖像分析效果。以上方法均針對圖像，為提高形態(tài)學處理一維機械信號的能力，需要針對一維振動信號的特征，對結(jié)構(gòu)元素的尺寸實現(xiàn)自適應調(diào)整。

量子理論對物理世界的描述方法，推動著其他領(lǐng)域的快速發(fā)展[8-10]，目前已在快速檢索、信號加密和圖像處理等領(lǐng)域取得了大量成果，顯示出量子理論的巨大研究價值。筆者受量子理論啟發(fā)，提出融合量子理論的結(jié)構(gòu)元素尺寸自適應調(diào)整策略(adaptive adjustment strategy of structuring element length integrating quantum theory，簡稱AASQT)，并應用于沖擊響應信號的提取。采用量子理論量化振動信號的局部特征，用于指導SE長度的選擇，最終實現(xiàn)SE尺寸的自適應調(diào)整，并利用具有自適應長度的結(jié)構(gòu)元素(adaptive length structuring element，簡稱ALSE)完成對故障沖擊響應信號的優(yōu)化提取。采用實測軸承內(nèi)圈故障信號進行測試，并與采用固定長度結(jié)構(gòu)元素(fix length structuring element，簡稱FLSE)的形態(tài)學處理結(jié)果進行對比，結(jié)果表明，采用AASQT的形態(tài)學處理方法能在強背景噪聲下有效提取出故障的沖擊響應成分，兼顧了信號的全局和局部特征，且計算快速，可應用于機械設(shè)備的在線監(jiān)測。

1 數(shù)學形態(tài)分析

1.1 形態(tài)學梯度算子

數(shù)學形態(tài)學變換對非線性振動信號具有極強的分析能力，它根據(jù)對象的幾何特征，利用SE對信號進行度量或修正，以達到提取有用信息的目的[6]。筆者采用形態(tài)梯度算子作為形態(tài)濾波器[11]

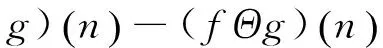
(1)

在一維信號分析中，由于形態(tài)梯度算子可以檢測暫態(tài)信息，因此成為凸顯沖擊響應信息的有力工具，研究發(fā)現(xiàn)它能夠在準確檢測出沖擊響應位置的同時，有效保留沖擊響應形狀。

1.2 結(jié)構(gòu)元素的參數(shù)設(shè)置

確定形態(tài)濾波器的形式后，結(jié)構(gòu)元素成為影響形態(tài)學處理效果的關(guān)鍵因素。由于扁平型結(jié)構(gòu)元素(SE的幅值為0)避免了對信號幅值的修改且運算量少，因此筆者采用平型結(jié)構(gòu)元素。

扁平結(jié)構(gòu)元素由于幅值為0，在形態(tài)運算中參數(shù)設(shè)置僅涉及到長度。研究表明[2,12]，采用不同的長度結(jié)構(gòu)元素，對信號的分析效果影響極大。文獻[12]以沖擊響應次數(shù)最多為準則得出0.6d～0.7d(d為沖擊響應周期內(nèi)采樣點數(shù))為最佳結(jié)構(gòu)元素長度，但當采樣頻率較大時，SE長度仍會在一個較大范圍內(nèi)浮動，元素的長度仍然難以確定。由于一個信號中包含較多的成分，使用FLSE分析時只能提取出與SE相匹配的成分，為實現(xiàn)更好的信號分析效果，需要SE的尺寸隨著信號的局部特征自適應變化。

結(jié)合量子理論，筆者對信號的局部特征進行定量分析，將分析結(jié)果作為SE尺寸自適應變化的依據(jù)，實現(xiàn)SE尺寸在0.6d～0.7d內(nèi)自適應變動。

2 振動信號的量子系統(tǒng)

量子比特的狀態(tài)是|0〉和|1〉兩種量子態(tài)的線性疊加，其數(shù)學形式為

|φ〉=a|0〉+b|1〉

(2)

其中：a，b為量子態(tài)的概率幅，為滿足歸一化條件|a|2+|b|2=1的復數(shù)，|a|2，|b|2分別為式中|0〉，|1〉兩個基態(tài)的出現(xiàn)概率。

式(2)表明，量子比特描述的狀態(tài)是不確定的，它能夠以不同的概率表示各種狀態(tài)。如果用|0〉代表振動信號的一種狀態(tài)，用|1〉代表振動信號的另一種狀態(tài)，分析概率幅a和b就能夠得出振動信號的不同狀態(tài)，有利于刻畫信號的局部特征。

若一個振動信號由k個量子位描述，其中第m個量子位的狀態(tài)為|φm>=am|0〉+bm|1〉，該振動信號的狀態(tài)可用k個單量子比特的直積態(tài)表示為

(3)

其中：|mb〉表示含k個量子比特的量子系統(tǒng)|φ〉(振動信號)的基態(tài)，為二進制表達形式，其意義為量子系統(tǒng)(振動信號)|φ〉的第m個基態(tài)；wm為相應基態(tài)的概率幅。

|wm|2表示基態(tài)|mb〉的出現(xiàn)概率，根據(jù)量子表達式的要求，需滿足式(4)的條件。

(4)

3 結(jié)構(gòu)元素自適應調(diào)整策略

3.1 振動信號的量子比特

振動信號的量子系統(tǒng)里最關(guān)鍵的部分是振動信號的量子比特，本部分將給出振動信號量子比特的數(shù)學表達式。

假設(shè)傳感器采集信號為s(i)(i=0，1，…，n-1)，對s(i)歸一化得到信號y(i)∈[0，1]。引入自適應閾值T∈(smin，smax)，采用的歸一化變換為

(5)

機械振動信號雖然包含非平穩(wěn)、非線性成分以及各類干擾噪聲，但在本質(zhì)上具有統(tǒng)計性[13-14]，從概率統(tǒng)計的角度出發(fā)處理信息的啟發(fā)[15-16]，提出式(6)所示的振動信號量子比特的數(shù)學表達式，用以實現(xiàn)振動信號從時域空間到量子空間的映射

(6)

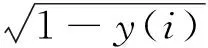
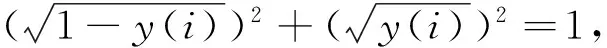
3.2 尺寸衡量算子

在振動信號量子比特的基礎(chǔ)上，結(jié)合振動信號的相關(guān)性，提出機械振動信號在量子概率特征下的結(jié)構(gòu)元素尺寸衡量算子(length measurement operator，簡稱LMO)，用于指導結(jié)構(gòu)元素尺寸的自適應選擇。

圖1為原始信號s(i)的1×3鄰域窗口，該鄰域窗口可構(gòu)成3量子位系統(tǒng)，其態(tài)矢為|s(i-1)s(i)s(i+1)〉。利用式(5)得到s(i)的歸一化數(shù)值y(i)∈[0，1]，結(jié)合式(3)可知，對于三量子比特系統(tǒng)，則該|s(i-1)s(i)s(i+1)〉可表示為

(7)

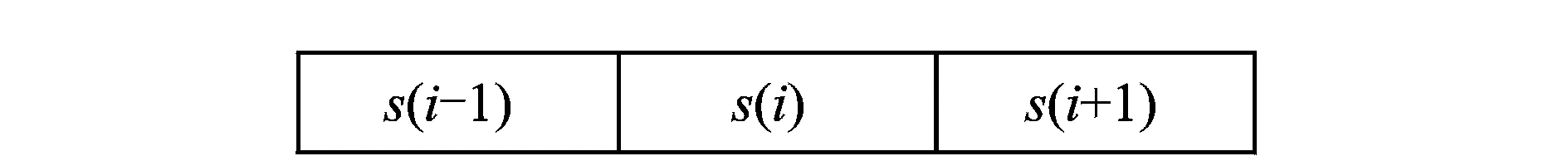
圖1 1×3鄰域位置關(guān)系
Fig.1 1×3 neighborhood

機械設(shè)備的振動具有較強的關(guān)聯(lián)性，相鄰時刻的振動大小關(guān)聯(lián)緊密，而噪聲不具備此特點，基于此在1×3窗口中提出尺寸衡量算子。從三量子位系統(tǒng)基態(tài)概率統(tǒng)計的角度出發(fā)，LMO在1×3窗口中沿水平方向進行處理，運用LMO輸出的數(shù)值作為對應位置的SE長度的衡量指標。

LMO用于選擇最佳的結(jié)構(gòu)元素尺寸，提取故障的沖擊響應信號，在數(shù)值處理上需要符合沖擊響應信號的特征。因此，一方面LMO統(tǒng)計峰值信息，對應振動基態(tài)為|010〉；另一方面，保留振動信號的波谷信息，對應振動基態(tài)為|101〉。結(jié)合式(3)，波峰波谷信息對應的十進制為2，5。所以，LMO取m=2，5時兩種基態(tài)的概率總和。LMO的表達式為

siz(i)=sum{|wm|2,m=2,5}

(8)

其中：siz指LMO定量衡量的結(jié)果，siz可進一步表示為

(9)

式(9)給出了LMO的計算方法。從算子的計算過程來看，水平方向上，從左到右和從右到左，該算子都能得到相同的結(jié)果，表明了該算子具備較強的適應能力。

對于長度為n的振動信號，LMO的時間復雜度為O(n)，該方法能夠快速地完成計算。

3.3 結(jié)構(gòu)元素的長度

機械振動信號在量子概率特征下的SE尺寸衡量算子siz描述了振動信號中沖擊響應信號局部特征，以此為依據(jù)可以有效地進行SE的尺寸選擇。根據(jù)文獻[12]的曲線圖，確定結(jié)構(gòu)元素的自適應尺寸為

(10)

其中：len指根據(jù)文獻[12]擬合的結(jié)構(gòu)元素長度變化曲線，即

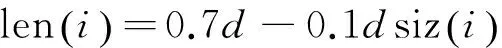
(11)

式(10，11)能夠保證結(jié)構(gòu)元素的尺寸在0.6d～0.7d范圍內(nèi)變動，實現(xiàn)SE長度的自適應調(diào)整，依據(jù)此方法獲得的結(jié)構(gòu)元素稱為自適應長度結(jié)構(gòu)元素(ALSE)。

3.4 閾值處理

在1×3振動信號窗口中，LMO能夠有效描述振動信號的沖擊響應細節(jié)特征。在量子概率LMO中，通過參數(shù)T可有效調(diào)節(jié)振動信號的細節(jié)部分，為了保證機械振動信號處理效果，需對閾值參數(shù)T的設(shè)定進行處理，筆者以形態(tài)濾波后的振動信號信息熵最大化為原則，自適應確定閾值參數(shù)T。兼顧計算成本和算法效果，在確定T的過程中，T的迭代步長為0.01。

根據(jù)信息論，經(jīng)ALSE形態(tài)濾波后所得振動信號ssiz(i)的信息熵公式為

H(ssiz)=-∑p(x)lgp(x)

(12)

其中：p(x)表示經(jīng)ALSE形態(tài)濾波后的振動信號ssiz(i)中，振動大小為x的出現(xiàn)概率。

3.5 采用AASQT的形態(tài)濾波器

采用AASQT的形態(tài)濾波器步驟描述如下：

1) 讀入機械振動信號s(i)；

2) 初始化參數(shù)T=smin+0.01，變量opt_h=0，opt_T=0，opt_h和opt_T分別用于存放當前最大信息熵及其對應的閾值T；

3) 將閾值參數(shù)T代入式(5)歸一化振動信號得到y(tǒng)(i)；

4) 在當前T取值情況下，根據(jù)式(9)獲得LMO的輸出值；

5) 根據(jù)LMO的輸出，利用式(10，11)獲得各個采樣點的扁平SE自適應尺寸；

6) 根據(jù)式(1)，利用各個采樣點對應長度的SE進行濾波，得到振動信號ssiz(i)；

7) 根據(jù)式(12)計算ssiz(i)信息熵H；

8) 若信息熵H〉opt_h，則更新opt_h，opt_T；否則opt_h，opt_T保持不變；

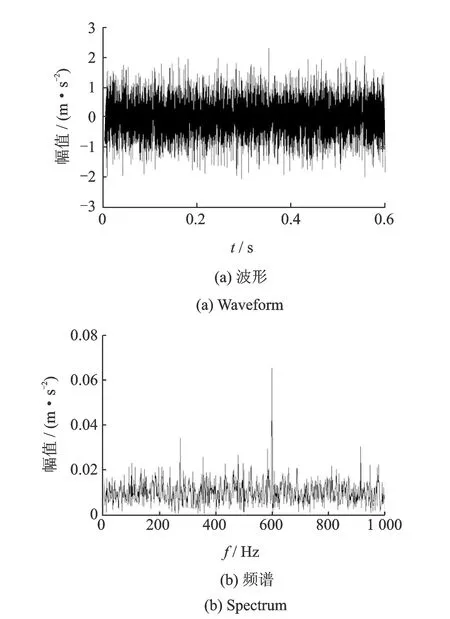
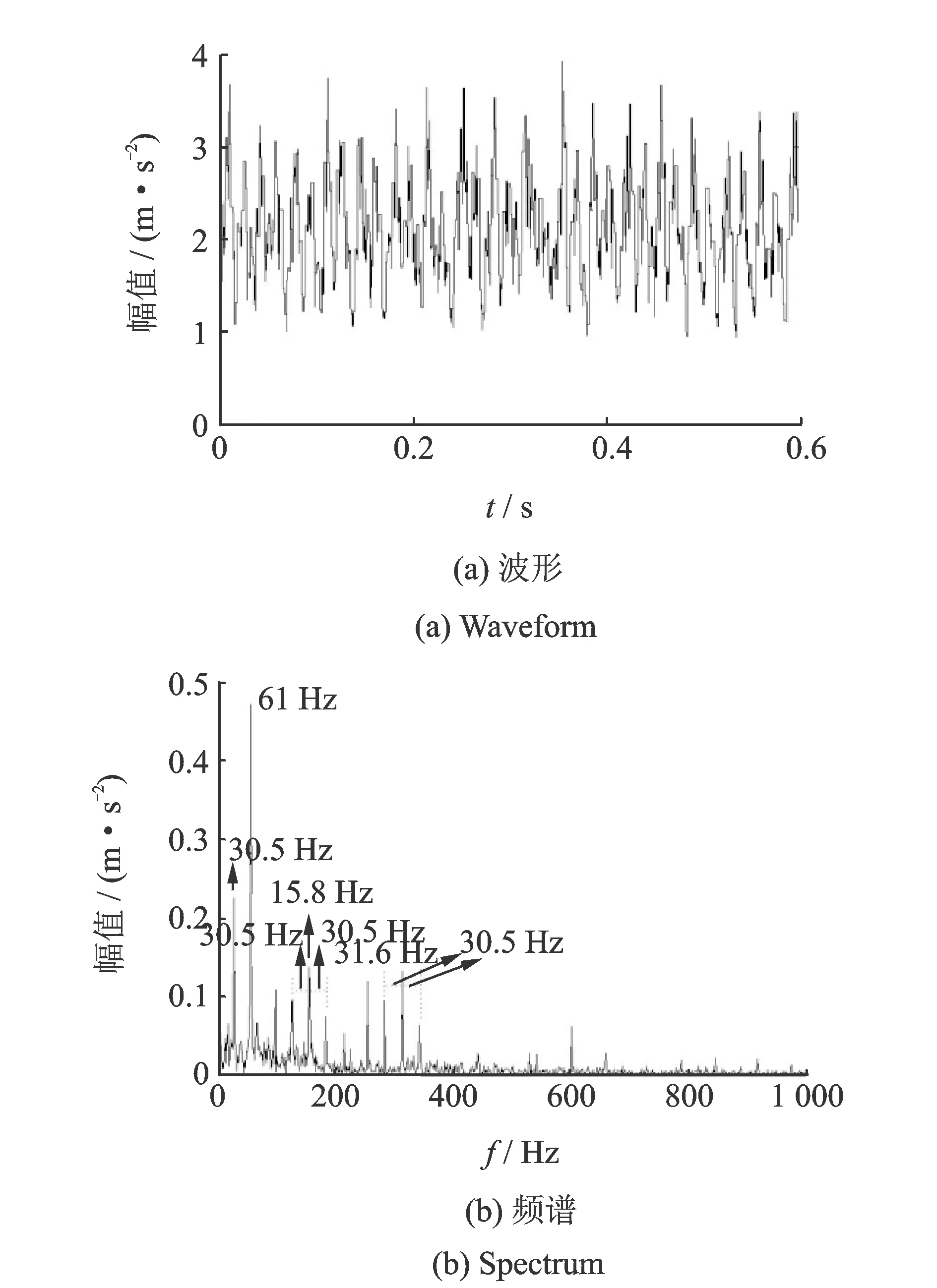
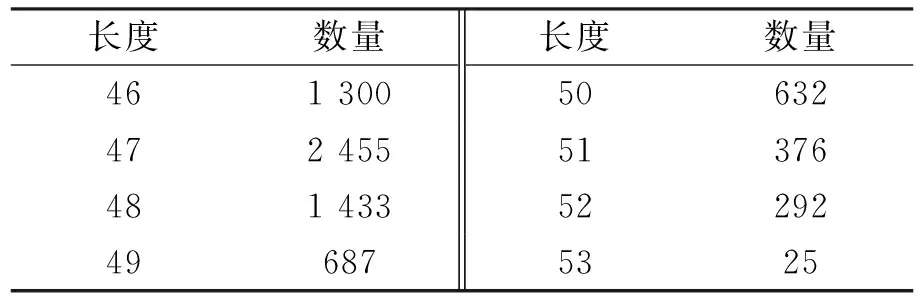
9) 執(zhí)行T=T+0.01，如果T

10) 令T=opt_T，重復步驟3)～6)，得到最終的輸出信號ssiz(i)。

4 實驗結(jié)果與分析

采用某機械裝備的綜合傳動裝置進行研究。在軸承內(nèi)圈上加工出3 mm×0.2 mm(長×深)的劃痕用于模擬沖擊故障，使振動信號中包含沖擊響應成分。采集加速度振動信號，實測轉(zhuǎn)動速度為1 830 r/min(30.5 Hz)，在3檔檔位上測量，傳感器安裝在對應軸承位置的箱蓋上方。內(nèi)圈故障理論頻率應為158 Hz。

采樣頻率為12 kHz，采樣時間為0.6 s，故障信號波形如圖2所示。頻譜中可以看出，故障頻率淹沒在噪聲頻率中。

圖2 含強噪聲故障信號Fig.2 Fault signal with strong noise

圖3 固定長度結(jié)構(gòu)元素處理結(jié)果Fig.3 Result of FLSE

采用固定長度結(jié)構(gòu)元素進行形態(tài)梯度算子濾波，SE為扁平型，根據(jù)文獻[12]設(shè)定SE長度為46，處理結(jié)果圖3所示。采用FLSE能夠在強背景噪聲下提取出一部分沖擊響應信息，從圖3(b)能夠看出，F(xiàn)LSE提取出的信號存在較多無關(guān)頻率，特征頻率158 Hz周圍存在較強的干擾，158 Hz及其二倍頻316 Hz的邊帶也難以觀察，不利于故障的診斷。

采用筆者提出的方法AASQT進行濾波處理，圖4為獲得的波形和頻譜，有效地提取出故障沖擊響應信號。故障特征頻率158 Hz、二倍頻316 Hz明顯，且158 Hz和316 Hz存在明顯的邊帶，間隔30.5 Hz與轉(zhuǎn)頻的大小一致；同時，轉(zhuǎn)頻30.5 Hz及其二倍頻61 Hz明顯。以上特征與軸承內(nèi)圈故障的特點吻合，可以判定軸承的內(nèi)圈發(fā)生故障。

圖4 自適應調(diào)整策略處理結(jié)果Fig.4 Result of AASQT

圖5 結(jié)構(gòu)元素長度變化Fig.5 Length change in SE

圖5為采用AASQT進行形態(tài)學處理時，不同采樣點位置的SE長度，為便于觀察，只顯示前200個采樣點對應的SE長度，可以看出在不同的采樣點位置，SE長度不同，SE長度能夠根據(jù)信號的局部特征自適應調(diào)整。表1為信號處理過程中SE的長度統(tǒng)計，0.6 s中共計包含7 200個采樣點。由于故障頻率為158 Hz，采樣頻率為12 kHz，因此沖擊響應周期內(nèi)采樣點數(shù)為76，0.6d～0.7d對應SE長度范圍為46～53。由表1可見，SE長度主要分布在46～48，最大長度為53，最小長度為46。筆者所提方法AASQT根據(jù)信號的局部特征，能夠更恰當?shù)姆峙銼E長度，最終將獲得更好的全局效果，因此本研究方法從本質(zhì)上說兼顧了信號的局部和全局特征。

為更加客觀地評價采用AASQT進行形態(tài)濾波的沖擊響應信號提取能力，運用特征頻率強度系數(shù)對處理后的信號進行定量評價，特征頻率強度系數(shù)Cf定義[2]為

表1 結(jié)構(gòu)元素長度統(tǒng)計

(13)

其中：Fj代表頻譜中的各頻率的大小；FCi為特征頻率的大小，這里取N=2；Cf表示特征頻率在整個頻譜圖中所占的能量，Cf越大，表明特征頻率越容易觀察。

表2比較了采用FLSE和ALSE獲得的Cf，采用AASQT效果最佳。

表2 特征頻率強度系數(shù)比較

5 結(jié)束語

結(jié)合量子理論，筆者提出一種全新的結(jié)構(gòu)元素尺寸自適應調(diào)整方法，并用于沖擊響應信號的提取。主要工作包括：構(gòu)建振動信號的量子系統(tǒng)；建立振動信號的量子比特表達式；采用量子統(tǒng)計概率量化振動信號的局部特征，并以此為依據(jù)對結(jié)構(gòu)元素的長度進行了優(yōu)化選擇，實現(xiàn)了形態(tài)學結(jié)構(gòu)元素的長度自適應調(diào)整。實驗研究表明，所提方法綜合考慮了振動信號的全局和局部特征，采用該策略的形態(tài)濾波器對機械故障沖擊信號具有較好的提取能力且計算速度快，為強背景噪聲下的機械故障信息提取提供了一條新途徑。

[1] Zafeiriou S, Petrou M. 2.5D Elastic graph matching[J]. Computer Vision and Image Understanding, 2011, 115(7): 1062-1072.

[2] Li Bing, Zhang Peilin, Wang Zhengjun, et al. A weighted multi-scale morphological gradient filter for rolling element bearing fault detection[J]. ISA Transactions, 2011, 50(4): 599-608.

[3] Li Qiyue, Xu Jie, Wang Weihua, et al. Slope displacement prediction based on morphological filtering[J]. Journal of Central South University, 2013, 20(6): 1724-1730.

[4] Hao Rujiang, Peng Zhiyong, Feng Zhipeng, et al. Application of support vector machine based on pattern spectrum entropy in fault diagnostics of rolling element bearings[J]. Measurement Science and Technology, 2011, 22 (10): 1-13.

[5] Frank Y, Cheng S X. Adaptive mathematical morphology for edge linking[J]. Information Sciences, 2004, 167(1): 9-12.

[6] Shen P, Mineichi K. Segmentation of pores in wood microscopic images based on mathematical morphology with a variable structuring element[J]. Computers and Electronics in Agriculture, 2011, 75(2): 250-260.

[7] Bai Xiangzhi, Zhou Fusheng, Xue Bindang. Infrared image enhancement through contrast enhancement by using multiscale new top-hat transform[J]. Infrared Physics & Technology, 2011, 54(7): 61-69.

[8] Lu T C, Yu G R. An adaptive population multiobjective quantum inspired evolutionary algorithm for multiobjective 0/1 knapsack problems[J]. Information Sciences, 2013, 243(9): 39-56.

[9] Niu Qun, Zhou Taijin, Fei Minrui, et al. An efficient quantum immune algorithm to minimize mean flow time for hybrid flow shop problems[J]. Mathematics and Computers in Simulation, 2012, 84(10): 1-25.

[10]Li Yangyang, Shi Hongzhu, Jiao Licheng, et al. Quantum evolutionary clustering algorithm based on watershed applied to SAR images egmentation[J]. Neurocomputing, 2012, 87(6): 90-98.

[11]李兵, 張培林, 劉東升, 等. 基于形態(tài)梯度解調(diào)算子的齒輪故障特征提取[J]. 振動、測試與診斷, 2010, 30 (1): 39-42.

Li Bing, Zhang Peilin, Liu Dongsheng, et al. Feature extraction for gear fault diagnosis using morphological gradient demodulation[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1): 39-42.(in Chinese)

[12]Nikolaou N G, Antoniadis I A. Application of morphological operators as envelope extractors for impulsive-type periodic signals[J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1147-1162.

[13]Dwivedi U D, Singh S N. Enhanced detection of power-quality events using intra and interscale dependencies of wavelet coefficients[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 358-366.

[14]林勇, 胡夏夏, 朱根興, 等. 基于振動譜圖像識別的智能故障診斷[J]. 振動、測試與診斷, 2010, 30 (2): 175-180.

Lin Yong , Hu Xiaxia, Zhu Genxing, et al. Intelligent fault diagnosis using image recognition of vibration spectrogram[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 175-180. (in Chinese)

[15]Fu Xiaowei, Ding Mingyue, Cai Chao. Despeckling of medical ultrasound images based on quantum-inspired adaptive threshold[J]. Electronics Letters, 2010, 46(13): 52-53.

[16]謝可夫, 羅安. 量子啟發(fā)數(shù)學形態(tài)學的研究[J]. 電子學報, 2006, 33 (2): 284-287.

Xie Kefu, Luo An. Research on quantum-inspired mathematical morphology[J]. Acta Electronica Sinica, 2006, 33(2): 284-287. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.008

*國家自然科學基金資助項目(51205405，51305454)

2013-08-28；

2013-10-15

TH113.1; TN911.7

張培林，男，1955年12月生，教授、博士生導師。主要研究方向為地面運載平臺維修理論與技術(shù)。曾發(fā)表《自適應Laplace統(tǒng)計模型下的量子降噪算法》(《振動、測試與診斷》2014年第34卷第5期)等論文。

E-mail：chenyanlong110@163.com