基于小波分析的簡(jiǎn)支梁橋損傷識(shí)別*

劉習(xí)軍， 相林杰， 張素俠

(1. 天津大學(xué)機(jī)械工程學(xué)院 天津， 300072)(2. 天津市非線性動(dòng)力學(xué)與混沌控制重點(diǎn)實(shí)驗(yàn)室 天津, 300072)

?

基于小波分析的簡(jiǎn)支梁橋損傷識(shí)別*

劉習(xí)軍1,2， 相林杰1,2， 張素俠1,2

(1. 天津大學(xué)機(jī)械工程學(xué)院 天津， 300072)(2. 天津市非線性動(dòng)力學(xué)與混沌控制重點(diǎn)實(shí)驗(yàn)室 天津, 300072)

提出了基于小波子帶信號(hào)能量曲率變化的損傷識(shí)別方法。分別對(duì)完好和損傷狀態(tài)下結(jié)構(gòu)的振動(dòng)響應(yīng)進(jìn)行二進(jìn)離散小波變換，通過(guò)信號(hào)子帶分解與重構(gòu)將響應(yīng)分解到不同頻帶，使疊加的模態(tài)響應(yīng)分離。定義了信號(hào)相對(duì)能量曲率差損傷指標(biāo)，利用該指標(biāo)對(duì)結(jié)構(gòu)的損傷進(jìn)行識(shí)別定位。應(yīng)用此方法對(duì)一簡(jiǎn)支梁橋進(jìn)行損傷數(shù)值分析，結(jié)果表明：二進(jìn)離散小波變換可以對(duì)結(jié)構(gòu)振動(dòng)響應(yīng)中疊加的多階模態(tài)信息進(jìn)行有效分離；信號(hào)相對(duì)能量曲率差指標(biāo)可以對(duì)損傷進(jìn)行有效識(shí)別，且不受激勵(lì)位置及荷載大小影響。最后通過(guò)模型實(shí)驗(yàn)驗(yàn)證了該方法的正確性及可行性。

簡(jiǎn)支梁橋; 損傷識(shí)別; 小波變換; 能量曲率

引 言

橋梁結(jié)構(gòu)損傷識(shí)別是進(jìn)行橋梁承載力評(píng)估以及制定維修、養(yǎng)護(hù)策略的重要前提。近年來(lái)，隨著小波分析理論的發(fā)展及其在機(jī)械、航空等領(lǐng)域的應(yīng)用，基于小波分析的橋梁結(jié)構(gòu)損傷識(shí)別方法得到了廣泛的研究。目前，國(guó)內(nèi)外相關(guān)研究的主要內(nèi)容有：a.將結(jié)構(gòu)位移模態(tài)、曲率模態(tài)等與小波變換相結(jié)合的損傷識(shí)別方法[1-3]； b.將小波變換與信息熵、神經(jīng)網(wǎng)絡(luò)等方法相結(jié)合的損傷識(shí)別方法[4-6]； c.將結(jié)構(gòu)響應(yīng)進(jìn)行小波包分解，利用分解后各頻段能量變化構(gòu)造損傷指標(biāo)。大量研究結(jié)果表明，小波包能量的變化對(duì)損傷非常敏感[7-11]。

通過(guò)分析結(jié)構(gòu)在沖擊激勵(lì)下振動(dòng)響應(yīng)頻率成分及二進(jìn)小波分解頻帶劃分規(guī)律，筆者采用二進(jìn)離散小波變換對(duì)結(jié)構(gòu)振動(dòng)響應(yīng)進(jìn)行子帶分解與重構(gòu)，定義信號(hào)相對(duì)能量曲率差損傷指標(biāo)，并對(duì)損傷進(jìn)行識(shí)別定位。通過(guò)數(shù)值算例及模型實(shí)驗(yàn)對(duì)該損傷識(shí)別方法的正確性和可行性進(jìn)行了驗(yàn)證。

1 基于小波分析的損傷識(shí)別理論及過(guò)程

1.1 小波分析理論簡(jiǎn)介

小波分析是在傅里葉變換的基礎(chǔ)上發(fā)展起來(lái)的

信號(hào)處理手段，在時(shí)頻兩域都具有表征信號(hào)局部特征的能力[12]。以3層分解為例，利用小波分析進(jìn)行信號(hào)分解的樹(shù)形結(jié)構(gòu)及各子帶信號(hào)頻帶范圍如圖1所示。

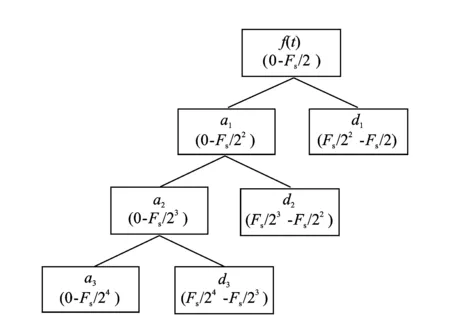
圖1 信號(hào)的3層小波分解及頻帶劃分規(guī)律Fig.1 Wavelet decomposition and its frequency band partition theory

圖1中，F(xiàn)s為原始信號(hào)的采樣頻率。可見(jiàn)利用小波對(duì)信號(hào)進(jìn)行分解，是將信號(hào)分解成低頻和高頻各占一半帶寬的頻帶，但每次分解均只對(duì)低頻部分進(jìn)行更深層次的分解，因此小波分解高頻部分分辨率較差。各子帶信號(hào)與原始信號(hào)具有如下關(guān)系

f(t)=an+dn+dn-1+…+d2+d1

(1)

其中：f(t)為原信號(hào)；a為低頻近似部分；d為高頻細(xì)節(jié)部分；n代表分解層次。

通過(guò)以上分析可知，對(duì)于一個(gè)給定的信號(hào)可以確定合適的分解層次，使所關(guān)心的頻率成分落入某一頻帶，從而進(jìn)行提取作進(jìn)一步分析。

1.2 小波分析的結(jié)構(gòu)損傷識(shí)別過(guò)程

1.2.1 小波分解的相對(duì)能量向量的構(gòu)造

結(jié)構(gòu)在瞬態(tài)沖擊激勵(lì)下，其振動(dòng)響應(yīng)為多個(gè)模態(tài)響應(yīng)的疊加。應(yīng)用小波對(duì)響應(yīng)信號(hào)進(jìn)行分解。在分解過(guò)程中，若出現(xiàn)某頻率接近對(duì)半分解的中間區(qū)域，此時(shí)可改變采樣頻率或分解層次，重新劃分頻帶，使響應(yīng)中所包含的各階信號(hào)成分分解到不同頻帶。假設(shè)在結(jié)構(gòu)上布設(shè)的傳感器數(shù)目為n，則各個(gè)測(cè)點(diǎn)的響應(yīng)信號(hào)經(jīng)過(guò)小波分解之后可得到信號(hào)向量X為

(2)

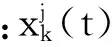
向量X包含了結(jié)構(gòu)各個(gè)測(cè)點(diǎn)以第k階固有振型振動(dòng)的信息。

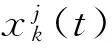
(3)

其中：T為信號(hào)采樣時(shí)間。

于是可得到信號(hào)能量向量E為

(4)

將各測(cè)點(diǎn)同階振動(dòng)信號(hào)能量關(guān)于所有測(cè)點(diǎn)該階振動(dòng)信號(hào)能量總和歸一化，得

(5)

得到信號(hào)相對(duì)能量向量e為

(6)

信號(hào)相對(duì)能量向量e反映了結(jié)構(gòu)各測(cè)點(diǎn)以某階振型振動(dòng)時(shí)的相對(duì)強(qiáng)弱狀態(tài)。通過(guò)式(5)的歸一化處理，消除了激振力大小的影響，即結(jié)構(gòu)損傷前后激勵(lì)大小不必保持一致，只需保持荷載形式相同即可。

1.2.2 相對(duì)能量曲率差的計(jì)算

通過(guò)計(jì)算分析發(fā)現(xiàn)，由某一階振動(dòng)信號(hào)計(jì)算得到的相對(duì)能量向量與同階振型向量分布有相似的特點(diǎn)，即結(jié)構(gòu)損傷前后相對(duì)能量在損傷位置具有局部奇異性。由差分法得

(7)

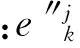
由此得到相對(duì)能量曲率向量e″為

(8)

相對(duì)能量曲率差Δe″為

Δe″=e″dk-e″uk

(9)

其中：e″dk，e″uk分別為結(jié)構(gòu)損傷狀態(tài)與完好狀態(tài)第k階振動(dòng)信號(hào)的相對(duì)能量曲率。

信號(hào)相對(duì)能量曲率差即為筆者進(jìn)行結(jié)構(gòu)損傷識(shí)別的指標(biāo)。當(dāng)結(jié)構(gòu)存在損傷時(shí)，結(jié)構(gòu)上各點(diǎn)信號(hào)相對(duì)能量曲率均發(fā)生變化，但在損傷位置變化最大，因此可根據(jù)相對(duì)能量曲率差變化最大值識(shí)別結(jié)構(gòu)損傷位置。

2 數(shù)值分析

以圖2所示的簡(jiǎn)支梁為例，梁長(zhǎng)為0.7 m，寬為0.17 m，厚為0.006 m，材料彈性模量為5 GPa，密度為1 210 kg/m3。單元?jiǎng)澐旨肮?jié)點(diǎn)編號(hào)如圖2所示。激振點(diǎn)位于8號(hào)點(diǎn)位置，距離左支座0.28 m。損傷的模擬采用主梁對(duì)稱切口，切口寬為0.002 m，深為0.02 m，設(shè)定兩種損傷狀態(tài)，分別為測(cè)點(diǎn)4和測(cè)點(diǎn)10對(duì)應(yīng)位置的梁體分別發(fā)生損傷。沖擊激勵(lì)的模擬如圖3所示，采樣頻率為500 Hz，采樣時(shí)長(zhǎng)為2.048 s。采用有限元程序進(jìn)行瞬態(tài)分析提取橋面板中線上19個(gè)節(jié)點(diǎn)的加速度響應(yīng)。

圖2 簡(jiǎn)支梁示意圖(單位:cm)Fig.2 Diagram of the simply supported beam (unit: cm)

圖3 荷載形式Fig.3 Load form

2.1 結(jié)構(gòu)完好狀態(tài)下各階振動(dòng)信號(hào)相對(duì)能量分布特征

結(jié)構(gòu)在完好狀態(tài)下，激振力大小分別取50, 70和100 N，計(jì)算各節(jié)點(diǎn)處的振動(dòng)加速度響應(yīng)。圖4(a), (b)分別為結(jié)構(gòu)在100 N激勵(lì)下4號(hào)點(diǎn)的加速度時(shí)程曲線及頻譜圖。可見(jiàn)，該點(diǎn)的振動(dòng)響應(yīng)為前幾階模態(tài)響應(yīng)的疊加。

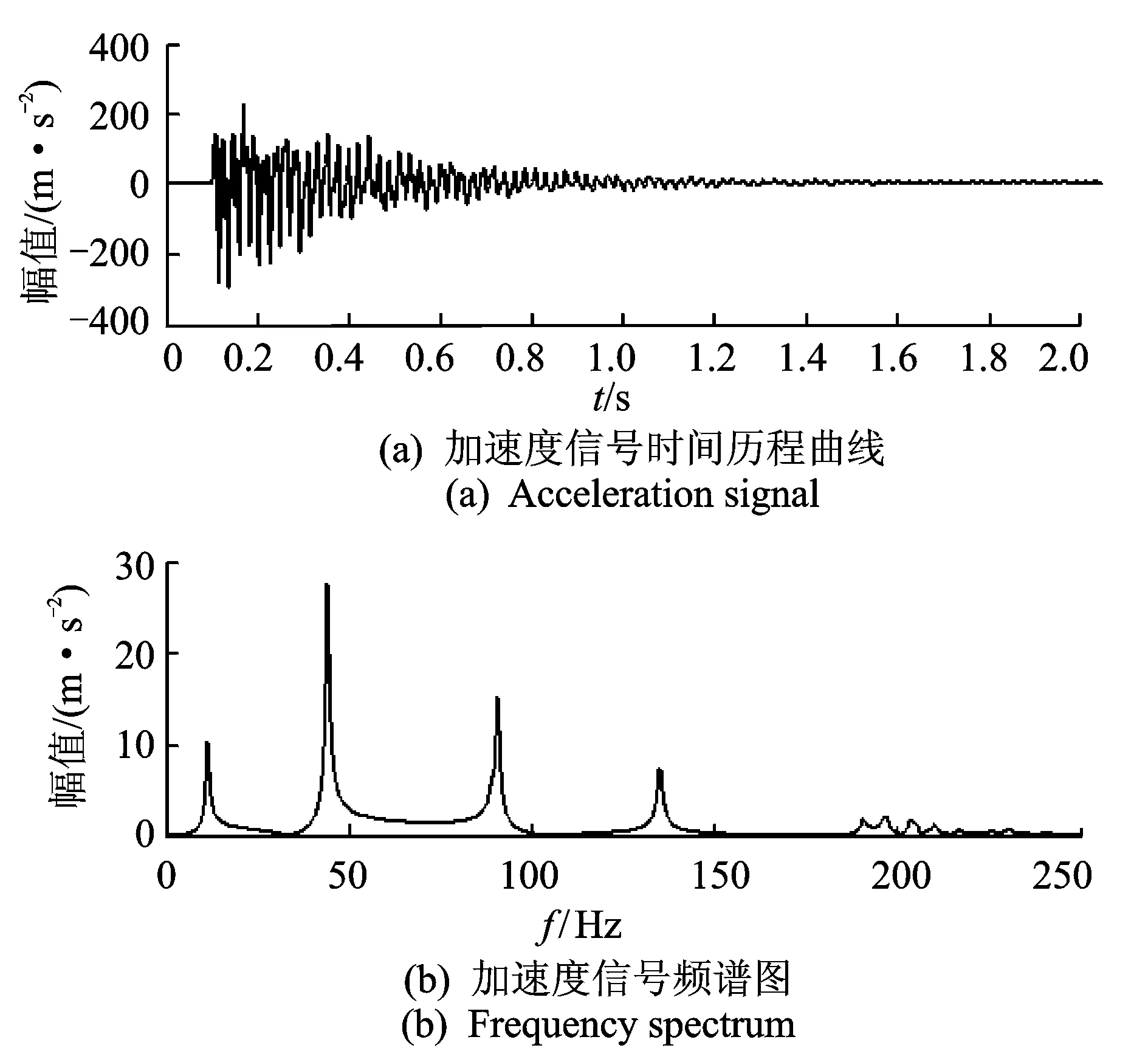
圖4 結(jié)構(gòu)完好狀態(tài)4號(hào)點(diǎn)加速度信號(hào)時(shí)間歷程及其頻譜圖Fig.4 Acceleration and frequency spectrum of point 4 under the intact condition

采用db4小波對(duì)該信號(hào)進(jìn)行3層小波分解并重構(gòu)，各子帶重構(gòu)信號(hào)及頻譜分析結(jié)果如圖5所示，得到a3,d3,d2和d1,共4個(gè)頻帶信號(hào)成分。其中a3,d3和d2部分均對(duì)應(yīng)結(jié)構(gòu)某一階固有頻率；d1部分則為4階及噪音成分。

對(duì)各點(diǎn)信號(hào)均作上述小波子帶分解與重構(gòu)，依次選取a3，d3和d2部分信號(hào)代入式(5)和式(6)計(jì)算信號(hào)相對(duì)能量。表1為完好結(jié)構(gòu)在激振力大小不同時(shí)a3部分的振動(dòng)信號(hào)各點(diǎn)相對(duì)能量分布。由表1可知，信號(hào)各點(diǎn)的相對(duì)能量分布與荷載大小無(wú)關(guān)。圖6(a～c)分別為a3，d3和d23個(gè)頻帶振動(dòng)信號(hào)沿各點(diǎn)的相對(duì)能量分布。可見(jiàn)，3個(gè)頻帶的振動(dòng)信號(hào)沿節(jié)點(diǎn)的相對(duì)能量分布同前3階固有振型有相似之處。a3部分振動(dòng)信號(hào)各點(diǎn)相對(duì)能量由跨中向兩側(cè)遞減，d3部分振動(dòng)信號(hào)相對(duì)能量在跨中位置出現(xiàn)零點(diǎn)，對(duì)應(yīng)第2階固有振型的節(jié)點(diǎn)，而d2部分振動(dòng)信號(hào)在點(diǎn)7和點(diǎn)13附近均接近零點(diǎn)，對(duì)應(yīng)3階振型的兩個(gè)節(jié)點(diǎn)。可以發(fā)現(xiàn)，采用筆者的分解方式可使疊加在響應(yīng)中的前幾階模態(tài)響應(yīng)有效分離，而分離出的“純模態(tài)”[14]其振動(dòng)信號(hào)相對(duì)能量分布同結(jié)構(gòu)振型一樣能夠反映結(jié)構(gòu)的固有特性，且對(duì)結(jié)構(gòu)局部變化較為敏感，由其變化可以反映結(jié)構(gòu)局部特性的變化。

圖5 各子帶重構(gòu)信號(hào)及其頻譜圖Fig.5 Sub-band signals and frequency spectrums under the intact condition

荷載測(cè) 點(diǎn) 編 號(hào)1234567891011121314151617181950N0.240.932.003.354.856.367.738.849.619.949.799.178.136.775.213.632.181.010.2670N0.240.932.003.354.856.367.738.849.619.949.799.178.136.775.213.632.181.010.26100N0.240.932.003.354.856.367.738.849.619.949.799.178.136.775.213.632.181.010.26

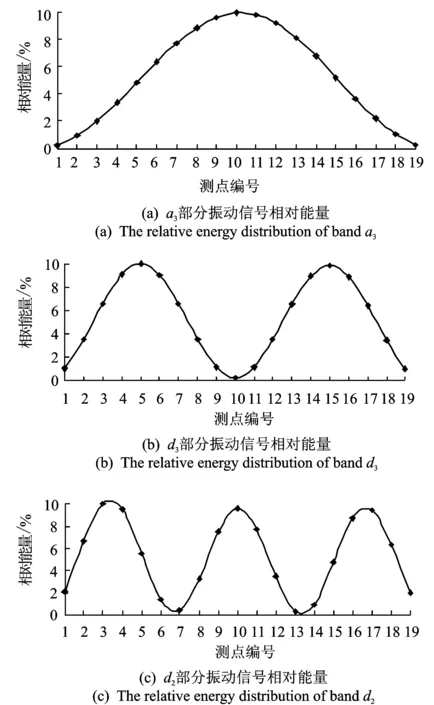
圖6 各子帶振動(dòng)信號(hào)相對(duì)能量分布Fig.6 The relative energy distribution of different sub-band signals

2.2 基于振動(dòng)信號(hào)相對(duì)能量曲率差的損傷識(shí)別

對(duì)結(jié)構(gòu)完好狀態(tài)與損傷狀態(tài)下各階振動(dòng)信號(hào)的相對(duì)能量分布向量由式(8)計(jì)算相對(duì)能量曲率并按式(9)計(jì)算曲率差。圖7為結(jié)構(gòu)在4號(hào)點(diǎn)處發(fā)生損傷時(shí)相對(duì)能量曲率差計(jì)算結(jié)果。由圖7可見(jiàn)，損傷使所有點(diǎn)的相對(duì)能量曲率差均發(fā)生了變化，但各階振動(dòng)信號(hào)均是在4號(hào)點(diǎn)損傷位置變化最大，即由變化最大值處可以識(shí)別損傷位置。從識(shí)別效果來(lái)看，由1, 2階振動(dòng)信號(hào)相對(duì)能量曲率差識(shí)別效果較好，3階振動(dòng)信號(hào)識(shí)別效果較差。

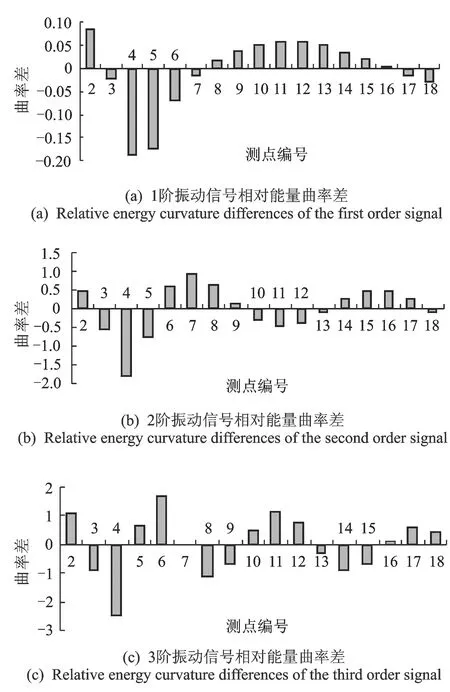
圖7 4號(hào)點(diǎn)處發(fā)生損傷時(shí)各階振動(dòng)信號(hào)相對(duì)能量曲率差Fig.7 Damage position-point 4: the relative energy curvature differences of different band signals

圖8為結(jié)構(gòu)在10號(hào)點(diǎn)(跨中)發(fā)生損傷時(shí)信號(hào)相對(duì)能量曲率差計(jì)算結(jié)果。可見(jiàn)，1， 3階振動(dòng)信號(hào)相對(duì)能量曲率差指標(biāo)均能很好地指示出損傷位置，而2階振動(dòng)信號(hào)未能正確指示出損傷位置，原因在于損傷位于跨中位置，對(duì)應(yīng)結(jié)構(gòu)豎向2階振型的節(jié)點(diǎn)，無(wú)論損傷與否，該位置振動(dòng)響應(yīng)中2階振動(dòng)信號(hào)能量均為零。

由以上結(jié)果不難理解當(dāng)結(jié)構(gòu)損傷位于某階振型節(jié)點(diǎn)時(shí)，通過(guò)該階振動(dòng)信號(hào)進(jìn)行損傷識(shí)別失效。同樣，當(dāng)激振點(diǎn)位于某階振型節(jié)點(diǎn)時(shí)，由于不能激出該階模態(tài)響應(yīng)，該階振動(dòng)信號(hào)亦不能正確識(shí)別損傷。

圖8 10號(hào)點(diǎn)處發(fā)生損傷時(shí)各階振動(dòng)信號(hào)相對(duì)能量曲率差Fig.8 Damage position-point 10: the relative energy curvature differences of different band signals

綜合以上分析，在實(shí)際應(yīng)用中建議選取第一階振動(dòng)信號(hào)構(gòu)造指標(biāo)進(jìn)行損傷識(shí)別。

在以曲率模態(tài)為基礎(chǔ)的損傷識(shí)別中，測(cè)點(diǎn)布置稀疏往往會(huì)造成計(jì)算結(jié)果具有較大誤差，重則造成指標(biāo)失效[15]。為考察文中提出的方法在測(cè)點(diǎn)布置稀疏時(shí)的識(shí)別結(jié)果，僅選取點(diǎn)4, 6, 8, 10, 12, 14和16共7個(gè)點(diǎn)的加速度信號(hào)計(jì)算損傷指標(biāo)。圖9為激振點(diǎn)位于8號(hào)點(diǎn)跨中損傷時(shí)的1階振動(dòng)信號(hào)識(shí)別結(jié)果。可見(jiàn)，測(cè)點(diǎn)布置稀疏時(shí)由第1階振動(dòng)信號(hào)相對(duì)能量曲率差仍然可以很好的識(shí)別出損傷位置。

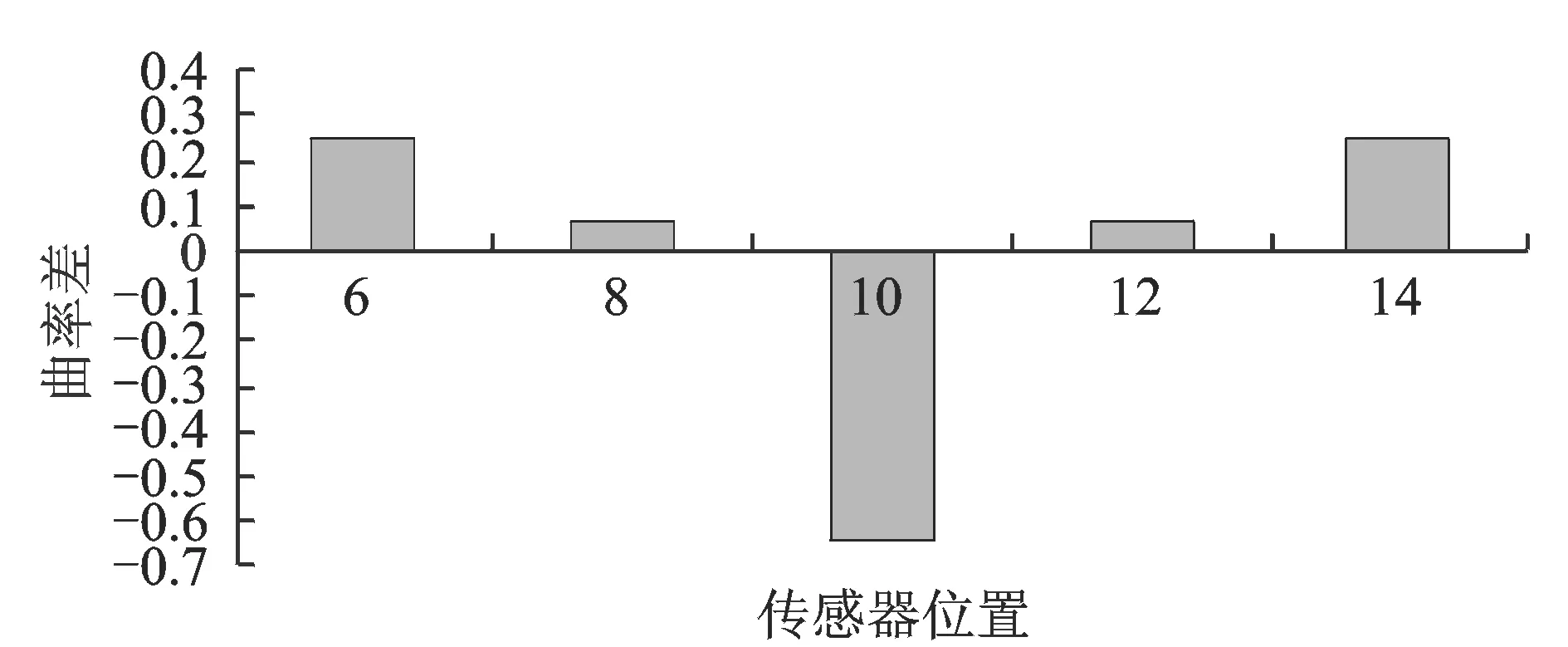
圖9 測(cè)點(diǎn)布置稀疏10號(hào)點(diǎn)處發(fā)生損傷時(shí)1階振動(dòng)信號(hào)識(shí)別結(jié)果Fig.9 Damage position-point 10: relative energy curvature differences of the first order signal under sparse measuring points

3 實(shí)驗(yàn)驗(yàn)證

在數(shù)值模擬的基礎(chǔ)上，采用硬質(zhì)PVC板材制作了簡(jiǎn)支梁模型進(jìn)行實(shí)驗(yàn)驗(yàn)證。結(jié)構(gòu)的材料參數(shù)、幾何屬性均與數(shù)值算例相同。實(shí)驗(yàn)中僅對(duì)簡(jiǎn)支梁較容易損壞的跨中部分進(jìn)行了切口損傷以模擬損傷狀態(tài)2。測(cè)點(diǎn)布置采用稀疏布置方式，激振位置選擇10號(hào)點(diǎn)即跨中位置，采樣頻率及采樣時(shí)間的設(shè)定均與數(shù)值模擬相同。實(shí)驗(yàn)現(xiàn)場(chǎng)照片如圖10所示。

圖10 實(shí)驗(yàn)現(xiàn)場(chǎng)照片F(xiàn)ig.10 Photo of experiment site

圖11(a)，(b)分別為實(shí)驗(yàn)測(cè)得的梁跨中損傷時(shí)4號(hào)點(diǎn)的加速度時(shí)程曲線及其頻譜圖。由于激振點(diǎn)位于跨中，是第2， 4階振型的節(jié)點(diǎn)，因此響應(yīng)中沒(méi)有這兩階振動(dòng)信號(hào)。

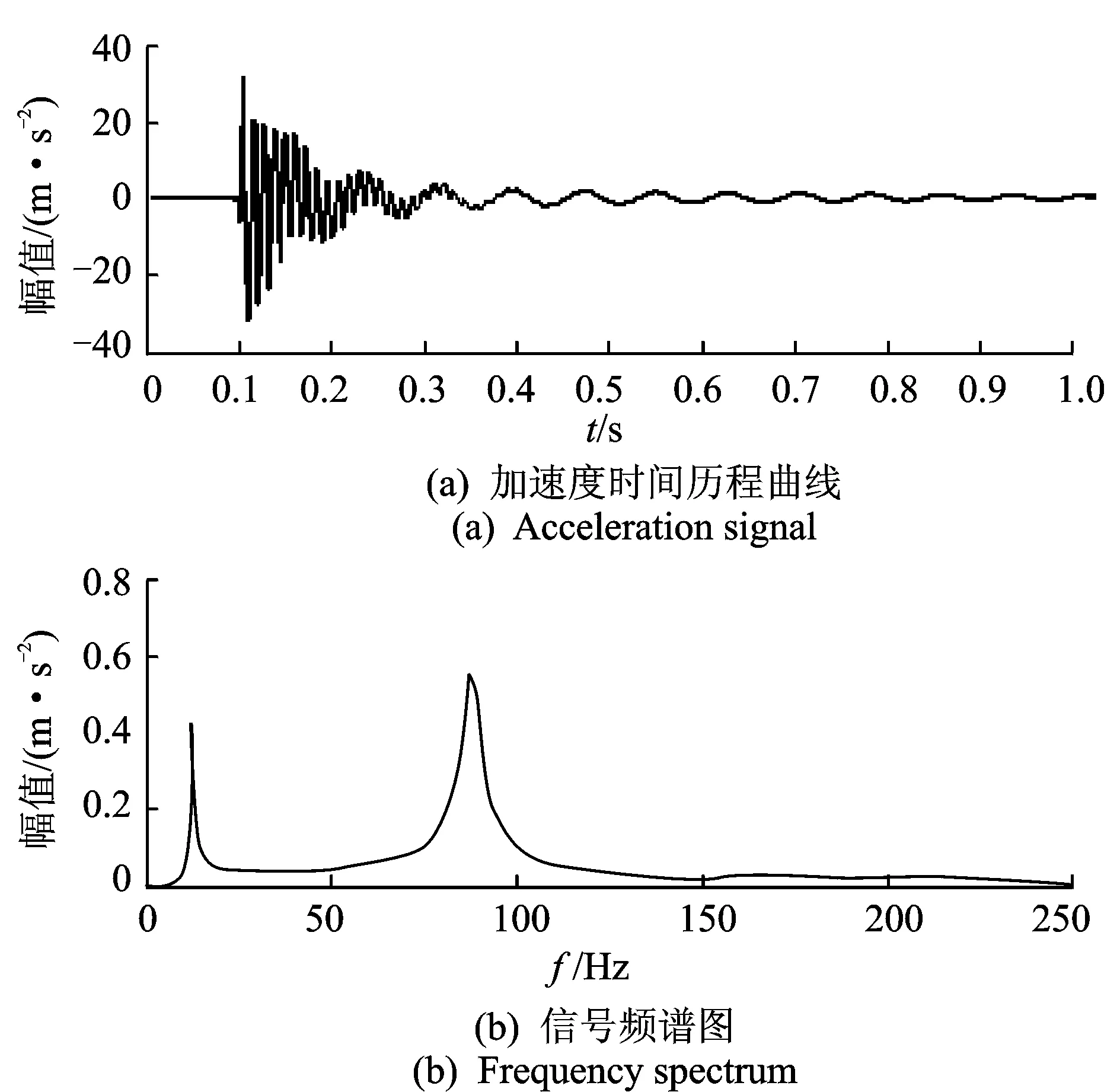
圖11 損傷梁4號(hào)點(diǎn)的加速度信號(hào)時(shí)間歷程及其頻譜圖Fig.11 Acceleration signal and frequency spectrum of point 4 under the second damage condition

采用db4小波對(duì)該信號(hào)進(jìn)行3層小波分解并重構(gòu)，各子帶重構(gòu)信號(hào)及頻譜分析結(jié)果如圖12(a)，(b)所示。分解后得到a3,d3,d2和d14個(gè)頻帶，但d3和d1兩個(gè)頻帶信號(hào)成分幅值幾乎為零，故圖中只給出a3和d2兩個(gè)子帶信號(hào)。在時(shí)間歷程上，a3和d2兩個(gè)頻帶信號(hào)成分為指數(shù)衰減形式，在頻率上分別對(duì)應(yīng)結(jié)構(gòu)第1階和第3階模態(tài)響應(yīng)。

將結(jié)構(gòu)損傷前后7個(gè)測(cè)點(diǎn)測(cè)得的振動(dòng)加速度響應(yīng)進(jìn)行小波子帶分解與重構(gòu)，選擇第1階振動(dòng)信號(hào)計(jì)算相對(duì)能量曲率差，結(jié)果如圖13所示。將圖13與圖9對(duì)比發(fā)現(xiàn)，雖然數(shù)值模擬和實(shí)驗(yàn)中選擇的激振位置不同，但其識(shí)別結(jié)果基本吻合。無(wú)論是數(shù)值模擬還是實(shí)驗(yàn)結(jié)果，信號(hào)相對(duì)能量曲率差在6， 8， 12及14測(cè)點(diǎn)位置均為正，在10號(hào)測(cè)點(diǎn)處為負(fù)，且在10號(hào)點(diǎn)變化最大，正確指示出了損傷位置。

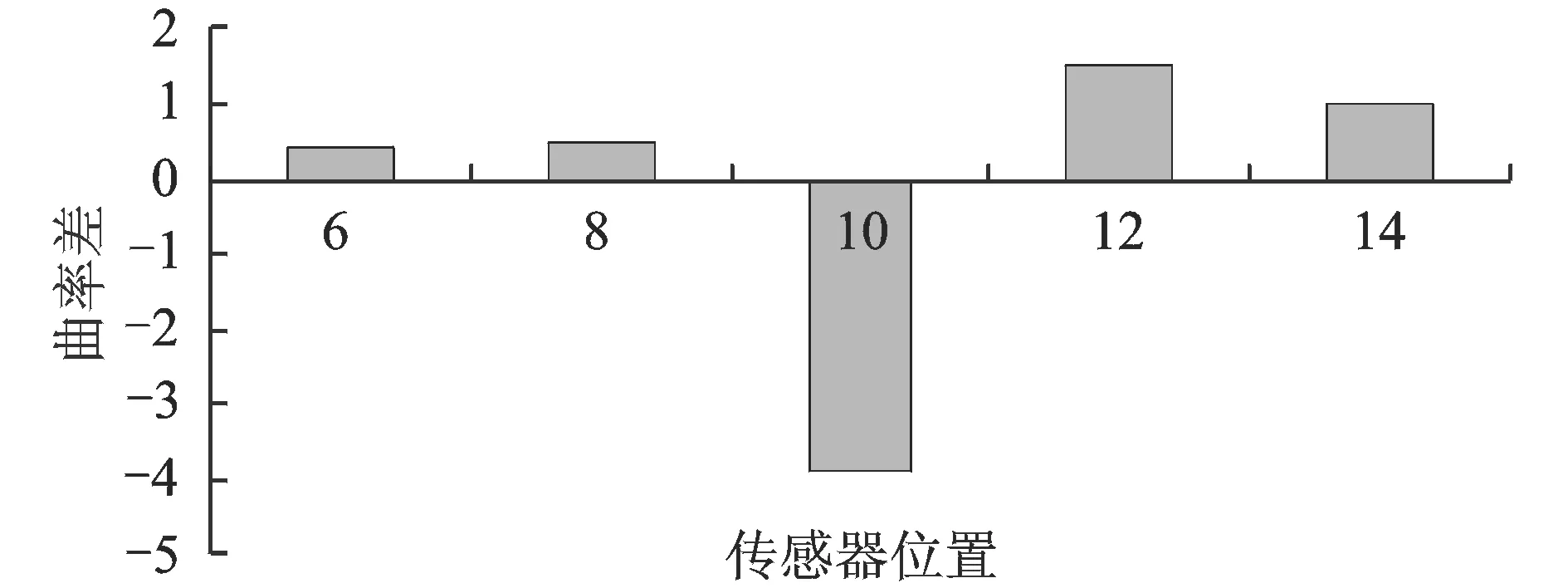
圖13 1階振動(dòng)信號(hào)相對(duì)能量曲率差實(shí)驗(yàn)結(jié)果Fig.13 The relative energy curvature differences of the first order signal (experiment result)

需要指出，以上僅采用簡(jiǎn)支梁橋?qū)Ψ椒ㄟM(jìn)行了驗(yàn)證。對(duì)于更復(fù)雜的工程結(jié)構(gòu)，模態(tài)較為復(fù)雜，尚有待于進(jìn)一步研究。

4 結(jié)束語(yǔ)

通過(guò)對(duì)一簡(jiǎn)支梁橋進(jìn)行損傷數(shù)值分析及實(shí)驗(yàn)驗(yàn)證，結(jié)果表明采用二進(jìn)離散小波變換可以對(duì)結(jié)構(gòu)在沖擊激勵(lì)下振動(dòng)響應(yīng)中疊加的多階模態(tài)信息進(jìn)行有效分離，在此基礎(chǔ)上定義的信號(hào)相對(duì)能量曲率差指標(biāo)可以對(duì)損傷進(jìn)行有效識(shí)別。同時(shí)，筆者提出的損傷識(shí)別方法具有以下優(yōu)點(diǎn)：a.具有信號(hào)分解層次易于確定、分解得到的各子帶信號(hào)物理意義較為明確等優(yōu)點(diǎn)；b.該方法避免了模態(tài)分析的復(fù)雜過(guò)程，分析過(guò)程較為簡(jiǎn)潔，同時(shí)又達(dá)到了與曲率模態(tài)差類似的效果。

[1] Hong J C, Kim Y Y, Lee H C, et al. Damage detection using the Lipschitz exponent estimated by the wavelet transform: applications to vibration modes of a beam[J].International Journal of Solids and Structures, 2002, 39(7): 1803-1816.

[2] Ovanesova A V, Suárez L E. Applications of wavelet transforms to damage detection in frame structures[J].Engineering Structures, 2004, 26(1): 39-49.

[3] 孫增壽，韓建剛，任偉新.基于曲率模態(tài)和小波變換的結(jié)構(gòu)損傷識(shí)別方法[J].振動(dòng)、測(cè)試與診斷，2005， 25(4): 263-267.

Sun Zengshou, Han Jiangang, Ren Weixin.Structural damage identification based on curvature mode and wavelet transform[J].Journal of Vibration, Measurement & Diagnosis, 2005, 25(4): 263-267.(in Chinese).

[4] 陳換過(guò)，江金壽，李劍敏，等.基于提升小波包和神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)損傷識(shí)別[J].振動(dòng)、測(cè)試與診斷，2013， 33(1): 116-121.

Chen Huanguo, Jiang Jinshou, Li Jianmin, et al.Damage detection of wing-box on lifting wavelet packet transform and neural network[J].Journal of Vibration, Measurement & Diagnosis, 2013, 33(1): 116-121.(in Chinese)

[5] Nematollahi M A, Farid M, Hematiyan M R, et al.Crack detection in beam-like structures using a wavelet-based neural network[J].Journal of Aerospace Engineering(Proceedings of the Institution of Mechanical Engineers, Part G), 2012, 226(10): 1243-1254.

[6] 孫增壽，范科舉.基于提升小波熵指標(biāo)的梁板組合橋損傷識(shí)別研究[J].振動(dòng)與沖擊，2012，31(11): 114-117.

Sun Zengshou, Fan Keju.Damage detection for a gird-slab combined bridge based on lifting wavelet entropy indexes[J].Journal of Vibration and Shock, 2012, 31(11): 114-117.(in Chinese)

[7] Sun Z, Chang C C.Statistical wavelet-based method for structural health monitoring[J].Journal of Structural Engineering, 2004, 130(7): 1055-1062.

[8] Han Jiangang, Ren Weixin, Sun Zengshou.Wavelet packet based damage identification of beam structures[J].International Journal of Solids and Structures, 2005, 42(26): 6610-6627.

[9] 范穎芳，胡志強(qiáng)，周晶，等.基于小波包分析的肋拱橋結(jié)構(gòu)損傷狀態(tài)研究[J].工程力學(xué)，2008， 25(5): 182-188.

Fan Yingfang, Hu Zhiqiang, Zhou Jing, et al.Study on damage state of ribbed arch bridge using wavelet packet analysis[J].Engineering Mechanics, 2008, 25(5): 182-188.(in Chinese)

[10]Shuichi M, Sherif B, Toshiyuki O.Wavelet packet based damage detection in beam-like structures without baseline modal parameters[J].Structure and Infrastructure Engineering, 2011, 7(3): 211-227.

[11]葛繼平，李胡生.基于小波包能量累積變異的梁橋損傷識(shí)別試驗(yàn)[J].振動(dòng)、測(cè)試與診斷，2011，31(1): 85-88.

Ge Jiping, Li Husheng.Experiment on damage detection of girder bridge using wavelet packet energy accumulated variation[J].Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 85-88.(in Chinese)

[12]楊建國(guó).小波分析及其工程應(yīng)用[M].北京: 機(jī)械工業(yè)出版社，2005：17-58.

[13]Sun Z, Chang C C.Structural damage assessment based on wavelet packet transform[J].Journal of Structural Engineering, 2002, 128(10): 1354-1361.

[14]李德葆，陸秋海.實(shí)驗(yàn)?zāi)B(tài)分析及其應(yīng)用[M].北京: 科學(xué)出版社，2001：58-87.

[15]荊龍江，項(xiàng)貽強(qiáng).基于模態(tài)分析技術(shù)的大跨度斜拉橋主梁損傷識(shí)別[J].中國(guó)鐵道科學(xué)，2007，28(6): 54-59.

Jing Longjiang, Xiang Yiqiang.Damage identification for the main girders of large-span cable-stayed bridge based on modal analysis technique[J].China Railway Science, 2007, 28(6): 54-59.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.010

*國(guó)家自然科學(xué)基金資助項(xiàng)目(51009107)；天津市基礎(chǔ)重點(diǎn)基金資助項(xiàng)目(13JCZDJC27100)；天津市青年基金資助項(xiàng)目(13JCQNJC04200)

2013-09-03；

2013-10-28

U446; TN911.6

劉習(xí)軍,男，1956年2月生，教授、博士生導(dǎo)師。主要研究方向?yàn)榉蔷€性振動(dòng)理論及應(yīng)用、橋梁振動(dòng)力學(xué)及損傷動(dòng)力檢測(cè)等。曾發(fā)表《MR-TMD減振系統(tǒng)對(duì)連續(xù)箱梁橋振動(dòng)控制研究》(《振動(dòng)與沖擊》2012年第31卷第20期)等論文。 E-mail：lxijun@tju.edu.cn