基于信號時頻分析理論識別時變模態參數實驗*

楊 凱， 于開平， 白云鶴

(哈爾濱工業大學航天學院 哈爾濱， 150001)

?

基于信號時頻分析理論識別時變模態參數實驗*

楊 凱， 于開平， 白云鶴

(哈爾濱工業大學航天學院 哈爾濱， 150001)

為研究溫度對結構模態參數的影響設計了一套溫度可控的實驗設備。在這套實驗設備提供的可控溫度環境中采集懸臂梁結構的加速度響應信號，利用基于信號時頻分析的模態參數辨識算法處理實驗數據，得到其時變模態參數，包括固有頻率和振型，以此研究溫度對其模態參數的影響。分析結果顯示了基于信號時頻分析的模態參數辨識算法在處理非平穩信號以得到結構的時變模態參數上的應用前景，更重要的是實驗數據的分析結果較好地反映了溫度對結構模態參數的影響，為熱環境下結構振動特性分析提供了可靠而且有價值的分析方法和實驗依據。

時變模態參數； 時頻分析； 懸臂梁； 溫度變化環境

引 言

對于非時變結構系統，模態參數測試分析技術已經發展得比較成熟，但針對時變結構系統的相應研究工作較少[1-2]，而模態參數能夠幫助深入理解結構的動態特性。在航空航天領域，飛行器由于高速飛行會引起嚴重的氣動加熱作用而承受惡劣的高溫工作環境，高溫作用必然會引起結構模態參數的變化[3-5]。由于受制于模態參數辨識算法的研究狀況，文獻[3-5]中只研究了恒定高溫環境中溫度對結構模態參數的影響，而忽略了整個溫度變化過程中模態參數變化。相比于時域模態參數辨識算法，頻域模態參數辨識算法有更好的抗噪聲等性能，工程實際中應用更加廣泛[6]。現代信號處理方法中信號時頻分析方法的研究已經相對成熟，時頻分析方法能夠較好地處理非平穩信號且同樣有較好的抗噪聲能力，相對于頻域分析方法能給出信號時域特征信息。鑒于此，信號時頻分析方法很自然地被引入到模態參數辨識領域中來[7-13]。文獻[8]研究了Gabor變換在模態參數辨識中的應用，指出這種算法可以較好地處理平穩和非平穩振動得到時不變模態參數。由材料力學可知，拉伸或者壓縮應力的存在會影響結構的固有頻率，文獻[13]利用小波分析方法處理了桿結構在持續加載過程的振動響應，分析了結構一階固有頻率的變化情況。上述文獻都僅僅關注時頻分析方法在時不變模態參數辨識中的應用，而且鮮有文獻報道時變結構中模態振型的情況。為此，筆者總結了上述文獻[7-12]中基于時頻分析方法的模態參數辨識算法，并利用基于信號時頻分析的模態參數辨識算法分析了在溫度變化環境中一TC4鈦合金懸臂梁的前4階模態信息。

1 算法過程簡介

基于信號時頻分析的模態參數辨識算法[7-12]可總結如下：

1) 引入一種合適的線性時頻變換方法，諸如Gabor變換或小波變換，時域信號qi(t)(i=1, 2, …,M)在時頻域內表示為qi(t,f),(i= 1, …,M)。不失一般性，筆者選用短時傅里葉變換(short time Fourier transform，簡稱STFT)。

(1)

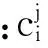
(2)

4) 結構的固有頻率可以直接由時頻脊線讀取；如果信號不是自由衰減信號且非平穩，那么對信號時頻分解所得的單模態信號進行奇異值分解，還進一步得到結構的阻尼比[12]。

2 實驗及其結果分析

2.1 實驗

圖1 實驗設備圖Fig.1 The laboratory experimental setup

實驗選用尺寸為380mm×38mm×6mm的TC4鈦合金懸臂梁作為試件，如圖1所示。試件通過夾具固定于型號為DC-2200-26的電動振動臺水平滑臺上，通過振動臺提供隨機白噪聲形式的基礎激振，利用型號為Endevco?6327M70d的3個加速度傳感器采集試件在整個實驗環境溫度受控過程中的加速度響應信號(這3個加速度傳感器在650 ℃以下溫度環境中能穩定工作)。試件直接受熱面的溫度由布置在試件表面的熱電偶采集，并反饋至可編程式邏輯控制器，控制器根據預設的升溫曲線實時控制紅外石英燈陣的加熱功率，由此實現預設的溫升環境。整個實驗框圖如圖2所示，圖2中3個傳感器從上到下順序編號為①,②和③，對應于辨識算法介紹中涉及到時域信號qi(t)(i= 1, …,M)。本實驗中，懸臂梁表面溫度被控制在90 s內由室溫(大約22 ℃)線性升高至400 ℃，然后保持400 ℃大約75 s。實際溫度變化過程如圖3所示。3個熱電偶安裝于3個傳感器位置的背面，中間位置作為溫控參考點，其余兩個用于觀察。通過理論計算，試件的第4階固有頻率是1 102 Hz，由此在本實驗中設置采樣頻率為2 560 Hz。

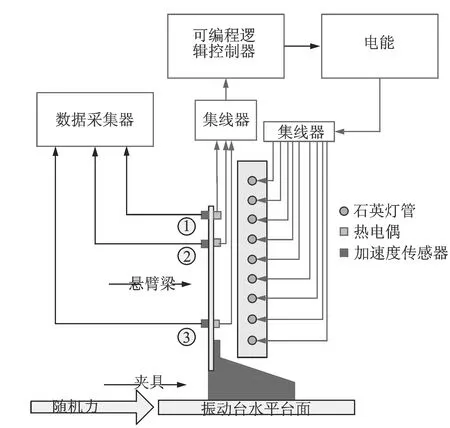
圖2 實驗設備框圖Fig.2 The schematic framework of the laboratory setup

圖3 受控的溫度變化曲線Fig.3 The controlled temperature curves.

在該實驗進行之前，在同樣夾持條件下，利用基于信號時頻分析的模態參數辨識算法處理此懸臂梁在錘擊激勵下的加速度響應信號得到其前4階模態信息，以此作為溫度變化環境中實驗的模態分析結果的參考值，頻率和振型結果如圖4所示,圖中藍色實線是利用Euler-Bernoulli梁理論導出的懸臂梁前4階振型；紅色離散點是利用錘擊法實驗分析得到的懸臂梁振型。

圖4 室溫下懸臂梁的前4階模態信息Fig.4 The former four-order modes of the cantilever beam

2.2 實驗結果分析

文獻報道，溫度對結構動態特性的影響主要有兩個因素：a.溫度直接影響結構材料的彈性模量，一般溫度升高，彈性模量下降，結構剛度下降，固有頻率下降[3-5]；b.溫度分布不均勻導致熱應力，熱應力產生結構附加剛度，固有頻率升高[14]。圖5展示了第2個加速度傳感器采集到在溫度持續變化過程中懸臂梁響應的時頻譜。由于第3, 4兩階固有頻率變化比較明顯，故圖示于圖6。如圖5, 6所示，溫度對此TC4鈦合金懸臂梁的前4階固有頻率的影響比較明顯：溫度升高，前4階固有頻率都下降。由此推斷，在這種溫度變化的熱環境中溫度對TC4鈦合金的彈性模量的影響是主要的。

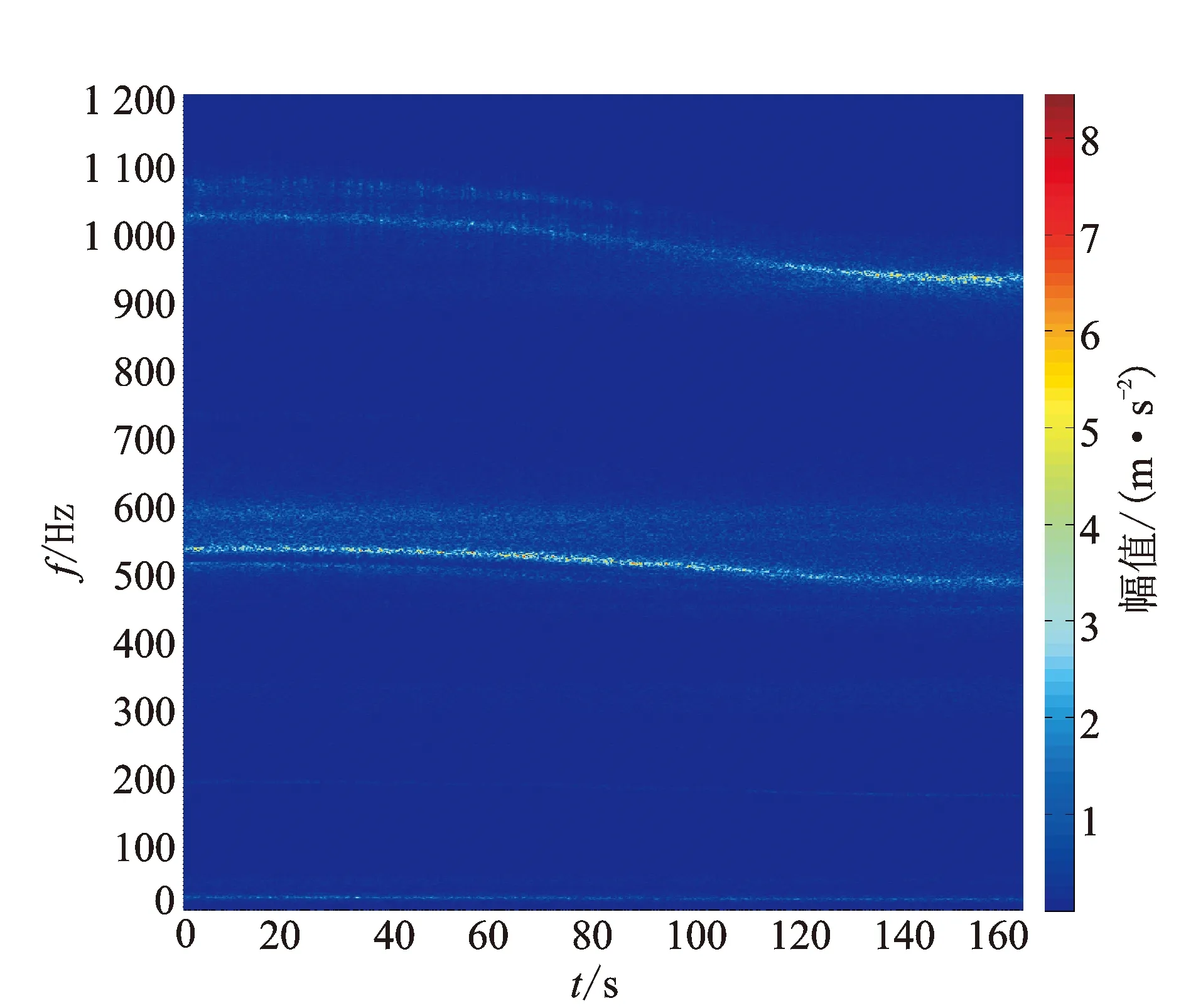
圖5 中間傳感器采集到信號的時頻譜圖Fig.5 The STFT spectrogram of signal collected by the middle sensor

圖6 溫度變化環境中懸臂梁的第3, 4階固有頻率Fig.6 The third and fourth order natural frequencies of the cantilever beam in the temperature-varying environment

利用基于信號時頻分析的模態參數辨識算法處

理實驗數據并以此分析溫度對此TC4鈦合金懸臂梁振型的影響，結果如圖7所示。圖7以第3階振型為例，說明如何利用基于信號時頻分析的模態參數辨識算法估計結構的時變振型。

利用各測試點響應數據時頻譜中第3階固有頻率脊線提取的結果，依據式(1)得到2號和3號測試點在每一時刻與參考點之間的幅值比，即結構第3階振型向量的絕對值，及其隨時間變化的關系，如圖7(a)所示；依據式(2)得到其他兩個測試點信號與參考信號之間相位差，如圖7(b)所示，用以確定振型向量方向(正負)。綜合圖7中的這兩個子圖得到整個實驗過程中懸臂梁第3階模態振型隨時間的變化情況。采用同樣的辦法，依次可以得到其他3階振型。圖8對比了第60 s和第120 s結構的前4階振型，從中可以清晰地看出，溫度對試件的前4階振型影響很細微。

在筆者所述的實驗條件下，由于結構受熱導致膨脹變形，不會受到約束的限制；而且金屬材料試件的熱導率較大，試件厚度方向上并不會存在非常大的溫度梯度，因此結構內部熱應力水平處于很低的水平，那么結構剛度矩陣的變化就可以認為只受彈性模量的影響。金屬材料彈性模量與溫度變化的關系是近似線性的，同時考慮到該結構質量矩陣受溫度影響的程度可以忽略不計。根據模態分析的基本理論，很容易得出結論：在上述情況下，系統廣義特征值隨剛度陣線性變化，而各特征值對應的特征向量保持不變；即：結構各階固有頻率隨溫度變化而變化，但模態振型并不會受到溫度的影響。

圖7 利用基本信號時頻分析的模態參數辨識算法提取第3階振型的過程Fig.7 The procedure of extracting the third-order mode shape by the TFR-based modal parameter identification method

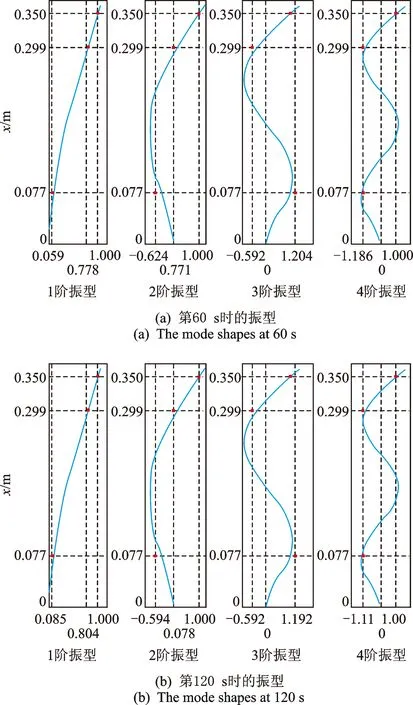
圖8 實驗過程中兩個時刻對應的懸臂梁振型Fig.8 The mode shapes of the cantilever beam at two instant times

3 結束語

筆者利用基于信號時頻分析的模態參數辨識算法，處理在溫度變化環境中TC4鈦合金懸臂梁的振動加速度響應信號，得到該結構的前4階時變模態信息。結果顯示持續變化的溫度對此懸臂梁的前4階固有頻率影響比較明顯：溫度升高，固有頻率下降，而溫度對筆者所述的溫度變化環境中的TC4鈦合金懸臂梁的固有振型影響幾乎可以忽略。另一方面，分析結果也顯示，基于信號時頻分析的模態參數辨識算法有較好的工程應用前景。

此外，時頻脊線的提取過程(即圖7所用數據)采用了最原始的峰值提取法，執行效率較低并有一定的主觀因素，這在實際應用中是不可取的，進一步的工作將在自動提取理論方法方面深入開展。

[1] Poulimenos A G, Fassois S D.Parametric time-domain methods for non-stationary random vibration modeling and analysis——a critical survey and compassion[J].Mechanical Systems and Signal Processing, 2006, 20(4): 763-816.

[2] Poulimenos A G, Fassois S D.Output-only stochastic identification of a time-varying structure via functional series TARMA models[J].Mechanical Systems and Signal Processing, 2009, 23(4): 1180-1120.

[3] Kehoe M W, Deaton V C.Correlation of analytical and experimental hot structure vibration results[R]. California: NASA Technical Memorandum 104269, 1993.

[4] Kehoe M W, Snyder H T.Thermoelastic vibration test techniques[R].California: NASA Technical Memorandum 101742, 1991.

[5] Jeon B H, Kang H W, Lee Y S.Free vibration characteristics of thermally loaded rectangular plates[J].Key Engineering Materials, 2011, 478: 81-86.

[6] 劉宗政，陳懇，郭隆德,等. 基于環境激勵的橋梁模態參數識別[J]. 振動、測試與診斷，2010, 30(3)： 300-303.

Liu Zongzheng, Chen Ken, Guo Longde, et al. Modal parameter identification of a bridge under ambient excitation[J].Journal of Vibration, Measurement & Diagnosis, 2010, 30(3): 300-303.(in Chinese)

[7] Lardies J, Gouttebroze S. Identification of modal parameters using the wavelet transform[J].International Journal of Mechanical Sciences, 2002, 44(11): 2263-2283.

[8] Zhang Z Y, Hua H X, Xu X Z, et al.Modal parameter identification through Gabor expansion of response signals[J].Journal of Sound and Vibration, 2003, 266(5): 943-955.

[9] Le T P, Argoul P. Continuous wavelet transform for modal identification using free decay response[J].Journal of Sound and Vibration, 2004, 277(1): 73-100.

[10]Yan B F, Miyamoto A, Bruhwiler E. Wavelet transform- based modal parameter identification considering uncertainty[J].Journal of Sound and Vibration, 2006, 291(1): 285-301.

[11]Li Zhuang, Crocker M J. A study of joint time-frequency analysis-based modal analysis[J].IEEE Transactions on Instrumentation and Measurement, 2006, 55(6): 2335-2342.

[12]Le T P, Paultre P.Modal identification based on the time-frequency domain decomposition of unknown-input dynamic tests[J].International Journal of Mechanical Sciences, 2013, 71: 41-50.

[13]Wang Chao, Ren Weixin, Wang Zuocai, et al.Instantaneous frequency identification of time-varying structyres by continuous wavelet transform[J].Engineering Structures, 2013, 52: 17-25.

[14]Zhang Deyi, Bao Yuequan, Li Hui, et al. Investigation of temperature effects on modal parameters of the China national aquatics center[J]. Advances in Structural Engineering, 2012, 15 (7): 1139-1153.

10.16450/j.cnki.issn.1004-6801.2015.05.012

*國家自然科學基金資助項目(11172078)

2013-09-20；

2013-10-17

O327; U446

楊凱，男，1986年12月生，博士生。主要研究方向為振動信號處理、時變模態參數辨識等。曾發表《Modal parameter extraction based on Hilbert transform and complex independent component analysis with reference》(《Mechanical Systems and Signal Processing》 2013, Vol.40, No.1)等論文。 E-mail: yg.hit@hotmail.com