壓縮機轉子系統的振動可靠性靈敏度設計*

朱麗莎， 張義民， 杜尊令

(1.東北大學機械工程與自動化學院 沈陽，110819) (2.沈陽機床股份有限公司中捷立式加工中心 沈陽，110141)

?

壓縮機轉子系統的振動可靠性靈敏度設計*

朱麗莎1， 張義民1， 杜尊令2

(1.東北大學機械工程與自動化學院 沈陽，110819) (2.沈陽機床股份有限公司中捷立式加工中心 沈陽，110141)

為了對壓縮機類復雜的轉子系統進行可靠性靈敏度設計，探討可靠度與基本隨機變量之間的關系，得到不同隨機變量對可靠性的影響程度。通過引入隔離裕度和放大因子的概念，在轉子系統動力響應的基礎上，預測系統實際隔離裕度與許用隔離裕度。首先，根據許用隔離裕度不超過實際的隔離裕度的關系準則，針對壓縮機類轉子系統提出了一種基于共振失效的振動可靠性模型；然后，利用神經網絡模型代替了有限元模型建立了復雜結構的可靠度與基本隨機變量的強非線性關系；最后，以某齒輪轉子系統為例，應用可靠性設計理論求解某轉子系統危險位置的可靠度，應用可靠性靈敏度理論得到了系統均值靈敏度和方差靈敏度。

可靠性； 隔離裕度； 靈敏度； 振動； 轉子系統

引 言

轉子系統的可靠性研究是近代機械領域研究的熱門課題。目前，對轉子系統的可靠性建模，主要分為如下幾類：a.基于碰摩失效的可靠性模型,轉子的特殊位置在工作狀態下由于振動超限造成與定子之間的碰撞摩擦，如轉子系統的質量慢變[1]、不對中[2-3]和油膜振蕩失穩[4-5]都會造成系統失效；b.基于疲勞失效的可靠性模型,轉子由于受到復合應力的作用產生疲勞破壞，在大量疲勞強度分布試驗的基礎上，采用應力-強度可靠性分析方法，對疲勞壽命進行估算[6]；c.基于頻率干涉的可靠性模型[7],根據轉子系統的固有頻率與激振頻率差的絕對值不超過規定值的關系準則，定義了轉子系統共振問題的可靠性模式和系統的可靠度；d.基于裂紋失效的轉子可靠性模型。胥建群等[8]基于斷裂力學的理論對汽輪機轉子系統進行了概率分析，將裂紋擴展速率、初始裂紋尺寸和應力變化幅值考慮成獨立隨機變量，對含有初始缺陷的汽輪機轉子進行了壽命預測。

參照美國石油協會標準，筆者提出了一種基于共振失效的振動可靠性模型。此模型引入了隔離裕度和放大因子(amplification factor,簡稱AF)的概念，通過轉子系統的動力響應曲線計算出實際的隔離裕度和許用的隔離裕度。根據轉子系統的許用隔離裕度不超過實際的隔離裕度的關系準則，建立了系統的可靠性模型，并基于Edgeworth級數和四階矩方法，選取某轉子系統的危險位置進行了可靠性求解與可靠性靈敏度設計。

1 共振失效機理

API617是美國石油學會針對石油、化學和氣體工業用的軸流類、離心類壓縮機以及膨脹機-壓縮機的整體設計、試驗、安裝和維護等制定的標準。根據API617中動力學設計的要求，轉子系統在橫向振動分析過程中，有兩種情況會發生共振：a.放大因子大于等于2.5；b.轉子系統的實際隔離裕度小于許用的隔離裕度。兩種情況同時發生則認為轉子系統發生了共振失效。

1.1 放大因子AF的計算方法

轉子第1階臨界轉速處，放大因子AF定義為

(1)

圖1 放大因子計算示意圖Fig.1 The calculation diagram of amplification factor

放大因子AF的計算示意圖如圖1所示，并不代表任何實際的轉子系統的響應曲線。圖中：Nc1為轉子第1階臨界轉速，中心頻率，單位r/min；Ac1為在Nc1處的振幅；Ncn為轉子第n階臨界轉速；Acn為在Ncn處的振幅；N1為0.707倍振幅峰值時對應的初始轉速；N2為0.707倍振幅峰值時對應的終止轉速；N2-N1為在“半功率”點峰值寬度；SM為隔離裕度；CRE為臨界響應區。

1.2 許用隔離裕度SM′的計算方法

1) 如果在某一臨界轉速處的AF<2.5，說明該響應在此臨界轉速下不會發生振動，因此不需要計算隔離裕度。

2) 如果在某一臨界轉速處的AF≥2.5，并且此臨界轉速低于工作時的最小轉速，該SM′(作為最小轉速的百分數)用式(1)計算，得到的值與16相比，取較小者。最小轉速為工作轉速的85%。

(2)

3) 如果在某一臨界轉速處的AF≥2.5，并且此臨界轉速高于工作時的最大連續轉速，該SM′(作為最大連續轉速的百分數)用式(2)計算，得到的值與26相比，取較小者。最大連續轉速取工作轉速的115%。

(3)

1.3 實際隔離裕度SM的計算方法

實際隔離裕度與工作轉速和臨界轉速有關，分為兩種情況。

1) 當工作轉速Nw小于某一臨界轉速Ncn，則實際隔離裕度為

(4)

其中:Nwmax為最大連續工作轉速，為工作轉速Nw的115%。

2) 當工作轉速Nw大于某一臨界轉速Ncn，則實際隔離裕度為

(5)

其中：Nwmin為最小連續工作轉速，為工作轉速Nw的85%。

在確定了轉子的臨界轉速以及振動響應曲線后，就可以計算出系統的放大因子(AF)、實際隔離裕度(SM)和許用隔離裕度(SM′)，進一步判斷系統是否失效，流程圖如圖2所示。

圖2 程序流程圖Fig.2 Program flow chart

2 可靠性與可靠性靈敏度分析

2.1 極限狀態方程

當計算的隔離裕度大于規定的隔離裕度時，系統安全，反之則系統發生共振失效。因此，當工作轉速低于臨界轉速時，極限狀態方程的表示為兩種形式。

1)SM′<26時

(6a)

2)SM′>26時

(6b)

當工作轉速高于臨界轉速時，極限狀態方程的表示為兩種形式。

1)SM′<16時

(6c)

2)SM′>16時

(6d)

其中：X為由系統基本參數組成的隨機變量向量。

采用人工神經網絡技術[9]可以模擬得到函數Ncn(X)，N1(X)，N2(X)與基本隨機變量的關系式，進而得到極限狀態方程g(X)與基本隨機變量之間的非線性顯性關系式。

2.2 可靠性設計

根據概率論和隨機攝動法的相關知識，狀態函數g(·)的前四階矩[2-4]為

其中：C3和C4分別表示隨機向量的三階中心矩和四階中心矩;(*)k=(*)?(*)?…(*)為(*)的kronecker冪。

可靠性指標定義為

(11)

根據Edgeworth級數和四階矩技術，得到轉子系統的可靠度計算公式為

R(β)=P(SM≥SM′)=P(g(X)≥0)=1-F(-β)

(12)

函數F(·)的表達式可以根據Edgeworth級數展開為

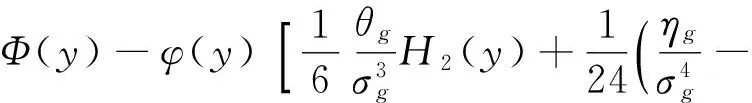
(13)

其中：y=-β；Ф(·)為標準正態分布函數；θg，ηg分別為狀態函數的三階矩和四階矩；Hi(y)為i階Hermite多項式，其遞推關系為

(14)

2.3 可靠性靈敏度設計

可靠度對基本隨機變量均值的靈敏度為

(15)

(16)

其中：In為n×n維單位矩陣;Un×n為置換矩陣;其維數為n2×n2并且每行和每列只有一個元素“1”;“?”表示向量矩陣之間的Kronecker乘積。

可靠度對基本隨機變量方差的靈敏度為

(17)

在進行結構設計時，設計因素往往很多，而且各因素對結構失效的影響程度又各不相同，影響可靠性的因素之間存在單位不統一的問題，因此需要將可靠性靈敏度進行無量綱化，表示為

(18)

(19)

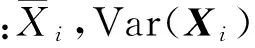
3 算 例

某齒輪轉子系統軸承處的不平衡響應曲線如圖3所示。

當臨界轉速低于工作轉速時，定義左軸承處共振失效的極限狀態方程為

(20)

其中：X為由系統基本參數組成的隨機變量向量，X=[β,α,L,k,U]T各個基本隨機變量的前四階矩如表1所示；工作轉速Nw假設為基本隨機變量，和Nc1(X),N1(X),N2(X)函數均不相關。

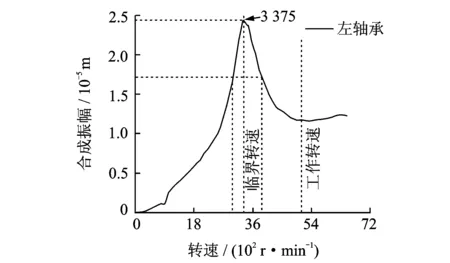
圖3 軸承處的不平衡響應曲線Fig.3 Unbalance response curve of bearing

表1 基本隨機變量的前四階矩

將均值代入式(17)可以得到系統的實際隔離裕度與要求的隔離裕度分別為SM=22.201 5；SM′=10.078 1。

因此在隨機變量取均值時，系統是安全的。

有限元模型較復雜，用一次確定性的有限元模型進行可靠性設計，假設做106次隨機抽樣，則需要大約54 Y的時間，這是不符合實際的。因此，筆者在有限樣本的基礎上，采用神經網絡模型代替有限元模型，基于矩方法和Edgeworth級數方法進行可靠性設計。

人工神經網絡采用5-8-1的形式，隨機抽樣共進行100次的拉丁超立方試驗，在達到允許誤差后，得到的神經網絡模型可以代替有限元模型。在基本隨機變量均值附近重新設計20組檢驗樣本，將檢驗樣本分別帶入有限元模型和神經網絡模型，極限狀態函數誤差如圖4所示。

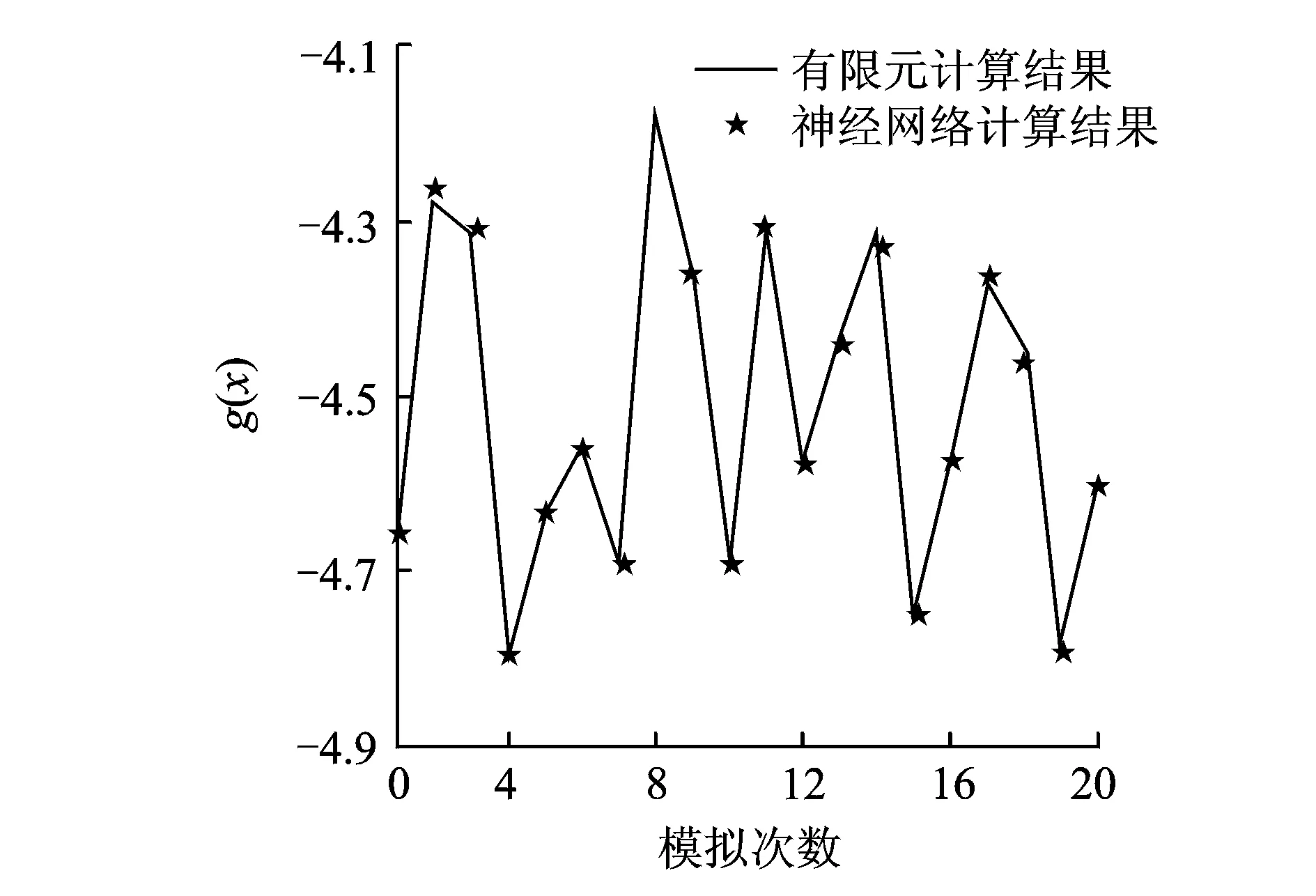
圖4 有限元模型與神經網絡模型對比結果Fig.4 Comparison of the results between FEM and ANN model

3.1 可靠度計算

基于Edgeworth級數和四階矩方法對系統進行可靠度求解，得到系統不會發生共振失效的概率。

可靠性指標為β=3.108 2；可靠度為RE=0.999 278。采用蒙特卡洛抽樣方法[10]計算，模擬次數為N=100萬次，得到的可靠度為RMCS=0.996 367(N=106)。

通過Edgeworth級數方法得到的可靠度RE與采用蒙特卡洛法得到的可靠度RMCS的誤差為

通過計算得知，采用Edgeworth級數方法計算可靠度與蒙特卡洛方法的結果誤差很小，吻合程度高。但若計算過程全部采用蒙特卡洛方法效率低，采用神經網絡與Edgeworth級數結合的方法可以大大提高計算效率[11]。此方法還可以計算系統對基本隨機變量的可靠性靈敏度。

3.2 可靠性靈敏度計算

可靠性對基本隨機參數向量Xi均值和方差的靈敏度無量綱化后分別表示為

通過計算結果發現，隨著均值的增加，系統可靠度增加的基本隨機變量為中心距、不平衡量和工作轉速。隨著均值的增加,系統可靠度降低的基本隨機變量為螺旋角、方位角和嚙合剛度。

根據各參數無量綱后的均值和方差的計算結果畫出靈敏度的直方圖如圖5，6所示。通過直方圖可以形象直觀地看到，對系統可靠度影響最大的參數為工作轉速，其次為中心距、方位角、不平衡、螺旋角及嚙合剛度。

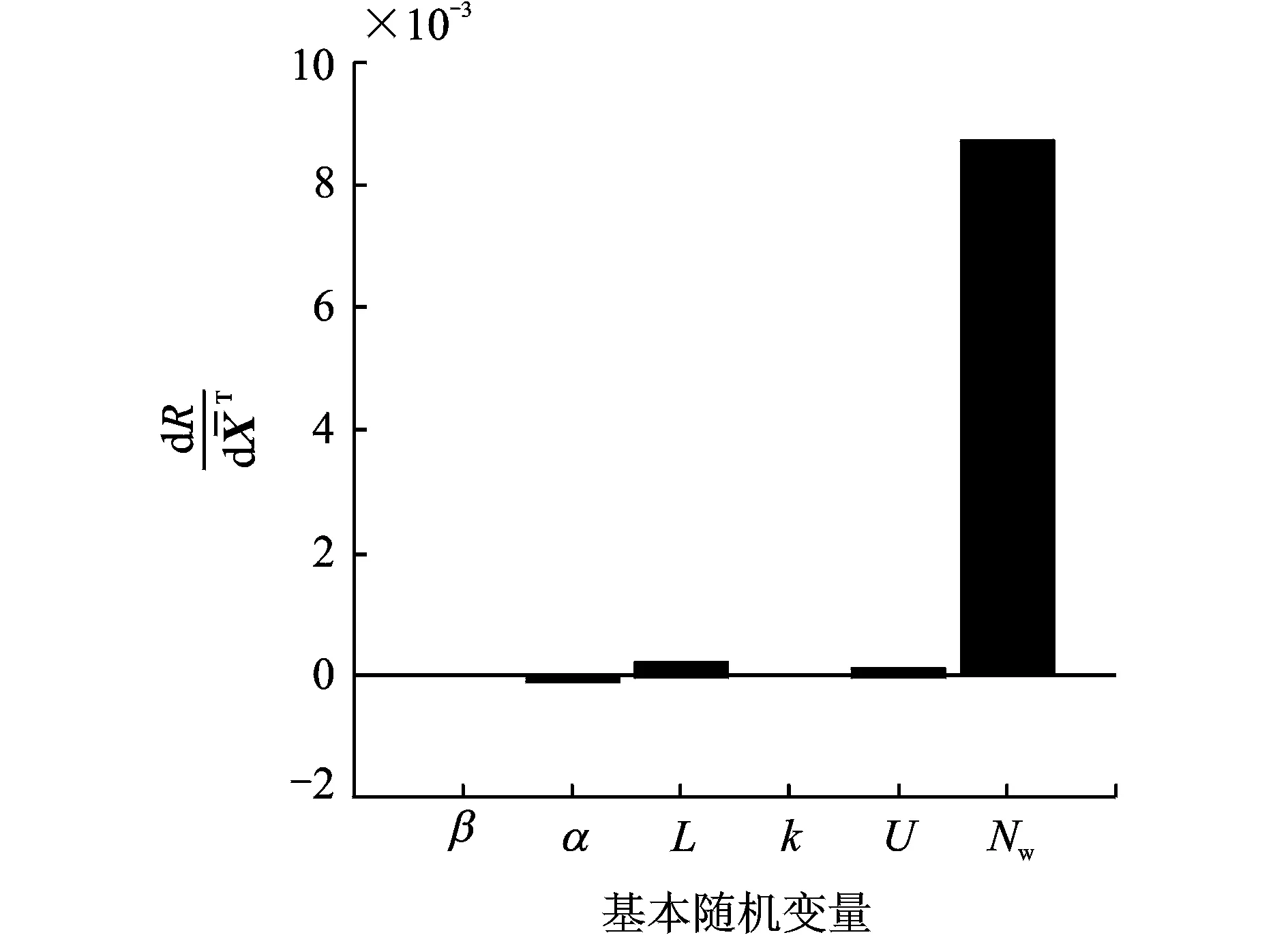
圖5 可靠度對基本隨機變量均值的靈敏度Fig.5 Reliability sensitivity to the mean value of parameters

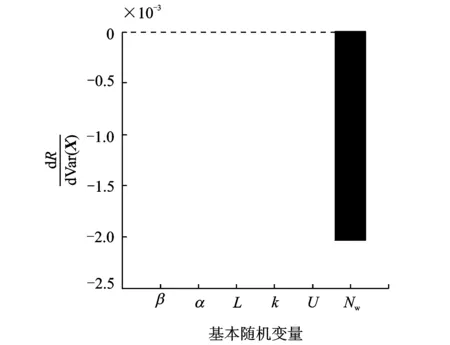
圖6 可靠度對基本隨機變量方差的靈敏度Fig.6 Reliability sensitivity to the variance of parameters

4 結 論

1) 筆者提出的共振失效依據API標準在工作轉速臨近臨界轉速的工況下，根據響應結果曲線進行的二次判定。此方法適用于壓縮機和膨脹機類的轉子系統建立失效判據。

2) 用神經網絡模型代替有限元模型，可以降低求解樣本的時間，為大型復雜系統的可靠性求解提供了有效的解決途徑。

3) 對實際樣本數量不足以統計確定概率分布的情況，基于矩方法和Edgeworth級數的可靠性設計，可以快速準確得到系統可靠度、均值靈敏度和方差靈敏度以及各參數對系統影響排序；針對壓縮機類轉子系統，在實際工作中最需要注意工作參數、其次是制造和安裝參數，最后是嚙合參數。

[1] 王宗勇, 吳敬東, 聞邦椿. 質量慢變轉子系統的松動與碰摩故障研究[J]. 振動工程學報, 2005, 18(2): 167-171.

Wang Zongyong, Wu Jingdong, Wen Bangchun. Research on pedestal looseness and rub-impact faults of rotor system with slowly varying mass [J]. Journal of Vibration Engineering, 2005, 18(2): 167-171. (in Chinese)

[2] 陳果, 李興陽. 航空發動機整機振動中的不平衡-不對中-碰摩耦合故障研究[J]. 航空動力學報, 2009, 24(10): 2277-2284.

Chen Guo, Li Xingyang. Study on imbalance-misalignment-rubbing coupling faults in aero-engine vibration [J]. Journal of Aerospace Power, 2009,24(10): 2277-2284. (in Chinese)

[3] 李明. 轉角不對中故障的轉子系統非線性動力學特征[J]. 振動、測試與診斷, 2011,31(5):552-556.

Li Ming. Nonlinear dynamics characteristics of rotor system with angular misalignment[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 552-556. (in Chinese)

[4] Wang K S, Chen C S, Huang J J. Dynamic reliability behavior for sliding wear of carburized steel[J]. Reliability Engineering & System Safety, 1997, 58(1): 31-41.

[5] 荊建平, 孟光, 孫毅, 等. 油膜振蕩下轉子疲勞的損傷力學研究[J]. 機械工程學報, 2004, 40(6): 5-9.

Jing Jianping, Meng Guang, Sun Yi, et al. Study on the fatigue damage of a rotor under oil-whip by continuum damage mechanics[J]. Chinese Journal of Mechanical Engineering, 2004, 40(6): 5-9. (in Chinese)

[6] Sorensen J D, Toft H S. Probabilistic design of wind turbines[J]. Energies, 2010, 3(2): 241-257.

[7] 張義民, 蘇長青, 聞邦椿. 轉子系統的頻率可靠性分析[J]. 振動工程學報, 2009, 22(2): 218-220.

Zhang Yimin, Su Changqing, Wen Bangchun. Natural frequency reliability analysis of rotor system[J]. Journal of Vibration Engineering, 2009, 22(2): 218-220. (in Chinese)

[8] 胥建群, 周克毅, 陳錦濤. 基于概率斷裂力學汽輪機轉子可靠性研究[J]. 汽輪機技術, 2006, 48(5): 358-360,363.

Xu Jianqun, Zhou Keyi, Chen Jintao. Reliability Study of steam turbine rotor based probability fracture mechanics[J]. Turbine Technology, 2006, 48(5): 358-360,363. (in Chinese)

[9] Cheng Jin, Cai C S, Xiao Rucheng. Application of artificial neural networks to the response prediction of geometrically nonlinear truss structures[J]. Structural Engineering and Mechanics, 2007, 26(3): 251-262.

[10]Fan Haijian, Liang Robert. Reliability-based design of axially loaded drilled shafts using Monte Carlo method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(14): 2223-2238.

[11]朱麗莎, 張義民, 盧昊, 等. 基于神經網絡的轉子振動可靠性靈敏度分析[J]. 計算機集成制造系統, 2012, 18(1): 149-155.

Zhu Lisha, Zhang Yimin, Lu Hao, et al. Reliability sensitivity analysis of rotor vibration based on neural network[J]. Computer Integrated Manufacturing Systems, 2012, 18(1): 149-155. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.019

*國家自然科學基金資助項目(U1234208);中央高校基本科研業務費資助項目(N120303002)；遼寧省科技資助項目(20131032)

2013-11-22；

2014-02-27

TB122; TB114.3; TB123

朱麗莎，女，1986年12月生，博士生。主要研究方向為機械可靠性設計。曾發表《直齒輪耦合轉子系統的振動可靠性研究》(《振動、測試與診斷》 2013年第33卷第2期)等論文。 E-mail：neulisachu@163.com