遺忘因子在SINS/GPS/BDS/EC組合導航自適應濾波中的應用*
周坤芳 于 波
(海軍陸戰學院 廣州 510430)
?
遺忘因子在SINS/GPS/BDS/EC組合導航自適應濾波中的應用*
周坤芳 于 波
(海軍陸戰學院 廣州 510430)
通過建立SINS/GPS/BDS/EC聯邦卡爾曼濾波器,引入遺忘因子的自適應濾波算法,以解決常規濾波發散問題,提高組合導航定位精度。仿真分析,相對于常規濾波,帶有遺忘因子的自適應濾波對于濾波發散現象起到了明顯控制作用,體現出了較高的精度和較強的魯棒性。
組合導航; 自適應濾波; 遺忘因子
Class Number U666.11
1 引言
采用多種導航手段進行組合,取長補短,降低對單一導航系統器件的精度要求,提高系統的可靠性和容錯性,也是導航發展的一個方向[1~2]。通過采用間接法卡爾曼濾波算法和聯邦卡爾曼濾波器結構,研究建立SINS/GPS/BDS/EC組合導航系統,以提高水下航行器導航精度。
2 SINS/GPS/BDS/EC聯邦卡爾曼濾波器
3 基于遺忘因子估計的自適應卡爾曼濾波
自適應濾波就是利用前一時刻所獲得濾波器參數的結果,自動調節目前時刻的濾波參數,以適應信號和未知的噪聲隨時間變化的統計特性,從而實現最優濾波。
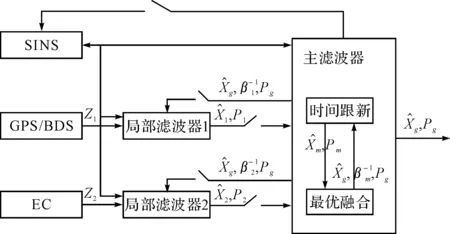
圖1 SINS/GPS/BDS/EC聯邦卡爾曼濾波器
3.1 基于遺忘因子估計的自適應濾波
自適應濾波器(Adaptive Kaiman Filter,AKF)大致可分為三類[5~6]:基于遺忘因子估計的AKF、基于噪聲統計特性估計的AKF算法和基于濾波增益矩陣估計的AKF算法。采用基于遺忘因子估計的AKF,通過加大新觀測數據的作用,減小老舊觀測數據的影響。當所選數學模型不精確或物理模型系統在運行過程中有所改變時,新近觀測數據更能反映實際情況,而老舊觀測數據不應再起作用,應該被“遺忘掉”。因此,基于遺忘因子估計的AKF利用“新息”中的有效信息,對變動過程參數具有更強的魯棒性,估計值精度較常規卡爾曼濾波也有較大提高。
常規卡爾曼濾波算法的時間更新過程[6~8]:
(1)
當每獲得一個新的量測值時,就將其與系統推算出的預測量測值進行對比,對預測值進行更新,得到最優估計。當模型參數與過程參數有較大偏差時,會影響到濾波器的精度,使卡爾曼濾波精度下降,甚至發散。而采用變化的遺忘因子實時調整狀態的預測協方差陣,對過去的數據進行漸漸消除。其預測誤差方差陣:
(2)
式中:λk=diag(λk1∶λk2∶…∶λk18)。
實現自適應卡爾曼濾波的關鍵是如何實時在線確定遺忘因子λk1。
3.2 遺忘因子的計算[8~10]
最優遺忘因子λk1應滿足:
Pk/k-1HT-KkSK=0
(3)

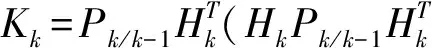
(4)
由Qk是半對稱正定陣,Rk和P0是正定對稱陣,Hk是非奇異陣:
(5)
得到:
(6)
將式(2)代入上式,得
(7)
設
設:λk1∶λk2∶…∶λk18=Ck(a1∶a2∶…∶a18)
式中:a1∶a2∶…∶a18可由系統先驗知識確定,對上式兩邊同時求跡得到Ck近似值為
(8)
引入調整系數a(a>1),人為加大λk,強制提高濾波器的跟蹤性能。得到的遺忘因子λk計算式:
λk=aCk(a1∶a2∶…∶a18)
(9)
4 仿真分析
假設載體航跡為勻速直線運動,速度為20Kn,航向為45°,航跡起始點為緯度30°,經度為113°。捷聯式慣性導航系統已經初始對準,初始速度誤差、初始位置誤差、初始姿態誤差為0值,陀螺常值漂移為0.01°/h,陀螺一階馬爾科夫過程漂移為0.01°/h,相關時間為600s,加速度計的一階馬爾科夫過程漂移為0.001m/s^2,相關時間為1000s;設航行過程中衛星導航系統位置誤差為20m,速度誤差為0.05m/s,數字電子羅盤的角度誤差為5′,卡爾曼濾波系統濾波周期為1s,系統仿真時間為2000s。
4.1 載體姿態誤差
圖2和圖3分別表示常規卡爾曼濾波姿態誤差估計和基于遺忘因子估計自適應卡爾曼濾波姿態誤差估計仿真圖。從圖中可以看出:基于遺忘因子估計的自適應濾波姿態誤差角沒有出現隨時間推移誤差累積的現象,也沒有出現濾波發散的現象。在仿真過程中誤差一直保持在較低水平,而且穩定性較常規卡爾曼濾波有較大提升。縱搖角誤差一直保持在0.5°范圍之內,橫搖角誤差一直保持在1.5°范圍之內,航行角誤差一直保持在0.5°范圍內。
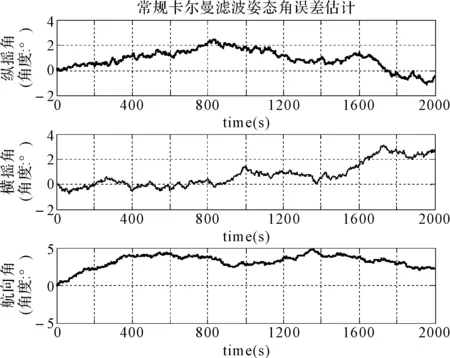
圖2 常規卡爾曼濾波姿態誤差估計仿真
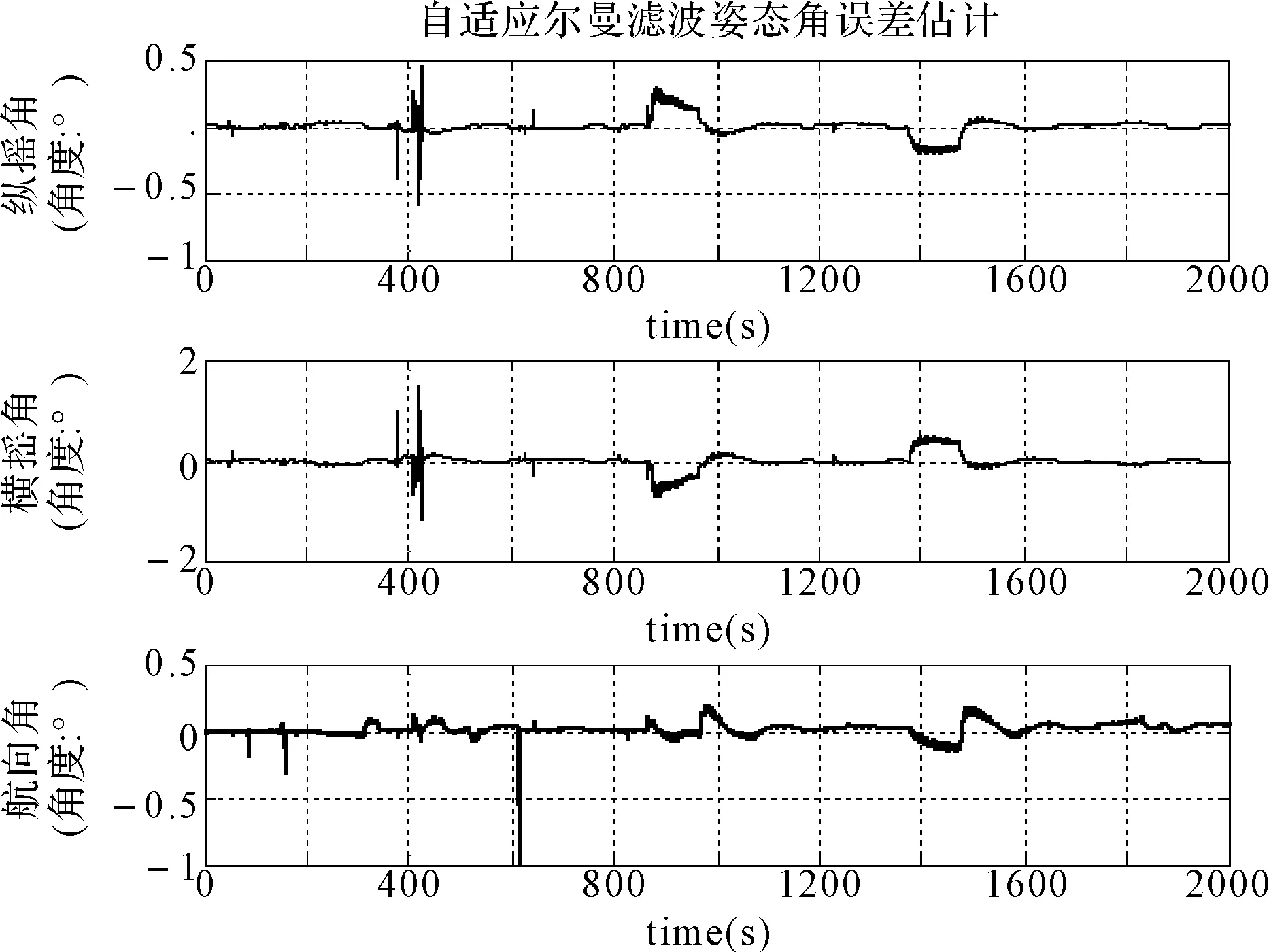
圖3 自適應卡爾曼濾波姿態誤差估計仿真
4.2 載體速度誤差
圖4和圖5分別表示常規卡爾曼濾波速度誤差估計和基于遺忘因子估計的自適應卡爾曼濾波速度誤差估計仿真圖。從圖中可以看出基于遺忘因子估計的自適應濾波速度誤差比較穩定,沒有出現隨時間推移誤差累積的現象,也沒有出現濾波發散的現象,一直保持在較低水平,而且穩定性較常規組合導航有較大提升。東向速度誤差一直保持在0.5m/s范圍之內,北向速度誤差一直保持在0.2m/s范圍之內,天向速度誤差一直保持在1.2m/s范圍內。
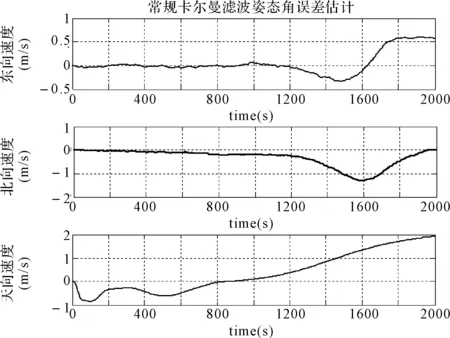
圖4 常規卡爾曼濾波航向誤差估計仿真

圖5 自適應卡爾曼濾波速度誤差估計仿真
4.3 載體位置誤差
圖6和圖7分別表示常規卡爾曼濾波位置誤差估計和基于遺忘因子估計的自適應卡爾曼濾波位置誤差估計仿真圖。從圖中可以看出基于遺忘因子估計的自適應濾波位置誤差沒有出現隨時間推移誤差累積的現象,也沒有出現濾波發散的現象。在仿真過程中誤差一直保持在穩定較低水平,緯度誤差保持在2m范圍內,經度誤差保持在5m范圍內,深度誤差保持在4m范圍內。
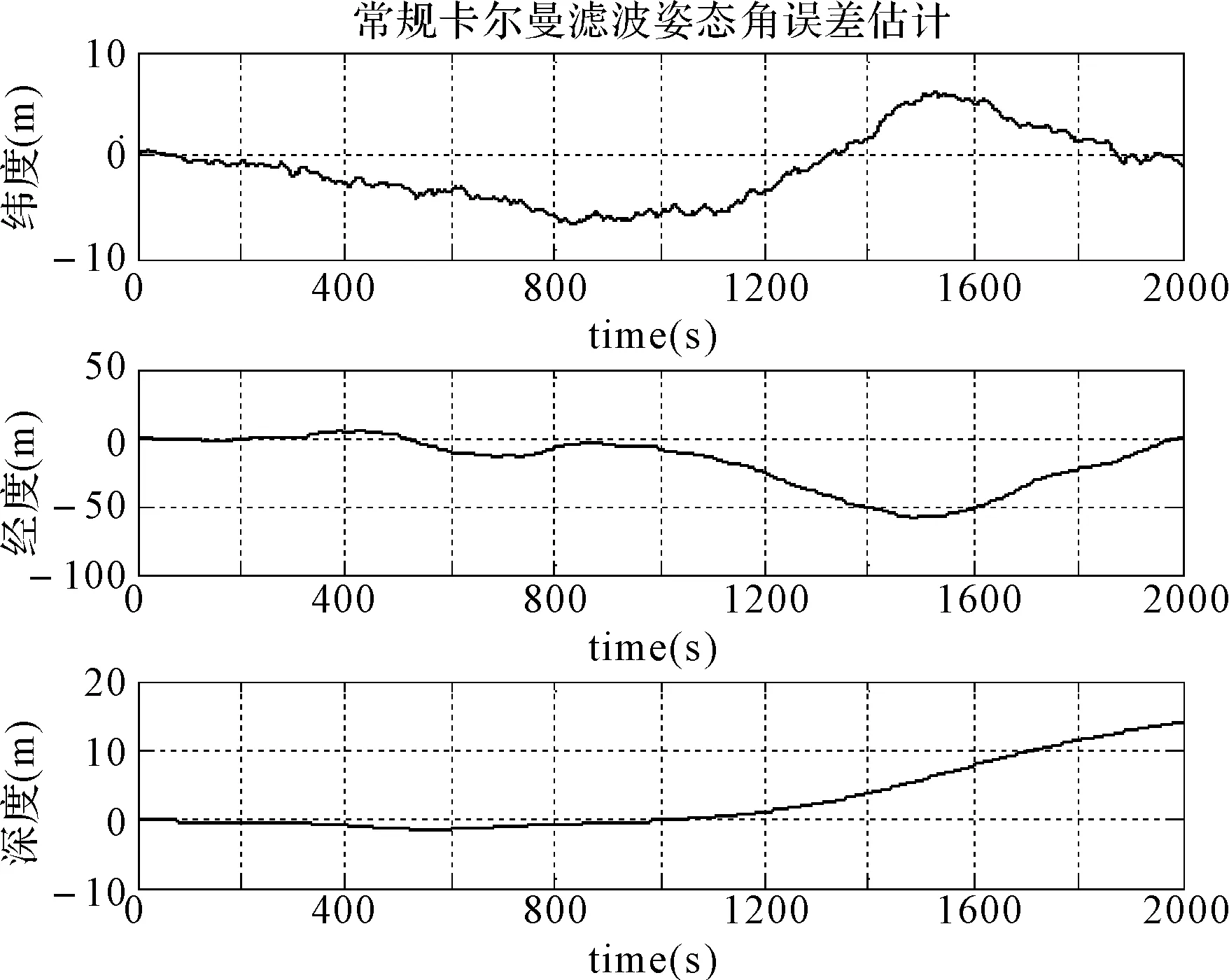
圖6 常規卡爾曼濾波位置誤差估計仿真
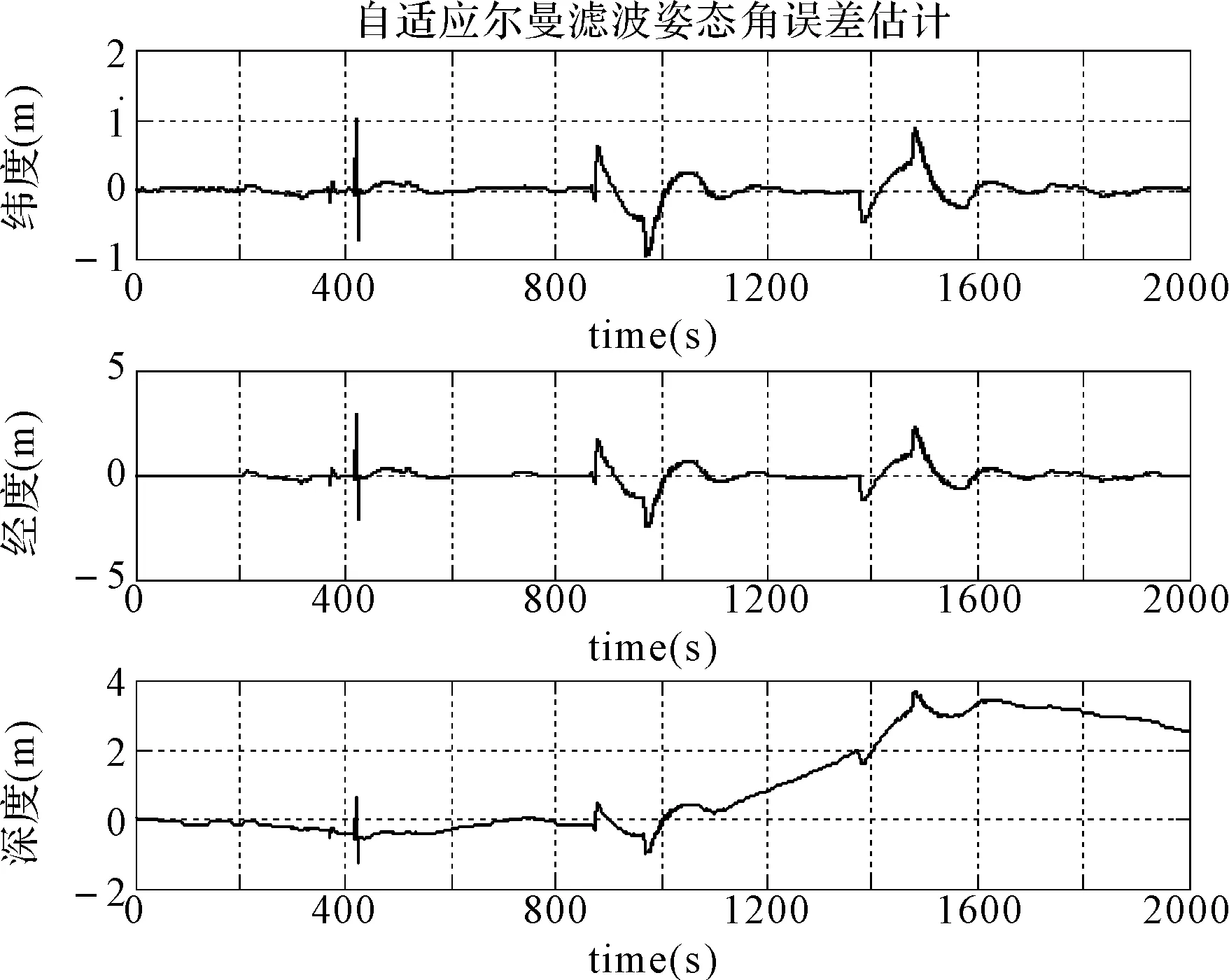
圖7 自適應卡爾曼濾波位置誤差估計仿真
基于遺忘因子的自適應卡爾曼濾波組合導航,通過引進遺忘因子自動調節目前時刻的濾波參數,增大最近時刻數據的權值,加大新近觀測數據的作用,減小過去時刻數據的權值,減小老舊觀測數據的影響,遺忘因子通過調整誤差方差陣P陣、濾波增益陣K陣和噪聲方差R陣地大小適應不同的偏差情況,從而解決濾波發散問題。從圖2~圖7可以看出,相對于常規卡爾曼濾波,帶有遺忘因子的自適應濾波對于濾波發散現象起到了明顯控制作用,體現出了較高的精度和較強的魯棒性。
5 結語
通過引進遺忘因子自動調節目前時刻的濾波參數,以適應信號和未知的噪聲隨時間變化的統計特性,加大新近觀測數據的作用,減小老舊觀測數據的影響。從仿真結果可以看出,濾波發散現象的得到了明顯控制,具有一定的魯棒性。
[1] 朱海,莫軍.水下導航信息融合技術[M].北京:國防工業出版社,2002:1-3.
[2] 田坦.水下定位與導航技術[M].北京:國防工業出版社,2007.
[3] 彭樹生.數字電子羅盤HMR3000的特性及應用[J].電子技術,2004(8):39-43.
[4] 蔣竅.MIMU/GPS/電子羅盤組合導航系統關鍵技術研究[D].太原:中北大學,2012.
[5] 卞鴻魏.艦艇組合導航系統自適應信息融合技術研究[D].上海:上海交通大學,2005.
[6] 卞鴻魏,李安.現代信息融合技術在組合導航中的應用[M].北京:國防工業出版社,2010.
[7] 張愛軍.水下潛器組合導航定位及數據融合技術研究[D].南京:南京理工大學,2009.
[8] Bian Hongwei, Jin Zhihua, Tian Weifeng. IAE-adaptive Kalman Filter for INS/GPS Integrated Navigation System[J]. Journal of Systems Engineering and Electronics,2006,17(3):502-508.
[9] 陳勇.信息融合技術在組合導航系統中的應用研究[D].南京:南京理工大學,2007.
[10] 徐冠雷,吉春生.自適應卡爾曼濾波法在潛艇水下導航中的應用[J].武器裝備自動化,2003,22(6):1-5.
Application of Forgetting Factor in SINS/GPS/BDS/EC Integrated Navigation Adaptive Filtering
ZHOU Kunfang YU Bo
(Naval Academy of Arms Command, Guangzhou 510430)
Aiming at the problem of conventional filter divergence, this paper advises to construct SINS/GPS/BDS/EC federal kalman filter and introduces adaptive filtering algorithm of forgetting factor so as to improve integrated navigation positioning precision. The simulation shows that the adaptive filtering with forgetting factor controls the filter divergence phenomena obviously relative to conventional filtering, embodies higher precision and strong robustness.
integrated navigation, adaptive filtering, forgetting factor
2015年3月8日,
2015年4月21日
周坤芳,男,教授,研究方向:導航定位技術。
U666.11
10.3969/j.issn.1672-9730.2015.09.014

