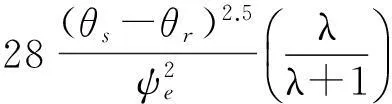Mualem模型中的飽和導水率修正研究
張 昊, 顧強康, 張仁義
(空軍工程大學 機場建筑工程系, 陜西 西安 710038)
?
Mualem模型中的飽和導水率修正研究
張 昊, 顧強康, 張仁義
(空軍工程大學 機場建筑工程系, 陜西 西安 710038)
摘要:[目的] 提高Mualem模型計算非飽和導水率的準確性。 [方法] 采用理論推導結合數據統計的方法研究該模型中的飽和導水率kspan修正問題。基于Brooks—Corey土壤水分特征曲線模型,建立修正導水率kspan與土壤水分特征曲線之間的理論關系式;通過回歸分析得到kspan與土壤水分特征曲線之間的理論關系式中相關參數。 [結果] 利用原狀黃土的非飽和滲透試驗數據,對考慮修正導水率kspan的Mualem模型的準確性進行了驗證,得到了比較滿意的結果。 [結論] 研究成果可用于依據土壤水分特征曲線直接確定非飽和土導水率,對非飽和導水率預測研究具有一定參考價值。
關鍵詞:非飽和土; 非飽和導水率; Mualem模型; 飽和導水率; 修正導水率; 土壤水分特征曲線
非飽和導水率是非飽和土研究中的一項重要內容。由于基質吸力的存在,不能用常規的測定飽和導水率的試驗方法來確定非飽和導水率,使得非飽和導水率的確定具有很大的難度[1]。通過土壤水分特征曲線來間接預測導水率的方法已得到廣泛認可。
Mualem非飽和導水率模型[2]因形式簡潔、適用性良好而被廣泛應用于非飽和導水率間接測定。飽和導水率ks是模型的重要參數,Mualem認為在非飽和滲流中,孔隙完全飽和時的導水率等于飽和滲流中的導水率。然而,飽和滲流與非飽和滲流的機理并不完全相同。van Genuchten[3]認為飽和導水率ks主要反映外力引起水在土孔隙中的流動特性,而非飽和滲流主要是由土體內部吸力引起的;Hoffmann—Riem[4]也認為Mualem需要通過修正來提高非飽和導水率的計算準確度;Marcel[4]通過對235組土樣分析,認為Mualem模型中飽和導水率ks應替換成修正導水率ko,并且ko比ks小一個數量級。
將飽和導水率ks用導水率ko來修正,可以提高Mualem模型的計算準確性。無法直接測定的修正導水率ko的取值則成為非飽和導水率間接測定研究中的重要問題。本文用理論推導結合數據統計的方法,探討 Mualem模型中的飽和導水率ks的修正問題,嘗試得到一個可以依據土壤水分特征曲線直接計算非飽和土導水率的Mualem修正模型。基于Brooks—Corey土壤水分特征曲線模型,首先建立修正導水率ko與土壤水分特征曲線之間的理論關系式,然后通過回歸分析求解相關參數,最后利用原狀黃土的非飽和滲透試驗數據對研究結果進行驗證。
1考慮修正導水率的Mualem模型
1.1修正導水率與土壤水分特征曲線之間關系的理論推導
非飽和導水率模型的計算式可寫成如下形式:
k=k0kr
(1)
在Mualem模型中,ko無法直接測量,是一個與孔隙半徑有關的參數。Mualem認為k0等于飽和導水率ks,而ks可通過試驗直接測定。然而在該模型中,k0是非飽和導水率曲線上的一點,其產生機理與飽和導水率ks并不完全相同。van Genuchten認為k0不等于ks的原因是二者的驅動力不同;Marcel通過數據分析認為ks比k0大一個數量級。所以需要對Mualem模型中的飽和導水率ks加以修正。
土的孔隙是一個互相連通的隨機系統,非飽和導水率表征水在孔隙的流動特性,Mualem方程、van Genuchten方程、Childs and Collis—George[5]方程都說明孔隙分布與非飽和導水率存在對應關系。Marshall[6],Toledo[7]和Xu[8]利用土體基于孔隙分形得出了相應的土壤水分特征曲線計算方程,說明土壤水分特征曲線能夠間接表征孔隙分布情況。土體孔隙的大小可通過孔隙半徑r表征。Mualem通過體積含水量定義孔隙的分布函數f(r):
(2)
則最小孔隙半徑為Rmin的土體中,孔隙半徑R以下的孔隙水的體積含水量可由f(r)的積分形式來表示,即:
(3)
式中:θr——殘余體積含水量(cm3/cm3);Rmin——孔隙半徑(m)。
當被水充滿的最大孔隙半徑等于土體最大孔隙半徑Rmax時,土體處于飽和狀態,即:
(4)
式中:θs——土體的飽和體積含水量(cm3/cm3)。
Yang—Lapalce在毛管模型中給出的半徑r與對應的吸力:
(5)
式中:Ts——水的表面張力(kg/m);α——接觸角(°)。
Brooks—Corey土壤水分特征曲線模型為:
(6)
式中:ψ——基質吸力(kPa);ψe——進氣值(kPa);λ——孔隙尺寸分布指標。
Mualem認為孔隙在三維空間上的體積分布與二維空間上的面積分布相同,即在面積分布密度函數為體積分布密度函數f(r)。在圖1所示的模型的基礎上建立了非飽和土導水率理論公式。
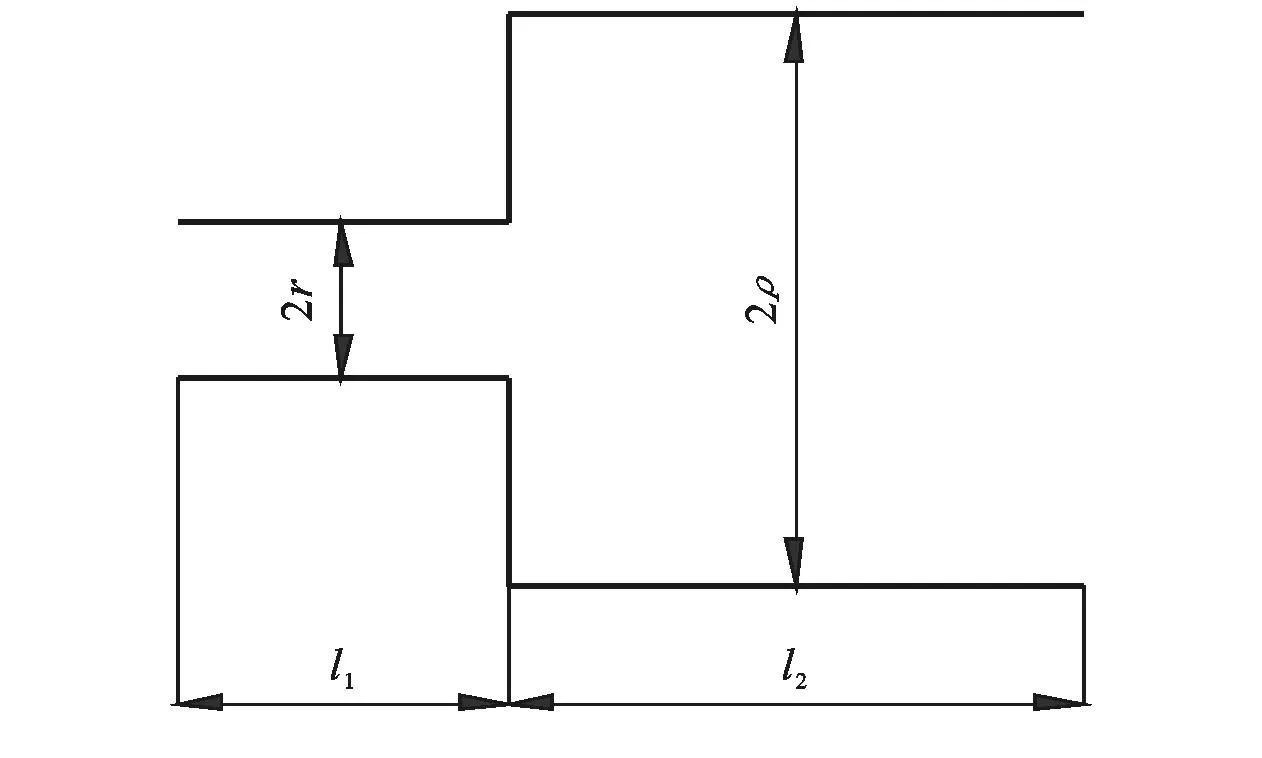
圖1 Mualem雙管聯通模型
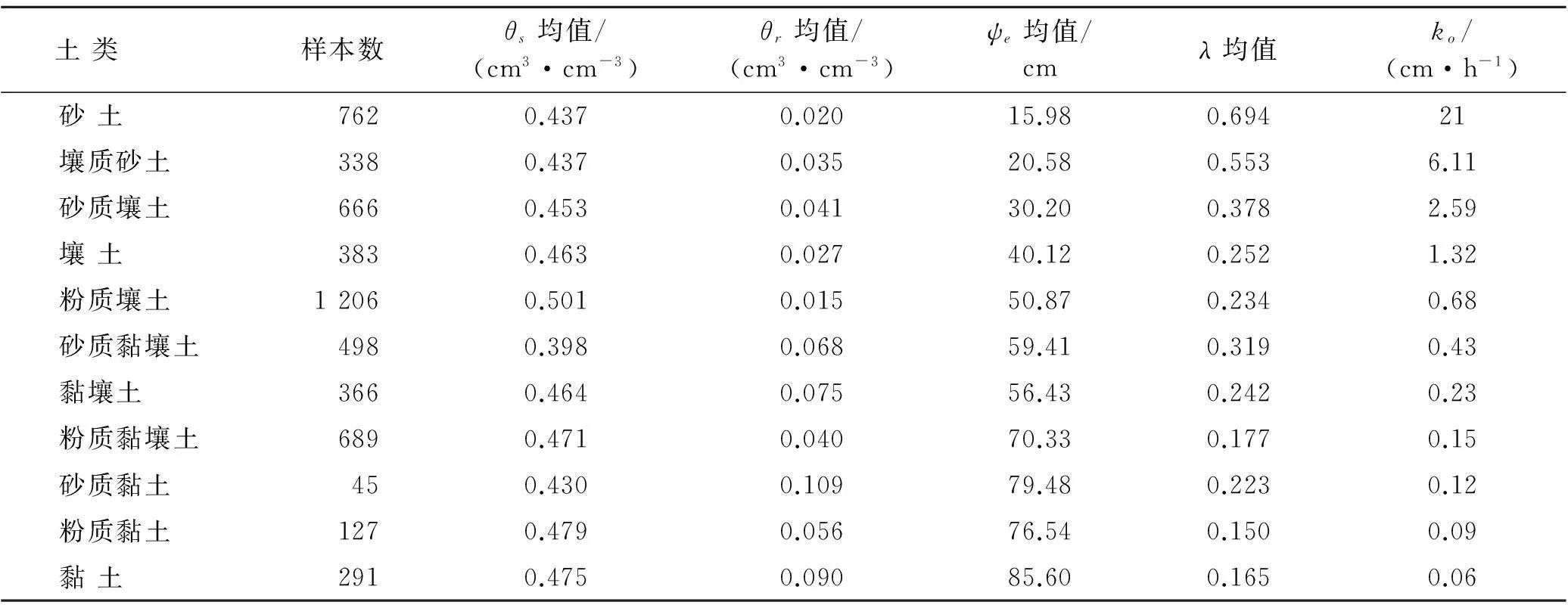
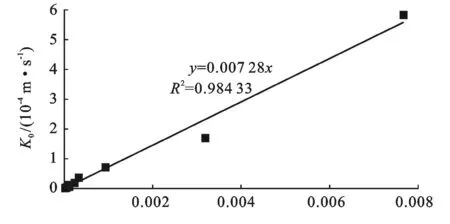
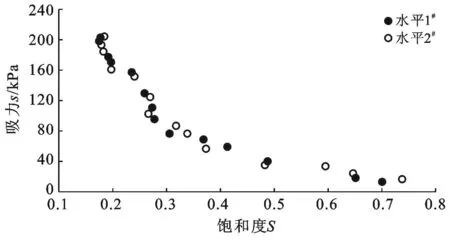
Mualem認為半徑r和半徑ρ孔隙聯通的概率為rρf(r)f(ρ)。因為rρf(r)f(ρ)沒有反映出水的滲流具有方向性,引入一個迂曲度因子T(0 (7) 將式(3)、式(5)和式(6)代入式(7),進行換元積分后有: (8) 故修正導水率k0為: (9) 參數M和T反映孔隙的形狀,目前還沒有有效的測試方法,Childs,Collis—George,Millington和Quirk[9],Burdine[10],Kunze[11]和Mualem都認為M與T的乘積與有效體積含水量呈冪指數關系,即: MT=B(θs-θr)l (10) 式中:B——常數。Childs和Collis—George認為l取0,Millington和Quirk認為l取4/3,Mualem認為l取0.5。將式(10)代入式(9),得: (11) 式中:A——常數,式(11)即為基于Brooks—Corey土壤水分特征曲線得到的修正導水率與土壤水分特征曲線理論關系。 常數A與孔隙形狀、重力加速度、水的表面張力、浸潤角、水的粘滯性有關。下面通過數據統計的方法對參數A的取值問題進行分析。Rawls依據粒徑組成將5 371組土細分成11類[12],統計出了各類土Brooks—Corey土壤水分特征曲線參數平均值,并根據非飽和導水率曲線給出了相應的修正導水率(原文標注為飽和導水率),結果如表1所示。常數A的擬合結果如圖2所示。將表1中的相關參數的單位換成常用單位,體積含水量的單位取cm3/cm3,進氣值的單位取kPa,導水率的單位取m/s。理論關系式中參數的統計求解結果如圖2所示。 表1 Rawls非飽和滲流參數統計結果 圖2 Rawls非飽和滲流常數A的擬合 由圖2可以看出,數據點分布在擬合直線附近,相關系數達到0.984。11類土的統計結果說明,修正導水率與土壤水分特征曲線參數之間呈現如式(11)所示的理論關系。擬合結果還說明,對不同的土類,式(11)中的參數A可以看成一個常數,其值可取0.007 28(m·kPa2)/s。 Mualem模型的修正導水率與土壤水分特征曲線參數之間的定量關系是: (12) 將Brooks—Corey土壤水分特征曲線模型帶入Mualem模型得到的相對導水率kr為: (13) 式中:δ——經驗常數,與孔隙尺寸分布指標λ有如下關系: (14) 將式(12)到(14)代入式(1),即得到考慮修正導水率k0的Mualem非飽和導水率模型: (15) 和原始模型比較,Mualem修正模型可以依據土壤水分特征曲線直接確定非飽和土導水率,并考慮了飽和導水率ks的修正。模型形式簡潔,參數較少,是一個確定非飽和土導水率的簡單方法。 2試驗驗證 姚志華[13]對蘭州和平鎮的原狀黃土的土壤水分特征曲線和非飽和導水率進行了測定。試驗采用2~3m之間的原狀黃土,平均干密度1.28g/cm3,平均含水量6.2%,顆粒的相對密度2.71,液限平均值為28.7%,塑限為17.6%(以上指標均為2~3m之間均值)。土壤水分特性曲線的測定結果如圖3。用Brooks—Corey模型對土壤水分特性曲線的結果進行擬合,結果如表2所示。本文用姚志華試驗得到的非飽和滲流參數試驗數據,對本文得出的Mualem修正模型進行檢驗。 利用式(15)計算得到的理論值與實測結果進行比較,結果示于圖4。 原文是通過擴散率與容水率計算得到非飽和導水率,在計算擴散率過程中,對實測體積含水率曲線進行平滑修正[14],導致修正段前后一定范圍內的導水率計算值偏離了真實值,修正段換算為飽和度正處于0.55到0.8區間內。圖4顯示在飽和度為0.8時非飽和導水率為2.10×10-5m/s,而姚志華實測得該土樣的飽和導水率為2.76×10-6m/s,前者比后者大一個數量級。從圖4可以看出,飽和度小于0.55段內,導水率理論曲線與試驗點吻合度高,認為本文對Muale-m模型的修正結果合理。 圖3 土壤水分特征曲線測定結果 θs/(cm3·cm-3)θr/(cm3·cm-3)ψe/kPaλR20.528011.470.5780.9943 圖4 修正Mualem模型的驗證 3結 論 飽和導水率ks影響Mualem模型計算準確性,用理論推導結合數據統計的方法對Mualem模型中的飽和導水率ks進行了修正。主要工作如下: (1) 將Mualem模型中的飽和導水率ks替換成修正導水率ko,基于Brooks—Corey土壤水分特征曲線模型,建立修正導水率ko與土壤水分特征曲線之間的理論關系式,用數據統計的方法求解理論關系式中的相關參數。得到一個可以通過土壤水分特征曲線直接確定非飽和土導水率的Mualem修正模型。 (2) 利用蘭州和平鎮的原狀黃土的非飽和滲流參數試驗數據對Mualem修正模型的準確性進行檢驗,試驗值與理論曲線吻合性高,取得很好的檢驗結果。 (3) 用于對本文得到的Mualem修正模型的檢驗數據較少,研究成果的普遍適用性還需要進一步的研究。 [參考文獻] [1]謝定義,陳正漢.非飽和土力學特性的理論與測試[C]∥土力學及基礎工程學會.非飽和土理論與實踐學術研討會文集.北京:北京科技出版社,1992:227-229. [2]Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976,12(3):513-522. [3]van Genuchten M T, Nielsen D R. On describing and predicting the hydraulic properties of unsaturated soils[J]. Ann. Geophys., 1985,3(5):615-628. [4]Schaap M G, Leij F J. Improved prediction of unsaturated hydraulic conductivity with the Mualem—van Genuchten model[J]. Soil Science Society of America Journal,2000,64(3):843-851. [5]Childs E C, Collis—George N. The permeability of porous materials[J]. Proceedings of the Royal Society of London(Series A): Mathematical and Physical Sciences, 1950,201,1066:392-405. [6]Marshall T J. A relation between permeability and size distribution of pores[J]. Journal of Soil Science, 1958,9(1): 1-8. [7]Toledo P G, Novy R A, Davis H T, et al. Hydraulic conductivity of porous media at low water content[J]. Soil Science Society of America Journal, 1990,54(3):673-679. [8]Xu Y. Calculation of unsaturated hydraulic conductivity using a fractal model for the pore-size distribution[J]. Computers and Geotechnics, 2004,31(7):549-557. [9]Millington R J, Quirk J P. Permeability of porous solids[J]. Trans. Faraday Soc., 1961,57:1200-1207. [10]Burdine N T. Relative permeability calculations from pore size distribution data[J]. Journal of Petroleum Technology, 1953,5(3):71-78. [11]Kunze R J, Uehara G, Graham K. Factors important in the calculation of hydraulic conductivity[J]. Soil Science Society of America Journal, 1968,32(6):760-765. [12]Rawls W J, Brakensiek D L. Prediction of soil water properties for hydrologic modeling[C]. ASCE, 1985. [13]姚志華,陳正漢,黃雪峰,等.非飽和原狀和重塑Q3黃土滲水特性研究[J].巖土工程學報,2012,34(6):1020-1027. [14]雷志棟,楊詩秀,謝森傳.土壤水動力學[M].北京:清華大學出版社,1988:21,92-94. Modification of Saturated Hydraulic Conductivity in Mualem Model ZHANG Hao, GU Qiangkang, ZHANG Renyi (DepartmentofAirportArchitecturalEngineering,AirForceEngineeringUniversity,Xi’an,Shaanxi710038,China) Abstract:[Objective] In order to improve the accuracy of saturated hydraulic conductivity in the Mualem model. [Methods] The modification of the saturated hydraulic conductivitykspanin the Mualem model was studied by theoretical method combined with data statistics. Based on the Brooks—Corey soil-water characteristic curve(SWCC) of unsaturated soil, a theoretical relationship between modified hydraulic conductivity and SWCC was presented, in which the correlation parameter was solved by regression analysis. [Results] Experimental data of undisturbed loess were used to evaluate the prediction outcomes of the Mualem model considering modified hydraulic conductivitykspan, which showed satisfactory result. [Conclusion] This theoretical model can be used to determine unsaturated hydraulic conductivity directly from SWCC, which possesses some references for further research on the prediction of unsaturated hydraulic conductivity. Keywords:unsaturated soils; unsaturated hydraulic conductivity; Mualem model; saturated hydraulic conductivity; modified hydraulic conductivity; soil-water characteristic curve 文獻標識碼:B 文章編號:1000-288X(2015)03-0168-04 中圖分類號:TU43 收稿日期:2014-11-12修回日期:2014-12-02 資助項目:省部級項目“陜西延安機場工程” 第一作者:張昊(1991—),男(漢族),江蘇省南京市人,碩士研究生,研究方向為地基處理與邊坡穩定。E-mail:fourapril@sina.cn。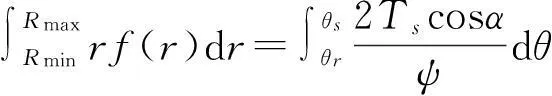

1.2 參數A的統計求解