一類帶有函數指數的Logistic方程正解的有界性

冀鐵果，趙雪婷，董 衛

(1.河北工程大學 理學院，河北邯鄲056038;2.河北工程大學水電學院，邯鄲056038)

我們將討論方程

正解的有界性，其中λ(x)和a(x)是RN中正的連續函數，且存在正常數λ∞和β使得是連續函數且存在常數，使得

方程(1)揭示了空間異質性對化學反應影響的模型。對p＞1是正常數的情形，此類問題被廣泛研究，詳見參考文獻［1－4］。我們綜合利用文獻［2］中的Sliding Method以及文獻［3］中的比較原理，得到了方程(1)正解的有界性。

結論及證明

定理:存在正常數L＞1，使方程(1)的所有正解μ，都有μ≤L。當|x|→∞ 時，所有正解μ滿足:

本定理的證明分解為引理1和引理2的證明。

引理1:如果μ是方程(1)的正解，則

設γ:}表示一條連續曲線，并且滿足

取常數L＞ max{1，supRnμ}，使，則有

對任意小的正數ε＞0，總可在內找到足夠大的正數R=Rε＞0使得不等式+ε和p∞－ε＜p(x)＜p∞+ε同時成立。由于 sup|x|=Rv＜1，所以可在區間(sup|x|=Rv，1)內選一個常數η，做方程

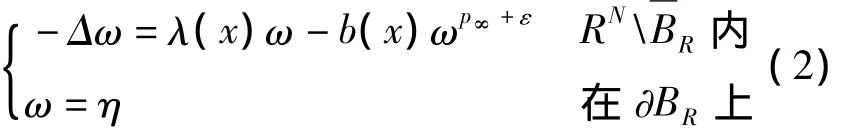
令wε表示方程(2)的唯一正解。根據文獻［3］中的定理 1 可知，當 |x|→∞ 時，ωε→，即

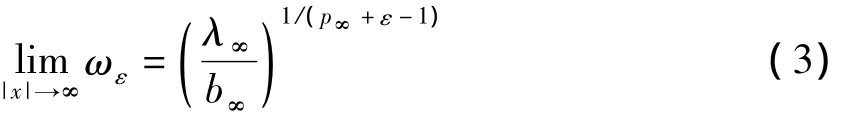
可以取足夠小的正數ε，使不等式 0＜成立。

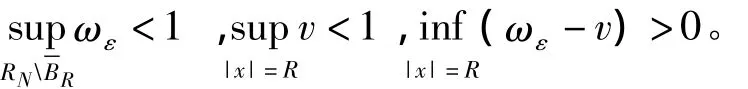
假設k*＞1，則函數是C2上的非負函數且在上滿足:

當k*≤1時，由于ωε≥v，且，所以μ=Lv≤Lωε。由式(3)可得

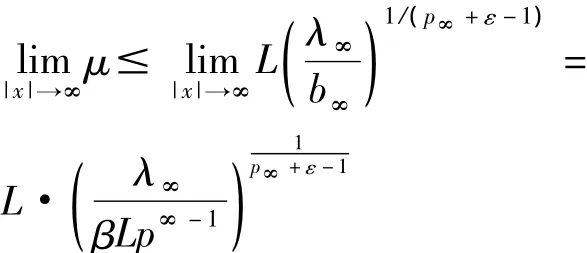
所以

［1］HENRI BERESTYCKI，FRANCOIS HAMEL，LUCA ROSSI.Liouville－ type results for semilinear elliptic equations in unbounded domains.Ann.Mat.Pura Appl.(4)，2007(3):469－507.

［2］WEI DONG.Positive solutions for logistic type quasilinear elliptic equations on RN .［J］.Math.Anal.Appl.，2004(2):469－480.

［3］YIHONG DU，LI MA.Logistic type equations on RN by a squeezing method involving boundary blow－up solutions［J］.London Math.Soc.2001，64(1):107 －124.

［4］YIHONG DU，LI MA.Positive solutions of an elliptic partial differential equation on RN［J］.Math.Anal.Appl.，2002(2):409 －425.