雙曲余弦高斯光束在非Kolmogorov湍流中的湍流距離

湯明玥，李賓中

(川北醫(yī)學(xué)院基礎(chǔ)醫(yī)學(xué)院，南充637000)

引 言

在激光理論中，湍流距離是用來定量描述湍流對(duì)光束擴(kuò)展影響的物理量，定義為由于湍流導(dǎo)致光束橫截面積擴(kuò)展達(dá)湍流中該處橫截面積10%時(shí)的距離。近年來，國(guó)內(nèi)外科研工作者們利用湍流距離定量地研究了湍流對(duì)激光束擴(kuò)展的影響［1-5］。2009年，ZHONG等人研究了環(huán)狀光束在湍流中的擴(kuò)展，并發(fā)現(xiàn)湍流距離隨光束遮攔比ε的增大而增大，即ε越大湍流對(duì)光束擴(kuò)展的影響就越小［4］。2011年，LIU等人求解出部分相干雙曲余弦高斯列陣光束的湍流距離的半解析表達(dá)式，并研究了湍流距離隨光束參量、湍流強(qiáng)度及光束疊加方式的變化情況［5］。然而，這些研究都是針對(duì)理想大氣湍流，如常規(guī)Kolmogorov湍流，但近來實(shí)驗(yàn)測(cè)量結(jié)果與理想的Kolmogorov湍流模型有較大的偏差［6］。TOSELLI等人［7］通過引入湍流廣義指數(shù)和廣義振幅因子來描述非Kolmogorov湍流模型，所得理論研究結(jié)果與實(shí)驗(yàn)數(shù)據(jù)更為接近。基于該模型，國(guó)內(nèi)外學(xué)者于近期對(duì)激光束在非Kolmogorov湍流中的傳輸特性開展了一些相關(guān)的研究［8-12］。

另一方面，余弦高斯光束是厄米正弦類高斯光束的一種特例，厄米正弦類高斯光束是傍軸近似下波動(dòng)方程的新解，它代表了一大類光束［13-14］。余弦高斯光束是在傳輸過程中不能保持其形狀不變的一類光束，選取一定的偏心參量能使其在空間某處得到近平頂分布的光束。1999年，WANG等人指出新型的CO2激光器的諧振腔具有特殊的機(jī)構(gòu)，即在其中一塊反射鏡上帶有相位臺(tái)階，從而提出余弦高斯光束［15］。基于余弦高斯光束在優(yōu)化激光放大器的效率方面有一定實(shí)際應(yīng)用價(jià)值，國(guó)內(nèi)外科研工作者對(duì)此類光束展開了大量研究。

作者選用部分相干雙曲余弦高斯光束作為激光模型，推導(dǎo)出了部分相干雙曲余弦高斯光束在非Kolmogorov湍流中的湍流距離解析表達(dá)式，并研究了湍流參量和光束參量對(duì)湍流距離的影響，得到一些了有意義的結(jié)果。

1 理論模型

以部分相干雙曲余弦高斯光束為理論模型，其在z=0處的交叉譜密度函數(shù)表示為［16］:

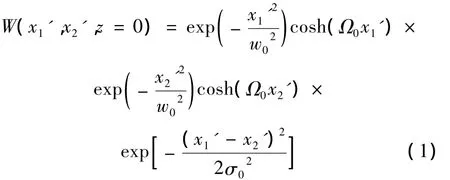
式中，w0和σ0分別為z=0處光束的束腰及相干長(zhǎng)度，Ω0是與雙曲余弦有關(guān)的光束參量［14］，x1′，x2′指z=0平面處，x軸坐標(biāo)中的兩點(diǎn)位置。

基于廣義惠更斯-菲涅耳原理，光束通過湍流傳輸?shù)钠骄鈴?qiáng)表示為［17］:

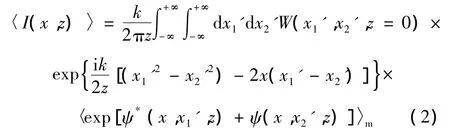
式中，x指z≠0時(shí)x軸某點(diǎn)位置，λ為波長(zhǎng)，k是波數(shù)(k=2π/λ)，ψ(x，x′)表示湍流介質(zhì)特性決定的復(fù)相位函數(shù)，* 是共軛，〈〉m是系綜平均，且其中，J0為0 階 Bessel函數(shù)，Φ(κ，α)為湍流介質(zhì)的折射率起伏空間譜密度函數(shù)。κ，α，ξ分別表示空間頻率、湍流廣義指數(shù)和傳輸路徑參量。湍流模型采用非Kolmogorov統(tǒng)計(jì)，則Φ(κ，α)可表示為［7］:

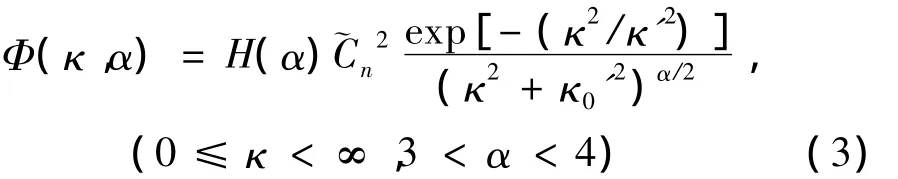
式中，l0和 L0分別為湍流的內(nèi)尺度及外尺度，κ′=c(α)/l0，κ0=2π/L0，~Cn2為廣義折射率結(jié)構(gòu)函數(shù)(單位為m3-α)。另外，H(α)和 c(α)的表達(dá)式由參考文獻(xiàn)［7］中給出。若 α =11/3，H(11/3)=0．033，C~n2=Cn

2，即簡(jiǎn)化為常規(guī) Kolmogorov 功率譜［7］。

根據(jù)二階矩束寬的定義［1］，并引入新的變量u=(x1′+x2′)/2，v=x1′-x2′。經(jīng)過復(fù)雜的積分運(yùn)算可得部分相干雙曲余弦高斯光束在非Kolmogorov湍流中的二階矩束寬為:

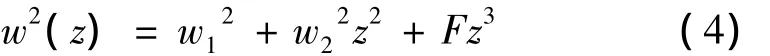
其中:

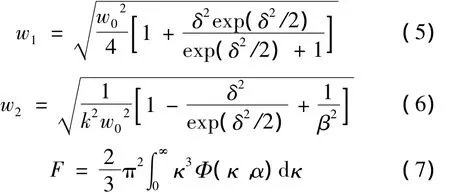
式中，β=σ0/w0為光束相干參量，δ=Ω0w0為光束離心參量［15］。

若F=0，(4)式化簡(jiǎn)為部分相干雙曲余弦高斯光束在自由空間中的二階矩束寬:

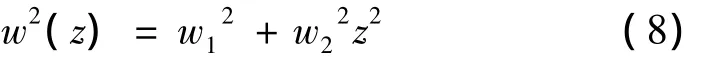
(4)式的前兩項(xiàng)表示部分相干雙曲余弦高斯光束通過自由空間傳輸?shù)亩A矩束寬，它與光束參量(w0，λ，β，δ)相關(guān);第3項(xiàng)為湍流導(dǎo)致的光束擴(kuò)展，結(jié)合(3)式可知，其與湍流廣義指數(shù)α、內(nèi)尺度l0及外尺度L0相關(guān)。

湍流距離zt指光束擴(kuò)展開始明顯受到湍流影響的傳輸距離，是定量描述湍流對(duì)光束擴(kuò)展影響的物理量，其定義為湍流導(dǎo)致光束擴(kuò)展達(dá)10%的距離［1］，將(4)式和(8)式代入，得zt滿足三次方程，即:

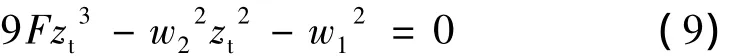
求解上式，zt有唯一實(shí)解，即:

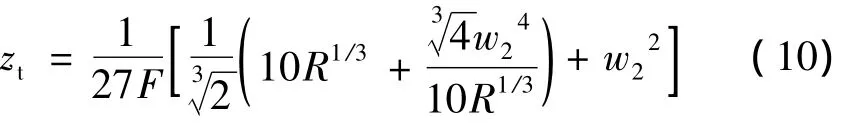
其中，

(10)式為部分相干雙曲余弦高斯光束傳輸于非Kolmogorov湍流的湍流距離zt解析式，光束參量(w0，λ，β，δ)與湍流參量(α，L0，l0)對(duì) zt有一定影響。顯然，zt表征湍流對(duì)光束擴(kuò)展的影響，即zt越小，光束擴(kuò)展受湍流的影響則越大。

2 數(shù)值計(jì)算與分析

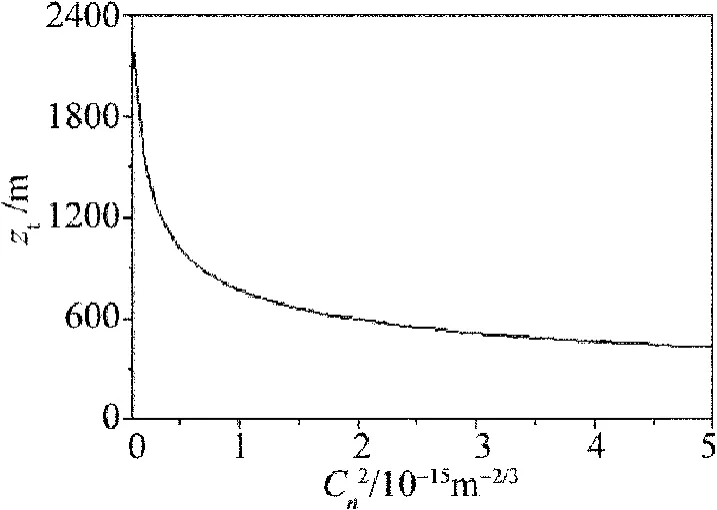
Fig.1 ztversus Cn2

圖1 中給出了常規(guī)Kolmogorov湍流中湍流距離zt隨折射率結(jié)構(gòu)常數(shù)Cn2的變化，其中計(jì)算參量λ=1.06μm，α =11/3，w0=0.05m，β =0．1，δ=2，L0=20m，l0=0.01m。

圖2和圖3為湍流距離zt對(duì)不同內(nèi)尺度l0、外尺度L0隨湍流廣義指數(shù)α的變化情況，計(jì)算參量~Cn2=2×10-15m3-α，其余計(jì)算參量與圖1一致。

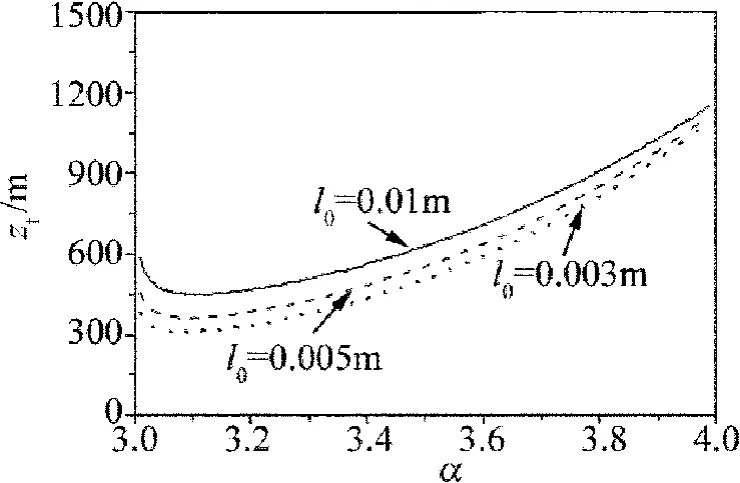
Fig.2 ztversus α for different values of l0

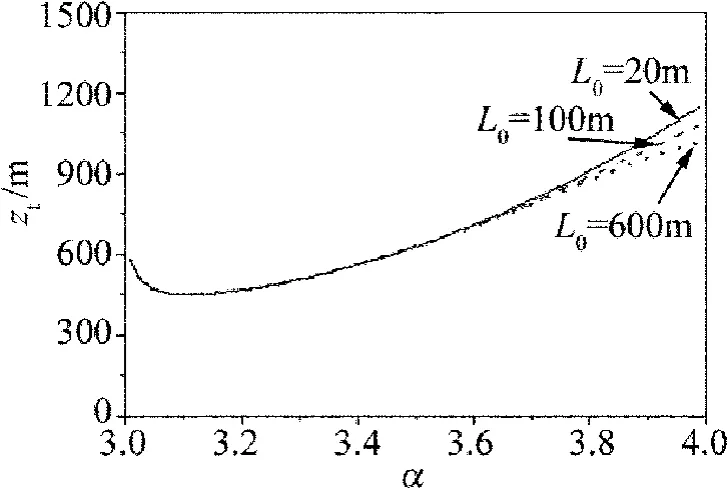
Fig.3 ztversus α for different values of L0

由圖2可知，zt隨著Cn2的增大而減小，即湍流的增強(qiáng)使得湍流距離縮短，這也可從(10)式得到該結(jié)論。圖2顯示zt隨α的增大而先減小后增大，且在α=3．11處時(shí)存在極小值，其物理原因:在(7)式中湍流項(xiàng)F是一個(gè)有關(guān)α的函數(shù)，F(xiàn)隨α增大而先增大后減小，且在α=3．11處時(shí)取最大值，極大的湍流值將導(dǎo)致極小的湍流距離。另外，圖2還說明，zt隨l0的增大而增大，當(dāng)α＞3．11時(shí)，隨著α的增大，各條曲線之間的差別在逐漸縮小，即廣義指數(shù)α越大，內(nèi)尺度l0對(duì)于湍流距離的影響越小。

圖3顯示，當(dāng)0＜α＜3．6時(shí)，各條曲線之間無差別;而當(dāng)3．6＜α＜4時(shí)，zt隨L0的增大而減小。

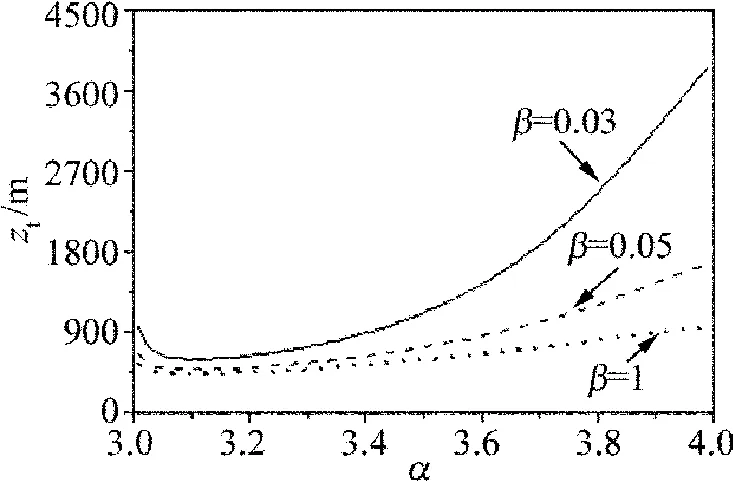
Fig.4 ztversus α for different values of β

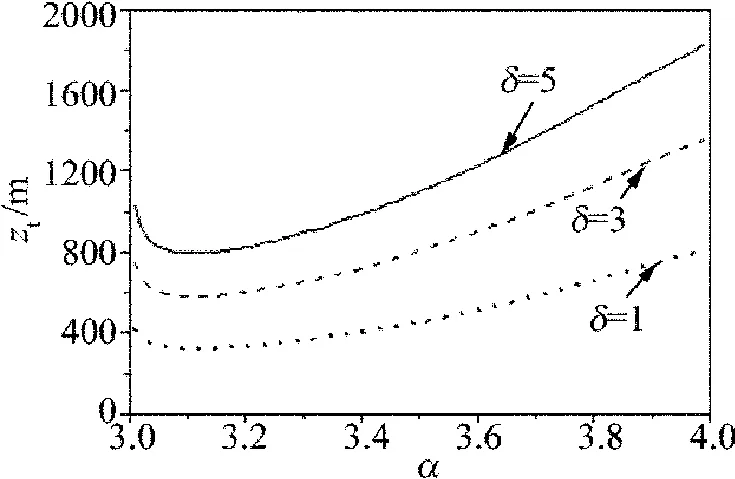
Fig.5 ztversus α for different values of δ

圖4 、圖5為湍流距離zt對(duì)不同光束參量(光束相干參量β、光束離心參量δ)隨湍流廣義指數(shù)α的變化情況。

由圖4可以看出，zt隨β的增加而逐漸減小，即相干性越差的光束湍流距離越大，光束受湍流的影響則越小;而當(dāng)β取值較大(β=1)時(shí)，湍流距離zt隨α的變化則不明顯。

圖5指出，zt隨光束δ的增大而增大，即離心參量越大，湍流距離越大，光束擴(kuò)展受湍流的影響越小。這與常規(guī)Kolmogorov湍流中的研究結(jié)果是一致的。

3 結(jié)論

基于廣義惠更斯-菲涅耳原理，并采用非Kolmogorov湍流模型，推導(dǎo)出了部分相干雙曲余弦高斯光束在非Kolmogorov湍流中的湍流距離，研究了湍流參量與光束參量對(duì)湍流距離的影響。研究發(fā)現(xiàn):在常規(guī)Kolmogorov湍流中，湍流距離zt隨著折射率結(jié)構(gòu)常數(shù)Cn

2的增大而減小，即湍流的增強(qiáng)使得湍流距離縮短;在非Kolmogorov湍流中，湍流距離zt隨湍流廣義指數(shù)α的變化表現(xiàn)出非單調(diào)性，zt隨α的增大而先減小后增大，且當(dāng)α=3．11時(shí)存在極小值，即此刻湍流對(duì)光束擴(kuò)展的影響最大。湍流距離zt隨內(nèi)尺度l0的增大而增大，且當(dāng)α＞3．11時(shí)，α越大，l0對(duì)于zt的影響越小;zt隨外尺度L0的增大而減小(僅當(dāng)3．6＜α＜4時(shí))，而在0＜α＜3．6時(shí)，L0的變化對(duì)湍流距離zt無影響。光束相干參量β越小和光束離心參量δ越大，湍流距離zt則越大，即β越小、δ越大，光束擴(kuò)展受湍流的影響就越小。

本文中所得理論結(jié)果對(duì)部分相干雙曲余弦高斯光束在湍流中擴(kuò)展、方向性的控制及相關(guān)應(yīng)用有實(shí)際意義。

［1］ GBUR G，WOLF E.Spreading of partially coherent beams in random media［J］.Journal of the Optical Society of America，2002，A19(8):1592-1598.

［2］ ZHU Zh W，SU Zh P.Spectral change of J0-correlated partially coherent flat-topped beam in turbulent atmosphere［J］.Laser Technology，2012，36(4):532-535(in Chinese).

［3］ JI X L，ZHANG E T，Lü B D.Spreading of partially coherent flattened Gaussian beams propagating through turbulent media［J］.Journal of Modern Optics，2006，53(12):1753-1763.

［4］ ZHONG Y L，CUI Zh F，SHI J P，et al.Propagation properties of partially coherent flat-topped beam array in a turbulent atmosphere［J］.Laser Technology，2010，34(4):542-546(in Chinese).

［5］ LIU F，JI X L.Turbulence distance of partially coherent cos-Gaussian array beams［J］.Chinese Journal of Lasers，2011，38(7):0713001(in Chinese).

［6］ RAO C H，JIANG W H，LING N.Spatial and temporal characterization of phase fluctuations in non-Kolmogorov turbulence［J］.Journal of Modern Optics，2000，47(6):1111-1126.

［7］ TOSELLI I，ANDREWS L C，PHILLIPS R L，et al.Free space optical system performance for laser beam propagation through non Kolmogorov turbulence for uplink and downlink paths［J］.Proceedings of the SPIE，2007，6708:670803.

［8］ WU G H，GUO H，YU S，et al.Spreading and direction of Gaussian-

Schell model beam through a non-Kolmogorov turbulence ［J］.Optics Letters，2010，35(5):715-717.

［9］ XU H F，CUI Z F，QU J.Propagation of elegant Laguerre-Gaussian beam in non-Kolmogorov turbulence［J］.Optics Express，2011，19(22):21163-21173.

［10］ HE X M，Lü B D.Propagation properties of partially coherent Hermite-Gaussian beams through non-Kolmogorov turbulence［J］.Chinese Physics，2011，B20(9):094210.

［11］ DENG J P，JI X L，LU L.Propagation of polychromatic partially coherent decentred laser beams propagating in non-Kolmogorov turbulence［J］.Acta Physica Sinica，2013，62(14):144211(in Chinese).

［12］ HUANG Y P，ZENG A P.Propagation properties of Hermite-Gaussian beams in non-Kolmogorov turbulence［J］.Acta Photonica Sinica，2012，41(7):818-823(in Chinese).

［13］ LIU L，HAO Zh Q.Propagation of sinh-Gaussian beams in gradientindex medium［J］.Laser Technology，2013，37(1):126-129(in Chinese).

［14］ LI P，KUANG A H.Propagation characteristics of non-paraxial partially coherent Hermite-cosine-Gaussian beams［J］.Laser Technology，2014，38(1):141-144(in Chinese).

［15］ WANG Sh M，LIN Q，JIANG X Q.Cosine-Gauss beam［J］.Acta Photonica Sinica，1999，28(4):367-390(in Chinese).

［16］ JI X L.Influence of turbulence on the Rayleigh range of partially coherent cosh-Gaussian beams［J］.Acta Physica Sinica，2011，60(6):064207(in Chinese).

［17］ ANDREWS L C，PHILLIPS R L.Lazer beam propagation through random media［M］.Washington DC，USA:SPIE Press，1998:17-29.