基于反射強度和K-means聚類的平面標靶定位研究

吳 超，袁永博，張明媛

(大連理工大學建設工程學部，大連116024)

引 言

3維激光掃描技術能夠快速獲取復雜環境和空間目標的3維立體信息。在掃描過程中，要想獲得被測目標的完整空間數據，需從不同視角對被測物體進行掃描。由于不同測站的掃描數據間坐標關系未知，所以需要進行點云數據的拼接配準將各個位置的掃描數據統一到一個坐標系下。另外，在某些應用中需要實現掃描坐標系與大地坐標系之間的轉換。在處理這些問題時，公共點轉換法是一種常用的方法。在進行公共點掃描定位的時候，由于難以從點云數據中精確提取點狀特征，這就造成在確定公共點掃描坐標的時候存在著定位誤差，進而使得基于公共點轉換的算法精度會受到影響［1］。在高精度測量中，需要配合特定形狀的標靶進行特征點輔助定位［2］。輔助標靶一般有平面標靶和球狀標靶兩種，由于球狀標靶無法一次獲取全部表面數據，所以本文中討論平面靶標的坐標定位問題。

目前，對于平面標靶的中心坐標識別大多采用人機交互的方式，在后期處理軟件中手動或自動提取中心坐標。如果采用軟件自動提取，需結合為掃描儀配備的專用平面標靶且在一定傾角范圍內使用［2］。在自動識別算法方面，LICHTI等人基于標靶中心掃描點反射強度最大的假設提出3種自動識別方法(maxrad，maxrad4，radcent)［3］，但是由于粗差點和掃描噪聲等因素的存在，使得最大反射強度的位置通常不在標靶的實際中心位置。VALANIS等人［4］提出了使用模糊C-means聚類算法的自動識別方法(fuzzypos)，并介紹了其它3 種識別方法(fuzzyposfine，gridrad，fuzzygridrad)，通過與LICHTI方法的比較驗證了其算法的準確性和可靠性。ZHOU等人［5］用中心投影原理將點云數據投影為2維影像，結合區域生長算法擬合出標靶中心的坐標。WANG等人［6］利用獲取的點云數據的反射強度，采用反射強度加權法識別平面標靶中心坐標。CHEN等人［7］采用重心類和幾何類方法獲得平面標靶坐標，并對其精度進行了分析比較，表明使用重心類方法可以獲得較高的平面標靶中心坐標精度。本文中利用獲取點云數據的反射強度值進行區域分割，對分割得到的每一區域基于K-means聚類方法得出區域中心坐標，進而獲得平面標靶的中心坐標。通過與重心法、反射強度加權法和軟件自動提取方法的結果比較，驗證本文中算法的準確性。

1 基于反射強度和K-means聚類的標靶中心自動識別算法

在對平面標靶定位之前，需要將標靶數據從掃描點云數據中分割出來，然后采用一定的算法將數據中的粗差點剔除。本文中采用人工選擇的方式得到平面標靶點云數據，在此基礎上利用總體最小二乘法消除數據中的異常值，將處理后的點云數據按照其反射強度值進行區域分割，利用K-means算法對每一區域數據進行聚類得到各區域聚類中心，然后采用均值化處理得到平面標靶中心。

1．1 粗差點剔除

由于各種因素影響(儀器本身、人為操作、外界環境、目標材質等)，掃描點云數據中難以避免會含有粗差點，使得原本規則的標靶數據存在異常，因此在進行識別前，需要對粗差點進行剔除。其具體步驟如下。

(1)對于空間平面方程z=ax+by+c，考慮數據在x，y，z 3個方向同時含有誤差的情況下［8］，平面方程變為 z+vz=a(x+vx)+b(y+vy)+c，其中 vx，vy，vz為 3個方向的誤差改正數。由于最小二乘法僅考慮因變量z含有誤差的情況下解算平面參量，因此采用總體最小二乘法［9］對掃描數據進行空間平面擬合，得出平面參量 a，b，c。

(2)根據下式計算每個掃描點到擬合平面的距離:

(3)根據(3)式計算掃描點到擬合平面距離的中誤差σ。以2倍中誤差作為閾值，如果＞2σ，視此點為粗差點，予以剔除。

1．2 基于反射強度的區域分割

掃描得到的點云數據一般包含空間坐標、反射強度以及顏色信息，其反射強度受掃描距離、掃描角度、目標材質及傳播介質等因素影響。對于常見的平面標靶來說，由于不同顏色區域激光反射強度值不同［10］，因此可以根據點云數據的反射強度值對標靶數據進行區域分割。考慮粗差處理后的點云數量確定最佳區域分割數目，然后按照反射強度值予以分級，使各區域點云數目相當，實現點云數據的區域分割。

1．3 K-means聚類和中心坐標提取

K-means算法是一種典型的基于劃分的聚類方法，目的在于把集中的數據劃分為一系列有意義的子集(或稱類)，使得每個子集中的數據盡量“相似”或“接近”，而子集與子集間的數據盡可能有“很大差異”。其原理是:對于含有n個數據點的集合X=(x1，x2，x3，…，xn)先取 k個初始聚類中心，計算每個樣本到聚類中心的距離，將樣本向距離最近的聚類中心歸類。所有樣品歸類完畢后，將各類中所有樣品的平均值作為新聚類中心，再重復上述過程直到聚類中心不再變化為止。

在對掃描數據分割為n個區域之后，對每一區域的點云選取k個初始聚類中心進行K-means聚類，得到每一區域的k個聚類中心點xi(i=1，2，…，k)，根據下式得到區域的中心點:

然后根據下式得到標靶中心點坐標p:

2 實驗分析

Fig.1 Common planer targets T1and T2

本文中采用Faro Focus 3-D激光掃描儀在實際應用過程中對兩種常見平面標靶(T1，T2)(如圖1所示)進行了掃描，兩次掃描的距離、角度和精度都不相同。在Faro Scene軟件中手動獲取平面標靶掃描原始點云后，利用基于奇異值分解［11］的總體最小二乘法擬合空間平面，將到擬合平面距離大于2倍中誤差的點剔除。重復剔除過程直到所有的點滿足≤2σ。最終處理結果見表1。

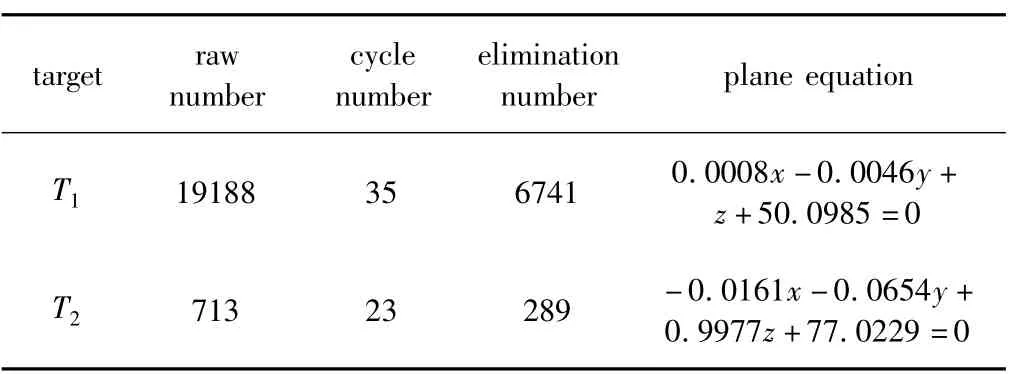
Table 1 Elimination results of noise points using the total least square algorithm

考慮點云數目，將處理之后的數據按照反射強度值進行合理區域分割。由于平面標靶為對稱形狀，分割之后每一區域的點云數據也大致對稱，因此對每一區域數據選擇k=2進行K-means聚類后，求得各區域中心坐標，然后采用均值化處理獲取各標靶的中心坐標。算法通過MATLAB R2010a軟件編程實現［12］。通過幾種不同識別方法的比較可以看出(如表2所示)，本文中采用的算法與軟件自動提取的坐標相差很小，在x，y，z不同方向上最大的坐標相差也在亞毫米級。

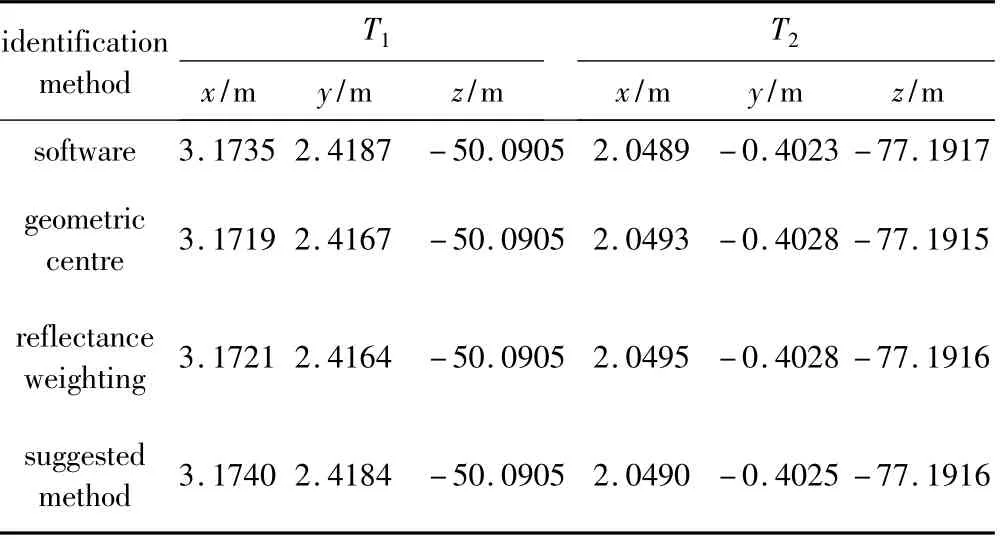
Table 2 Several methods for calculating the target center

另外，在軟件無法自動識別的情況下，采用本文中的算法對平面標靶進行識別，分別在10m和25m的掃描距離下自動識別兩個標靶的中心坐標，將計算得出的標靶之間距離與蘇一光RTS-112SL全站儀和其它兩種方法計算距離做比較(對比結果見表3)，在一定掃描距離內可以看出本文中的方法在實際應用時的有效性與準確性。

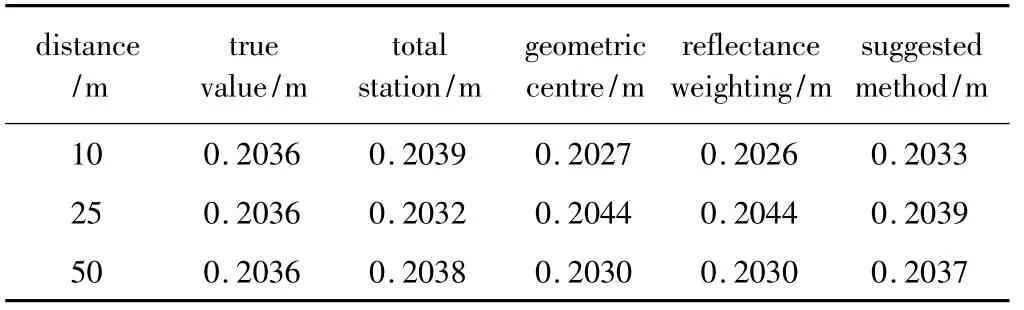
Table 3 Comparison of distance calculated with different methods

3 結論

通過與軟件自動提取及其它識別方法的比較表明，該算法獲得的結果與軟件自動提取結果相差精度在亞毫米級。同時，在一定距離內，當軟件無法自動提取時，該算法同樣可以得到較高的識別精度。在需要較高掃描精度的實際工程中，該算法具有較好的適用性。

［1］ WANG Y B，YANG H Ch，LIU Y H，et al.Linear-feature-constrained registration of LiDAR point cloud via quaternion［J］.Geomatics and Information Science of Wuhan University，2013，38(9):1057-1062(in Chinese).

［2］ ZHU L.Research on the target in TLS［J］.Laser Journal，2008，29(1):33-35(in Chinese).

［3］ LICHTI D D，STEWART M P，TSAKIRI M，et al.Benchmark tests on a three-dimensional laser scanning system［J］.Geomatics Research Australasia，2000，72:1-24.

［4］ VALANIS A，TSAKIRI M.Automatic target identification for laser scanners［C］//Proceedings of XXth ISPRS Congress.Istanbul，Turkey:International Society for Photogrammetry and Remote Sensing，2004:1-7.

［5］ ZHOU Sh G，TIAN H，LI H.A new automatic method for registering of point clouds［J］.Geotechnical Investigation ＆ Surveying，2012，40(2):66-69(in Chinese).

［6］ WANG L，LI G Y，ZHANG H X.Automatic recognition method of planar target based on return light intensity ［J］.Infrared and Laser Engineering，2011，40(10):1910-1913(in Chinese).

［7］ CHEN J J，YAN W T.Research on algorithm for extraction of target center coordinates based on the point clouds［J］.Journal of Geotechnical Investigation ＆ Surveying，2013，41(8):53-57(in Chinese).

［8］ CANG G H，YUE J P.Plane fitting of point clouds based on weighted total least square［J］.Laser Technology，2014，38(3):307-310(in Chinese).

［9］ GUAN Y L，LIU Sh T，ZHOU Sh J，et al.Robust plane fitting of point clouds based on tls［J］.Journal of Geodesy and Geodynamics，2011，31(5):80-83(in Chinese).

［10］ GAO X W，SUN L，XIE H Q.Research on accuracy impact of target color and roughness to 3-D laser scanning point cloud［J］.Bulletin of Surveying and Mapping，2013(11):84-86(in Chinese).

［11］ WALTER G R.Thesingularvaluedecomposition ［EB/OL］.［2008-12-12］.http://www.math.ethz.ch/education/bachelor/lectures/hs2012/other/linalg_INFK/svdneu.pdf.

［12］ PETRá? I，BEDNáROVá D.Total least squares approach to modeling:a Matlab toolbox［J］.Acta Montanistica Slovaca，2010，15(2):158-170.