索支撐壓桿屈曲性能分析

梁笑天，袁行飛

（浙江大學 空間結構研究中心，浙江 杭州310058）

在大跨度空間結構體系迅速發展的近20年中，以索、桿結構為基礎的組合形式一直被國內外工程師所廣泛使用，如1996年亞特蘭大奧運會主體育場——喬治亞穹頂采用了索穹頂結構；2008年北京奧運會主場館——北京工業大學體育館采用了弦支穹頂結構.索穹頂結構是由脊索、斜索和環索構成的連續張力索網和不連續的壓桿組成；弦支穹頂結構則是由上層單層球面網殼和下層環索、斜索通過豎桿連接而成［1］.在這些結構中，壓桿兩端或一端與索連接，故稱其為索支撐壓桿.在現有的整體結構有限元分析中，通常將壓桿直接簡化為單個桿單元，因此，只能考慮結構整體失穩或由于節點的塌陷導致的局部失穩，而不能考慮壓桿屈曲對于結構性能的影響［2-4］.目前，采取吳柏生［5-6］所提出的計算方法進行彈性支撐壓桿的失穩計算，其指出存在一個由桿的長度以及抗彎剛度決定的支撐剛度閾值（Kcr），即當支撐剛度從0增加到該閾值時桿的屈曲荷載也隨之增加，而當支撐剛度超過該閾值時桿的屈曲荷載與兩端剛性支撐鉸支桿相同.對于張拉整體結構，國內羅堯治等［7］取閾值Kcr=；對于索穹頂結構，闞遠等［8］取閾值Kcr=.本文采用彈性支撐鉸支桿模型，對大跨空間結構中常用的兩類索支撐壓桿——兩端索支撐壓桿和一端剛性桿支撐一端索支撐壓桿利用ANSYS軟件進行非線性有限元分析，探討支撐索不同初始預應力、壓桿初始缺陷和支撐桿不同剛度對壓桿及索桿單元穩定性的影響.

1 彈性支撐壓桿屈曲分析相關理論與計算假定

1.1 彈性支撐壓桿屈曲分析理論

設一長為L，抗彎剛度為EI（E為彈性模量，I為截面慣性矩）的桿兩端鉸接于剛度為K的彈性支撐上，一端承受大小為P的橫向荷載（圖1）.

圖1 兩端彈性支撐鉸支桿Fig.1 Centrally compressed strut with elastic restrains

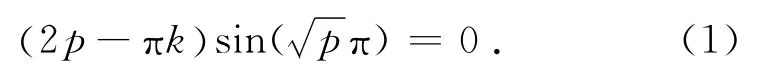
將原有變量代入式（1）可得

當K＜Kcr時，最小屈曲荷載Pcr=KL／2；當K≥Kcr時，最小屈曲荷載Pcr=π2EI／L2，即此時的屈曲荷載等于兩端鉸支桿的屈曲荷載.

式（3）與文獻［7］中的閾值取值相同，與文獻［8］中的閾值取值不同的原因是選取的計算模型不同.前者選取的是兩端鉸支桿的計算模型，而后者選取的是兩端夾緊桿的計算模型.考慮到索和桿的實際連接方式，認為兩端鉸支桿的計算模型更為準確.

1.2 預應力索的剛度

由于索本身具有“只拉不壓”的特殊性質，索的

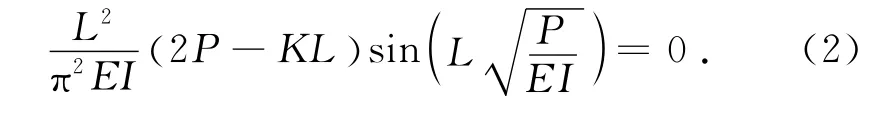
有實際意義的僅是最低的屈曲荷載，于是可得到支撐剛度閾值受力狀態與普通彈性支撐存在一定的區別.索的剛度由3部分組成：彈性剛度、重力剛度和幾何剛度.彈性剛度取決于索的彈性模量、截面積和受力狀態.當索處于受拉狀態時，彈性剛度服從胡克定律；當索力減小至0時，喪失軸向彈性剛度.重力剛度則只有在索擁有充分垂度時才會逐漸顯現出來，不同于懸索結構，索桿張力結構中索的長度一般較短，重力剛度一般可以忽略不計.幾何剛度存在于與索軸相垂直的方向，與索拉力和長度有關，但是一般比彈性剛度和重力剛度小得多［9］.

假設索在初始態的長度為L0，預應力態的長度為L1，荷載態的長度為L，則支撐壓桿的索的總彈性剛度為

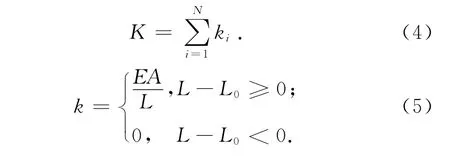
式中：N為支撐壓桿的索根數，E為索彈性模量，A為單根索截面積，k為單根索的彈性剛度.對內蒙古伊旗全民健身體育中心索穹頂結構體系［10］進行分析，支撐壓桿的彈性模量取2.06×105MPa，根據式（3）計算得到不同尺寸的壓桿的支撐剛度閾值如表1所示，選用Q345 B鋼材可以保證表中所列壓桿在彈性范圍內屈曲.而對于預應力索，彈性模量取1.9×105MPa，索型號為 Φ32，長10 m，則根據式（5）計算得到預應力索對壓桿提供的支撐剛度為15 281 k N／m，遠大于表1中壓桿的支撐剛度閾值.以上計算表明：此時僅單根索提供的支承剛度足以使得壓桿的屈曲荷載與兩端鉸支約束的桿件屈曲荷載相同.對不同尺寸及形式的結構的大量計算結果表明：對于絕大多數索桿張力結構，在預應力索不松弛的情況下，兩端有索支撐的壓桿的臨界荷載可取計算長度為原長的壓桿臨界荷載值.

1.3 計算假定

對兩類索支撐壓桿——兩端索支撐壓桿和一端剛性桿支撐、一端索支撐壓桿受力性能進行數值模擬，分析中采用如下假定：

1）兩端索支撐壓桿模型中，索與壓桿連接的一端為鉸接，另一端為固接；

2）一端剛性桿支撐一端索支撐的壓桿模型中，剛性桿和索與壓桿連接的一端為鉸接，另一端為固接；

3）2種計算模型中壓桿的兩端均可移動，移動幅度取決于上下索的剛度、預應力和剛性桿的剛度.

表1 已建工程中壓桿支撐剛度閾值計算Tab.1 Calculation of rods'support stiffness threshold in established project

2 兩端索支撐壓桿受力性能

在索穹頂結構中，壓桿兩端與上部脊索、下部斜索及環索相連.建立兩端分別與3根索相連的壓桿模型（圖2），壓桿使用BEAM 188單元，為模擬壓桿的屈曲，壓桿在建模中用多段梁單元代替桿單元.壓桿長度為10.00 m，外徑為0.20 m，內徑為0.18 m，彈性模量為2.06×105MPa.拉索長度為6.00 m，直徑為0.04 m，彈性模量為1.90×105MPa，每根索與壓桿的夾角為60°，使用LINK 10單元模擬.索的一端固接，另一端與壓桿端部耦合，索初始應變為0.001 0.

采用有限元進行壓桿的非線性屈曲分析，當壓桿的單元劃分數在8個以上時，其臨界荷載穩定在某一固定值［11］.本例中壓桿劃分為10個梁單元.對桿件施加初始缺陷，缺陷采用正弦半波的形式y=，式中L0為桿件長度，N=250.

2.1 壓桿屈曲全過程分析

兩端預應力索約束下的壓桿模型如圖2所示，對壓桿上節點施加沿壓桿軸向的荷載，壓桿發生變形，如圖3所示.壓桿受力過程中節點的荷載-位移曲線如圖4所示，其中位移為已扣除壓桿支座位移的頂端軸向位移.

在荷載施加初始階段，節點荷載-位移曲線基本為線性，對應上部索力逐漸減小.當荷載增加到423.56 k N（點a）時，上部支撐索索力Fc為零（圖5），索松弛，但此時單元仍能繼續承載，壓桿的內力繼續增大（圖6）.

當壓桿的內力FN增加到512.56 k N（點b）時，節點荷載-位移曲線與壓桿內力-位移曲線斜率均發生較大變化.荷載增加較緩慢時，壓桿頂點位移即迅速增大，此時可認為桿件發生屈曲.

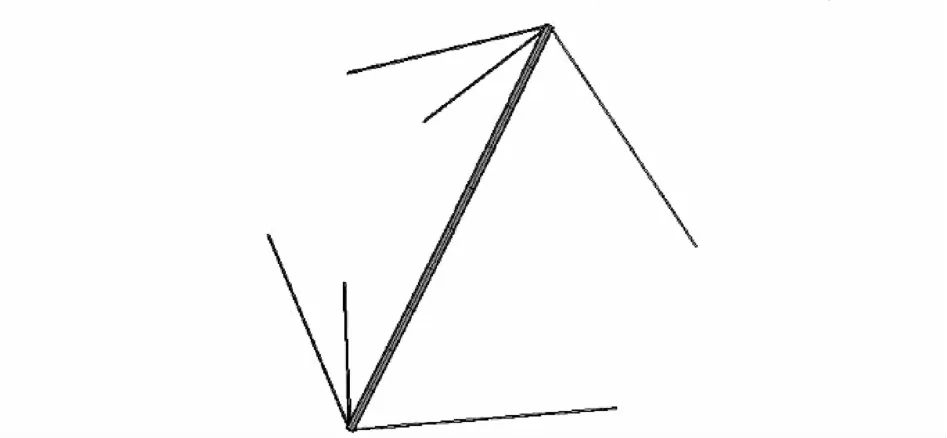
圖2 兩端預應力索約束下的壓桿Fig.2 Strut supported by prestressed cables

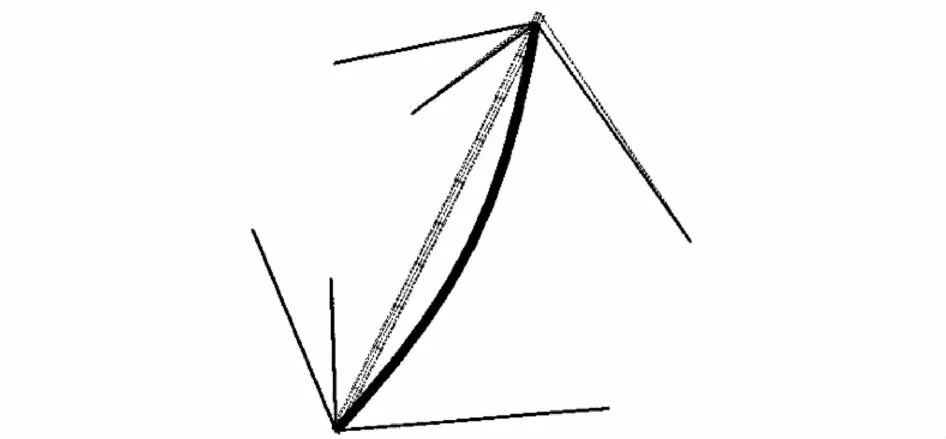
圖3 索桿結構變形圖Fig.3 Deformation of cable-strut element

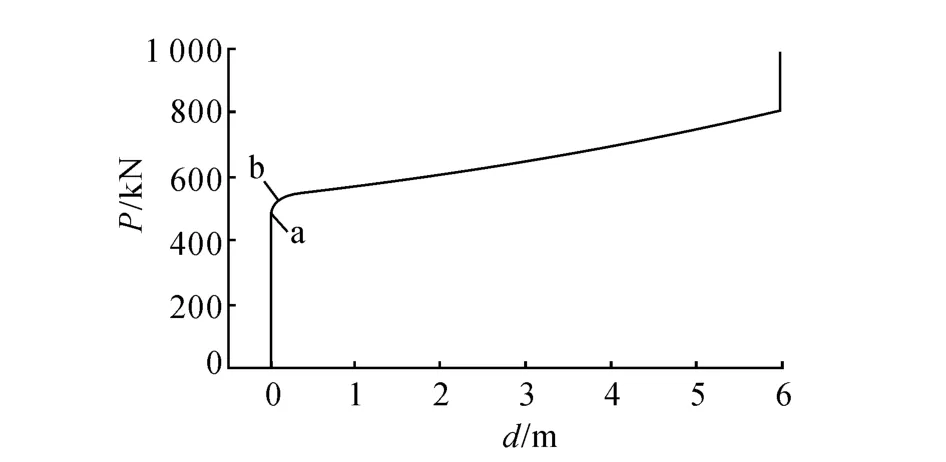
圖4 節點荷載-位移曲線Fig.4 Nodal load-displacement curve

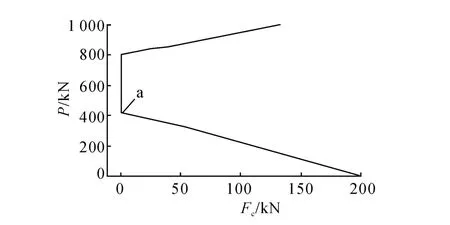
圖5 上部索內力隨外荷載變化曲線Fig.5 Relationship between nodal load and upper cableforce

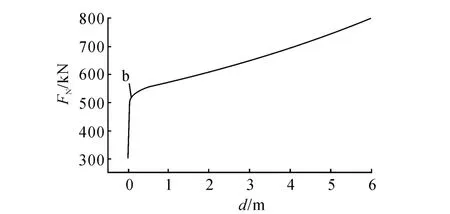
圖6 壓桿內力-位移曲線Fig.6 Relationship between internal force of strut and displacement

上例中的壓桿若按照兩端鉸支約束計算，則其臨界荷載為

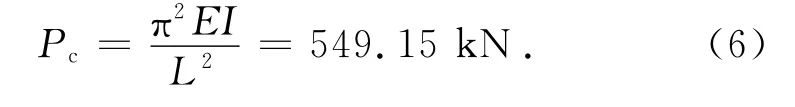
非線性分析得到的屈曲荷載512.56 k N與式（6）相近，由于初始缺陷的影響，比上述歐拉臨界荷載略小.

2.2 索初始預應變的影響

對索施加不同初始預應力可通過改變索初始預應變實現，在外荷載不斷增加的過程中，索內力基本線性減小（圖7）.ε為索初始應變，而節點荷載-位移曲線斜率亦保持不變.當上部拉索內力Fc減小至0后，節點荷載-位移曲線斜率發生變化（圖8），此后，索初始預應變的不同對于結構的受力情況影響不大，不同初始預應力下結構的節點荷載-位移曲線逐漸趨近.

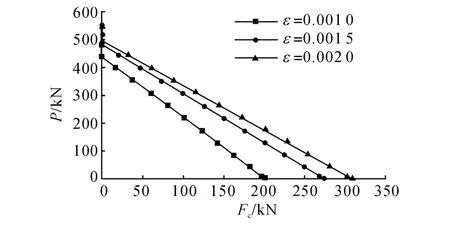
圖7 不同預應變下索力隨荷載變化圖Fig.7 Internal force of cable with different initial strain

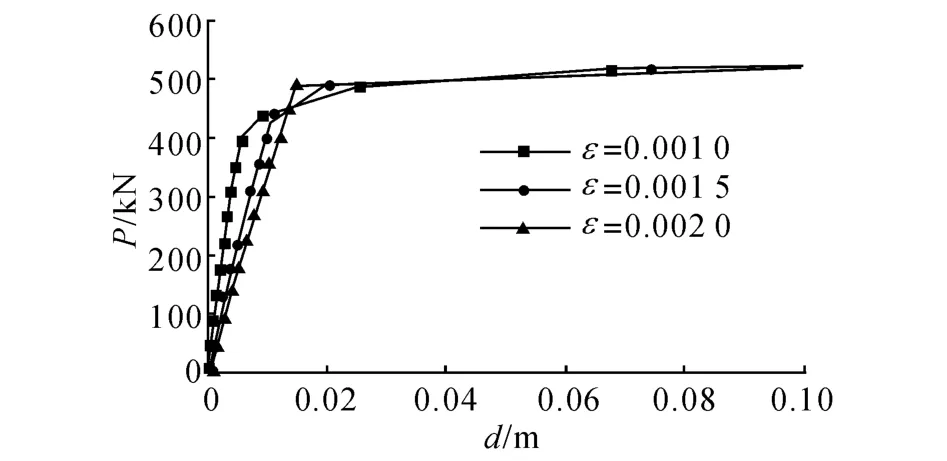
圖8 不同預應變下結構的節點荷載-位移圖Fig.8 Nodal load-displacement curve of cable-strut element with different initial strain

2.3 初始缺陷的影響

對壓桿引入不同幅值的初始缺陷，得到圖9所示的節點荷載-位移曲線，δ為壓桿初始缺陷.在施加荷載前期，不同缺陷的桿件差別不大，因為此時結構由上部預應力索承擔了較大外荷載，達到臨界荷載后，缺陷的大小對于壓桿的受力性能存在影響，但是影響不大.

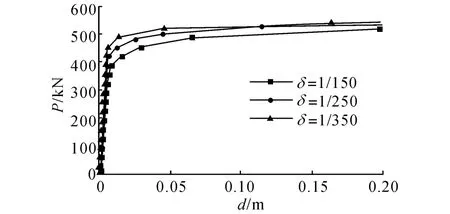
圖9 不同缺陷下結構的節點荷載-位移圖Fig.9 Nodal load-displacement curve of cable-strut with different initial imperfections

3 一端剛性桿支撐、一端索支撐的壓桿受力性能

弦支穹頂中壓桿一端與單層球面網殼的節點相連，一端與預應力拉索連接（如圖10所示），共同發揮單層網殼和張拉體系的優勢.弦支穹頂剛度比索穹頂大，中間壓桿的受力性能很大程度上取決于上部桿件的剛度及桿件與壓桿之間的角度.取壓桿長度為5.00 m，外徑為0.15 m，內徑為0.13 m，上部桿件直徑為0.10 m，長度為2.61 m，夾角為85°.桿件連接壓桿的一端鉸接，另一端固接.拉索長度3.00 m，直徑為0.04 m，彈性模量為1.90×105MPa，每根預應力索與壓桿夾角為60°，索初始應變為0.002 0.在非線性有限元計算中，采用BEAM188單元模擬上部剛性桿，使用弧長法求解.

3.1 索桿單元屈曲全過程分析

在上部桿件與壓桿的交點處施加荷載，方向沿壓桿軸向，節點荷載-位移曲線為非線性，如圖11所示.當壓桿內力FN=661.12 k N（圖12中點a）時，壓桿首先發生屈曲，由于上部壓桿的約束，壓桿不會發生過大位移.整個體系仍保有承載能力，可繼續承載，直到達到最大荷載1 396.99（點b），此時壓桿內力為692.15 k N，上部桿件的軸力Fu為4 362.18 k N（圖13）.繼續跟蹤節點荷載-位移曲線，整個體系

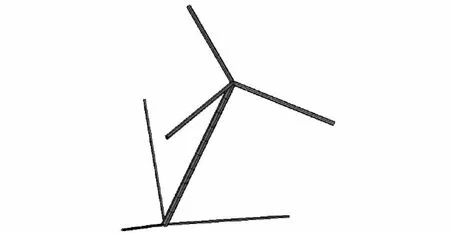
圖10 弦支穹頂中的壓桿單元Fig.10 Cable-strut element in suspen-dome

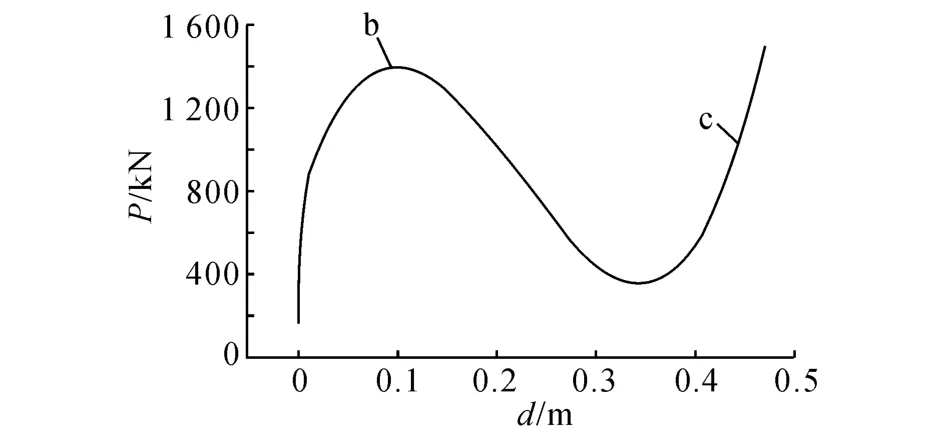
圖11 節點荷載-位移曲線Fig.11 Nodal load-displacement curve

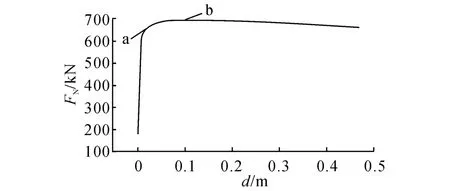
圖12 壓桿內力-位移曲線Fig.12 Relationship between internal force of strut and displacement

圖13 上部桿件軸力隨節點荷載變化曲線Fig.13 Relationship between nodal load and upper rigid rods force

由于初始缺陷的影響，上式結果稍大于點a對應的荷載值661.12 k N.由此可見，一端剛性桿支撐一端索支撐的壓桿雖然先發生屈曲，但是由于上部桿件的約束作用，體系仍然可以繼續承載，直至整個壓桿體系失穩.

3.2 索初始預應力的影響

不同索預應力情況下，在承受荷載初期，3種不同模型的結構節點荷載-位移曲線（見圖14）和壓桿內力-位移曲線（見圖15）基本重合.索桿單元中的出現類似空間網殼結構典型的跳躍失穩現象，上部桿件軸力在短時間內由4 362.18k N（點b）降為0（點c），此時節點荷載值降為1 049.25 k N.

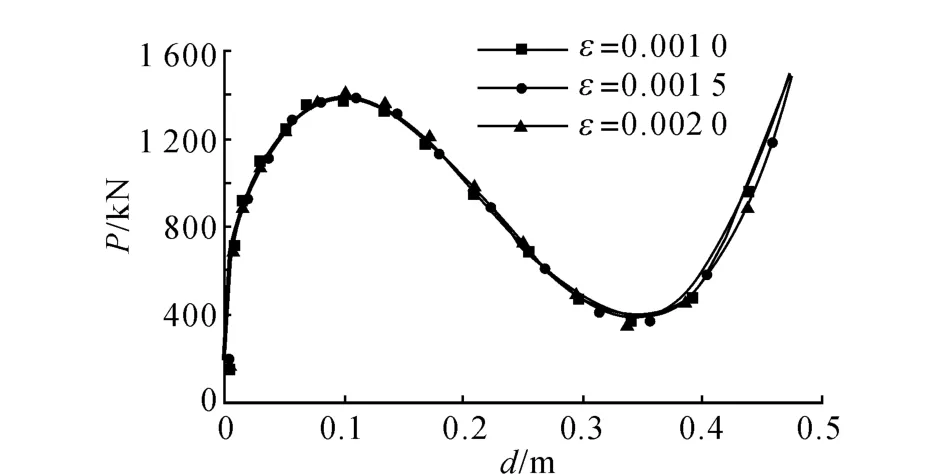
圖14 不同預應變下結構的節點荷載-位移曲線Fig.14 Nodal load-displacement curve of cable-strut with different initial strain

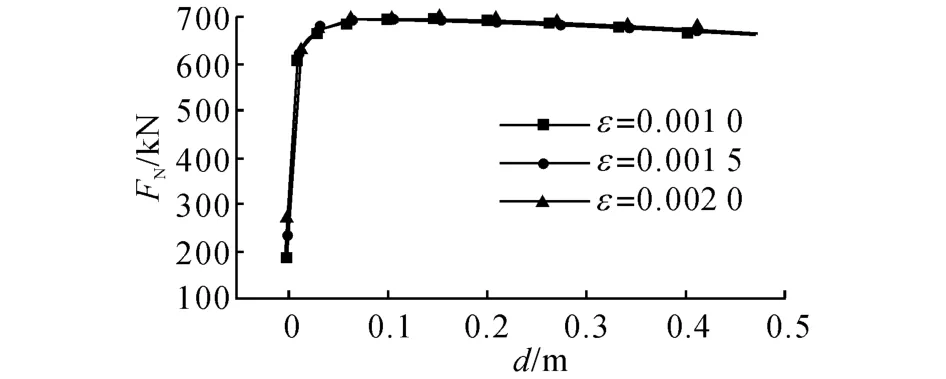
圖15 不同預應變下結構的壓桿內力-位移曲線Fig.15 Relationship between internal force of strut and displacement with different initial strain

索桿單元屈曲全過程分析中的壓桿若按照兩端鉸支約束計算，則其臨界荷載為壓桿先于整個體系屈曲，預應力只對壓桿初始內力有影響，而對結構的整體剛度影響不大，原因是此時預應力索只存在于索桿單元下部，隨著結構的變形，下部索拉力持續增大，不會出現如兩端均為索支撐的壓桿單元中上部拉索松弛的現象，故對于由預應力索和上部桿件共同作用的索桿單元，索預應力對結構的影響不明顯.節點荷載-位移曲線何時進入下降段主要取決于上部桿件達到極值點的時間.

3.3 上部桿件剛度的影響

改變上部桿件的截面積，研究上部桿件剛度對壓桿性能的影響，得到節點荷載-位移曲線（圖16）和壓桿內力-位移曲線（圖17），D為上部桿件的直徑.可以看出，索桿單元中的壓桿先于整個體系屈曲，壓桿內力-位移曲線不會因上部桿件剛度的不同而發生變化.但是在節點荷載-位移曲線中，當荷載較小時，上部桿件直徑不同對曲線的影響不大，隨著荷載的繼續增大，壓桿屈曲后，曲線呈非線性變化，3條曲線的極值點值分別為1 135.31、1 256.70和1 396.99 k N.壓桿屈曲荷載不會因上部支撐桿件剛度的不同而發生改變，接近于式（7）的計算結果.整個壓桿體系屈曲荷載將隨著上部剛性桿面積的增大有不同程度的提高.

4 結 論

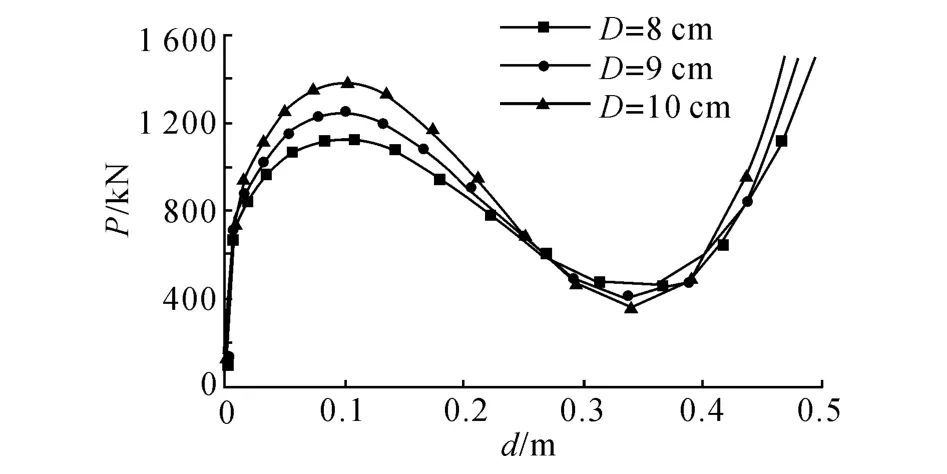
圖16 不同剛度上部桿件對應的節點荷載-位移曲線Fig.16 Nodal load-displacement curve of cable-strut with different rigidity of upper rods

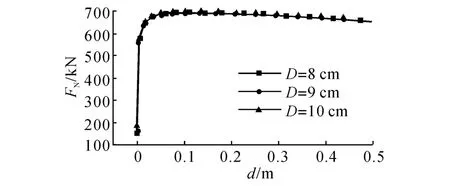
圖17 壓桿內力-位移曲線Fig.17 Relationship between internal force of strut and displacement

（1）兩端索支撐壓桿的屈曲荷載基本符合吳柏生［5-6］所提出的計算方法，壓桿內力-位移曲線斜率發生較大轉折處對應的荷載值接近于按照兩端鉸支計算的桿的歐拉臨界荷載.

（2）兩端索支撐壓桿中，索的預應力對于節點荷載-位移曲線存在影響，當上部預應力索松弛后節點荷載-位移曲線斜率會發生變化，此時壓桿只有下部索的支撐.

（3）對于一端索支撐一端剛性桿支撐的壓桿，壓桿的屈曲先于整個壓桿體系的屈曲，壓桿的臨界荷載值可以近似取為按照兩端鉸支桿的歐拉臨界荷載.在壓桿屈曲后，由于上部桿件的約束作用，結構仍然可以繼續承載，直至上部桿件發生跳躍屈曲使得結構整體失穩.

（4）本文研究了不同彈性支撐對單個索桿單元屈曲性能的影響，考慮到實際工程中通常存在多個單元的連接，且各單元之間存在相互作用，因此，單個索桿單元中的壓桿發生屈曲后的結構整體穩定性仍然有待研究.

（

）:

［1］董石麟，羅堯治，趙陽，等.新型空間結構分析、設計與施工［M］.北京：人民交通出版社，2006：385.

［2］袁行飛，周練，李阿龍.基于求解運動路徑的非線性力學的結構屈曲路徑跟蹤研究［J］.土木工程學報，2013，46（6）：82- 89.YUAN Xing-fei， ZHOU-Lian， LI A-long.Buckling analysis of structures based on geometrically nonlinear force method by solving kinematic path（GNFM-KP）［J］.China Civil Engineering Journal，2013，46（6）：82- 89.

［3］錢若軍，袁行飛，林智斌.固體和結構分析理論及有限元法［M］.南京：東南大學出版社，2013：590- 599.

［4］許國杰，卓新，壽全根，等.TH-Levy型索穹頂局部構件失效時的受力性能［J］.浙江大學學報：工學版，2011，45（7）：1281- 1287.XU Guo-jie，ZHUO Xin，SHOU Quan-gen.Structural performance of TH-Levy cable dome when local component failure［J］.Journal of Zhejiang University：Engineering Science，2011，45（7）：1281- 1287.

［5］吳柏生.兩端彈性支承夾緊桿的后屈曲分析［J］土木工程學報，1997，30（2）：42- 48.WU Bai-sheng.Post buckling analyses of elastically supported strut with two clamped ends［J］.China Civil Engineering Journal，1997，30（2）：42- 48.

［6］吳柏生.兩端彈性支承鉸支桿的后屈曲分析［J］.工程力學（增刊），1996，（A02）：612- 616.WU Bai-sheng.Post buckling analyses of elastically supported strut with two hinged ends［J］.Engineering Mechanics（supple.），1996，（A02）：612- 616.

［7］羅堯治，年有增，符剛.基于壓桿失穩的張拉整體結構極限承載力［J］.空間結構，2004，10（1）：7- 10.LUO Yao-zhi，NIAN You-zeng，FU Gang.Ultimate loadcarrying capacity of tensegrity based on the buckling of struts［J］.Spatial Structures，2004，10（1）：7- 10.

［8］闞遠，葉繼紅.索穹頂結構在靜力荷載作用下的失效分析［J］.特種結構，2007，24（3）：85- 88.KAN Yuan，YE Ji-hong.Failure analysis of cable dome structure under static loads ［J］.Special Structures，2007，24（3）：85- 88.

［9］肖恩源.索的特性［J］.公路，1997，5：1- 7.XIAO En-yuan.Characteristics of cable［J］.Highway，1997，5：1- 7.

［10］張國軍，葛家琪，王樹，等.內蒙古伊旗全民健身體育中心索穹頂結構體系設計研究［J］.建筑結構學報，2012，33（4）：12- 22.ZHANG Guo-jun，GE Jia-qi，WANG Shu，et al.Design and research on cable dome structural system of the National Fitness Center in Ejin Horo Banner，Inner Mongolia［J］.Journal of Building Structures，2012，33（4）：12- 22.

［11］田偉.剛性單層網殼結構找形與穩定研究［D］.杭州：浙江大學，2011：97- 100.TIAN Wei.Form-finding and stability research of rigid single-layer lattice shells ［D］.Hangzhou：Zhejiang University，2011：97- 100.