改進的Logistic映射及其動力學特性*

韓春艷， 禹思敏

(1.廣東工業大學自動化學院，廣東 廣州 510006；2. 濱州學院物理與電子科學系，山東 濱州 256603)

?

改進的Logistic映射及其動力學特性*

韓春艷1，2， 禹思敏1

(1.廣東工業大學自動化學院，廣東 廣州 510006；2. 濱州學院物理與電子科學系，山東 濱州 256603)

為了獲得性能良好的混沌偽隨機序列，分別采用尺度變換、構建魯棒性系統和復合映射的方法對Logistic映射進行改進。 Logistic映射的尺度變換可任意擴展滿映射區間和混沌區間，能夠改善序列的隨機特性，增大密鑰空間；構建魯棒性系統可使其在一定條件下呈現具有恒定Lyapunov指數的恒定混沌狀態，形成魯棒混沌映射；復合映射能夠成倍提高Lyapunov指數，可改善映射的初值敏感性和隨機性。因此，改進的Logistic映射可作為偽隨機序列發生器的隨機信號源，在保密通信、密碼系統和計算機等領域將有良好的應用潛力。

混沌； Logistic映射； 魯棒混沌映射； 復合映射

混沌具有初值敏感性和不可預測性[1]，它可產生性能良好的偽隨機序列而應用于密碼系統和保密通信等領域之中。

離散混沌由于其算法簡單及處理時運算速率快而在混沌應用中得到了廣泛的研究[2-6]，其中Logistic映射又是研究最早和應用最多的一種離散映射，使其成為一種典型的偽隨機序列信號源。文獻[7]提出了一個基于變形Logistic映射的流密碼方案，之后得到了廣泛關注和引用，很多混沌偽隨機序列發生器的設計都采用了Logistic映射[2-8]。直到最近幾年仍有大量文獻研究Logistic的基本特性及其變形，以及在保密通信和信息加密中的應用[9-14]。

但Logistic映射只有一個初值和一個參數，且參數范圍和滿映射區間都較小，混沌映射區間更小，致使其密鑰空間不大序列安全性較低；其混沌映射范圍與系統參數存在定量的函數關系，將降低密鑰參數的安全性。另外，Logistic映射的Lyapunov指數也不大，這意味著其初值敏感性不好[10]，因為Lyapunov指數越大，從2個不同初值出發的相鄰軌道在相同時間的演化過程中的分離距離就越大，其初值敏感性就越好，由初值的不確定性所導致的混沌長期演化的不可預測性，即隨機性就越好。更為重要的缺陷是，Logistic映射并不是魯棒混沌映射，分岔過程中存在很多周期窗口，當參數發生微小攝動時系統容易進入周期狀態。

本文基于如何擴展混沌映射區間和系統參數區間，如何提高系統的Lyapunov指數以及改善混沌映射的魯棒性等問題，利用尺度變換、魯棒性改進和復合映射方法對Logistic映射進行了改進，對其動力學特性進行了分析，發現該映射可任意擴展其參數區間、混沌區間和滿映射范圍，滿足一定條件，該映射呈現一種強魯棒性的恒定Lyapunov指數和恒定混沌狀態，復合映射則可使其Lyapunov指數成倍增加。

1 Logistic映射及其缺陷

Logistic映射有3種形式[10]，其動力學特性相類似。本文研究映射區間較大的形如式(1)的Logistic映射：

(1)

μ∈[0,μm]=[0,2];xn∈[-μm,μm]μm為參數μ的最大值。該映射數學結構簡單，其分岔圖如圖1所示。從把混沌作為一種隨機信號源的角度考慮，該映射存在如下需要改進之處：

(1)該映射只有一個參數，且映射參數區間較小，僅為μ∈ [0，2]；其混沌參數區間更小，約為[1.4，2]。用其產生偽隨機序列時，必使其工作于參數范圍約為0.6的混沌區間，因此較少的映射參數和較小的混沌參數范圍將導致較小的密鑰空間。

(2)滿映射時有較強的混沌狀態，但該映射僅在μ= 2時才是滿映射，且滿映射區間僅為I=[-2，2]。 較小的映射區間導致在迭代過程中其迭代值的變化范圍較小，亦即平均每次迭代的數值變化率小，根據迭代值變化而進行量化所獲得的二值[0，1]序列，其“0”、“1”的交替變換的速率將會降低，影響此二值序列的隨機特性。

(3)用于加密的混沌映射要求為魯棒混沌或是結構穩定的混沌映射，是指參數在具有小擾動的情況下所獲得的混沌映射和原混沌映射具有拓撲等價性。 然而Logistic映射并不是魯棒混沌映射，因為映射混沌區域中包含著稠密的周期窗口，當參數發生微小攝動時系統容易進入周期狀態。

(4)Lyapunov指數較小，μ=2時的最大指數僅為0.693 21。 較小的Lyapunov指數會降低混沌映射的初值敏感性，從而影響混沌序列的隨機性能，因為混沌的隨機性來源于其對初始條件的高度敏感性。

為克服上述不足，需要對Logistic映射進行改進，以提高其動力學性能。

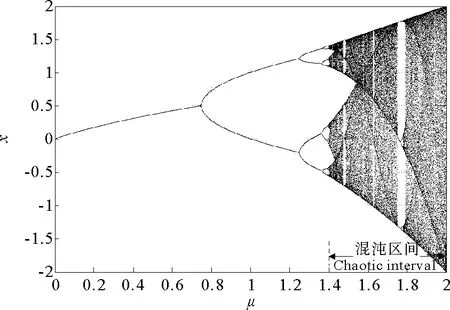
圖1 Logistic映射分岔圖Fig.1 The bifurcation diagrams of the Logistic map

2 Logistic映射的空間尺度變換

2.1 空間尺度變換

為了擴展映射區間，在式(1)的非線性項部分乘以一個放大因子1/β，有

(2)

β> 0，β∈ R。下面的分析將證明，μ∈[0，2β]，x∈ [-2β， 2β]。

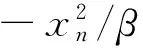
(3)

根據式(1)，由于區間端點處滿足xe=μ，因此把式(3)的μ換為xe后可得式(2)的映射區間為

xe=2β

(4)

即映射區間

I=[-xe,xe]=[-2β, 2β]=[-μm,μm]

(5)

由式(4)和(5)得，參數μ的范圍為[0，2β]，圖2(a)中的β= 2。式(2)的分岔圖如圖2(b)所示。

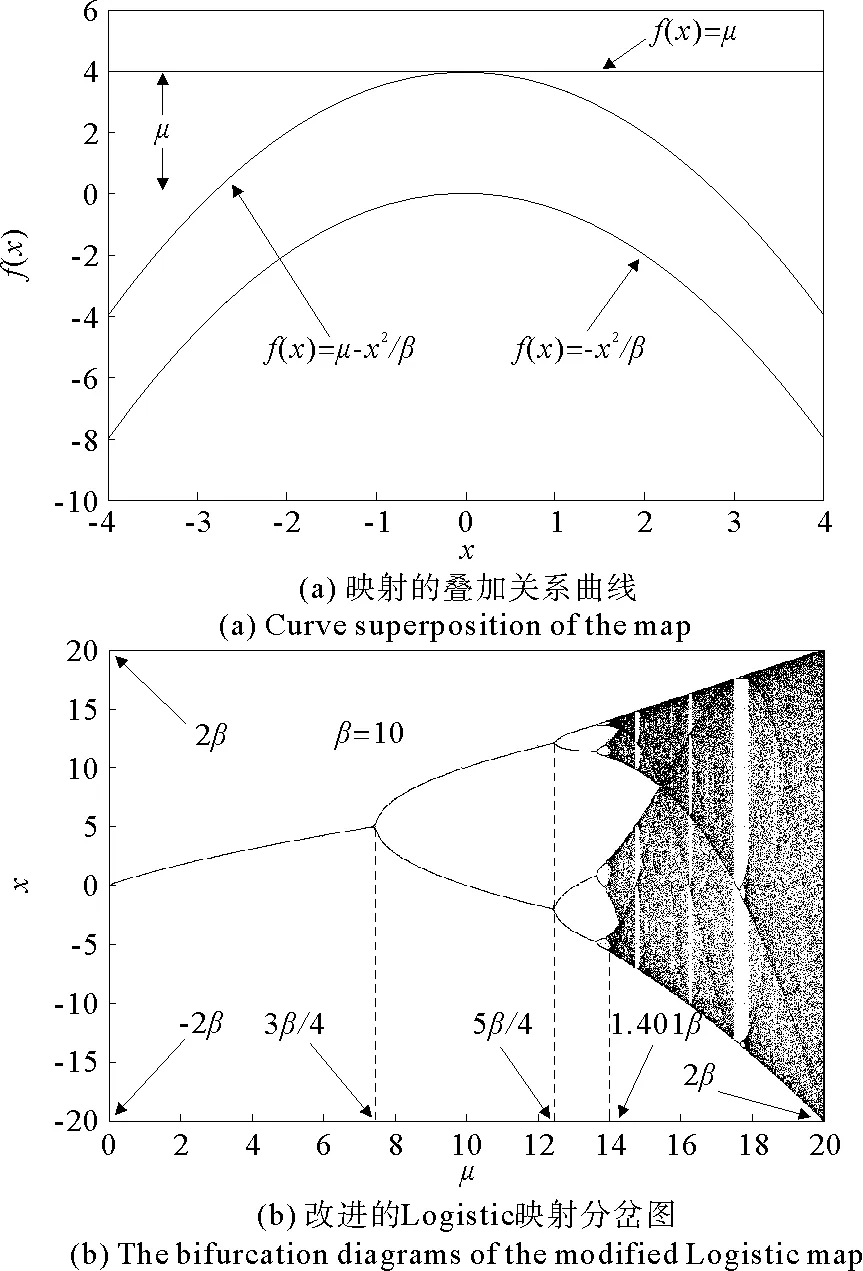
圖2 改進的Logistic映射Fig.2 Modified Logistic map

原映射參數μ被限制在[0，2]內，滿映射區間被限制在[-2，2]內。改進后的映射參數范圍和滿映射區間都被擴大為原來β倍，即μ∈[0, 2β]，xn∈[-2β,2β]，因此也可把β稱之為倍增因子。

2.2 動力學特性分析

現在考察參數變化時映射的運動形態。解不動點方程x=μ-x2/β得其不動點：

(6)

不動點的穩定性滿足

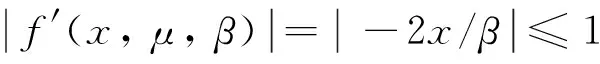
(7)

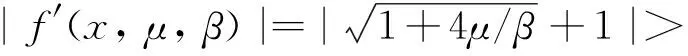
(8)

故得

(9)

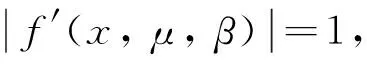
x=μ-(μ-x2/β)2/β

(10)

在方程(10)中還要排除x=f(x,μ,β)產生的周期1的解，因此只要解下面的方程即可：

(11)

解得：

(12)

f(f(x,μ,β))的導數為

[f(f(x,μ,β))]′=4x1x2/β2

(13)

周期2軌道穩定條件為

(14)

即

3β/4<μ<5β/4

(15)

在μ=5β/4時又發生倍周期分岔，如此演化最終在1.401β后周期趨于無窮大，進入混沌狀態，其混沌映射區間IC近似為：

IC=2β-1.401β=0.599β

(16)

因此，這種改進的Logistic映射除任意擴展滿映射區間IO=[-2β，2β]外，還可任意擴展其混沌映射區間IC=[1.401β，2β]，這是此種映射的主要優點。其實，與原映射相比，改進后的各種分岔參數都變為原分岔參數的β倍，因此亦可把β稱之為放大系數。

2.3 參數β的分岔特性

在參數μ的分岔特性中，不同的β對分岔參數影響很大，如從周期1到周期2的分岔參數μ=3β/4，從周期2到周期3的分岔參數μ=5β/4，準周期的分岔參數為1.401β。如果直接把β作為分岔參數，將會發生何種現象？

因為在改進的Logistic映射中，β和μ必須滿足一種μ=2β的關系才是合理的映射，如果不滿足這種關系，將會導致迭代值不在允許的映射區間內使其迭代無法進行，或將出現一些特殊的現象。

根據式(2)，μ∈[0, 2β]，即只有μ≤2β迭代才能在區間[-2β, 2β]進行。否則，如果μ>2β或2β<μ則無法進行迭代。圖3(a)是固定μ=15畫出的隨β變化的分岔圖，當2β<μ=15時無法迭代；但當2β≥μ=15時，沒經過任何演化過程突然進入混沌區，稱這種現象為“爆發混沌”。然后系統隨著β的增大進入一個倒倍周期分岔過程而進入周期1的穩定狀態。 這個演化過程和隨著μ增大而呈現的分岔過程正好相反，這是一個有趣的現象。

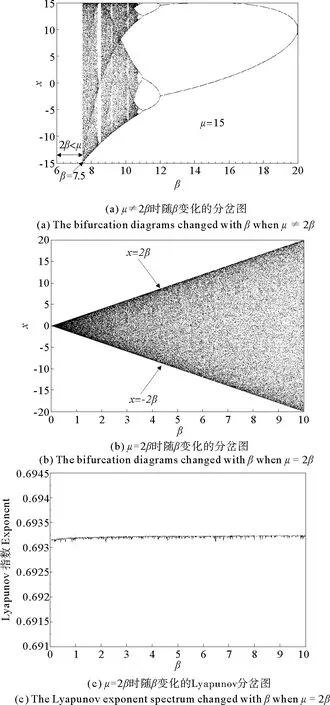
圖3 改進的Logistic映射的分岔圖與Lyapunov指數譜Fig.3 The bifurcation diagrams and the Lyapunov exponent spectrum of the modified Logistic map

3 Logistic映射的魯棒性改進

另一種最重要的分岔規律是，當式(2)μ滿足一定條件時，改進的Logistic映射呈現一種恒定混沌和恒定Lyapunov指數現象，表現出其強魯棒性。

據式(2)和圖2，當滿足μ=2β時改進的Logistic映射呈現一種滿映射的強混沌狀態，此時Lyapunov指數也最大。 如果令式(2)中μ=2β，即

(17)

且把β作為分岔參數，當β變化時μ同步變化并始終滿足μ=2β，式(17)將出現一種恒定混沌和恒定Lyapunov指數的現象，且對應著一種恒定的滿映射(滿映射區間xn∈[-2β, 2β])，其分岔圖和Lyapunov指數譜如圖3(b)、(c)所示。計算Lyapunov指數時取初值x0= 0.1，每計算一個指數值迭代求解方程50000次，恒定指數值為0.69321。

利用這種恒定混沌現象可設計一個恒定混沌信號發生器，此種情況下出現混沌的β參數區間將趨于無窮大，這意味著有趨于無窮大的密鑰空間，且映射區間也將隨同趨于無窮，這在實際應用中將有重要的意義。

適合作為加密的混沌映射應是魯棒混沌或至少是結構穩定的混沌映射[15]。但無論Logistic映射還是改進的Logistic映射在其混沌區間都有稠密的周期窗口，當系統參數存在擾動驅使系統運動到周期軌道時，擾動下的映射與原混沌映射不是拓撲等價的，因而式(1)和(2)就不是魯棒的混沌映射。

當式(2)滿足μ=2β條件而成為恒定混沌映射(17)時，無論參數β如何變化，系統始終維持恒定Lyapunov指數的恒定混沌狀態，這說明此時系統是魯棒的和結構穩定的，即不會因參數β的擾動或微小變化而使得改進系統由原來的混沌態進入到非拓撲等價的周期態。

綜上所述，通過空間尺度變換任意擴展了混沌映射的參數區間和滿映射的值域區間，恒定混沌映射把混沌映射區間由原來的[1.4，2]擴展為[0，∞]，在其動力學特性改善的同時，改進的Logistic映射仍保持了原來的結構簡單、運算速率快等特性。

4 Logistic映射的復合映射

用f(g(x))表示Rn到Rn的復合映射[16]。 映射f(x)自身的一個復合映射可表示為

xn+1=f(f(xn))=f2(xn)

(18)

由改進的Logistic映射得到的復合映射為

(19)

其中：μ∈[0, 2β]；xn∈[-2β, 2β]。雖然改進的Logistic映射(式(2))擴展了映射區間和混沌區間，但Lyapunov指數沒有提高。本文認為，提高Lyapunov指數是提高混沌系統隨機性的重要方法，尋找提升Lyapunov指數的方法是本文的另一重要目的。

為此，先看一下Lyapunov指數的定義[10]：

(20)

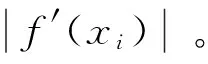
f′(f(x))f′(x)

(21)

根據式(20)，如果把式(18)的復合映射作為一種新的映射將提高其Lyapunov指數，即

(22)

由于f(xi)=xi+1，故

(23)

因此，把式(23)代入式(22)最后一個等號右端第一項，得

(24)

式(24)右端第二項為f(x)的Lyapunov指數Le，迭代初值取x0；而第一項為初值取x1(i= 0時，xi+1=x1)時同一個迭代函數f(x)的Lyapunov指數，在迭代次數n→∞時，式(24)右端兩項的極限相等，即

(25)

據式(24)和(25)得，離散復合映射f(f(x))的Lyapunov指數是單映射的二倍，即

LE=2Le

(26)

為便于比較，把改進的Logistic映射及其復合映射的Lyapunov指數譜畫在一個坐標系中，如圖4(a)所示。計算時取初值x0= 0.1，對每一指數的計算迭代50000次，當μ= 2β=20時，改進映射及其復合映射的最大Lyapunov指數分別為0.693 21和1.386 40，兩者近似為二倍關系，當迭代次數n→∞時兩者將趨于嚴格的二倍關系，從而證明了式(26)。

圖4(b)μ=2β時復合映射隨β變化的Lyapunov指數譜，與單映射相比，復合映射在相同條件下仍呈現一種恒定Lyapunov指數狀態，但其Lyapunov指數為1.386 40，是單映射的2倍。

雖然復合映射具有復雜特性和大的Lyapunov指數，但復合映射比單映射的數學運算復雜的多。如果復合映射的數學結構和運算過于復雜，用電子系統對其處理時速率就會降低，因此采用復合映射應針對結構和運算較為簡單的離散映射。但與連續混沌系統相比，離散映射比之由幾個一階非線性微分方程耦合而成的方程組的運算簡單的多，故一維離散映射的復合映射在實際中應有較好的應用潛力。

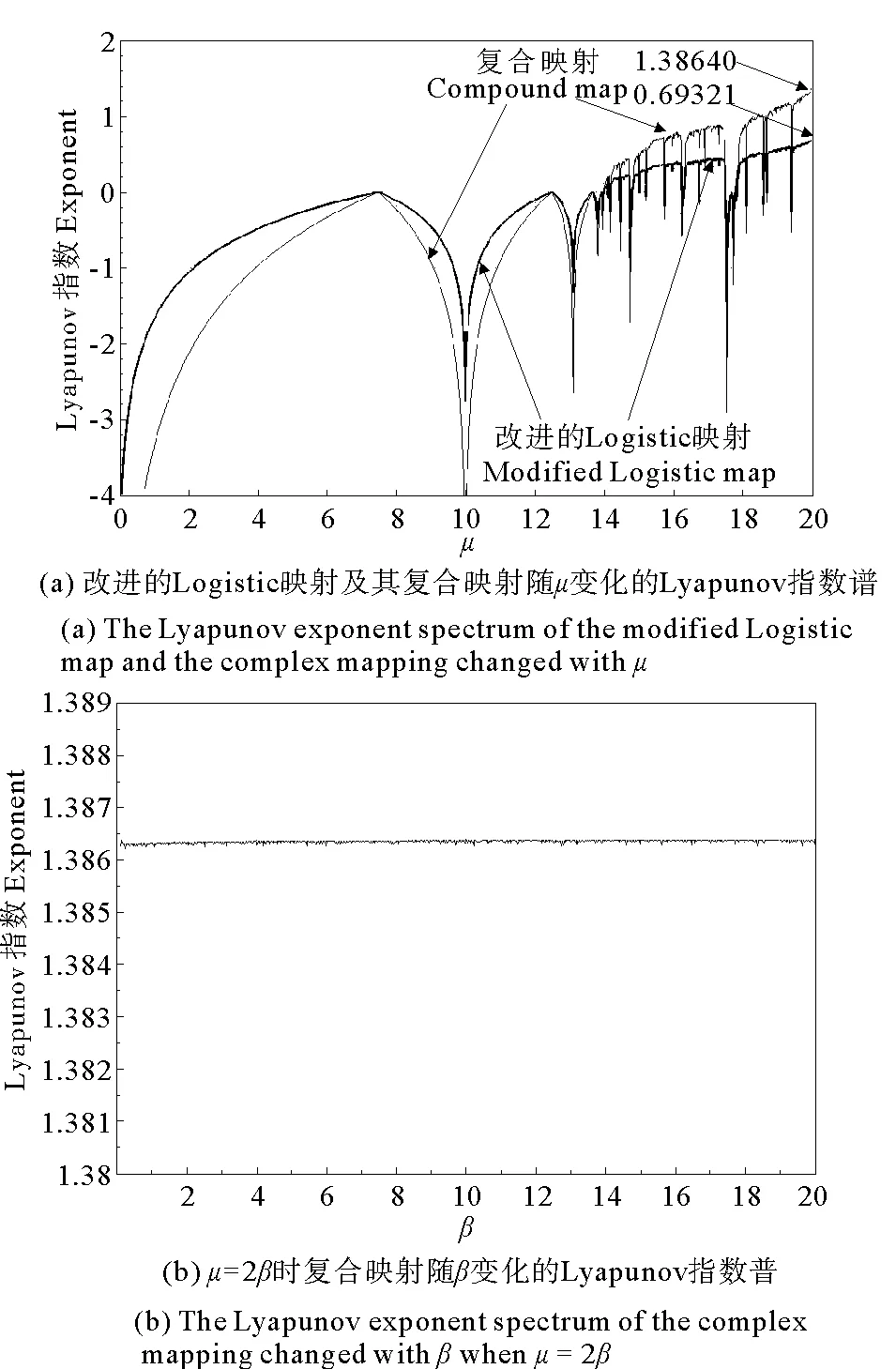
圖4 復合映射的Lyapunov指數譜Fig.4 The Lyapunov exponent spectrum of the complex mapping

5 結語

本文研究了一種改進的Logistic映射，對其動力學特性的改善進行了詳細分析通過引入一個新的參數即倍增因子β，使其映射區間和分岔參數范圍都擴大了任意的β倍；通過改進的Logistic映射構造了一個復合映射，該映射的最大優點在于把Lyapunov指數提升為原來的二倍；改進的Logistic映射及其復合映射在一定條件下都呈現一種恒定混沌或恒定Lyapunov指數的演化狀態以及魯棒性。改進的Logistic映射及其復合映射在應用方面有其自身的優勢：任意大的映射區間將提高混沌序列的變化率，任意大的混沌區間在理論上提供了趨于無窮的參數空間和密鑰空間，大的Lyapunov指數提高了混沌的初值敏感性，而魯棒性可使混沌映射更適合應用于保密通信之中。這些優勢將改善混沌偽隨機序列的隨機性和安全性，在混沌偽隨機序列發生器的設計及其應用中將有良好的應用潛力。

[1] Lorenz E N. The Essence of Chaos [M]. Washington: The University of Washington Press， 1993： 25.

[2] Persohn K J， Povinelli R J. Analyzing logistic map pseudorandom number generators for periodicity induced by finite precision floating-point representation [J]. Chaos Solitons & Fractals， 2012， 45(3)： 238-245.

[3] Narendra Singh， Aloka Sinha. Chaos-based secure communication system using logistic map [J]. Optics and Lasers in Engineering, 2010， 48(3)： 398-404.

[4] Chen S L， Chang S M， Lin W W， et al. Digital secure communication using robust hyper-chaotic systems [J]. Int J Bifurcation and Chaos， 2008， 18(11)： 3325-3339.

[5] Debabrata Dutta， Bhattacharjee J K. Period adding bifurcation in a logistic map with memory [J]. Physica, 2008， 237(23)： 3153-3158.

[6] Makisha P S Maier， Enrique P L. Switching induced oscillations in the logistic map [J]. Physics Letters A， 2010， 374(8)： 1028-1032.

[7] Robert Matthews. On the derivation of a “chaotic”encryption algorithm [J]. Cryptologia， 1989， 13(1)： 29-42.

[8] Chen S L， Hwang T T， Lin W W. Randomness Enhancement Using Digitalized Modified Logistic Map [J]. IEEE Trans Circuit Syst -II: EXPRESS BRIEFS， 2010， 57(12)： 996-1000.

[9] Thomas Curtright， Andrzej Veitia. Logistic map potentials [J]. Physics Letters A， 2011， 375(3)： 276-282.

[10] 王光義， 袁方. 級聯混沌及其動力學特性研究 [J]. 物理學報，2013，62(2)： 020506.

[11] 孟繼德， 包伯成， 徐強. 二維拋物線映射的動力學研究 [J]. 物理學報，2011，60(1)： 010504.

[12] 徐正光， 田清， 田立. 一類可以產生獨立同分布密鑰流的混沌系統 [J]. 物理學報， 2013， 62(12)： 120501.

[13] 姜海波， 李濤， 曾小亮，張麗萍. 周期脈沖作用下Logistic 映射的復雜動力學行為及其分岔分析 [J]. 物理學報， 2013， 62(12)： 120508.

[14] Mamta Rani a， Rashi Agarwal. A new experimental approach to study the stability of logistic map [J]. Chaos， Solitons and Fractals， 2009， 41(4)： 2062-2066.

[15] 陳關榮， 汪小帆. 動力系統的混沌化-理論、方法及應用 [M]. 上海： 上海交通大學出版社， 2006： 88.

[16] 禹思敏. 混沌系統與混沌電路-原理、設計及其在通信中的應用 [M]. 西安： 西安電子科技大學出版社， 2011： 45.

責任編輯 陳呈超

Modified Logistic Map and Its Dynamic Performances

HAN Chun-Yan1，2，YU Si-Min1

(1. School of Automation，Guangdong University of Technology， Guangzhou 510006， China; 2. Department of Physics and Electronic Science， Binzhou University， Binzhou 256603， China)

In order to generate good chaotic pseudo-random sequences, we modified the Logistic map using scale transformation, constructing robust system and complex mapping respectively. Scale transformation for the Logistic map can arbitrarily expand its mapping region and chaotic range, improve stochastic characteristics and increase key space for its sequences. Constructing robust system will enable it to present constant chaos state with constant Lyapunov exponent, thereby forming a robust chaotic map. While complex map can increase its Lyapunov exponent by times and can improve its initial value sensitivity and randomness. Therefore, the modified Logistic map can be used as random sequence signal sources, which has application potential for secret communications, cryptosystems and computers.

chaos; Logistic map; robust chaotic map; complex map

國家自然科學基金項目(61172023； 61271064)；浙江省自然科學重點基金項目(LZ12F01001)；濱州學院科研基金項目(BZXYG1205)資助

2013-10-12；

2014-10-09

韓春艷(1973-)，女，副教授。E-mail:cyh660@163.com

O415.5

A

1672-5174(2015)05-120-06

10.16441/j.cnki.hdxb.20130447