一類強p-強制拋物型不等式中解的Liouville定理*

方鐘波， 徐麗君

(中國海洋大學數學科學學院，山東 青島 266100)

?

一類強p-強制拋物型不等式中解的Liouville定理*

方鐘波， 徐麗君

(中國海洋大學數學科學學院，山東 青島 266100)

研究一類具有奇異變系數的強p-強制擬線性拋物型不等式中解的非線性Liouville定理。通過適當構造試驗函數法來建立universal估計值(不依賴于初始值)，從而得出在適當的臨界指數范圍內非負非平凡整體弱解的非存在性結論。

強p-強制； 拋物型不等式； 試驗函數； Liouville定理

0 引言

本文考慮一類具有奇異系數的強p-強制擬線性拋物型不等式

ut-Lu≥a(x)uq,x∈Ω,t>0

(1)

具有初始條件

u(x,0)=u0(x),x∈Ω

(2)

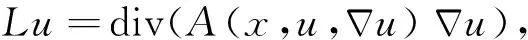
a(x)在邊界或原點具有奇性。所謂算子L為強p強制的(簡記為S-p-C)是指：如果存在常數c1,c2>0及p>1,使得對任意的(x,u,η)∈Ω×R×RN,

(3)

成立，如p-Laplace算子。

擬線性拋物型不等式(1)出現于流體力學、人口動力學及生物群體力學等諸多領域中，見文獻[1-3]等。從流體力學角度來說，描述多孔體介質中非牛頓滲流現象，可描述氣體或液體在多孔體介質中的流動，其中a(x)uq為正時叫“熱源”項，相反叫“冷源”項。

非線性拋物型方程(組)或不等式(組)中非負非平凡整體解的非存在問題的研究已有許多結論，見文獻[4-15]及相關文獻。1966年，Fujita在文獻[4]中研究半線性熱傳導方程的Cauchy問題

ut=Δum+V(x)uq,

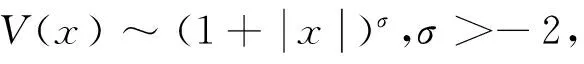
解的非線性Louville型定理。

由前述文獻所知，問題(1)～(2)中解的非線性Liouville定理的研究甚少。本文的目的在于利用試驗函數法問題(1)～(2)中得到強p-強制算子及加權函數的指數對非負非平凡整體弱解的非存在的影響，它的難點在于針對a(x)的不同奇性選取適當的試驗函數。此種方法是由Mitidieri和Pohozaev[16]中研究橢圓方程的時提出來的。它的優點在于推理簡單明了，不需要適應比較原理的一些假設，所以可以考慮類型廣泛的非線性方程。

1 預備知識及主要結論

先給出一些定義、記號及主要結論。因為p>1,強p強制拋物型不等式(1)可能為退化或奇異，所以一般不存在古典解，下面先給出弱解的定義。

定義1 如果非負函數u(x,t)滿足下面的條件：

(4)

則稱u(x,t)為問題(1)～(2)在S上的弱解。

關于a(x)的兩類奇性，討論以下兩種情形：

情形1 當Ω為有界區域時，a(x)在邊界?Ω附近具有奇性，此時

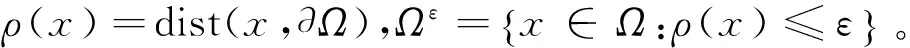
設存在c0>0,β∈R使得

a(x)≥c0ρ(x)-β,x∈Ω

(5)

情形2 當Ω=RN時，a(x)在原點附近有奇性，此時

假設

(6)

其中：c>0；β∈R。

下面按情形定義適當的試驗函數，將在證明主要結論中起到“鑰匙”作用。

和

(7)

和

(8)

令

χ(x)=ξλ

(9)

其中λ>0是一待定常數。

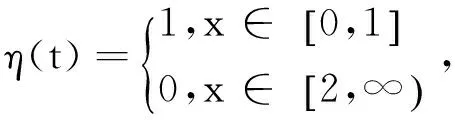
利用前面所構造的試驗函數，可得到如下形式的非線性Liouville定理。

(Ⅰ)當a(x)在邊界具有奇性時，

若上述條件成立，則問題(1)～(2)的解u(x,t)=0幾乎處處于S。

(Ⅱ)當a(x)在原點具有奇性時，

若上述條件(a)(b)之一成立,則問題(1)～(2)的解u(x,t)=0幾乎處處于S。其中θ為參數，r=q+1-p。

2 定理1的證明

定理1的證明主要分為3步。

步驟1 令T>0，定義QΩ,T且截斷函數定義為ψ(x,t)=ηT(t)χ(x),其中χ(x)如(2.6)所定義，ηT(t)=η(t/T)。

顯然有

取試驗函數Ψ=ψku-d，其中d=q-θ>0，k>1，并在QΩ,T上積分，可得

由(3)(即S-p-C)，可得

再由ψ(x,t)的定義得

(10)

對(10)的右端第一、二項應用Young不等式得

(11)

(12)

其中r=q+1-p。

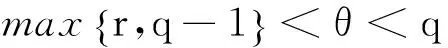
對(12)式右端第二項應用Young不等式得

(13)

結合(10)～(13)可得

則有

(14)

步驟2 當a(x)在邊界具有奇性時,

在(14)式中，取ξ=ξε，則有

(15)

(16)

再由(7)，(16)得

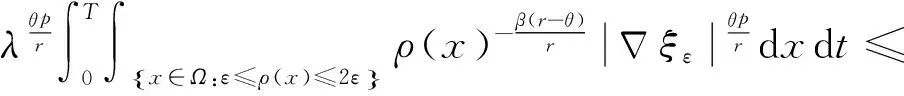
(17)

其中

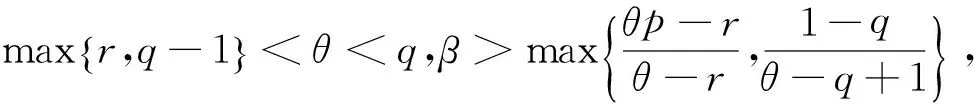
若上述條件成立，則有σ1>0，σ2>0，(17)式中取ε→0和T的任意性易知

即u(x,t)=0幾乎處處于S。

步驟3 當a(x)在原點具有奇性時，此時Ω=RN。

在(14)中取ξ=ξR，則有

(18)

由(6)，(18)可得

(19)

再由(8)，(19)得

(20)

其中

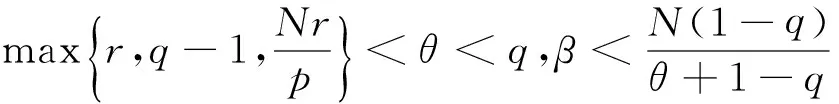
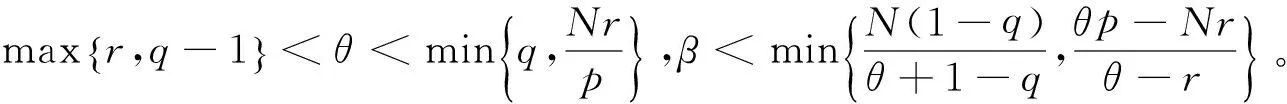
上述條件(a)(b)之一滿足，則有σ3<0，σ4<0。式(20)中取R→∞和T的任意性易知

即u(x,t)=0幾乎處處于S。

定理證畢。

[1] Bebernes J， Eberly D. Mathematical Problems from Combustion Theory [M]. New York： Springer， 1989.

[2] Samarskii A A, Galaktionov V A, Kurdyumov S P, et al. Blow-up in Quasilinear Parabolic Equationsde[M]. Berlin：Gruyter, 1995.

[3] Wu Z, Zhao J, Yin J. Nonlinear Diffusion Equations [M]. World Singapore: Scientific, 2001.

[4] Fujita H. On the blowing up of solutions to the Cauchy problem forRN[J]. J Fac Sci Univ Tokyo Sect 1A Math, 1966, 13: 119-124.

[5] Galaktionov V A, Vazquaez J L. Continuation of blowup solutions of nonlinear heat equations in several space dimensions [J]. Comm on Pure and Appl Mat, 1997, 50(1): 1-67.

[6] Kartsatos A G, Kurta V V. On the critical Fujita exponents for solutions of quasilinear parabolic inequalities [J]. Math Anal Appl, 2002, 269: 73-86.

[7] Piccirillo A M, Toscano L, Toscano S. Blow-up results for a class of first-order nonlinear evolution inequalities [J]. Differential Equations, 2005, 212: 319-350.

[8] 姜朝欣， 鄭斯寧. 一類雙重退化拋物型不等式問題解的Liouville型定理 [J]. 數學物理學報, 2010, 30A(3): 639-643.

[9] Mitidieri E, Pohozaev S I. Nonexistence of weak solutions for some degenerate elliptic and Parabolic problems onRN[J]. J evol equ 1, 2001(5)： 159-220.

[10] 魏公明. 具奇系數發展型p-laplace不等方程整體解的不存在性[J]. 數學年刊A輯, 2007, 28A(2): 387-394.

[11] Bandle C, Essen M. On positive solutions of Emden equations in cone-like domains[J]. Arch Rational Mech Anal,1990(4): 319-338.

[12] Laptev G G. Absence of solutions to semilinear parabolic differential inequalities in cones [J]. Mat Sb, 2001, 192: 51-70.

[13] Caristi G. Existence and nonexistence of global solutions of degenerate and singular parabolic systems [J]. Abstr Appl Anal, 2000(5): 265-284.

[14] Lian Songzhe, Liu Changchun. On the existence and nonexistence of global solutions for the porous medium equation with strongly nonlinear sources in a cone [J]. Arch Math, 2010, 94: 245-253.

[15] Fang Zhong Bo, Fu Chao, Zhang LinJie. Liouville theorems of slow diffusion differential inequalities with variable coefficients in cone[J]. J of KSIM, 2011, 15(1): 43-55.

[16] Mitidieri E, Pohozaev S I. Nonexistence of positive solution for quasilinear elliptic problems onRN[J]. Porc Stekxo Inst Math, 1999, 227: 192-222.

AMS Subject Classifications： 35R45; 35K65

責任編輯 陳呈超

Liouville Theorem of Solution for a Strongly-p-Coercive Parabolic Type Inequality

FANG Zhong-Bo，XU Li-Jun

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)

In this paper, we investigate the nonlinear Liouville type theorem of the strongly-p-coercive quasi-linear parabolic inequality with singular variable coefficients. By constructing appropriate test function to establish the universal estimate which does not depend on the initial value of solution, we obtain that the nonexistence of nonnegative nontrivial global weak solution in a range of appropriate critical exponent.

strongly-p-coercive; parabolic inequality; test function; Liouville theorem

山東省自然科學基金項目(ZR2012AM018)資助

2013-07-20；

2014-08-15

方鐘波(1968-)，男，教授。E-mail:fangzb7777@hotmail.com

O175

A

1672-5174(2015)05-126-05

10.16441/j.cnki.hdxb.20130257