涉及微分多項式和差分多項式的亞純函數的唯一性*

李效敏, 石 悅, 李 崗

(中國海洋大學數學科學學院，山東 青島 266100)

?

涉及微分多項式和差分多項式的亞純函數的唯一性*

李效敏, 石 悅, 李 崗

(中國海洋大學數學科學學院，山東 青島 266100)

應用差分Nevanlinna理論研究亞純函數及其移動算子或差分算子的1類非線性微分多項式分擔1個非零公共值的亞純函數的唯一性問題。本文結果部分回答了2009年方明亮提出的1個涉及微分多項式的亞純函數唯一性問題,推廣了Lahiri[6]、楊重駿和華歆厚[7]和方明亮[8]中的相應結果。

差分多項式； 微分多項式； 亞純函數； 唯一性定理

0 引言及主要結果

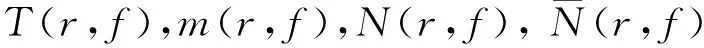
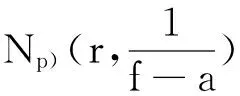
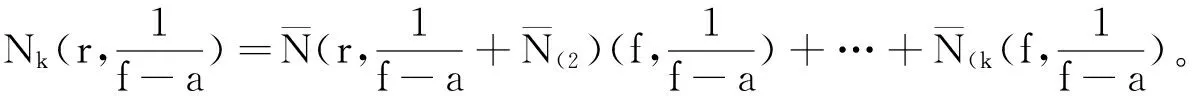
δ2(a,f)≤δ1(a,f)=Θ(a,f)≤1。

1976年,楊重駿提出了下述問題：

問題2[4]假設f與g是2個非常數的整函數，n是一個正整數。如果f與gCM分擔0，f(n)與g(n)CM分擔1，并且2δ(0,f)>1,那么f與g的關系如何？

1990年, 儀洪勛解決了問題2，證明了下述定理：

定理3[5]假設f與g是2個非常數的整函數，n是一個正整數。如果f與gCM分擔0，f(n)與g(n)CM分擔1，并且2δ(0,f)>1,那么f=g或者f(n)g(n)=1。

1997年,ILahiri提出了下述問題：

問題4[6]如果2個非常數的亞純函數的非線性微分多項式CM分擔1，那么這2個亞純函數的關系如何？

1997年,楊重駿和華歆厚研究了問題4，證明了下述定理：

定理5[7]假設f與g是2個非常數的亞純函數，n是1個正整數滿足n≥11。如果fnf'與gng'CM分擔1，那么f與g滿足下述2種情形之一：

(i)f=tg,其中t是1個常數，且滿足tn=1;

(ii)f=c1ecz,g=c2e-cz,其中c,c1和c2是非零常數，且滿足(c1c2)n+1c2=-1。

2002年，方明亮證明了下述結果，在整函數條件下研究了問題4，證明了下述定理：

定理6[8]假設f與g是2個非常數的整函數，n,k是2個正整數且滿足n≥2k+8。如果(fn(f-1))(k)與(gn(g-1))(k)CM分擔1，那么f=g。

2009年，方明亮在華東師范大學復分析會議上提出了下述問題：

問題7 假設f與g是2個非常數的亞純函數。n,k是2個正整數且滿足n>3k+11。如果(fn(f-1))(k)與(gn(g-1))(k)CM分擔1，那么是否有f=g？

截止到目前，問題7還沒有得到徹底解決。近幾年來RodneyHalburd-RistoKorhonen[13]以及馮紹繼與蔣翼邁[14]分別建立了差分Nevanlinna理論，ILaineandCCYang[15]得到了涉及差分多項式的Clunie定理。應用這些理論，一些芬蘭學者和中國學者開始了差分唯一性理論的研究，參看文獻[16-18]。 本文將利用差分Nevanlinna理論，結合微分多項式具有一個非零公共值的亞純函數唯一性問題的研究方法，研究一類差分微分多項式具有一個非零公共值的亞純函數的唯一性問題，具體說來，本文將研究下述幾個問題：

問題8 假設f(z)是1個非常數亞純函數，f(z+η)是f(z)的移動算子，其中η是1個非零復數，如果(fn(z)(f(z)-1))(k)與(fn(z+η)(f(z+η)-1))(k)CM分擔1，那么n,k在滿足什么條件下，有結論f(z)=f(z+η)？

問題9 假設f(z)是1個非常數的亞純函數，

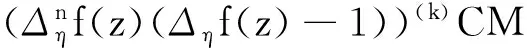
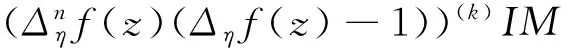
通過對上述幾個問題的研究，本文將證明下述幾個定理，從而回答了上述問題8～11。

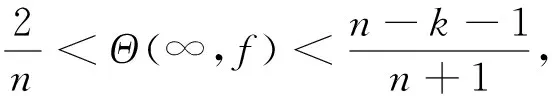
應用證明定理12和證明定理13的類似證明過程和本文第二部分引理10可得下述2個定理,它們分別是上述定理12和定理13的IM版本：

1 幾個引理

引理1[1]假設f是1個非常數的亞純函數，k是1個正整數，c≠0是1個有限值，那么

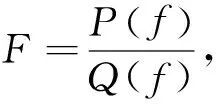
引理3 假設F是1個非常數的亞純函數，k,p是2個非常數的正整數，那么

引理4 假設f與g是2個非常數的亞純函數，n和k是2個正整數且滿足n>3k+11。如果(fn(f-1))(k)與(gn(g-1))(k)CM分擔1，并且f-1與g-1的每個零點重數≥k，那么

或者

證明 置

(1)

情形1 假設H不恒等于零。

設z0是(fn(z)(f(z)-1))(k)與(gn(z)(g(z)-1))(k)的1個公共單零點。 將(fn(z)(f(z)-1))(k)與(gn(z)(g(z)-1))(k)在z0點的Taylor展示代入(1)可知，z0是H的零點。于是再由(1)及引理4的條件可得

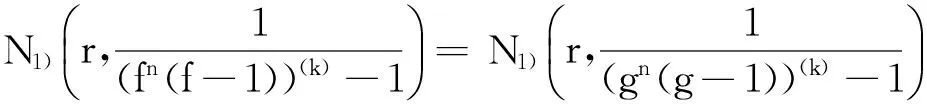
N(r,H)+m(r,H)+O(1)≤

(2)

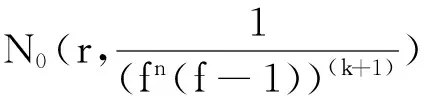
(n+1)T(r,f)+O(1)=T(r,fn(f-1))≤

S(r,fn(f-1))≤

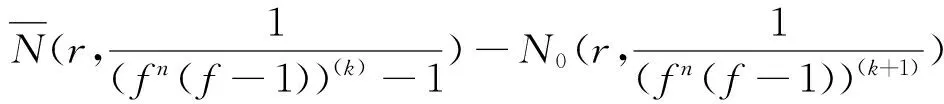
S(r,f),

即

(n+1)T(r,f)≤

S(r,f)。

(3)

同理

(n+1)T(r,g)≤

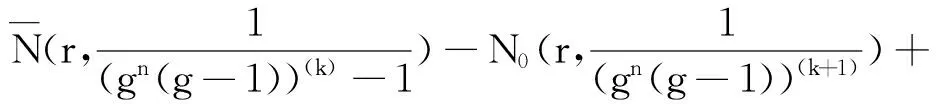
(4)

再由(2)和引理4的已知條件可得

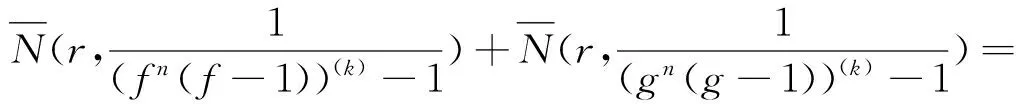
T(r,(fn(f-1))(k))+S(r,f)+S(r,g)≤

N(r,(fn(f-1))(k))+m(r,fn(f-1))+

S(r,f)+S(r,g)≤

S(r,f)+S(r,g)，

即

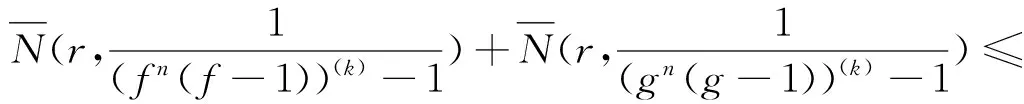
S(r,f)+S(r,g)。

(5)

將(5)代入(3)和(4)相加所得的不等式的右邊，并整理得

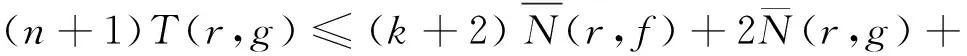
(6)

同理

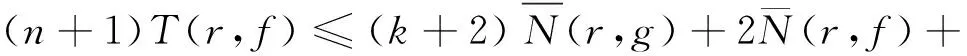
(7)

由(6)和(7)可得

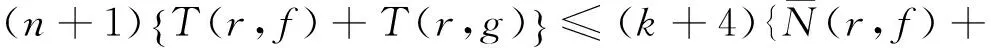
由此得n≤3k+11,這與已知條件n>3k+11矛盾。

情形2 假設H=0。由(1)可得

(8)

由(8)連續積分2次可得

(9)

其中a和b是2個常數,并且a≠0。分3種子情形討論如下：

子情形2.1 假設a=b。如果b=-1，由(9)可得(fn(f-1))(k)(gn(g-1))(k)=1，于是引理4的結論成立。

如果b≠-1，那么(9)可變為

(10)

由(10)可得

(11)

由(11)和引理1，引理2和引理3可得

(n+1)T(r,g)=T(r,gn(g-1))+O(1)≤

S(r,g)。

(12)

同理可得

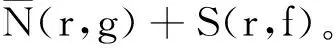
(13)

由(12)和(13)可得

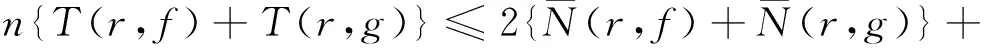
(2k+4){T(r,f)+T(r,g)}+S(r,f)+S(r,g)

由此可得n≤2k+4，這與已知條件n>3k+11矛盾。

子情形2.2 假設a≠b并且b≠0。

如果b=-1，那么(9)變為

(14)

由于(fn(f-1))(k)與(gn(g-1))(k)CM分擔1，由(14)可得

(n+1)T(r,g)=T(r,gn(g-1))+O(1)≤

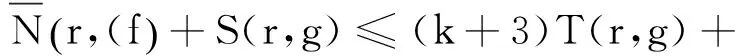
T(r,f)+S(r,g)，

于是

(15)

另一方面，再將(14)改寫成

(16)

由(16)和引理3可得

(n+1)T(r,f)=T(r,fn(f-1))+O(1)≤

(k+3)T(r,f)+(k+3)T(r,g)+S(r,f)，

于是

(n-k-2)T(r,f)≤(k+3)T(r,g)+S(r,f)

(17)

由(15),(17)和條件n>3k+11可得矛盾。

如果b≠-1，那么(9)變為

(18)

由(18)，類似于(14)條件下的推導過程可得矛盾。

子情形2.3 假設a≠b并且b=0。由(9)可得

a(fn(f-1))(k)=(gn(g-1))(k)

(19)

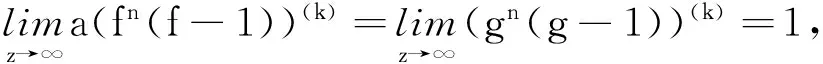
以下假設當f,g是2個超越亞純函數。一方面，由(19)可得：

a(fn(f-1))(k)=(gn(g-1))(k)+P1

(20)

其中P1是1個次數不超過k的多項式。假設P1不恒等于零，由(20)和引理2可得

a(fn(f-1))(k)=(gn(g-1))(k)+P1

(21)

和

(n+1)T(r,f)=T(r,fn(f-1))+O(1)≤

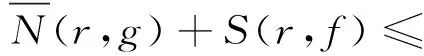
(k+3)T(r,f)+(k+3)T(r,g)+S(r,f)

(22)

由(21)和(22)可得n≤2k+5，這與n>3k+11矛盾。于是P1=0，(20)變為afn=gn，由此得

a(fn(f-1))(k)=(gn(g-1))(k)

(23)

另外，由前面得到的(3)可得

(24)

由(24)可知(fn)(k)-1有零點。注意到a(fn(f-1))(k)與(gn(g-1))(k)CM分擔1，由(23)可知a=1，于是引理4成立。引理4證畢。

引理5[13-14](對數導數引理的差分模擬)假設f是1個非常數亞純函數，并且其增長級滿足ρ(f)=ρ<∞，η≠0是復常數，則對任意正數ε，有

引理6[14,Theorem2.1]假設f是1個非常數亞純函數，并且其增長級滿足ρ(f)=ρ<∞，η≠0是復常數，則對任意正數ε，當r充分大時，有

T(r,f(z+η))=T(r,f(z))+O(rρ-1+ε)。

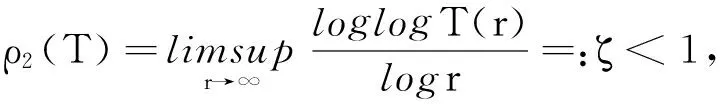
引理8 假設f1和f2是2個非常數亞純函數，且滿足f1+f2=1，那么

引理9[12]假設s>0和t是是2個互素的整數，c是1個滿足cs=1的復數，那么ωs-1與ωt-c有且只有1個公共零點。

引理10[19]假設f與g是2個非常數亞純函數，k≥1是1個正整數，并且f(k)與g(k)IM分擔1。如果Δ1= (2k+3)Θ(∞,f)+(2k+4)Θ(∞,g)+Θ(∞,f)+

Θ(∞,g)+2δk+1(0,f)+3δk+1(0,g)>4k+13

和Δ2= (2k+3)Θ(∞,g)+(2k+4)Θ(∞,f)+Θ(∞,g)+

Θ(∞,f)+2δk+1(0,g)+3δk+1(0,f)>4k+13

成立，那么f(k)g(k)=1或者f=g。

2 定理的證明

定理13的證明 設f(z+η)-f(z)=g(z)。由引理4，分2種情形討論如下：

情形1 假設

[f(z)n(f(z)-1)](k)
[(f(z+η)-f(z))n(f(z+η)-f(z)-1)](k)≡`1

(25)

首先,(fn(f-1))(k)不恒等于常數。事實上，若(fn(f-1))(k)恒等于某個常數，那么

fn(f-1)=Pk

(26)

其中Pk是某個次數≤k的多項式。注意到f是1個非常數的亞純函數，并且n>3k+11，無論f是有理函數還是超越亞純函數，都可以由(26)和引理2得出矛盾。于是，由(25)可知

[(f(z+η)-f(z))n(f(z+η)-f(z)-1)](k)也不恒等于常數。 以下假設z0是f(z)的p≥1重極點，那么z0一定是[(f(z+η)-f(z))n(f(z+η)-f(z)-1)](k)的零點，從而z0也是f(z+η)的p重極點。于是由(25)和引理3，5和6可得

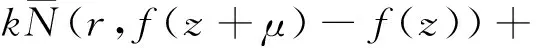
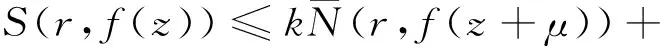
(k+1)T(r,f(z+η)-f(z))+

T(r,f(z+η)-f(z)-1)+S(r,f(z))≤

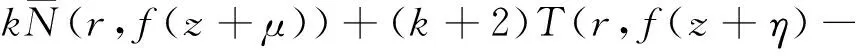
(k+2)[m(r,f(z+η)-f(z))+N(r,f(z+η))]+

S(r.f(z))≤

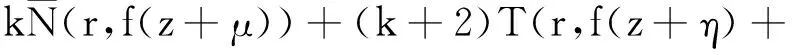
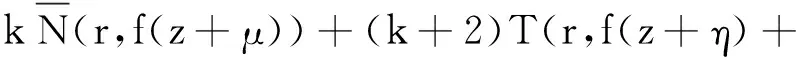
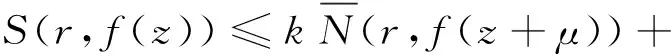
(k+2)T(r,f(z)+S(r,f(z))

(27)

注意到f(z)的增長級ρ(f)<∞，由引理7可得

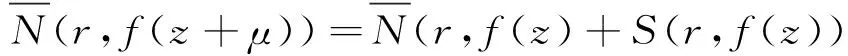
(28)

由(27)和(28)可得

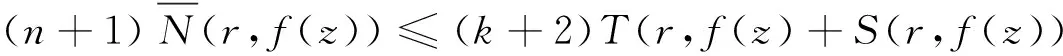
(29)

情形2 假設

(fn(f-1))(k)=(gn(g-1))(k)

(30)

其中

g(z)=f(z+η)-f(z)

(31)

由(30)可得

fn(f-1)-gn(g-1)=Qk

(32)

其中Qk是1個次數不超過k的多項式。如果Qk不恒為零，由(32)，引理2和引理8可得

和

(n+1)T(r,f)=T(r,fn(f-1))+o(1)≤

該式與n>3k+11矛盾。所以Qk=0，于是(32)變為

fn(f-1)=gn(g-1)

(33)

以下假設f不恒等于g。設

(34)

以下分兩種子情形討論：

子情形2.1 假設h是1個常數，那么h≠1，于是1-hn+1和1-hn+1不同時為零。由(33)和(34)可得(1-hn+1)g=1-hn，于是(1-hn+1)(1-hn)≠0，從而

(35)

這與g為非常數的亞純函數矛盾。

子情形2.2 假設h不恒為常數，那么h-1，1-hn+1和1-hn全不恒為零，于是由(33)和(34)可得(35)。由引理9可知，1-ωn+1和1-ωn有且只有1個公共零點ω=1。由此結合(35)和引理2可得

(36)

于是S(r,f)=S(r,h)。由第二基本定理可得

(n-2)T(r,h)+S(r,h)，

(37)

其中，αj(1≤j≤n)是ωn+1=1的n個判別的根并且αj≠1。于是由(37)可得

這與已知條件Θ(∞,f)>2/n矛盾。于是f=g，即f=Δηf。從而完成了定理13的證明。

定理12的證明 由引理4,分2種情形討論如下：

情形1 假設

(38)

首先類似于定理13證明過程中的情形1可得(fn(f-1))(k)和(f(z+η)n(f(z+η)-1))(k)均不恒為常數。再由(38)，引理3，引理5和引理6可得

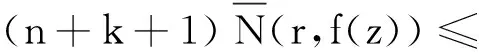
N(r,f(z)n(f(z)-1)](k))=

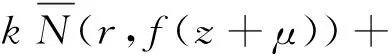
(k+1)T(r,f(z+η))+T(r,f(z+η)-1)+

(k+2)T(r,f(z+η))+S(r,f(z))≤

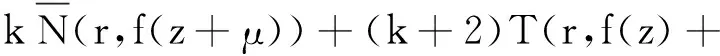
S(r,f(z))

(39)

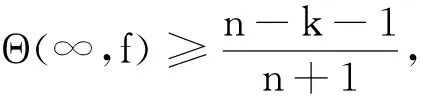
情形2 假設

(40)

由(40)，類似于定理13的證明過程中情形2可得f(z)=(f(z+η)，于是完成了定理12的證明。

致謝：本文作者感謝審稿人有價值的評論和建議。

[1]HaymanWK.Meromorphicfunctions[M].Oxford：TheClaredon， 1964.

[2] 儀洪勛， 楊重駿. 亞純函數的唯一性理論 [M]. 北京： 科學出版社， 1995.

[3]LahiriI.Weightedsharingofthreevaluesanduniquenessofmeromorphicfunctions[J].KodaiMathJ2011， 24(3)： 421-435.

[4]YangCC.Ontwoentirefunctionswhichtogetherwiththeirderivativeshavethesamezeros[J].JMathAnalAppl, 1976, 56：1-6.

[5]YiHX,UniquenessofmeromorphicfunctionsandaquestionofC.C.Yang[J].ComplexVarTheoryAppl, 1990, 14(1)： 169-176.

[6]LahiriI.Uniquenessofmeromorphicfunctionsasgovernedbytheirdifferentialpolynomials[J].YokohamaMathJ， 1997,44(2)： 147-156.

[7]YangCC，HuaXH.Uniquenessandvalue-sharingofmeromorphicfunctions[J].AnnAcadSciFennMath， 1997, 22 ： 395-406.

[8]FangML.Uniquenessandvaluesharingofentirefunctions[J].ComputMathAppl， 2002( 44)：5-6, 823-831.

[9]Mokhon’koAZ.OntheNevanlinnacharacteristicsofsomemeromorphicfunctions[M]//TheoryofFunctions,FunctionalAnalysisandTheirApplications,kovsk:Izd-voKhar’kovsk.Un-ta, 1971: 83-87.

[10]LahiriI,SarkarA.Uniquenessofameromorphicfunctionanditsderivative[J].JInequalPureApplMath， 2004， 5(1)： 20.

[11]FrankG.EineVermutungvonHaymanübernullstellenmeromorpherFunktion[J].MathZ, 1976,149(1)： 29-36.

[12]ZhangQC.Meromorphicfunctionssharingthreevalues[J].IndianJpureapplMath, 1999, 30(7): 667-682.

[13]HalburdR,KorhonenR,TohgeK.Holomorphiccurveswithshift-invarianthyperplanepreimages[J].TransAmerMathSoc, 2014, 366(8): 4267-4298.

[14]ChiangYM，FengSJ.OntheNevanlinnacharacteristicoff(z+η) and difference equations in the complex plane [J]. Ramanujan J, 2008(16)： 105-129.

[15] Laine I, Yang C C. Clunie theorems for difference and q-difference polynomials [J]. J London Math Soc, 2007, 76(1): 556-566.

[16] Heittokangas J, Korhonen R, Laine I, et al. Value sharing results for shifts of meromorphic functions and sufficient conditions for periodicity [J]. J Math Anal Appl, 2009, 355(1): 352-363.

[17] Heittokangas J, Korhonen R, Laine I, et al. Uniqueness of meromorphic functions sharing values with their shifts [J]. Complex Var Elliptic Equ， 2011, 56(1-4)： 81-92.

[18] Zhang J L. Value distribution and shared sets of differences of meromorphic functions [J]. J Math Anal Appl, 2010, 367(2): 401-408.

[19] Li X M, Yi H X. Uniqueness of meromorphic functions whose certain nonlinear differential polynomials share a polynomial [J]. Comput Math Appl， 2011, 62(2): 539-550.

AMS Subject Classifications： 30D30; 30D35

責任編輯 陳呈超

(fn(f-1))(k)(gn(g-1))(k)=1

(fn(f-1))(k)=(gn(g-1))(k)。

(n-k-2)T(r,g)≤T(r,f)+S(r,g)

(f(z)n(f(z)-1))(k)(f(z+η)n(f(z+η)-1))(k)≡1

(f(z)n(f(z)-1))(k)=(f(z+η)n(f(z+η)-1))(k)

Uniqueness Results Concerning Differential Polynomials and Difference Polynomials of Meromorphic Functions

LI Xiao-Min, SHI Yue, LI Gang

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)

Using the difference Nevanlinna theory, we study the uniqueness questions of meromorphic functions whose certain nonlinear differential polynomials share one nonzero finite value with the same of the shifts or the difference operators of the meromorphic functions. The results in the present paper partly give an answer to a question concerning nonlinear differential polynomials of meromorphic functions which was posed by M. L. Fang in 2009. The results in the present paper also extend the corresponding results as in Lahiri[6]、Yang-Hua[7]and Fang[8].

defferential polynomials; difference polynomials; meromorphic functions; Uniqueness theorems

國家自然科學基金項目(11171184；40776006);國家自然科學基金中俄合作協定項目(10911120056);山東省自然科學基金項目(Z2008A01; ZR2009AM008)資助。

2013-05-29；

2014-07-12

李效敏(1967-)，男,副教授。E-mail: xmli01267@gmail.com

O174.52

A

1672-5174(2015)05-131-08

10.16441/j.cnki.hdxb.20130247