一類特殊三角函數的最大值解

周桂如

（福建船政交通職業學院基礎教研室，福建福州350007）

一類特殊三角函數的最大值解

周桂如

（福建船政交通職業學院基礎教研室，福建福州350007）

首先在△ABC中，給出特定系數的最大值問題，分別利用逐步分析法、拉格朗日乘數法和不等式三種方法獲得相同的結果，然后利用拉格朗日乘數法推導出任意系數三角函數（其中）的最大值求解方法，最后推導三角函數（其中）的極值。

拉格朗日乘數法；逐步分析法；極值

引言

最值和不等式，是數學組成的重要內容和部分，不等式揭示變量之間的制約關系，而最值問題與它緊密相關。三角函數的最值問題是函數最值問題的一個重要部分。解答三角函數的最值問題，除了要用到代數中求最值問題的定理和方法外，通常還要借助三角函數的一些特性來求解。

引理1[1]：，當其中時取得最大值。

引理2[2]：在任意△ABC中有

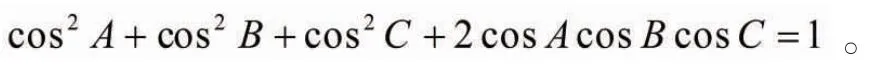
引理3[3]：對及及任意△ABC有當且僅當且時等號成立。

引理4[4]：設函數在點的某鄰域內具有二階連續偏導數，且點是函數的駐點，即，記：則：

1 主要結果

1.1 逐步分析法[5]

三角形三個角A、B、C的取值范圍為

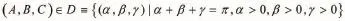
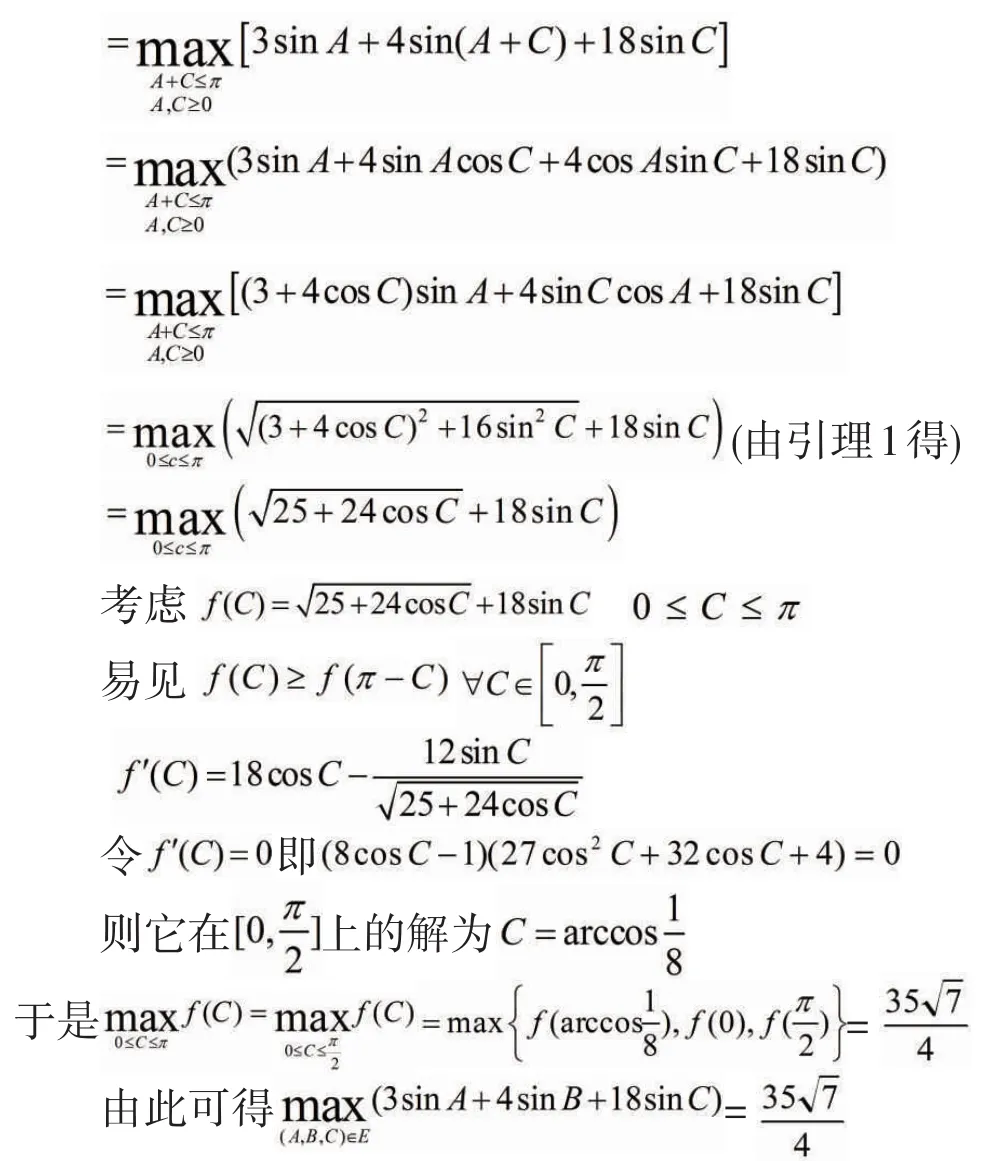
1.2 用拉格朗日乘數法

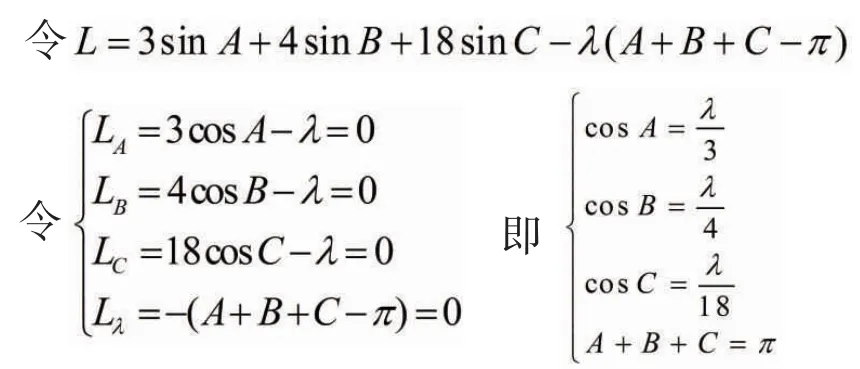
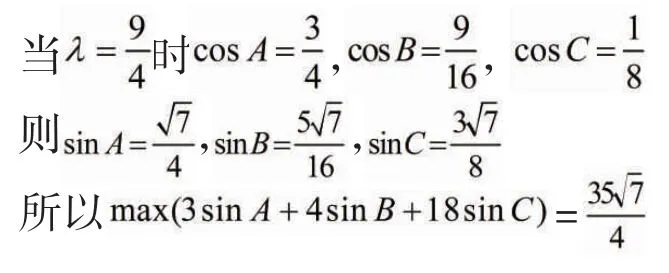
1.3 不等式法

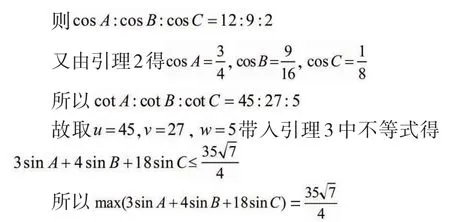
2 一般形式的三角函數極值

2.1 對于△ABC，（其中）的極值

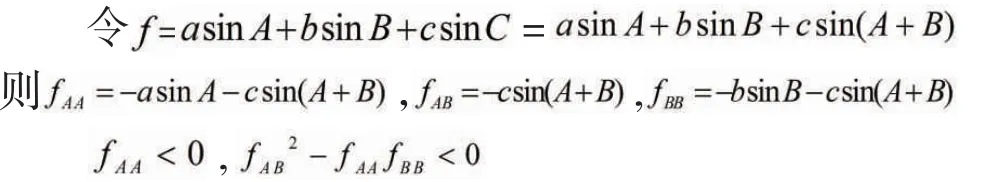
根據拉格朗日乘數法

2.2 對于△ABC，（其中的極值

根據拉格朗日乘數法

3 結語

三角函數最值問題題型豐富多彩，其解法也層出不窮。例如利用三角函數的有界性、換元法、判別式法、利用函數的單調性、對含參數的三角函數最值的分類討論法、利用基本不等式法（如：和差化積與積化和差公式、均值不等式、柯西不等式）等都是解三角函數最值的常用手段,解決這類問題關鍵是在于對三角函數的靈活應用，抓住關鍵和本質所在。

注釋及參考文獻：

[1]數學教材研究開發中心．普通高中課程標準實驗教科書[M]．北京：人民教育出版社，2004：35-40．

[2]裴禮文．數學分析中的典型問題與方法[M]．北京:高等教育出版社,1993,267-287．

[3]楊學枝．關于三角形的兩類不等式[J]．湖南教育學院學報，1999,17(2):32-37．

[4]華東師范大學數學系．數學分析第三版[M]．北京:高等教育出版社,2003．

[5]胡中雙．淺談高中數學教學中創造性思維能力的培養[J]．湖南教育學院學報，2001,19(4):147-148．

The Solution to Maximum Value of a Special Class of Trigonometric Functions

ZHOU Gui-ru
（Department of Basic Teaching,Fujian Chuanzheng Communications College,Fuzhou，Fujian 350007）

For the maximum value of a trigonometric functionwith special coefficients in△ ABC,three solutions of analysis segment,the Lagrange multiplier,the inequalities,are first proposed,leading to the same result.Then for a general trigonometric functionwith the coefficients,b,andcbelonging to，the Lagrange multiplier is used to seek its maximum value.Finally,the solution to the extreme value of the trigonometric functionwith the coefficients,b,andcbelonging tois derived.

Lagrange multiplier;analysis segment;extreme value

O174

A

1673-1891（2015）03-0012-03

2015-05-03

周桂如（1980-），女，碩士，講師，主要從事應用數學方面的研究。