一種基于泛函極值的等周約束問題的求解方法

吳群妹

(無錫科技職業學院，江蘇無錫214000)

一種基于泛函極值的等周約束問題的求解方法

吳群妹

(無錫科技職業學院，江蘇無錫214000)

等周約束問題實質上是一個帶積分方程約束的泛函極值問題。利用泛函極值的基本定理求解出等周約束問題，方便快捷。

泛函變分;泛函極值;等周問題

引言

等周問題最早是由著名數學家Joham Beynoulli在1697年提出的,即在具有定長的一切平面單純閉曲線中,圓是最大面積的曲線[1]。此后,很多學者都對這個問題展開了討論與研究[2-3]，有《平面等周問題的兩個推廣形式》[4]、《含約束條件的等周問題的研究》等等。變分法是17世紀末開始發展起來的一個數學分支,是為了研究泛函的極值問題而產生的。而“等周約束問題”實質就是一個帶積分方程約束的泛函極值問題。本文根據變分法的基本定理,將帶積分方程約束的極值問題轉化為帶微分方程的泛函極值問題對“等周約束問題”的建立了模型,并且求出其解。

1 等周問題

等周問題的描述如下:在平面上長度一定的所有封閉光滑曲線中找一條曲線,使其所圍成的面積最大。下面先對“等周問題”建立數學模型。

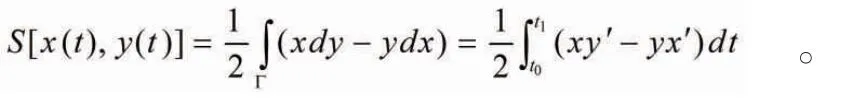
于是等周問題歸結為在封閉光滑曲線的集合

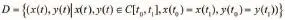
2 變分法基本原理

帶積分方程約束的泛函極值問題具有以下定理:

定理1[5]設是具有一階連續導數的維向量函數，是標量函數,且相對于其所有的自變量都具有連續的一階和二階偏導數，是所有的自變量都具有連續一階和二階偏導數的維向量函數。求使泛函取得極值且滿足等周約束條件和固定邊界條件、的極值軌線，其中是維常向量。解決這個問題的思路是引進新的變量,將積分方程約束變量轉化成微分方程的約束條件。令，則新變量滿足條件，并且。這樣帶積分方程約束的泛函極值問題轉化為帶微分方程約束的泛函極值問題。構造Lagrange函數如下:

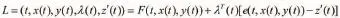
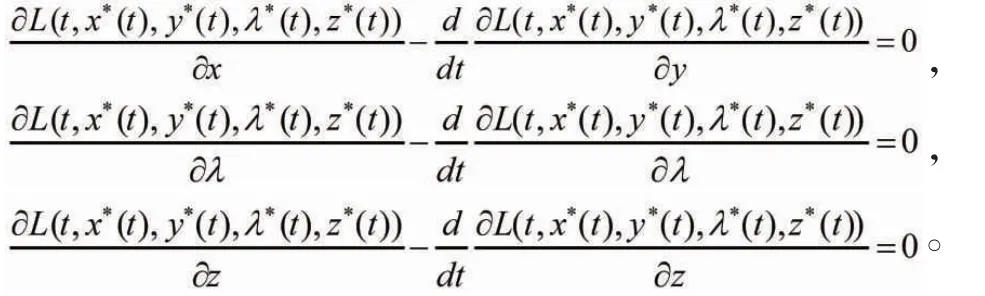
定理2[5]設是具有一階連續導數的維向量函數，是標量函數,且相對于其所有的自變量都具有連續的一階和二階偏導數，是所有的自變量都具有連續一階和二階偏導數的維向量函數。使泛函取得極值且滿足等固約束條件和固定邊界條件、的最優軌線應滿足的必要條件為

3 基于泛函極值的等周約束問題的求解

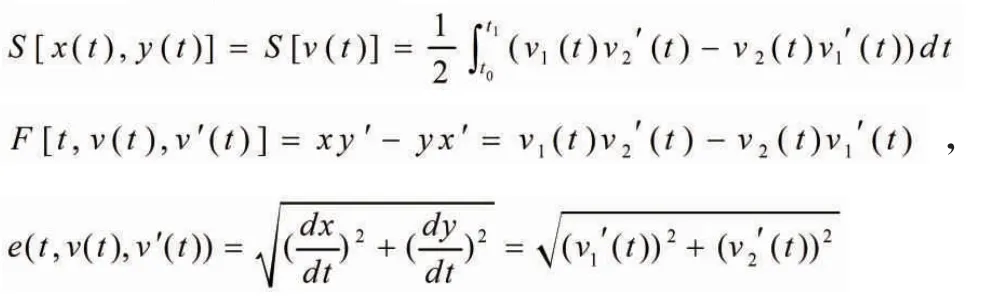
4 小結

本文利用變分法中帶積分約束泛函的極值問題很好的求解了積分約束的等周問題。此外,等周問題還有《分數階導數的等周問題》[6],《兩平行線間的等周問題》[7]等,今后將會對其他形式的等周問題作進一步探討。

注釋及參考文獻：

[1]項武義．等周問題的一個初等證明[J]．數學年刊,2002（23A）：7-12．

[2]孫冬梅．變分法在求解最速渡江路線問題的應用[J]．高等數學研究,2005,8(6),55-59．

[3]姬小龍．關于等周問題級數解法的一些改進[J]．大學數學,2005,21(2)：82-83．

[4]劉鵬．平面等周問題的兩個推廣形式[J]．高等函授學報(自然科學版),2009,22(4)：76-77．

[5]張蓮,胡曉倩,王彬,等．現代控制理論[M]．北京:清華大學出版社,2008：314-323．

[6]高正暉,楊柳,劉剛．一類含分數階導數的等周變分問題[J]．衡陽師范學院學報，2014,35(6)：1-4．

[7]劉海亭,李壽貴,柴方．限制在兩平行線間的等周問題[J]．數學雜志,2012,32(2)：377-380．

ASolution Method Based on Functional Extremum of Isoperimetric Problem

WU Qun-mei
(Wuxi Technology and Professional College,Wuxi，Jiangsu 214000)

The isoperimetric constraint problem is essentially a functional extrema of integral equations with constraints.It is convenient to use the basic theorems of functional extremum solving the isoperimetric constraint problem.

functional variation;functional extreme;isoperimetric problem

O177.92；O176.2

A

1673-1891（2015）03-0015-02

2015-05-11

吳群妹(1981-),女，江蘇蘇州人,碩士研究生,講師,主要從事高等數學、應用數學、最優控制研究。