榫卯式滿堂支撐體系承載力試驗及非線性后屈曲分析

劉 杰 何小涌，* 劉 群 趙海瑞

(1．天津大學建筑工程學院，天津300072;2．中國建筑科學研究院，北京100013;3．天津迅安嘉會建材技術有限公司，天津300457)

1 引言

腳手架作為一種臨時結構不僅需要能夠承擔包括施工器械、建筑材料、模板及工人在內的豎向荷載，還要能夠承擔風荷載、沖擊荷載、地震荷載這樣的水平荷載［1］。也許正是作為一種臨時結構，其結構的重要性及安全性才會被工程師所忽略，因此我們能夠頻頻聽到有關腳手架坍塌安全事故的報道［2］。目前市場上擁有品類眾多的腳手架并且都有各自的特點，然而頻發的腳手架坍塌事故呼吁我們尋求一種更加安全、合理、經濟的承載體系。在尋求合理的承載體系時，同樣需要尋求更加安全的分析設計理論用以指導工程實踐并避免重大安全事故。因此，本文將介紹采用古代木結構最常見的榫卯式連接的新型腳手架承載體系。該新型榫卯式支撐腳手架目前在國內還沒有工程應用實例，至今沒有相關的試驗研究，為了說明此體系的合理性及承載性能，做了11個8．05 m超高腳手架原型試驗并基于試驗分析結果進行了極限荷載的非線性后屈曲分析。

2 榫卯式支撐體系簡介

榫卯式支撐腳手架的設計靈感來源于榫卯結構，繼承結構的科學適用性，充分利用現代新材料，通過現代化的設計加工，把剛性連接和柔性連接相結合，使其承載力和安全性達到較高的水平。各個構件之間的結點以榫卯相接合，構成富有彈性的框架，其結構體系有外觀簡潔、施工速度快、周轉壽命長等優點。下面對該體系的節點連接、豎桿搭接及頂部構造做相關介紹。

圖1給出了該體系的節點連接方式。

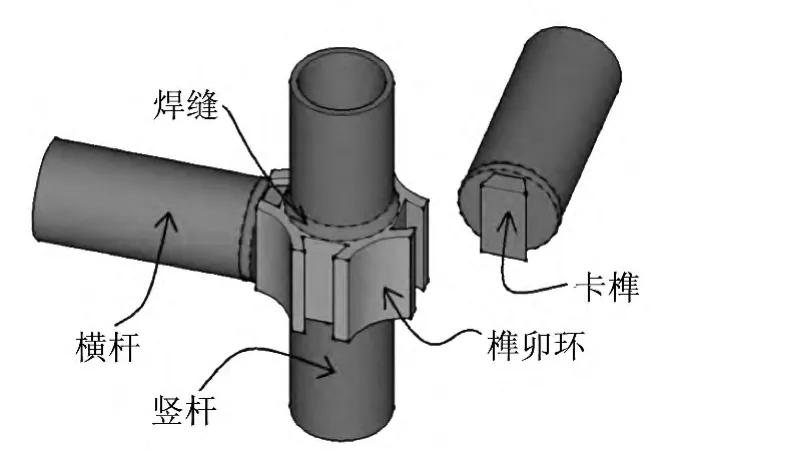
圖1 節點模型Fig．1 Joint model

榫卯環每隔0．6 m被角焊縫可靠地連接在豎桿上，卡榫采用對接焊縫連接在長度為0．6 m、0．9 m、1．2 m的橫桿兩端。楔形卡榫置于楔形榫槽中并適當敲擊就會牢固地結合在一起。豎桿搭接方式如圖2所示，套管內徑略大于豎桿外徑的無縫鋼管采用角焊縫連接于豎桿，這樣增加了連接可靠性、保證豎桿連續變形。頂部承載方式如圖3所示，頂托可通過螺紋固定在豎桿內部，頂托上可放置木枋或水平圓鋼管承擔模板傳遞的載荷。

圖2 套管搭接圖Fig．2 Spigot joint

圖3 頂托Fig．3 U-head

3 承載力試驗研究

3．1 加載裝置

圖4給出了試驗加載示意圖:4個反力架牢固地被地腳螺栓連接于地梁上;每個反力梁下放置2個量程為500 kN的千斤頂，共計8個;千斤頂下放置兩根6 m長分配梁，可以使載荷均勻地分配給I20a工字鋼。圖5給出了處于工作狀態下的千斤頂實物圖，整套裝置傳力路徑如下:

(1)反力路徑:千斤頂→大梁→立柱→地梁。

(2)加載路徑:千斤頂→分配梁→工字鋼→通長橫桿→頂托→支撐體系。

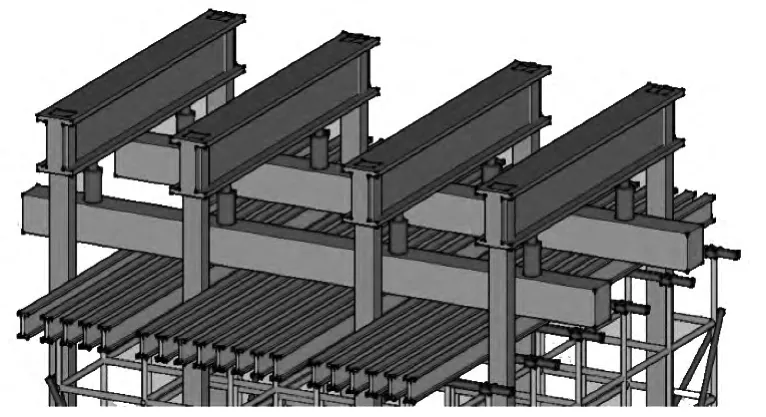
圖4 加載示意圖Fig．4 Loading schematic diagram

圖5 千斤頂布置圖Fig．5 Set up of lifting jack

3．2 傳感器布置

試驗準備階段首先采用液壓萬能試驗機對千斤頂和液壓傳感器及油壓表的對應關系做了標定，因此載荷的大小通過油壓表或液壓傳感器的讀數換算得到，油泵及油壓表見圖6。

圖6 油壓表Fig．6 Oil pressure gauge

如圖7所示，位移傳感器被固定于萬向表座以保持水平;限于篇幅，這里只給出試驗8、試驗9的位移傳感器布置圖。如圖8所示，在東、北立面分別布置3個位移傳感器，可以測出各測點水平位移。這樣布置目的有兩個:

(1)可以得出水平位移隨加載的變化規律;

(2)豎向不同位置的位移可以反映加載裝置對試驗架頂部的約束作用，可指導后續有限元分析邊界條件的確定。

該超高支撐體系失穩破壞時兩個主要現象為中部水平位移突變及油壓表讀數持續下降，因此停止加載標準為:在本級荷載下位移傳感器讀數發生突變并且油壓表讀數降幅高于上一級荷載的20%，這時取上一級荷載為破壞荷載。

圖7 位移傳感器Fig．7 Displacement sensor

圖8 位移傳感器布置Fig．8 Setup of displacement sensor

3．3 搭設參數

由于該新型榫卯支撐體系承載力較高，至今為止還未研發與之配套的剪刀撐構件以提高整體承載力;為了能夠更全面、更深入地了解該體系的承載能力，不僅研究了橫桿間距、立桿步距對整體承載力的影響，還采用扣件式豎向剪刀撐對該體系進行加固并研究其對承載力的影響。如圖9所示，架體四周各搭設扣件式剪刀撐，剪刀撐采用旋轉扣件與豎桿扣接。表1給出了11個足尺支撐體系的搭設參數。

3．4 試驗結果及分析

3．4．1 承載力分析

表2給出了極限承載力試驗結果，并簡要分析有無剪刀撐對極限承載力的影響，由表2可以得出如下結論:

圖9 剪刀撐搭設形式Fig．9 Set up of X-bracing

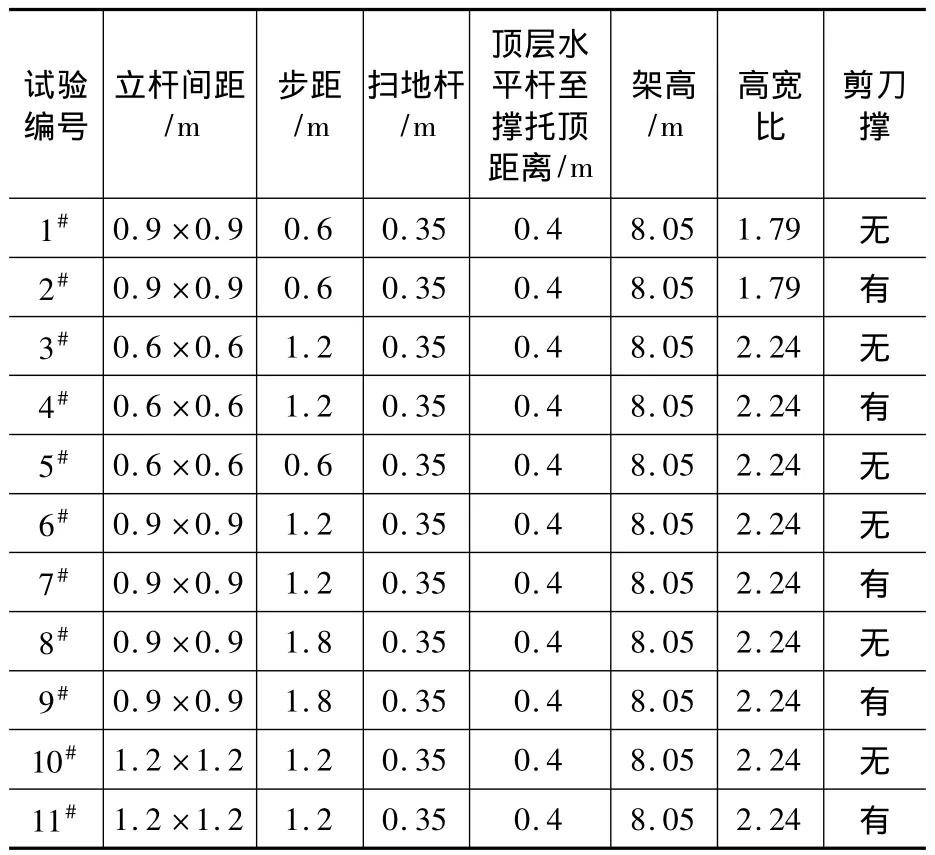
表1 搭設參數Table 1 Geometric parameters

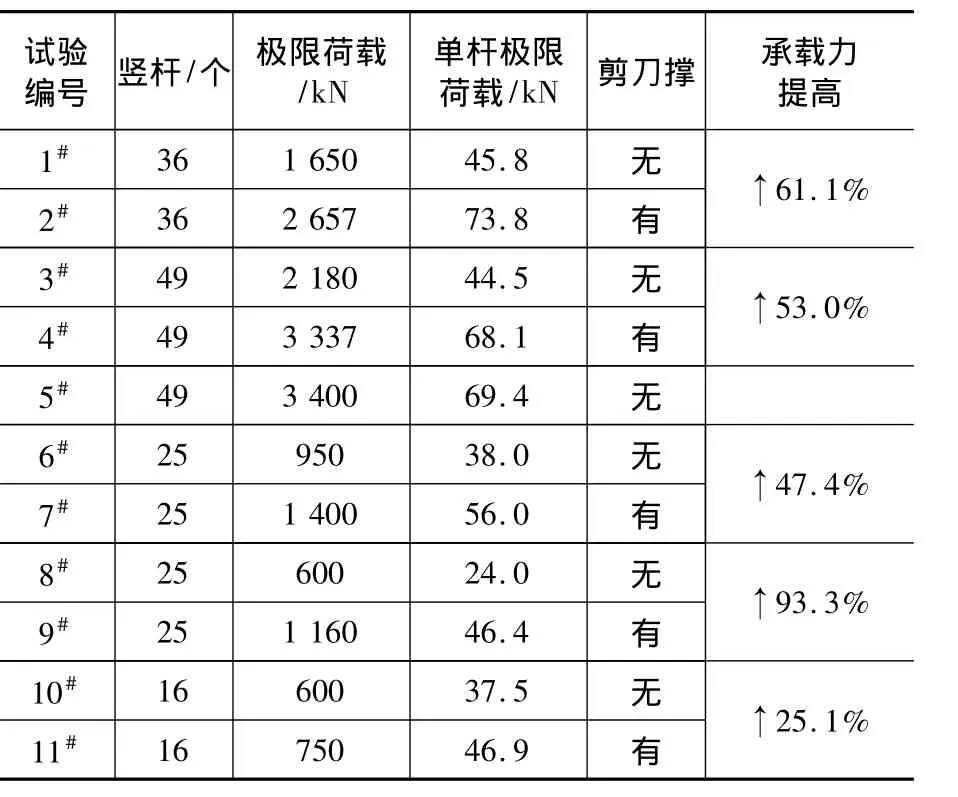
表2 承載力試驗結果Table 2 Bearing capacity of experiment

(1)增加剪刀撐可以顯著提高支撐體系的豎向承載力，其承載力提高25% ～93%。

(2)增加剪刀撐后承載力提高幅度不盡相同，說明不同搭設參數對有無剪刀撐的敏感性很大;在設計或施工中應該注意該特性，避免過高或者過低估計支撐體系的承載力。

(3)試驗9比試驗8承載力提高近一倍，說明具有試驗8搭設參數的支撐體系對有無剪刀撐的敏感性很大;可以推斷:由于該節點的半剛性特征，不適于搭設步距達到甚至超過1．8 m。

表3給出了在不搭設剪刀撐的情況下，橫桿步距、立桿間距對豎向承載力的影響，由表3可以得出如下結論:

(1)立桿間距不變，橫桿步距每減少600 mm，承載力提高8～25kN。

(2)橫桿步距不變，立桿間距減小300 mm或600 mm，體系承載力提高7～25kN。

表3 無剪刀撐時承載力對比Table 3 Bearing capacity comparison without X-bracing

表4分析了有剪刀撐的情形，橫桿步距、立桿間距對體系豎向承載力的影響，由此可以得出如下結論:

(1)立桿間距不變，橫桿步距每減少600 mm，豎向承載力能提高10 kN左右;

(2)橫桿步距不變，立桿每減少300 mm，豎向承載力能提高10 kN左右，變化較均勻。

3．4．2 位移分析

圖10—圖12分別給出了試驗1、試驗5、試驗7各位移測點處水平位移隨荷載變化的規律曲線;由于測點3與測點6位于支撐體系底部且水平位移基本為零，因此未在圖中給出測點3、測點6的測試結果。根據位移荷載曲線可以得出如下結論:

表4 有剪刀撐時承載力對比Table 4 Bearing capacity comparison with X-bracing

圖10 試驗1位移荷載曲線Fig．10 Displacement-load curve of 1#

圖11 試驗5位移荷載曲線Fig．11 Displacement-load curve of 5#

(1)架體中部位移測點2、測點5比相同立面頂部測點1、測點4位移較大，說明結構失穩模態接近一階失穩，雖然各階模態都和變形有關但是一階變形貢獻最大;

(2)各架體都表現出雙向一階失穩，但是不同架體不同方向變形比例不同:試驗5表現為一個方向的失穩變形遠大于另一個方向失穩變形，試驗1、試驗7卻表現出雙向失穩，兩個方向的失穩變形都很大;

(3)結構在最后一、二級荷載下測點位移突變，說明了結構失穩喪失承載能力具有突發性及不可預見性;

(4)試驗1中測點5，試驗5中測點2、測點4及試驗7中測點5在加載開始與結尾的位移異號，說明隨著荷載的增加，架體由于各種缺陷的影響，其失穩方向不一定是初始變形方向，失穩方向在結構失穩之前不可預見。

圖12 試驗7位移荷載曲線Fig．12 Displacement-load curve of 7#

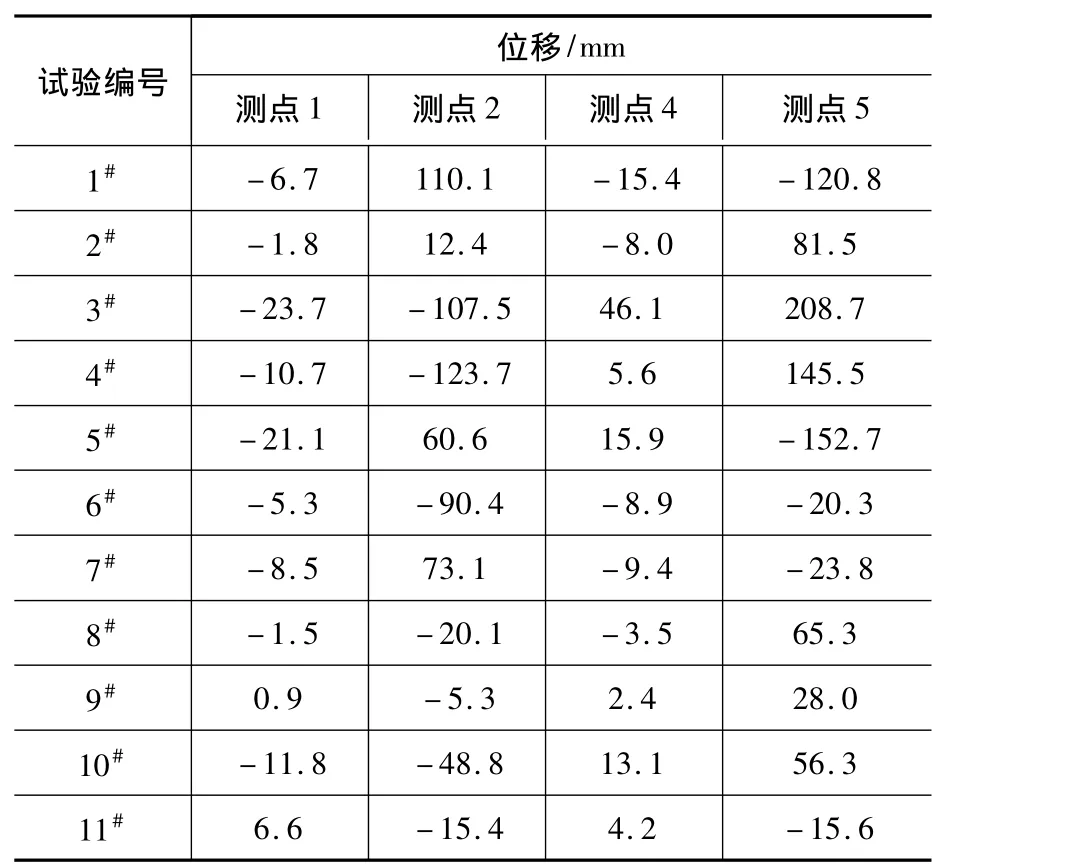
表5 試驗水平位移Table 5Horizontal displacement of experiment

從表5中可以看出結構達到極限承載力時所呈現的破壞形態，頂部水平位移明顯小于體系中部水平位移，由此可以推斷結構呈現出弓形失穩模態，后續給出的試驗照片也說明了結構失穩形態。表5中結構頂部位移遠小于中部位移說明體系并不是頂部自由、可側向偏移的邊界條件，因此后續有限元分析中可以采用頂部鉸接;當然頂部鉸接給了結構過量的約束，由于試驗中很難評估反力架對體系的水平約束力，在有限元分析中只有適當增加初始缺陷以抵消鉸接對結構產生的過約束效應。由表中測點位移數據還可以推算出兩個方向失穩模態的比例，為后續有限元分析初始缺陷的引進提供參考。

3．4．3 試驗現象

圖13、圖14分別展示了搭設和未搭設扣件式剪刀撐時支撐體系達到極限承載力時的變形圖，從圖中可以看出支撐體系呈弓形失穩模態，從表5各測點位移可以得出同樣的結論。

圖13 試驗1Fig．13 Picture of 1#

圖14 試驗4Fig．14 Picture of 4#

圖15 展示了支撐體系失穩破壞時連接剪刀撐與豎桿的扣件的破壞形態，此時扣件鑄鐵材質的脆性及較大的變形導致了扣件的崩裂破壞。

圖16給出了節點的破壞形態，常見的節點破壞形式是左圖，當整個體系呈弓形失穩時變形最大的部位常常出現此類節點破壞，此類破壞特點由榫卯節點特性決定。右圖的破壞形式不常見，整個試驗過程中只發現3個此類型節點破壞模式;此類卡榫脫離榫槽的現象屬小概率事件，出現的原因大致可歸于施工操作不當及局部變形過大這兩個因素。

圖15 剪刀撐破壞形式Fig．15 Failure mode for X-bracing

圖16 節點破壞形式Fig．16 Failure mode for joints

4 非線性屈曲分析

含幾何非線性的靜力問題有時會出現屈曲和坍塌這樣的極值點失穩問題，這時荷載－位移響應會表現出負剛度特性并且結構需要釋放應變能來保持平衡［3］。若要獲得完整的荷載位移曲線，必須在模型中引入初始缺陷，這樣ABAQUS就能采用弧長法分析出如圖17所示完整的荷載—位移曲線，由此獲得結構的極限承載力。

4．1 節點轉動剛度

文獻［4］對扣件式腳手架中直角扣件的抗彎剛度進行了詳盡的試驗研究，但是在有限元模型中采用了彎矩－轉角曲線的原點切線剛度，本文在ABAQUS軟件的*SPRING模塊中定義完整的彎矩－轉角試驗曲線以考慮轉動剛度隨荷載的非線性響應。本文將對比分析節點剛接與節點半剛性的分析結果，為保證單一因子變量，模型中將采用相同的材料非線性、初始缺陷比例及邊界條件。圖18給出了試驗加載裝置實物照片，圖19給出了3個試件的彎矩－轉角曲線。

圖17 荷載－位移曲線Fig．17 Load-displacement curve

圖18 轉動剛度試驗裝置Fig．18 Setup for torsion stiffness test

圖19 彎矩－轉角試驗曲線Fig．19 Test curve of moment-curvatur

4．2 材料非線性

試驗裝置如圖20所示，本文將強度等級為Q235的鋼管加工為弧長10 mm、標距為50 mm的3個試樣進行了拉伸試驗;從圖21可以看出3個試樣的拉伸曲線較為接近，這表明了鋼管材質較為均勻。

圖20 拉伸試驗裝置Fig．20 Setup for tensile test

圖21 應力－應變曲線Fig．21 Curve of stress-strain

文獻［5］在腳手架整體分析模型中采用了理想彈塑性的鋼材本構關系，在模型中僅僅輸入了彈性模量、泊松比及屈服強度卻沒有考慮材料的強化階段。為了讓有限元分析能夠與試驗結果具有可比性，首先根據式(1)推導出真實應力與塑性應變的對應關系，其次在有限元模型中輸入真實應力與塑形應變兩列數據，并不需要人為輸入彈性模量、屈服強度及抗拉強度。

式中，σnom，σ分別對應名義應力和真實應力;εnom，ε，εpl分別對應名義應變、真實應變及塑性應變。

4．3 初始缺陷

結構的幾何缺陷在荷載作用下會產生二階效應，包括:①桿件弓形彎曲會產生 P－δ效應;②框架整體偏移在分析中會產生P－Δ效應。目前初始缺陷的引進方法［6－9］大致有以下三種:

(1)特征屈曲模態比例法:先對結構進行屈曲模態分析，然后在原模型上疊加一定比例的最低階模態或者某幾階模態。

(2)名義水平力法:在構件上引進水平力模擬桿件弓形彎曲和結構的整體偏移。

(3)直接引進初始幾何缺陷法:當結構幾何缺陷的具體值是已知的時候，可以直接定義節點坐標。

在ABAQUS軟件的*IMPERFECTION模塊中引進初始缺陷主要包括模態數的確定和各模態的比例。本文首先完成各模型的特征值屈曲分析，其次參考表5中各測點的試驗值大致確定了體系的失穩模態及兩個方向失穩模態的比例，在后屈曲分析中引入相應的模態及雙向失穩比例。

4．4 邊界條件

邊界條件影響著結構的剛度，因此也就影響著屈曲模態的分析。模型中較精確的邊界條件可以使有限元分析結果更加接近試驗結果;反之，則可能使分析結果與試驗結果相差甚遠。從相關文獻［10］及本文的加載裝置圖可知，支撐體系頂部加載時，結構頂部也會受到由于摩擦及豎向壓力而產生的水平約束力。由于支撐體系所受豎向壓力一般很大，通常試驗加載能達到幾十噸甚至數百噸，因此加載裝置對支撐體系的頂部約束不能忽略。在工程實踐中支撐體系承受模板自重、混凝土自重及施工作業所產生的豎向荷載，由這些荷載及摩擦產生的約束必定會阻止水平向的變形。

本文有限元模型的邊界條件為豎桿底部采用完全固接、頂部采用僅豎向自由的約束方式，具體分析見3．4．2中有關位移分析得出的相應結論。

4．5 數值分析結果及對比

4．5．1 承載力對比

表6給出了數值計算結果并與試驗結果進行了對比，從中可以得出以下結論:

(1)不論是采用節點剛性還是節點半剛性模型，豎向剪刀撐對支撐體系的極限承載力影響規律沒有發生變化;

(2)根據試驗結果確定的節點半剛性模型的分析結果和試驗很接近，二者誤差在2 kN以內，說明根據試驗結果建立有限元分析模型思路是可行和有效的;

(3)節點剛性分析模型過高地估計了支撐體系的極限承載力，誤差在25 kN以內，這在實際工程上是偏于不安全的，由此說明有必要建立更加準確的分析模型。

表6 數值與試驗承載力對比Table 6 Bearing capacity comprarison betwwen FEM and test

4．5．2 位移對比

由表5知體系失穩破壞時會出現圖22所示的變形:當頂部與中部位移同號時出現左圖情形，反之異號時出現右圖情形。

圖22 彎曲值示意圖Fig．22 Schematic diagram of bending value

由于有限元模型中采用了底部固接、頂部僅豎向可滑動的邊界條件，本文主要對比了支撐體系失穩時豎桿的弓形彎曲值。圖中彎曲值S可由幾何知識求得，半剛性有限元模型與試驗對比結果如表7所示，從表中可知試驗與有限元分析的豎桿彎曲值比較接近且誤差在10%以內，說明了有限元模型的有效性及采用彎曲值對比方法的合理性。

表7 數值與試驗彎曲值對比Table 7 Bending value comparison between FEM and test

4．5．3 荷載位移曲線

采用RIKS分析極限承載力得出的荷載－位移曲線如圖23、圖24所示:圖23是節點剛性模型得出的荷載－位移曲線，當達到極限承載力后荷載下降迅速，結構表現出很大的剛度，失穩具有瞬時性并表現為脆性破壞;圖24是節點半剛性模型分析出的荷載－位移曲線，當達到極限荷載后承載力雖有所下降但下降速度很慢，表現出一定的延性。

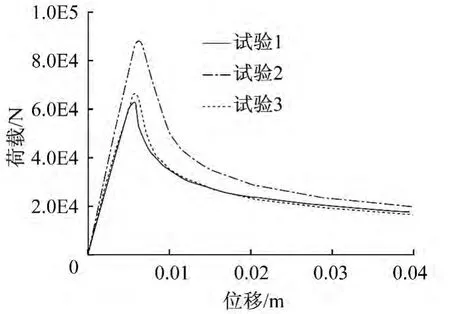
圖23 節點剛性Fig．23 Rigid joints

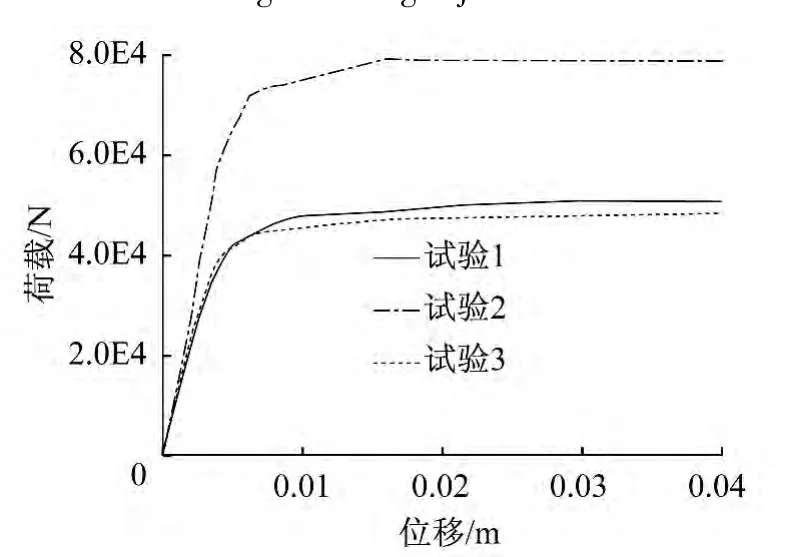
圖24 節點半剛性Fig．24 Semi-rigid joints

圖25 、圖26分別給出了不設剪刀撐和搭設剪刀撐的典型失穩模式，與試驗所觀測到的失穩模式相同:不搭設剪刀撐的體系呈現弓形大波鼓曲破壞，而搭設剪刀撐的體系變形最大處應該在體系高度約1/4及3/4處。

圖25 試驗1的失效模式Fig．25 Failure mode of 1#

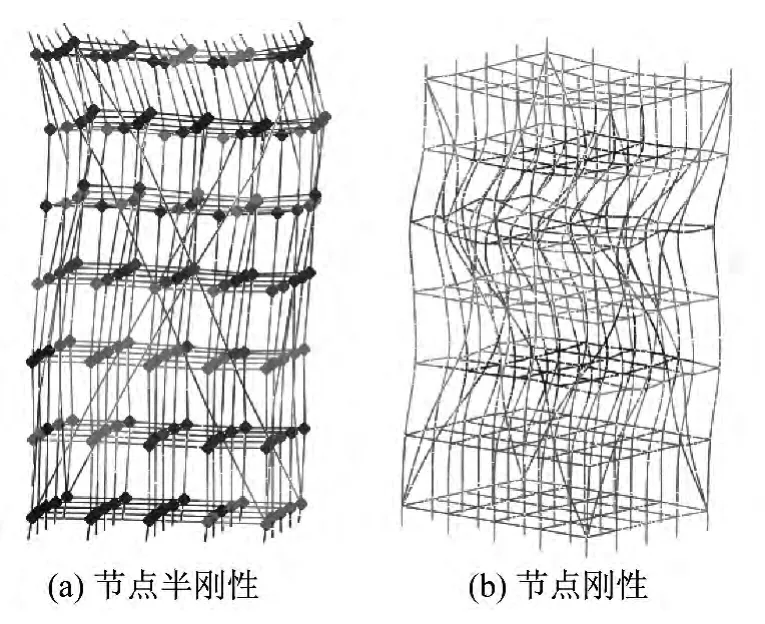
圖26 試驗7的失效模式Fig．26 Failure mode of 7#

5 結論

(1)為較全面地研究新型榫卯式超高滿堂支撐體系的豎向承載力性能進行了11套足尺原型試驗，并在試驗結果的基礎上建立包括材料非線性、幾何非線性、初始缺陷、節點半剛性的相對精細化的有限元分析模型。節點半剛性模型和試驗結論吻合較好，然而節點剛性模型承載力比試驗結果高約20 kN，對工程實際偏于不安全。

(2)不搭設剪刀撐時，橫桿步距、立桿間距能夠明顯提高體系的承載力;采用扣件式剪刀撐能夠明顯改善支撐體系剛度和承載力，此時步距、間距提高極限承載力的幅度大致相同。

(3)支撐體系的極限承載力并對比了有限元分析得出的荷載－位移曲線，結果表明:節點剛性模型在達到極限承載力后荷載急劇下降表現出失穩的突然性，符合脆性破壞的概念;節點半剛性模型達到極限承載力后荷載隨位移變化較平緩，符合延性破壞的特征。

(4)在分析模型中引進基于試驗位移結果而確定的失穩模式及各方向的失穩比例，這種建模思路能夠更好地使有限元分析反映試驗結果。

［1］ Chandrangsu T，Rasmussen K J R．Structural modeling of support scaffold systems［J］．Journal of Constructional Steel Research，2011，67(5):866-875．

［2］ 鄭屹峰．建筑施工腳手架安全事故分析［D］．長沙:中南大學，2010．Zhang Yifeng．Analysis of safety events of construction scaffoding［D］．Changsha:Central South University，2010．(in Chinese)

［3］ Dassault Systèmes Simulia Corp． Abaqus version 6．11，Analysis user’s manual［M］．2011．

［4］ 袁雪霞，金偉良，魯征，等．扣件式鋼管支模架穩定承載能力研究［J］．土木工程學報，2006，05:43-50．Yuan Xuexia，Jin Weiliang，Lu Zheng，et al．A study on the stability bearing capacity of fastener-style tubular steel formwork-supports［J］．China Civil Engineering Journal，2006，05:43-50(in Chinese)

［5］ 陸征然，陳志華，王小盾，等．扣件式鋼管滿堂支撐體系穩定性的有限元分析及試驗研究［J］．土木工程學報，2012，01:49-60．Lu Zhengran，Chen Zhihua，Wang Xiaodun，et al．Experimental and theoretical study of the bearing capacity of fastener steel tube full-hall formwork support system［J］．China Civil Engineering Journal，2012，01:49-60(in Chinese)

［6］ Chan S L，Zhou Z H，Chen W F，et al．Stability analysis scaffolding semi-rigid steel scaffolding［J］．Engineering Structures，1995，17(8):568-574．

［7］ 楊應華，王燕．軸心受壓蜂窩鋼柱的穩定性能分析［J］．結構工程師，2013，05:52-58．Yang Yinghua，Wang Yan．Stability analysis of concentrically compressed cellular steel columns［J］．Structural Engineers，2013，05:52-58(in Chinese)

［8］ Yu W K，Chung K F，Chan S L．Structural instability of multi-storey door-type modular steel scaffolds［J］．Engineering Structures，2004，26(7):867-881．

［9］ Chan S，Huang H，Fang L．Advanced analysis of imperfect portal frames with semi-rigid base connections［J］．Journal of Engineering Mechanics，2005，131(6):638-640．

［10］ 陸征然．扣件式鋼管滿堂支承體系理論分析與試驗研究［D］．天津:天津大學，2010．Lu Zhengran．Experimental and theoretical study on fastener steel tube full formnork support system［D］．Tianjin:Tianjin University，2010．(in Chinese)