山地底部不等高柱框架結構側向剛度計算方法

王麗萍，李英民，韓軍

(1.重慶科技學院建筑工程學院，重慶401331;2.重慶大學土木工程學院，重慶400045)

隨著城市建設用地的日益減少，人們環保意識及與自然環境相融合的人居環境要求的提高，國內外一些城市逐漸開始興建與山地地形及自然環境相適應的山地房屋。歷次震害及研究表明［1-12］，底部不等高柱架空的山地建筑結構，在強震作用下易于發生不期望的破壞模式，如柱端過早的剪切破壞。這是由于實際工程中山地結構底層常常被設計為柱截面相同而柱高不等的結構形式，以致無法避免出現底層柱剛度和強度難以合理匹配的問題。強震中當底層短柱柱端已發生剪切破壞時，其他相對較高柱由于分擔的剪力較少還未達到或接近屈服，結構整體已經傾斜從而引發倒塌。因此，推遲短柱發生破壞的時間，在彈性階段控制盡管計算機可以完成結構的精確計算，但簡化手算方法是結構工程師永遠不能缺少的必備知識，也是分析結構受力機理和判斷機算結果合理性的重要途徑。D值法是目前計算多、高層框架在水平荷載作用下的內力應用最廣泛的一種近似計算方法。此方法是基于假設同層柱高相同且柱端節點轉角相同的條件下推導而得，如果當柱高不同，即使層側移相同，柱端節點轉角(θ)及柱底旋轉角(φ=Δ/h)也會不同。那么，當D值法運用于底層不等高柱山地框架結構時，其適用性和準確性有待進一步考證。目前相關研究較少，文獻［13］只是針對這一問題進行探討，并未給出合理的解決方法。本文將基于矩陣位移法典型方程進行力學推導，通過在剛度修正系數(α)中考慮柱端節點轉角和不等高柱旋轉角差異的影響，研究適用于底部不等高柱山地框架結構的側向剛度計算方法，以便掌握其內力分布規律［15-18］。

1 Muto＇s D值法驗證

1922年Tachu Naito首先提出了D值法，此方法是基于假設同層柱高相同且柱端節點轉角相同的條件下推導而得，由于僅考慮了柱截面對剛度的影響，從而導致計算誤差較大。于是1955年Muto通過考慮梁柱線剛度比的影響修正了D值法，對于同層柱高相等情況此修正方法計算結果較為準確。對于同層柱高不等時，Muto通過柱高比的平方再次修正剛度系數［14］:

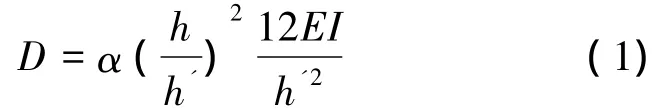
式中:h為相鄰的相對較高柱子高度，h'為相鄰的相對較短柱子高度，α為考慮梁柱線剛度比的剛度修正系數。

為考察Muto＇s D值法的準確程度，本文分別采用Muto＇s D值法與有限元方法對相同結構進行計算結果對比。算例基本設計信息:單跨單層不等高框架結構，跨度6 m，梁截面均為250 mm× 550 mm，柱截面均為550 mm×550 mm，設底層柱高比為η=h1/h2(h1和h2分別表示相鄰柱高)，取η=1～3，左側頂點加水平集中力為1 000 kN。采用通用有限元軟件Sap2000建模計算，其剪力和剛度計算結果可看成是精確解。定義δk為剛度相對誤差，δv為剪力相對誤差:

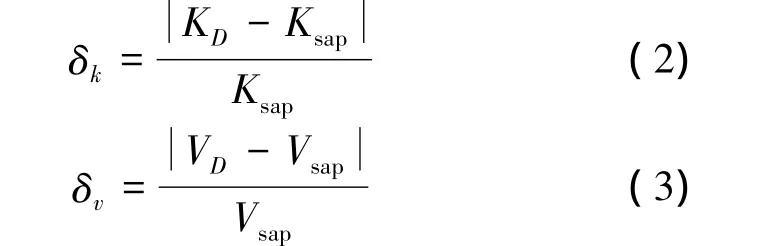
式中:KD和VD分別為采用Muto’s D值法計算的柱剛度和剪力，Ksap和Vsap為分別采用SAP2000計算的柱剛度和剪力。

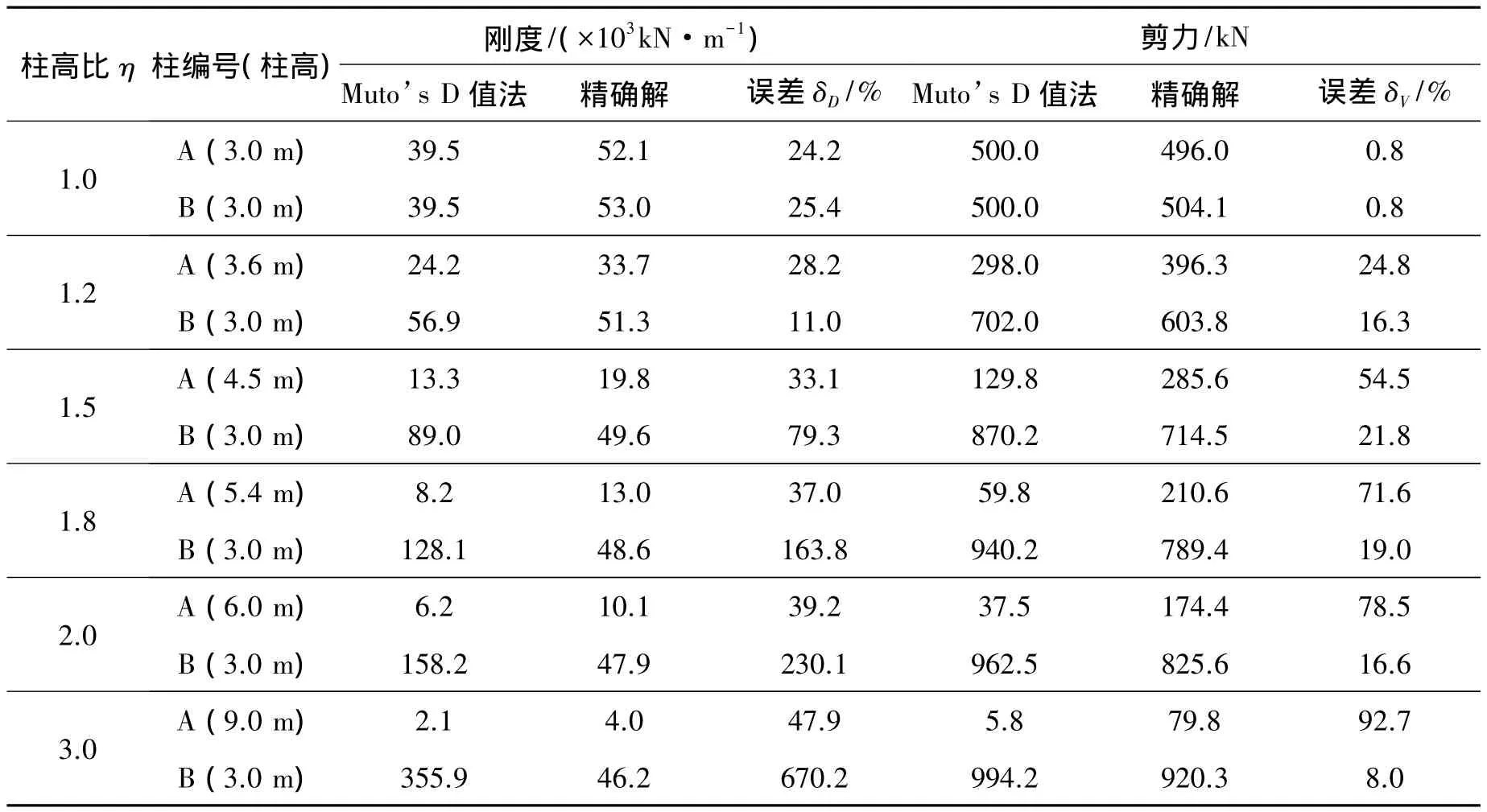
表1 Muto’s D值法計算誤差對比Table 1 The comparison of calculation error by Muto’s D method

從表1中可以看出，對于底層等高的普通框架結構采用Muto’s D值法計算的柱剛度比實際柱剛度偏小，但是通過Muto’s D值法求得剪力相對誤差很小，這是因為通過Muto’s D值法計算柱剛度再計算剪力分配系數，在剪力分配系數中弱化了剛度誤差帶來的影響，從而使得通過Muto’s D值法計算剪力值誤差較小。但是，當柱高比值η在不斷增加時，無論剛度相對誤差還是剪力相對誤差都在逐漸增大，剛度最大誤差達到670.2%，剪力最大誤差達到92.7%。因此，對于底層不等高框架結構在計算柱剛度和剪力時Muto’s D值法已經不能滿足精度要求，為避免誤差過大和增強D值法在底層不等高柱框架中的適用性需要對D值進行修正。

2 底部不等高柱框架結構側向剛度計算方法

2.1 單跨不等高柱側向剛度計算方法推導

建立單層單跨不等高框架模型如圖1所示。基本假設及其說明如下:1)材料服從胡克定律，即材料的線彈性假設;2)構件在外力作用下所產生的變形與構件尺寸相比都很小，即小變形假設;3)構件以彎曲變形為主，不考慮構件的軸向變形和剪切變形;4)每根構件均為等截面直桿，其截面屬性在構件長度方向不發生改變。

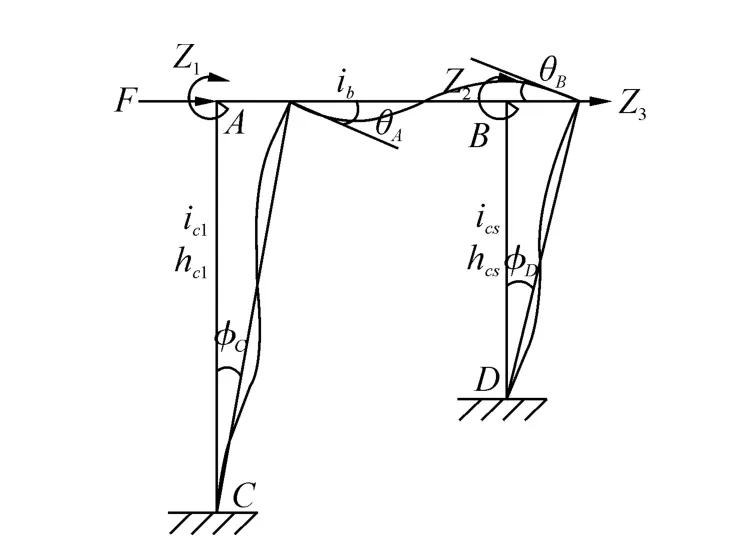
圖1 單跨不等高柱框架模型Fig.1 The single-span model with uneven ground column heights

假設1和假設2保證結構分析中的疊加原理成立;假設3和假設4確定了構件的變形能力并減少了結構力學位移法計算的獨立自由度數。通過以上的4條基本假設，如圖1所示單層單跨結構獨立自由度數3個，分別為AC柱端節點轉角Z1、BD柱端節點轉角Z2和AB梁端側向位移Z3，iAB、iAC、iBD分布表示梁 AB和柱 AC、BD的線剛度。在A點施加水平側向力F，可建立位移法典型方程:

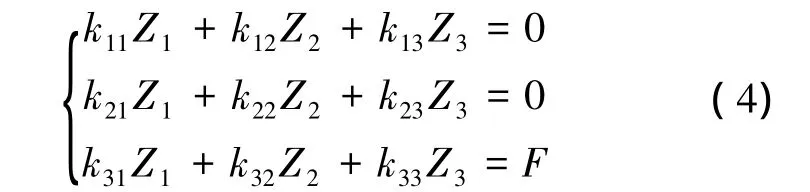
式中:kij表示附加約束j單獨發生單位位移Zj=1時在附加約束i處產生的約束反力。根據反力互等定理，k12=k21，k13=k31，k23=k32，將方程(4)改寫為矩陣形式:

化簡為

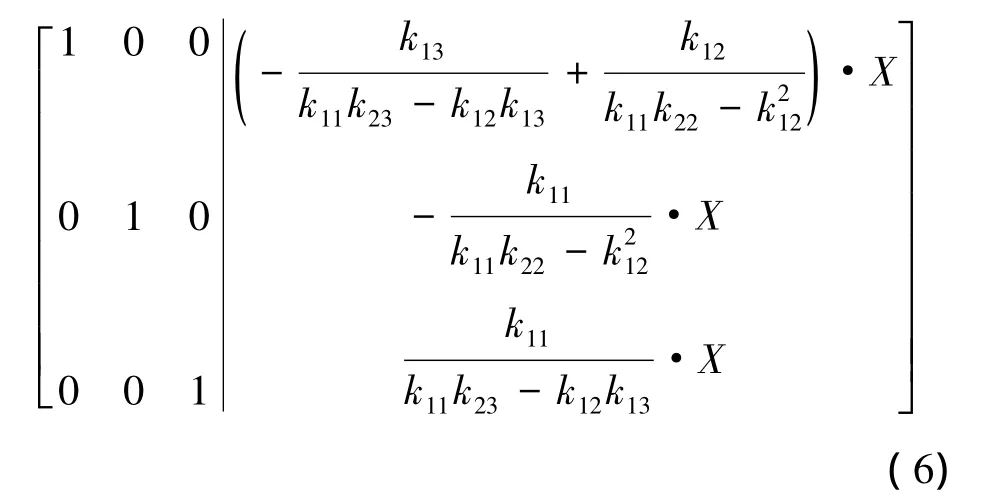
最終，位移表達式為

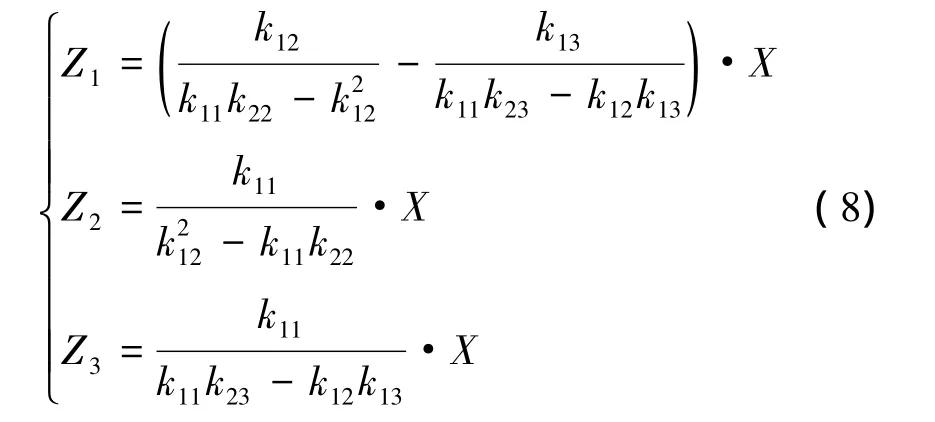
根據結構力學位移法可得

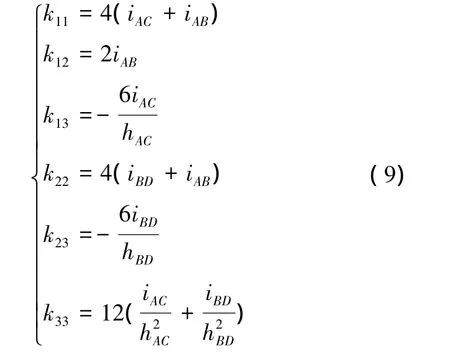
代入式(7)后可得

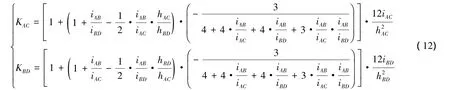
若定義

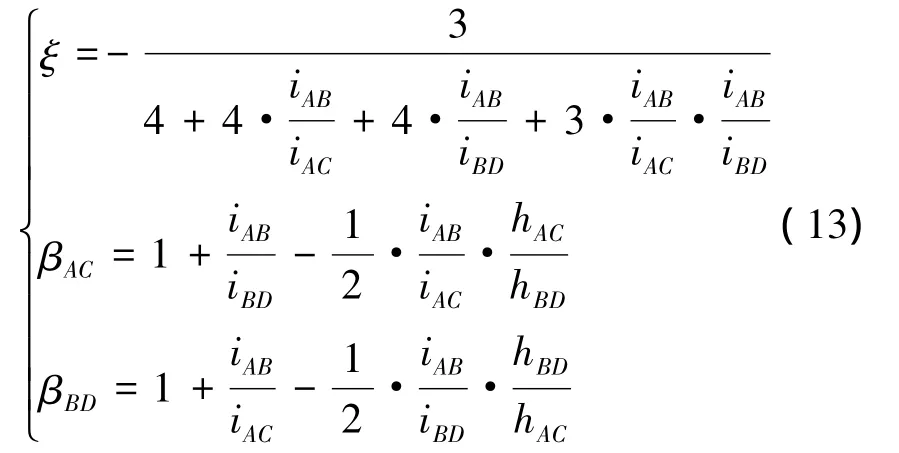
對于單層單跨不等高結構，最終長柱剛度Dl和短柱剛度Ds可表示為

式中:ib表示梁的線剛度，icl表示相對較長柱的線剛度，ics表示相對較短柱的線剛度，hcl表示相對較高柱的計算高度，hcs表示相對較短住的計算高度，Dl表示相對較長柱剛度，Ds表示相對較短柱剛度。系數ξ表示柱端節點轉角與柱底旋轉角的比例系數，反映了柱端節點轉角占柱旋轉角比例的大小;系數β表示柱旋轉能力系數，主要受相鄰梁柱線剛度比和自身與相鄰柱高度比影響，柱高度比越大β越小。系數α表示節點轉動和柱子旋轉能力影響系數，當達到相同的層側移，柱越高柱旋轉角越小(φ=Δ/h)對應的節點轉動相應減小，α則變大。也就是高柱的旋轉能力和節點轉動能力比短柱的小，所以長柱的αl比短柱的αs大，之所以長柱剛度比短柱小是因為截面剛度在D值中起主導作用。

2.2 單跨不等高柱側向剛度計算方法驗證

為驗證單跨不等高柱側向剛度計算方法的準確性及合理性，分別對第1節中的算例采用本文方法計算側向剛度及剪力。從表2計算結果對比中可以看出，雖然高度比在變化，本文方法計算剛度誤差變化很小，誤差基本在8%以內;剪力誤差隨著高度比變化更小，誤差基本在1%以內。對比表1和表2可以看出，采用本文方法相比Muto’s D值法計算結果更加接近精確解。從而說明本文提出的單跨不等高柱側向剛度計算精度較高，計算結果較準確。

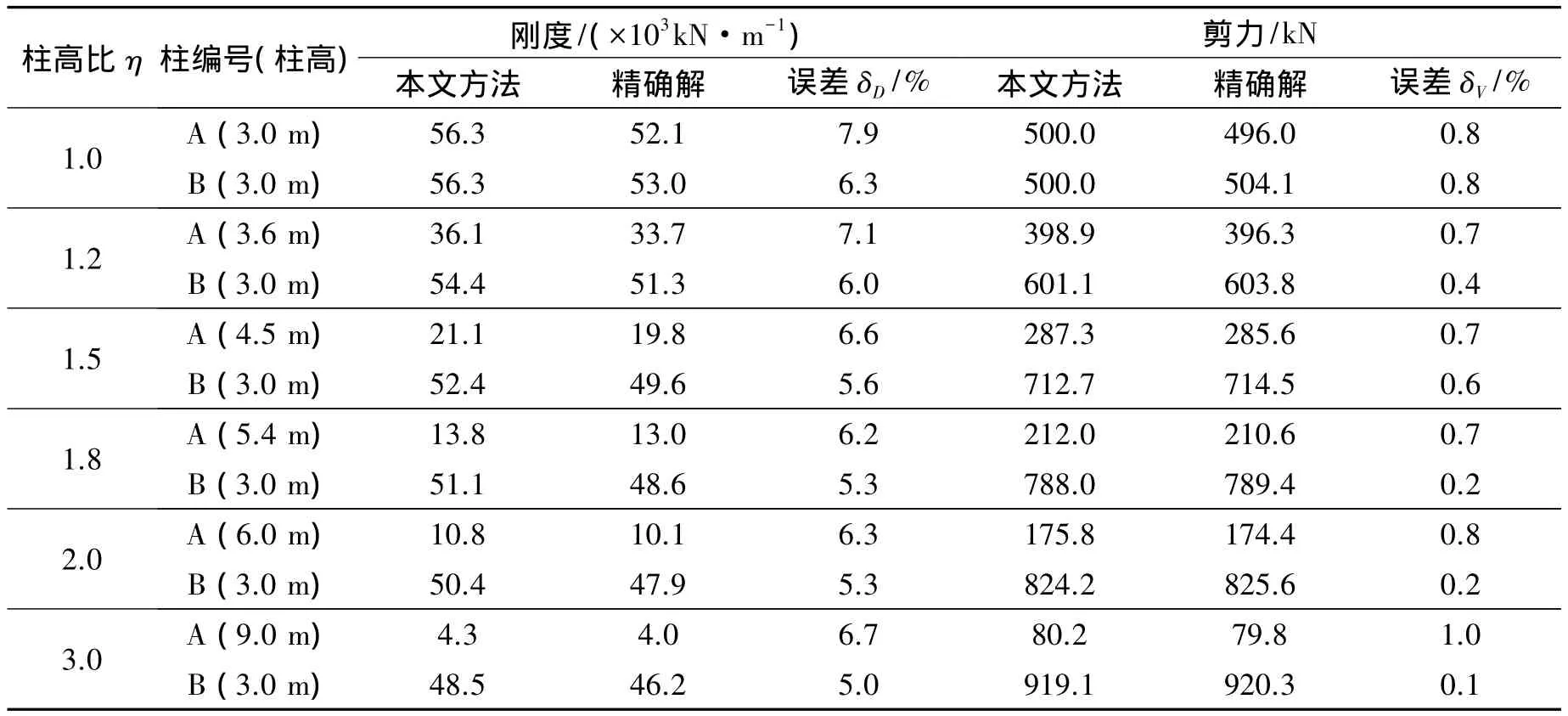
表2 計算誤差對比Table 2 The comparison of calculation error

2.3 多跨不等高柱側向剛度推導

多跨不等高框架可近似看成是多個單跨不等高框架并聯而成，如圖2所示，從分離體中可以看出仍然可按以上單跨不等高框架的推導，那么多跨不等高柱的剛度計算公式如下

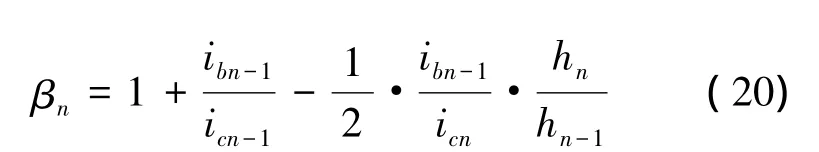
式中:ib表示梁的線剛度，icj表示計算柱的線剛度，icj+1表示相鄰較短柱線剛度，hcj表示計算柱高度，hcj+1表示相鄰較短柱計算高度，Dj表示計算柱剛度，ξj表示柱端節點轉角與柱底旋轉角的比例系數，βj表示柱旋轉能力系數，αj表示柱端節點轉動和柱子旋轉影響系數，其中最長柱子相對剛度較弱對于最長柱子α1需要再乘以0.85的修正系數。最終得到多跨不等高柱框架剛度計算公式，如表3。

圖2 多跨不等高柱框架模型Fig.2 The multi-span model with uneven ground column heights

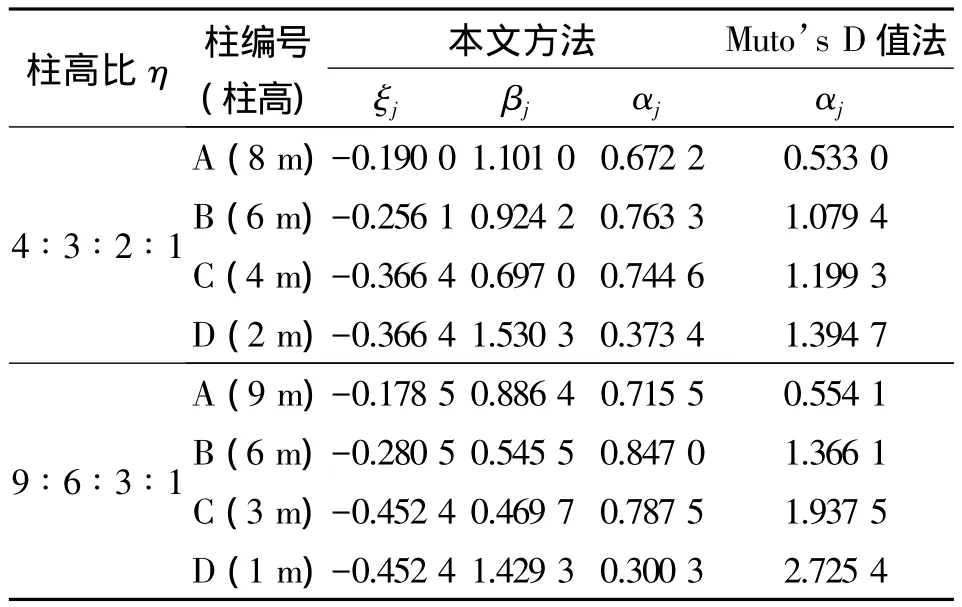
表3 剛度影響系數對比Table 3 The comparison of stiffness effect factor

2.4 多跨不等高柱側向剛度計算方法驗證

建立底層柱高比為4∶3∶2∶1和9∶6∶3∶1，從長到短柱依次編號為A、B、C、D，柱高比的變化就相當于山地的坡度變化。設計基本信息:跨度6 m，梁截面均為 250 mm×550 mm，柱截面均為550 mm×550 mm，左側頂點加水平集中力為1 000 kN。

從圖3中可以看出，隨坡高比的增加，采用本文方法計算剛度誤差在6%以內，剪力誤差基本也在7%以內，只有個別達到12.5%，但是其剪力相差僅有0.3 kN，本文方法與精確解吻合的較好。而Muto’s D值法計算結果誤差較大，尤其剛度計算結果明顯已失真。

從表3中看出D值法計算的αj值明顯小于本文修正后的αj值，這也反映出Muto’s D值法對柱端節點轉角及柱底旋轉角考慮不足。

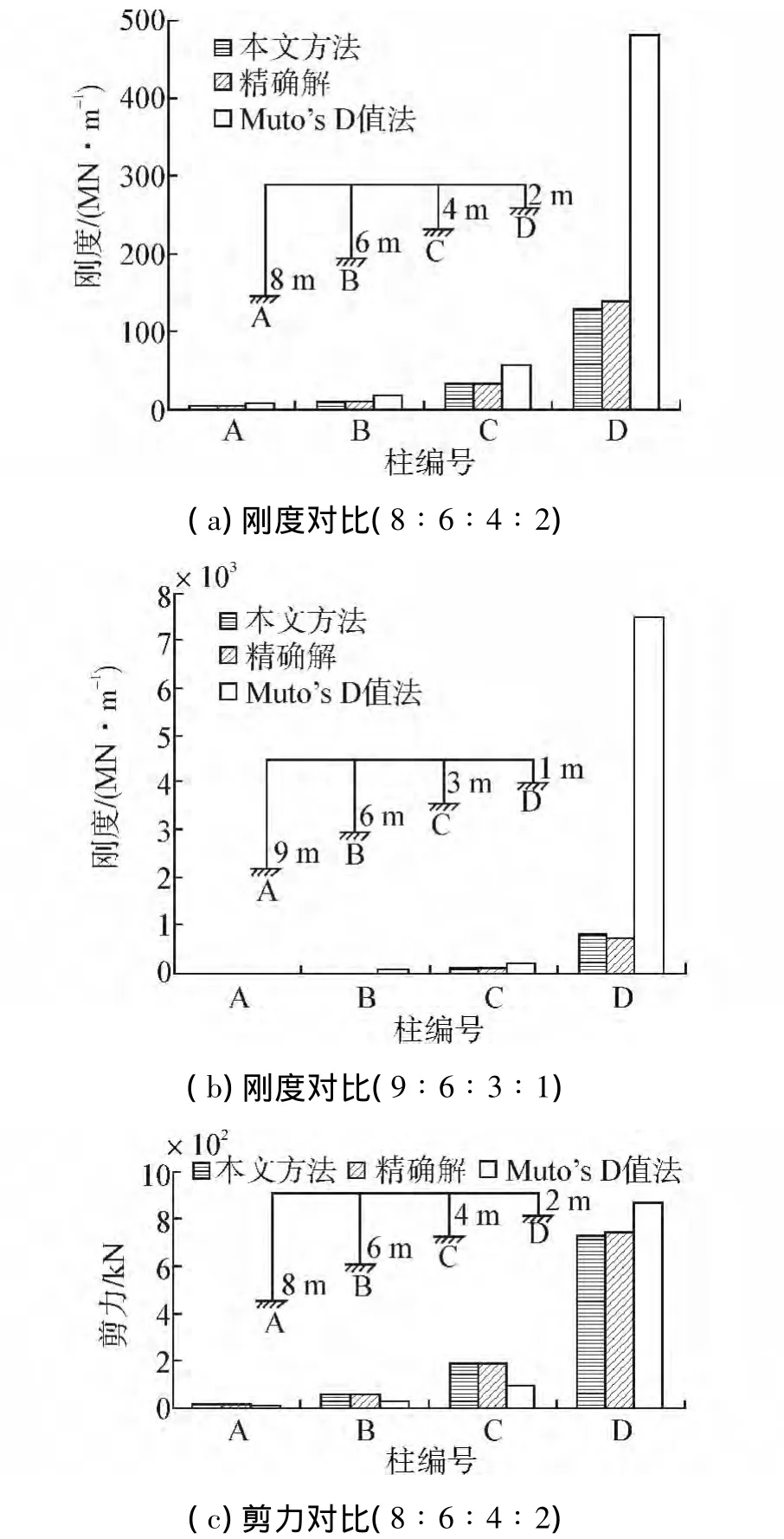
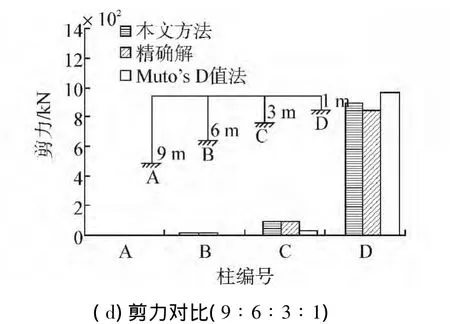
圖3 剛度和剪力對比圖Fig.3 The comparison of stiffness and shear forces

2.5 底部不等高柱框架結構側向剛度計算方法

對于多層多跨底部不等高柱框架結構中間層如圖4(a)柱剛度D可按下式計算:

其中

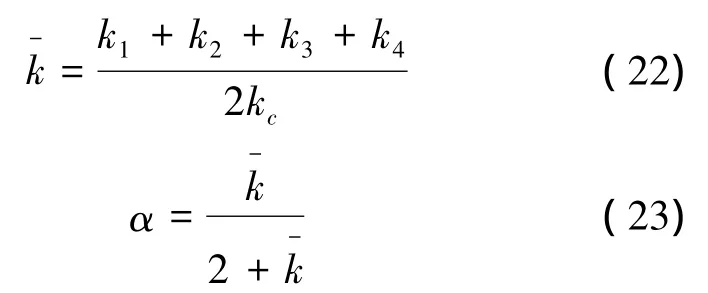
對于其底層如圖4(b)柱剛度Dj可按下式計算:

其中

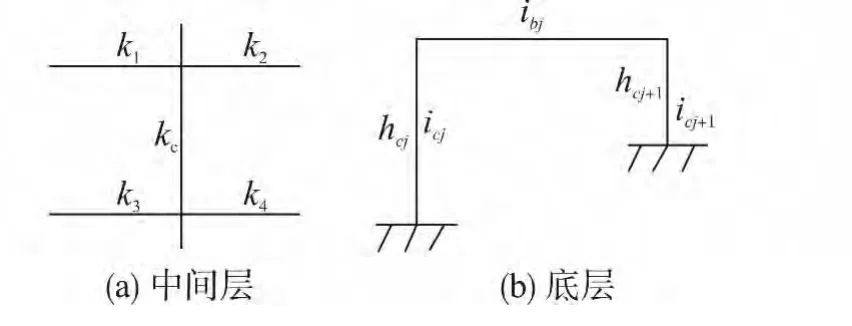
圖4 不同層Fig.4 Different floors

3 結論

本文通過力學推導，得到山地底部不等高柱框架結構的剛度計算方法，并得到以下結論:

1)采用已有的Muto＇s D值法計算底部不等高柱剛度和剪力時，發現隨著底層柱高度比的增加，無論剛度相對誤差還是剪力相對誤差都會逐漸增大。因此，Muto＇s D值法對計算底層不等高柱山地結構的內力已不適用。

2)通過力學推導，最終實現了在剛度修正系數中考慮柱端節點轉角和柱底旋轉角差異的影響，提出了單跨不等高框架側向剛度計算方法，并驗證了本文方法的準確性。

3)基于假設多跨不等高框架由多個單跨不等高框架并聯而成，從而在單跨不等高柱框架側向剛度計算方法的基礎上，得到多跨不等高柱框架剛度計算公式，通過驗證本文修正方法和精確解吻合較好。

4)對于多層多跨底層不等高框架結構，底層柱剛度可按本文方法計算，其余層可按普通框架結構D值法進行計算。本文研究完善了山地框架結構內力計算方法，為進一步控制山地建筑結構破壞模式的合理形成奠定理論基礎。

［1］王麗萍，李英民，鄭妮娜，等.5·12汶川地震典型山地建筑結構房屋震害調查［J］.西安建筑科技大學學報:自然科學版，2009，41(6):822-826.

WANG Liping，LI Yingmin，ZHENG Nina，et al.Seismic damage investigation on typical slope building in Wenchuan Earthquake［J］.Journal of Xi＇an University of Architecture＆Technology:Natural Science Edition，2009，41(6): 822-826.

［2］SINGH Y，GADE P，LANG D H，et al.Seismic behavior of buildings located on slopes－an analytical study and some observations from Sikkim Earthquake of September 18，2011［C］//Proceedings of the 15th World Conference on Earthquake Engineering.Lisbon Portugal，2012:250-256.

［3］LI Bing，KULKARNI S A.Seismic behavior of reinforced concrete exterior wide beam-column joints［J］.ASCE Journal of Structural Engineering，2010，136(1):26-36.

［4］LI Bing，GRACE H Y G.Seismic performance of strengthened reinforced concrete beam-column joints using FRP composites［J］.Journal of Structural Engineering，2009，135(10):1177-1190.

［5］WANG Liping，ZHONG Heping，HUANG Linqing.Analysis on seismic behavior of structures supported by foundations with different locations［C］//Proceedings of 4th International Conference on Manufacturing Science and Engineering.Dalian，2013:2729-2730.

［6］WANG Liping，ZHAO Yao.Comparative analysis of the influence of slope terrain on characteristics of horizontal and vertical ground motion response spectrum［C］//Proceedings of 2nd International Conference on Structures and Building Materials.Hangzhou，2012:2279-2284.

［7］JI Shuyan，GOETZ S，ZHAO Yao，et al.Analysis of factors influencing dynamic characteristics of building structures on slope［C］//Proceedings of 8th International Conference on Structure Dynamics.Belgium Leuven，2011:876-882.

［8］KUMAR S，PAUL D K.A simplified method for elastic seismic analysis of hill buildings［J］.Journal of Earthquake Engineering，1998，2(2):241-266.

［9］PAUL D K，KUMAR S.Stability analysis of slope with building loads［J］.Soil Dynamics and Earthquake Engineering，1997，16(6):395-405.

［10］BIRAJDAR B G，NALAWADE S S.Seismic analysis of buildings resting on sloping ground［C］//Proceedings of 13th World Conference on Earthquake Engineering.Vancouver，Canada，2004:1243-1248.

［11］馬千里，陸新征，葉列平.層屈服后剛度對地震響應離散性影響的研究［J］.工程力學，2008，25(7):133-141.

MA Qianli，LU Xinzheng，YE Lieping.Influence of the inter-story post-yield stiffness to the variance of seismic response［J］.Engineering Mechanics，2008，25(7):133-141.

［12］安偉光，趙維濤，嚴心池.不完整結構系統同時考慮強度和剛度的可靠性分析［J］.工程力學，2005，22(4): 58-61.

AN Weiguang，ZHAO Weitao，YAN Xinchi.Reliability analysis of imperfect structural systems considering strength and stiffness［J］.Engineering Mechanics，2005，22(4): 58-61.

［13］張川，王偉，陳劍鋒.水平側力下D值法在底層不等高框架內力計算中的應用［J］.世界地震工程，2002，18 (4):116-122.

ZHANG Chuan，WANG Wei，CHEN Jianfeng.Application of D-value method in structural analysis of frames with uneven height columns in the first story under lateral forces［J］.World Earthquake Engineering，2002，18(4):116-122.

［14］MUTO K.Seismic analysis of reinforced concrete buildings proceedings［C］//Proceedings of 1st World Conference on Earthquake Engineering.San Francisco，California，1956: 1-18.

［15］戎賢，張健新，李艷艷.提高異形柱框架節點抗震性能的試驗研究［J］.哈爾濱工程大學學報，2013，34(2):169-175.

RONG Xian，ZHANG Jianxin，LI Yanyan.Experimental research on seismic behavior of joints of specially shaped columns［J］.Journal of Harbin Engineering University，2013，34(2):169-175.

［16］于海豐，張文元.鉸接中心支撐鋼框架階形柱計算長度系數［J］.哈爾濱工程大學學報，2015，36(3):327-331.

YU Haifeng，ZHAGN Wenyuan.Effective length factos of stepped columns in the concentrically braced steel frame with pinned connections［J］.Journal of Harbin Engineering University，2015，36(3):327-331.

［17］陳樹華，欒偉偉.側向柱對預應力框架影響的等效彈簧模型［J］.哈爾濱工程大學學報，2003，24(6):686-689.

CHEN Shuhua，LUAN Weiwei.Equivalent spring model for the lateral frame columns for the influence of prestressed concrete frame structures［J］.Journal of Harbin Engineering University，2003，24(6):686-689.

［18］貢金鑫，于忠翰，張勤.基于pushover方法的結構抗震可靠度分析［J］.哈爾濱工程大學學報，2013，34(12): 1544-1550.

GONG Jinxing，YU Zhonghan，ZHANG Qin.Pushoverbased seismic reliability analysis of structures［J］.Journal of Harbin Engineering University，2013，34(12):1544-1550.