表面阻抗法測量水聲材料聲反射系數誤差分析

時勝國，王超，胡博

(1.哈爾濱工程大學水聲技術重點實驗室，黑龍江哈爾濱150001;2.哈爾濱工程大學水聲工程學院，黑龍江哈爾濱150001)

聲學材料聲反射系數是表征其聲學性能的重要參數，主要測量方法有阻抗管法、混響室法和自由場法等。阻抗管法［1-3］測量頻率范圍有限且僅能測量小樣品法向聲反射系數，無法真實反映實際應用中大樣材料的聲學特性;混響室法［4］僅能測量無規入射吸聲系數且穩定性欠佳。上述方法已得到了廣泛應用且有相應的測量標準。自由場法可以完成大樣品測量，能夠更加真實地反映材料在實際應用中的聲學特性。自由場方法會受到材料邊緣衍射效應的影響。為了規避邊緣衍射效應，人們提出了各種改進測量方法，如寬帶脈沖疊加法［5-6］、指向性聲源測試法［7］等。近年來，隨著矢量傳感器及其信號處理技術的發展，矢量傳感器已經應用于空氣聲學測量［8-10］領域。它可以同步、共點地測得聲場某點聲壓和質點振速信息，經過簡單計算可得到材料表面聲阻抗率，進而計算得到材料聲反射系數。與傳統雙聲壓傳聲器法［11-13］相比，矢量傳感器余弦接收指向性可以有效規避材料邊緣衍射效應，提高聲反射系數測量精度。

單矢量傳感器表面阻抗法的測量精度主要取決于測量原理、發射聲源和測量系統等參數。文獻［9-10］主要討論了聲源到樣本的距離、矢量傳感器到樣本距離和樣本尺寸大小等參數對測量結果的影響，但并未對表面阻抗法的測量誤差來源和測量不確定度進行理論分析。本文系統地分析了基于單矢量傳感器表面阻抗法的測量誤差來源和影響大小，主要從邊緣衍射效應和測量系統參數誤差兩方面進行理論分析，為實際工程應用提供指導性意見。

1 表面阻抗法測量理論分析

1.1 表面阻抗法測量原理

圖1中S為一點聲源，h為聲源到材料表面距離，r1為聲源到矢量傳感器距離，r2為虛源到矢量傳感器距離，d為矢量傳感器到材料表面距離，θ為聲波入射角。

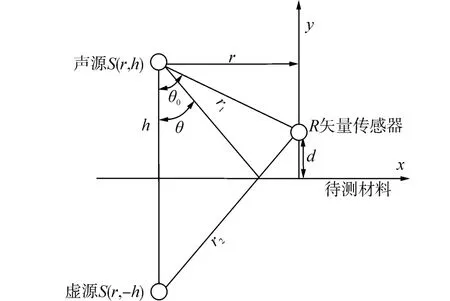
圖1 表面阻抗法測量模型示意圖Fig.1 Schematic diagram of the surface impedance method

直達波聲壓與法向質點振速為

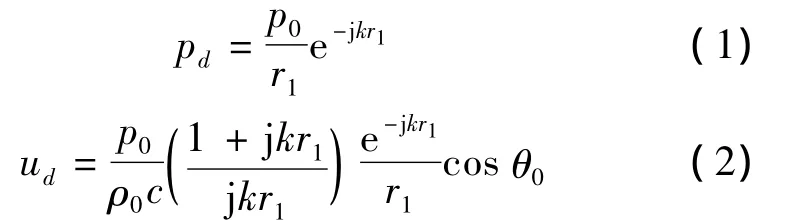
式中:k為波數，ρ0為介質密度，c為介質聲速，p0為聲源輻射聲壓幅值。材料聲壓反射系數為R，則反射波聲壓與法向質點振速為

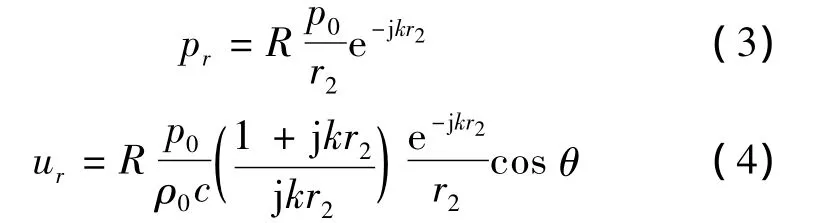
則材料表面聲阻抗率為

材料聲壓反射系數為

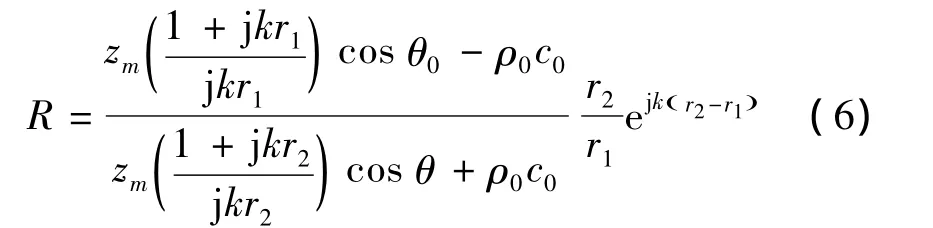
若kr1?1，則式(6)化簡為平面波表達式:

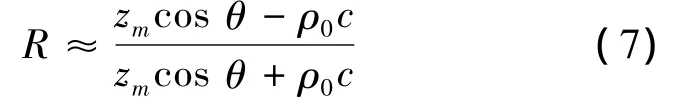
1.2 衍射效應計算模型

圖2中S為聲源，R為水聽器，A、B、C、D為矩形待測材料四邊中點，n為法向量，聲波以角度θ入射，材料四邊長均為L，聲源、水聽器到材料距離分別為h和d，θr1、θr2、θr3、θr4為四邊衍射角，θs1、θs2、θs3、θs4為入射聲波與材料表面夾角，β1、β2、β3、β4分別為入射波與材料邊緣夾角，Ped1、Ped2、Ped3和Ped4分別為四邊衍射波，A、B和Rs1、Rs2、Rs3、Rs4分別為接收點和聲源到材料四邊距離，球面波入射時邊緣衍射系數公式［14］為

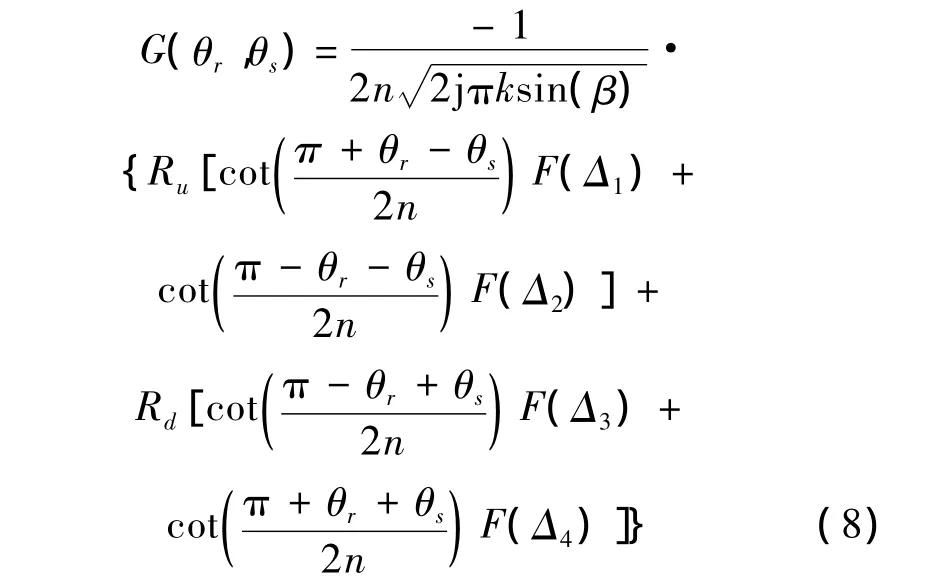
式中:矩形板取n=2，Ru、Rd分別為樣本兩側復反射系數，k為波數，F(*)為修正形式的菲涅爾積分，參數Δ1、Δ2、Δ3和Δ4為

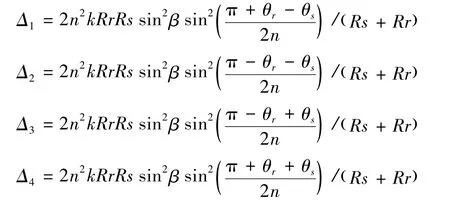
總衍射聲壓為

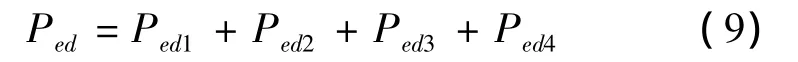
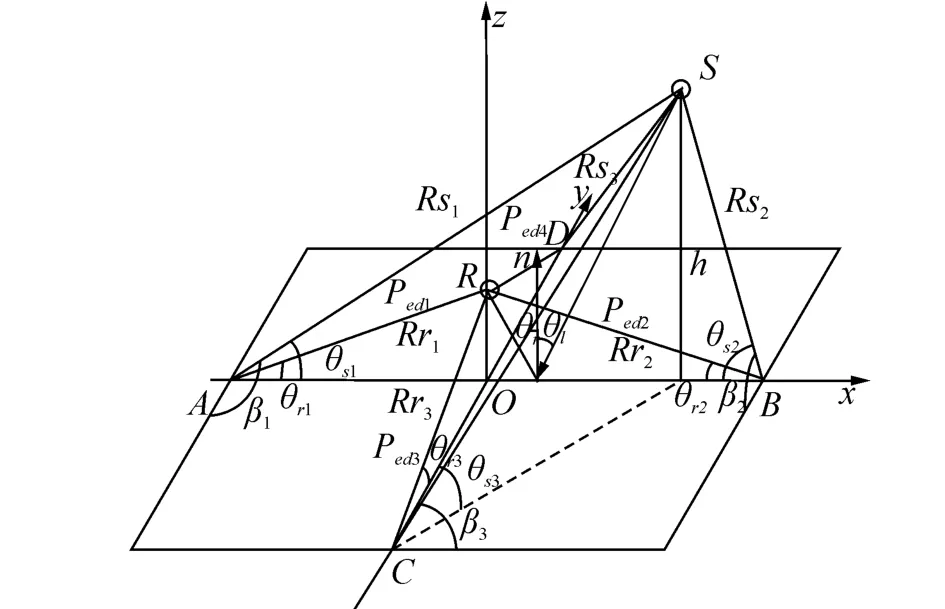
圖2 邊緣衍射模型示意圖Fig.2 Schematic diagram of the diffraction effect

1.3 測量不確定度分析

設間接測量量Y的估計值y由n個直接測量量x1，x2，…，xn的函數計算求得，即:

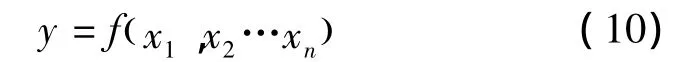
則測量結果y的合成標準不確定度為［15］

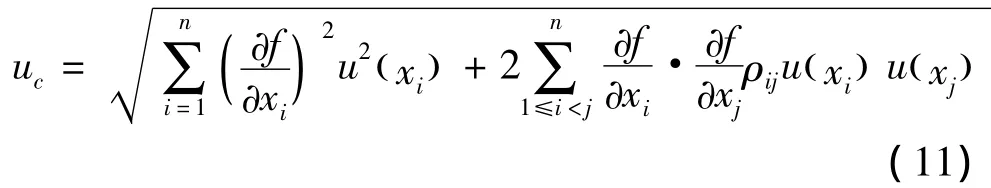
式中:?f/?xi為靈敏系數，ρij為任意2個不確定度的相關系數。單矢量傳感器表面阻抗法測量材料反射系數依賴于直接測量量H、d、θ和間接測量量阻抗率Zm的測量。Zm的測量相對合成不確定度為

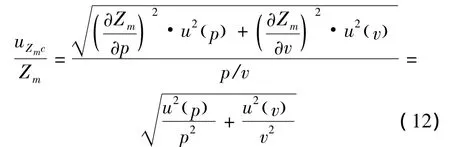
式中:u(p)/p與u(v)/v分別為聲壓和質點振速的相對不確定度，由矢量傳感器的性能決定。測量系統的測量不確定度及自由度為

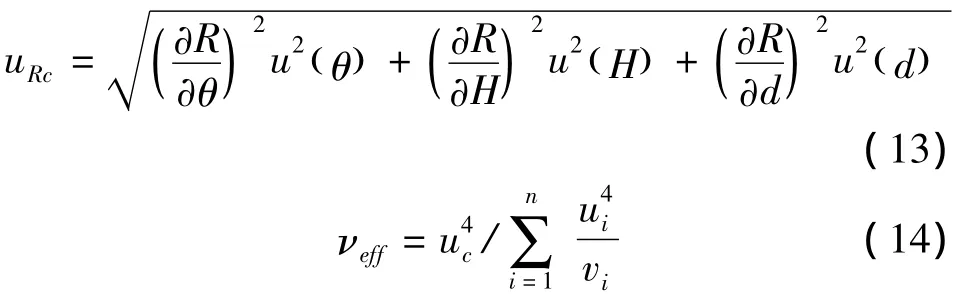
式中:u(*)為各個測量量的標準不確定度，vi為各標準不確定度分量ui的自由度。

取H、d和 θ的不度定度為 u(H)=0.3δH，u(d)=0.3δd和u(θ)=0.3δθ。設測量儀器分辨力為δH=0.01 m，δd=0.001 m，δθ=1°，當信號頻率和聲波入射角度分別為2 kHz和θ=30°時，uRc隨聲波入射角度和頻率變化規律如圖3所示。

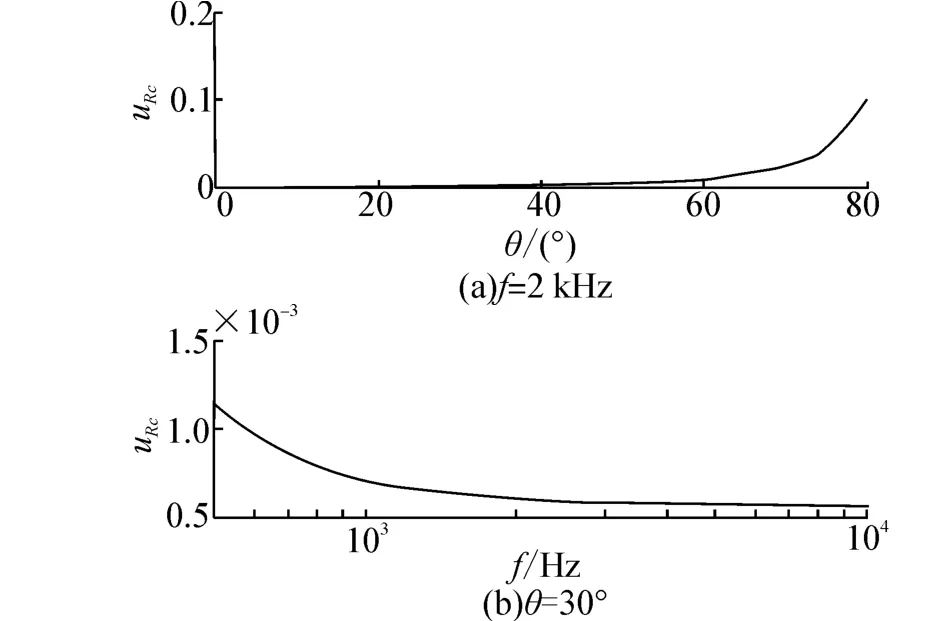
圖3 測量不確定度Fig.3 Uncertainty of the measurement

由圖3可知合成標準不確定度隨聲波入射角度變大而變大，隨頻率升高而減小。所以在低頻、大角度入射情況下應嚴格控制測量系統參數布放精度，減小測量系統參數誤差對測量結果的影響。

2 表面阻抗法測量誤差分析

本節仿真中，若無特殊說明，測量樣本均為鋁板，板厚0.006 m，幾何尺寸1 m×1 m，矢量傳感器到材料表面距離d=0.05 m，聲源到樣本距離H=5 m，信號頻率為500～10 kHz，頻率間隔為1/3倍頻程。

2.1 測量原理的誤差分析

仿真條件1:信噪比SNR=60 dB，聲波入射角θ=30°，聲源到樣本距離分別為H=2 m和H= 5 m，計算復反射系數模值隨頻率變化情況。

圖4給出了2個計算模型的計算結果，可見球面波計算模型精度高;平面波計算模型在低頻段誤差較大，但聲源越遠誤差越小。本文仿真均采用球面波測量模型。

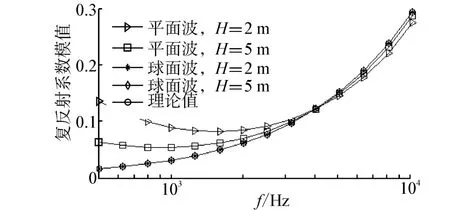
圖4 不同模型測量結果Fig.4 Measurement result of different models

2.2 材料邊緣衍射效應的影響分析

仿真條件2:采用雙聲壓水聽器法和單矢量傳感器表面阻抗法測量，聲波入射角θ分別為0°、30°、60°。

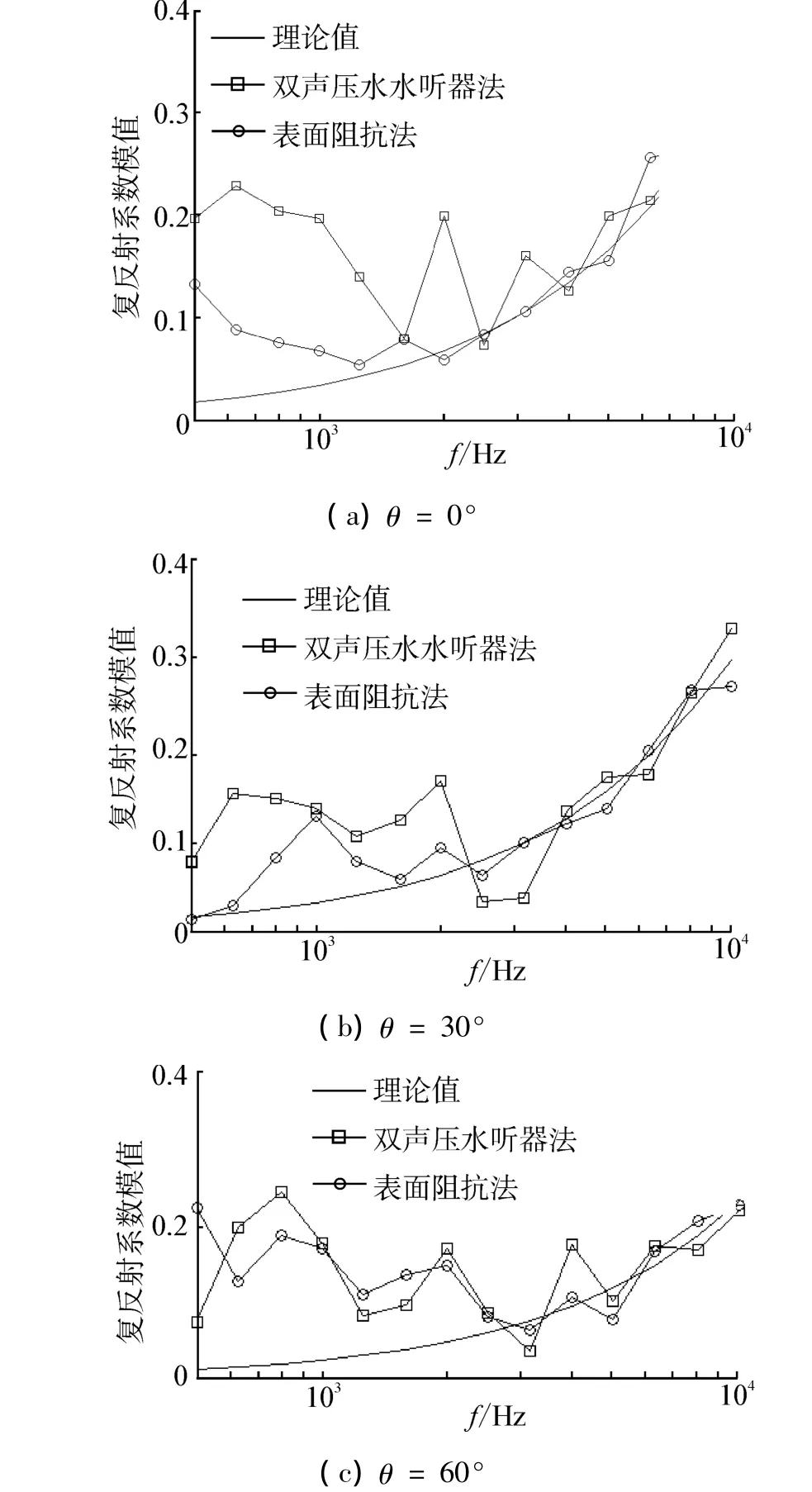
圖5 測量結果對比圖Fig.5 Contrast of the measurement results

圖5給出了單矢量傳感器表面阻抗法和雙聲壓水聽器法的測量結果。可見邊緣衍射效應對2kHz以下頻段影響較大，誤差隨聲波入射角度變大而變大，測量有效頻率下限隨聲波入射角度變大而升高;單矢量傳感器表面阻抗法性能優于雙聲壓水聽器法，小角度入射情況下測量更準確。為了抑制邊緣衍射，也可將矢量傳感器偏心放置，破壞樣本各邊衍射波的干涉，減小邊緣衍射影響。矢量傳感器偏離樣本中心5 cm布放，測量絕對誤差如圖6所示。

由圖6可知矢量傳感器偏心放置后最大誤差約為0.06，而同心放置測量結果最大誤差約為0.12。相較而言，除個別頻點外，偏心放置測量誤差較小。

邊緣衍射效應也可以通過增大樣本尺寸得到抑制。分析頻率為500 Hz，樣本邊長L=2m。測量誤差隨聲波入射角度變化如圖7所示。

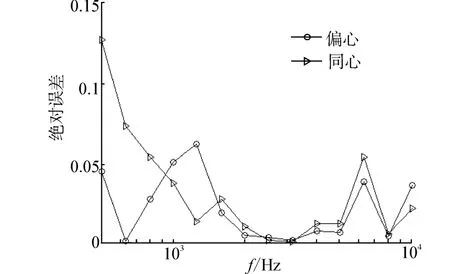
圖6 絕對誤差隨頻率變化曲線Fig.6 Absolute error versus frequency curve

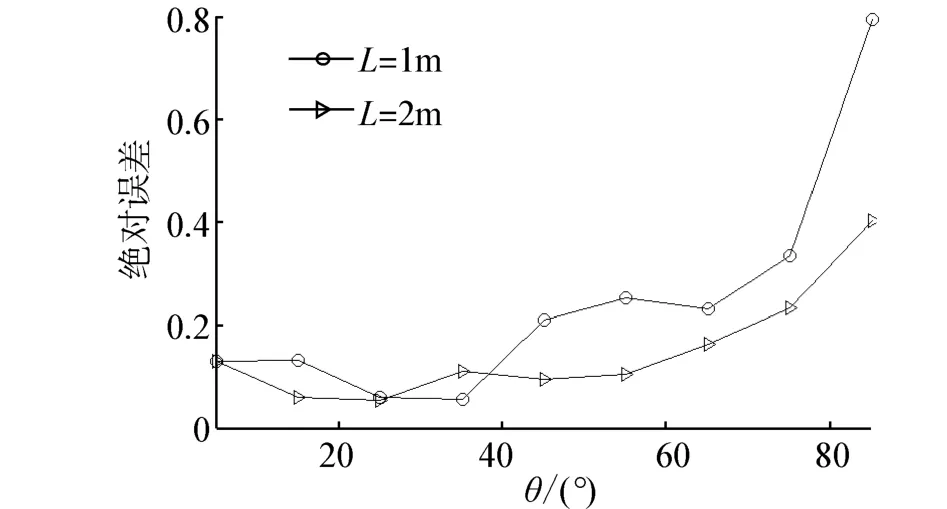
圖7 絕對誤差隨角度變化曲線Fig.7 Absolute error versus angle curve

由圖7可見增大樣本尺寸可以抑制衍射效應，測量絕對誤差隨入射角度變大而變大。

綜上仿真結果表明:矢量傳感器對抑制邊緣衍射效應起到了一定作用;測量時矢量傳感器應偏心放置或選取較大尺寸樣本。

2.3 測量系統誤差分析

2.3.1 發射信號信噪比影響分析

仿真條件3:信噪比 SNR分別為－10、10和30 dB，聲波入射角θ為0°。

由圖8可見當信噪比為－10 dB時測量結果符合理論變化趨勢，當信噪比達到10 dB時誤差可忽略。

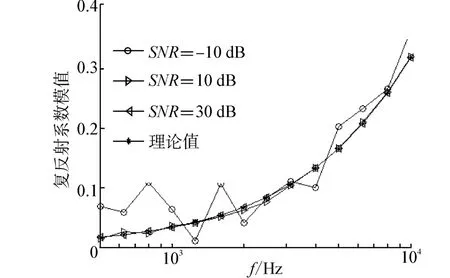
圖8 不同信噪比測量結果Fig.8 Measurement result in different SNR conditions

2.3.2 矢量傳感器各通道聲壓靈敏度誤差及相位一致性影響分析

矢量傳感器對表面阻抗法影響主要有聲壓、質點振速通道間相位一致性影響和靈敏度誤差影響。

仿真條件4:信噪比SNR=60 dB，聲波入射角度為0°，討論矢量傳感器聲壓、質點振速通道間相位差△Φpu分別為2°、3°、4°和5°時測量結果。

由圖9可見矢量傳感器聲壓、質點振速通道間相位一致性對測量結果影響較大。測量頻率小于6.3 kHz計算結果誤差較大;測量對矢量傳感器相位一致性敏感。圖中Φ為復反射系數R的相位。

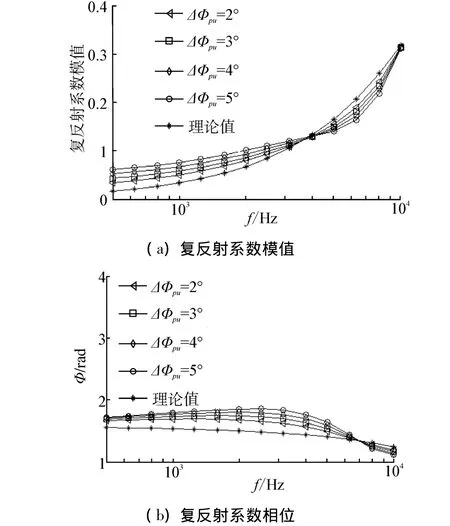
圖9 相位一致性影響Fig.9 The effect of the phase consistency

仿真條件5:信噪比SNR=60 dB，聲波0°入射，矢量傳感器聲壓與質點振速通道靈敏度誤差△Mp與△Mu分別為1、2和3 dB時測量結果。如圖10所示。

由圖10可見矢量傳感器各通道聲壓靈敏度誤差對測量結果影響較大;當聲壓通道或質點振速通道聲壓靈敏度存在2 dB誤差時模值測量失效;相位測量對矢量傳感器靈敏度誤差敏感，靈敏度存在1 dB誤差時測量失效。

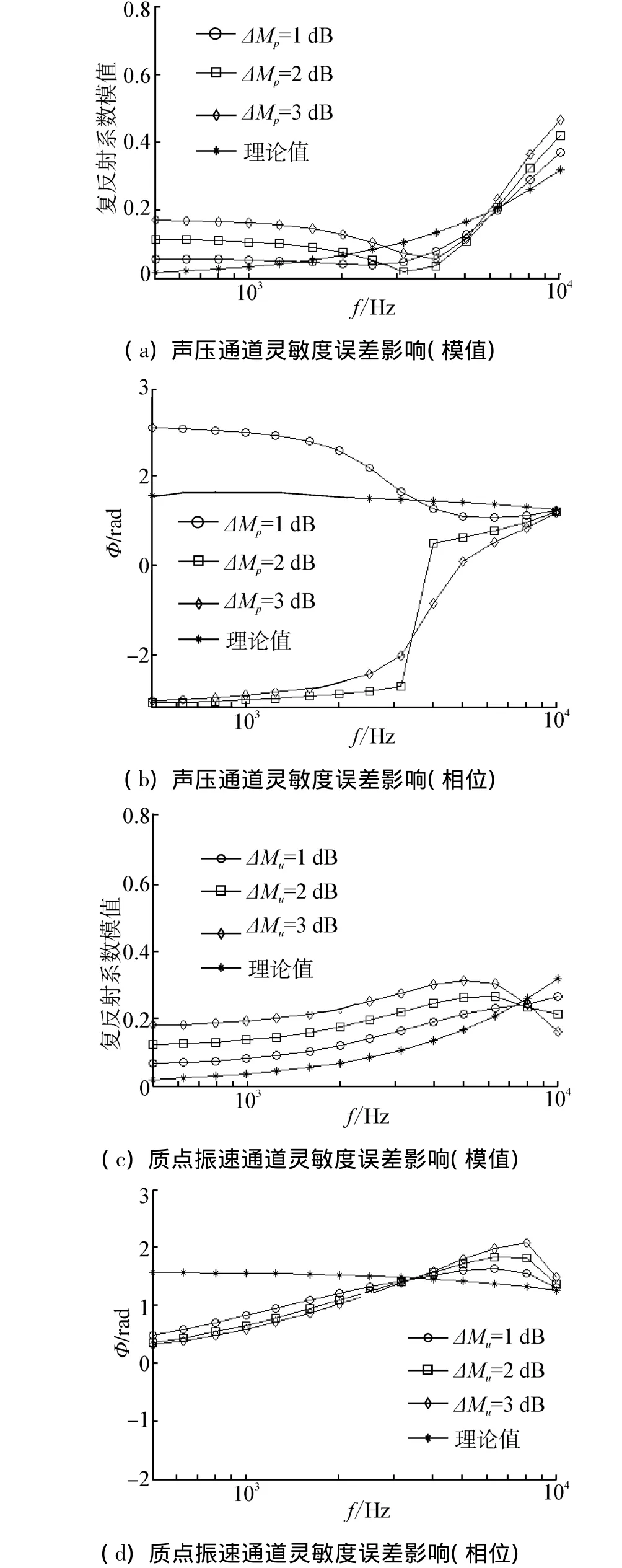
圖10 測量結果對比圖Fig.10 Contrast of the measurement results

測量時應首先對矢量傳感器進行靈敏度校準。靈敏度校準采用比較法校準。另外，應對測得的阻抗進行修正，聲源為點源時可得矢量傳感器處波阻抗Z0，實際測得的波阻抗為Zm，則修正因子為

2.3.3 測量系統布放誤差影響分析

仿真條件6:矢量傳感器到樣本距離d分別為0.05、0.1、0.15和0.2 m，信噪比SNR=60 dB，H布放存在1%誤差。以聲波0°入射和500 Hz時測量為例。

圖11給出了H布放不準確引起的相對誤差變化規律，可見在法向入射時最大相對誤差約為2.7%，在500 Hz時測量最大相對誤差約為5.2%。復反射系數測量在低頻、大角度入射時易受其影響，此時應控制聲源布放精度減少測量誤差。

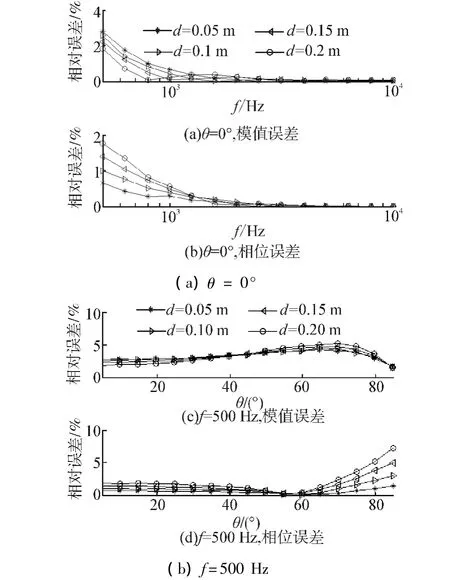
圖11 相位一致性影響Fig.11 The effect of the phase consistency

仿真條件7:信噪比SNR=60 dB，聲源到樣本距離H=2、3、4和5 m，d布放存在10%誤差。

由圖12可見聲源距離越遠誤差越小;聲波法向入射時，模值測量最大相對誤差小于1.5%;頻率為500 Hz時，入射角度大于40°測量相對誤差變大。復反射系數相位測量誤差隨頻率、入射角度變大而升高，且對矢量傳感器布放的誤差較為敏感。

仿真條件8:信噪比SNR=60 dB，若樣本在旋轉時存在0.2°角度誤差，測量誤差如圖13所示。

由圖13可見，模值測量相對誤差不超過0.4%，相位測量相對誤差不超過0.2%，可見表面阻抗法對θ不準確不敏感。

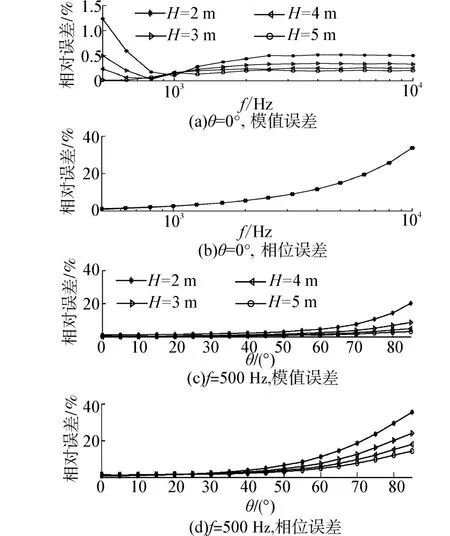
圖12 d布放引起的相對誤差Fig.12 The relative error caused by d

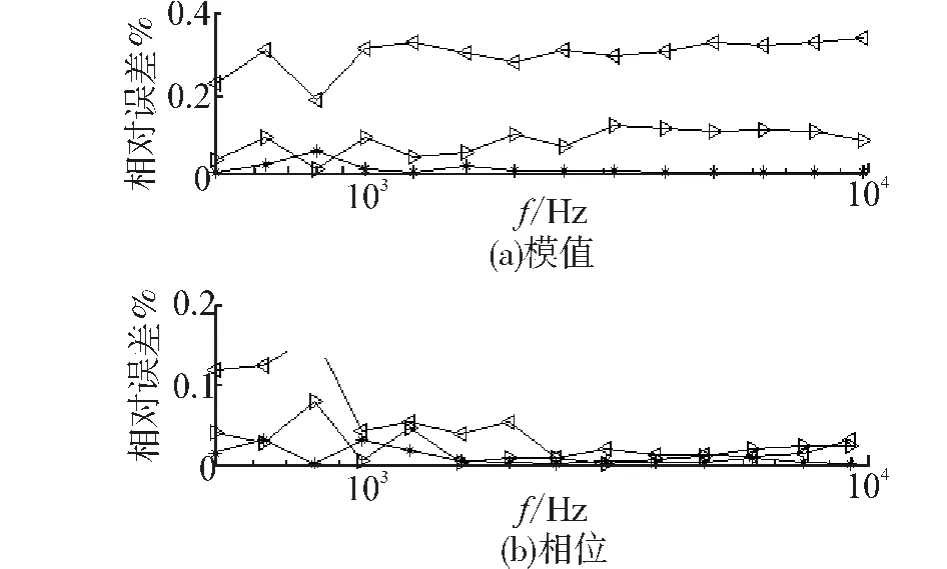
圖13 θ旋轉引起的相對誤差Fig.13 The relative error caused by pivoting θ

綜上仿真結果表明:單矢量傳感器表面阻抗法在低頻大角度入射時測量精度易受系統參數誤差的影響;矢量傳感器靈敏度誤差和相位一致性對測量結果影響最大，測量時可應用式(15)對阻抗進行修正。另外，在低頻、大角度入射時更應盡量控制系統布放準確性以保證測量結果精度。

3 結論

本文系統地分析了單矢量傳感器表面阻抗法的誤差來源，分析了材料邊緣衍射效應對測量結果的影響;同時，分析了測量計算模型精度、測量環境和測量系統參數誤差的影響。對比仿真計算結果得到以下結論:

1)球面波計算模型精度較高;平面波計算模型在低頻、大角度入射情況下誤差較大，測量時聲源布放應滿足遠場條件。

2)矢量傳感器對抑制邊緣衍射效應起到了一定作用，其測量性能優于雙聲壓水聽器法;邊緣衍射效應在低頻、大角度入射情況下影響較大;另外，為了規避材料邊緣衍射效應，矢量傳感器布放應適當偏離樣本中心位置。

3)單矢量傳感器表面阻抗法對測量環境信噪比的要求較低，信噪比在10 dB以上即可得到滿意的測量結果;但對矢量傳感器相位一致性和靈敏度誤差敏感，在實際測量時應利用修正因子CF對測量得到的表面聲阻抗率進行修正，再計算材料的聲反射系數。

4)總的來說，在低頻、大角度入射時表面阻抗法對測量系統H和d參數誤差較敏感，對θ參數誤差不敏感;測量時聲源應盡量遠離待測樣本，矢量傳感器應盡量靠近樣本;在低頻、大角度入射時更應注意控制系統參數誤差，提高測量精度。

［1］龐業珍.基于傳遞函數的吸聲隔聲測量方法與應用研究［D］.大連:大連理工大學，2005:17-20.

PANG Yazhen.Methods and applications of sound absorption and insulation measurement based on the transfer functions［D］.Dalian:Dalian University of Technology，2005: 17-20.

［2］羅馬奇，李水，易燕，等.水聲材料低頻聲性能行波管測量系統的改進及實驗［J］.聲學技術，2009，28(4):59-62.

LUO Maqi，LI Shui，YI Yan，et al.Improvement and experiments of traveling wave tube measurement system for lowfrequency properties of underwater acoustic materials［J］.Technical Acoustics，2009，28(4):59-62.

［3］曲波，朱蓓麗.駐波管中隔聲量的四傳感器測量法［J］.噪聲與振動控制，2002(6):44-46.

QU Bo，ZHU Beili.Four-microphone method of sound transmission in the standing wave tube［J］.Noise and Vibration Control，2002(6):44-46.

［4］侯宏，徐士化.近代現場吸聲測量技術［J］.聲學技術，2007，26(6):1209-1213.

HOU Hong，XU Shihua.A review of modern in-situ sound absorption measurement techniques［J］.Technical Acoustics，2007，26(6):1209-1213.

［5］李水，繆榮興.水聲材料性能的自由場寬帶壓縮脈沖疊加法測量［J］.聲學學報，2000，25(3):248-253.

LI Shui，MIAO Rongxing.Measurements for the properties of underwater acoustic materials by broadband compressed pulse superposition method［J］.Acta Acustica，2000，25 (3):248-253.

［6］李水，羅馬奇，易燕，等.水聲材料構件聲學特性自由場寬帶測量裝置［J］.聲學學報，2011，36(5):534-541.

LI Shui，LUO Maqi，YI Yan，et al.The broadband measurement facility for acoustic characteristics of underwater acoustic materials in free fields［J］.Acta Acustica，2011，36 (5):534-541.

［7］姬培鋒，楊軍，李曉東.基于指向性聲源的吸聲系數測量［C］//全國聲學學術會議論文集.廈門，中國，2006: 495-496.

JI Peifeng，YANG Jun，LI Xiaodong.Sound-absorption coefficient measurement based on the directional speaker［C］//Symposium of Acoustical Society of China.Xiamen，China，2006:495-496.

［8］LANOYE R，DE BREE H E，LAURIKS W，et al.A practical device to determine the reflection coefficient of acoustic materials in-situ based on a Microflown and microphone sensor［J］.ISMA，2004，1(8):2665-2675.

［9］LANOYE R，VERMEIR G，LAURIKS W，et al.Measuring the free field acoustic impedance and absorption coefficient of sound absorbing materials with a combined particle velocity-pressure sensor［J］.The Journal of the Acoustical Society of America，2006，119(5):2826-2831.

［10］HIROSAWA K，TAKASHIMA K，NAKAGAWA H，et al.Comparison of three measurement techniques for the normal absorption coefficient of sound absorbing materials in the free field［J］.The Journal of the Acoustical Society of A-merica，2009，126(6):3020-3027.

［11］陳克安，曾向陽.雙傳聲器法測量斜入射吸聲系數研究［J］應用聲學，1999，18(4):28-32.

CHEN Ke'an，ZENG Xiangyang.A study on the measurement of sound absorption coefficient at oblique incidence by the use of two-microphone technique［J］.Applied Acoustic，1999，18(4):28-32.

［12］TAKAHASHI Y，OTSURU T，TOMIKU R.In situ measurements of surface impedance and absorption coefficients of porous materials using two microphones and ambient noise［J］.Applied Acoustics，2005，66(7):845-865.

［13］ALLARD J F，SIEBEN B.Measurements of acoustic impedance in a free field with two microphones and a spectrum analyzer［J］.The Journal of the Acoustical Society of America，1985，77(4):1617-1618.

［14］LIU Yansen，SHENG Meiping，WANG Meiyan，et al.Modeling and calculating on the diffraction acoustic field originated from underwater flat structure with finite impedance surface［J］.Journal of Ship Mechanics，2009，13 (6):1002-1012.

［15］吳石林，張玘.誤差分析與數據處理［M］.北京:清華大學出版社，2010:175-193.